第 2 章 马尔可夫决策过程

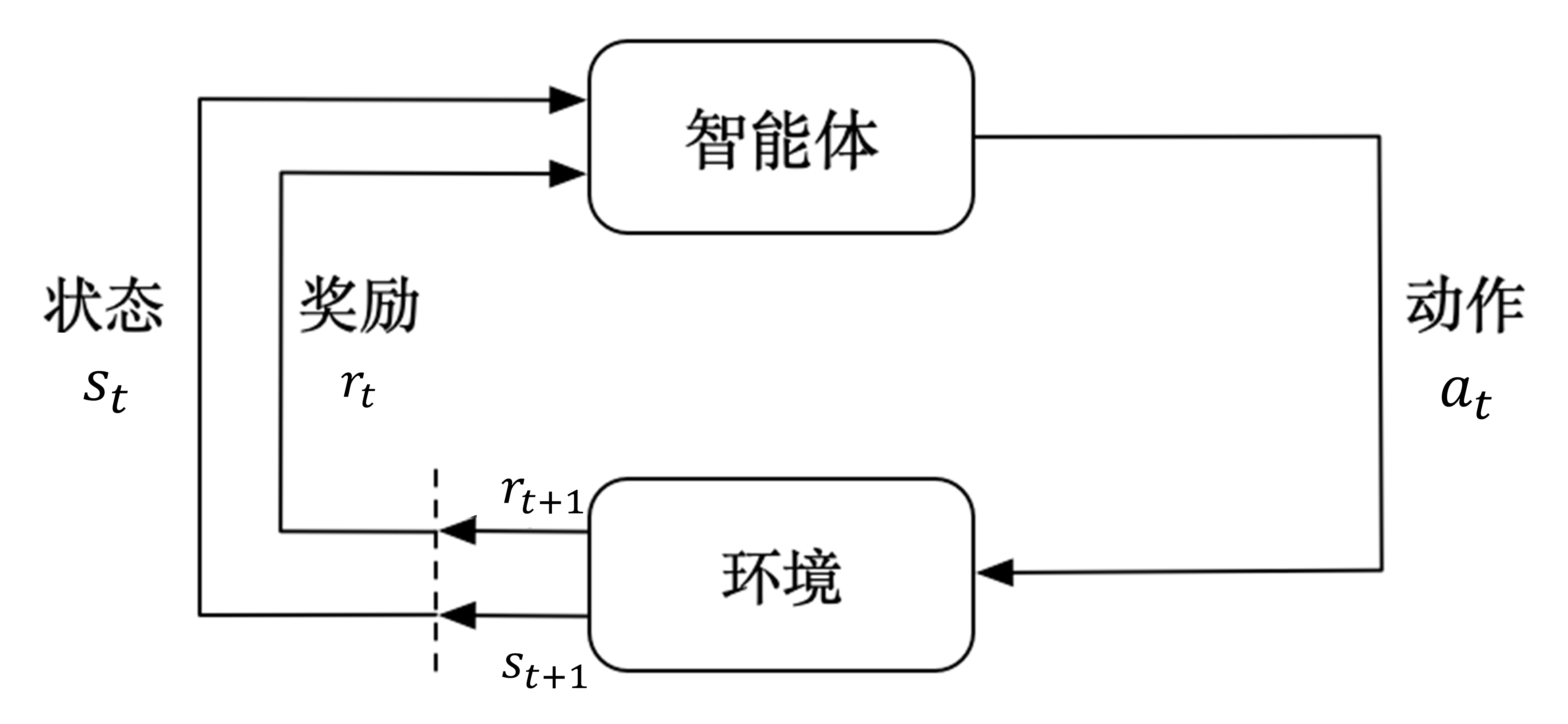
图 2.1 介绍了强化学习里面智能体与环境之间的交互，智能体得到环境的状态后，它会采取动作，并把这个采取的动作返还给环境。环境得到智能体的动作后，它会进入下一个状态，把下一个状态传给智能体。在强化学习中，智能体与环境就是这样进行交互的，这个交互过程可以通过马尔可夫决策过程来表示，所以马尔可夫决策过程是强化学习的基本框架。

本章将介绍马尔可夫决策过程。在介绍马尔可夫决策过程之前，我们先介绍它的简化版本：马尔可夫过程（Markov process，MP）以及马尔可夫奖励过程（Markov reward process，MRP）。通过与这两种过程的比较，我们可以更容易理解马尔可夫决策过程。其次，我们会介绍马尔可夫决策过程中的策略评估（policy evaluation），就是当给定决策后，我们怎么去计算它的价值函数。最后，我们会介绍马尔可夫决策过程的控制，具体有策略迭代（policy iteration） 和 价值迭代（value iteration） 两种算法。在马尔可夫决策过程中，它的环境是全部可观测的。但是很多时候环境里面有些量是不可观测的，但是这个部分观测的问题也可以转换成马尔可夫决策过程的问题。

2.1 马尔可夫过程

2.1.1 马尔可夫性质

在随机过程中，马尔可夫性质（Markov property） 是指一个随机过程在给定现在状态及所有过去状态情况下，其未来状态的条件概率分布仅依赖于当前状态。以离散随机过程为例，假设随机变量 $X_0,X_1,\cdots,X_T$构成一个随机过程。这些随机变量的所有可能取值的集合被称为状态空间（state space）。如果 $X_{t+1}$ 对于过去状态的条件概率分布仅是 $X_t$ 的一个函数，则

$$p\left(X_{t+1}=x_{t+1} \mid X_{0:t}=x_{0: t}\right)=p\left(X_{t+1}=x_{t+1} \mid X_{t}=x_{t}\right)$$

其中， $X_{0:t}$ 表示变量集合 $X_{0}, X_{1}, \cdots, X_{t}$， $x_{0: t}$ 为在状态空间中的状态序列 $x_{0}, x_{1}, \cdots, x_{t}$。马尔可夫性质也可以描述为给定当前状态时，将来的状态与过去状态是条件独立的。如果某一个过程满足马尔可夫性质，那么未来的转移与过去的是独立的，它只取决于现在。马尔可夫性质是所有马尔可夫过程的基础。

2.1.2 马尔可夫链

马尔可夫过程是一组具有马尔可夫性质的随机变量序列 $s_1,\cdots,s_t$，其中下一个时刻的状态 $s_{t+1}$只取决于当前状态 $s_t$。我们设状态的历史为 $h_{t}=\left\{s_{1}, s_{2}, s_{3}, \ldots, s_{t}\right\}$（ $h_t$ 包含了之前的所有状态），则马尔可夫过程满足条件：

$$p\left(s_{t+1} \mid s_{t}\right) =p\left(s_{t+1} \mid h_{t}\right) \tag{2.1}$$

从当前 $s_t$ 转移到 $s_{t+1}$，它是直接就等于它之前所有的状态转移到 $s_{t+1}$。

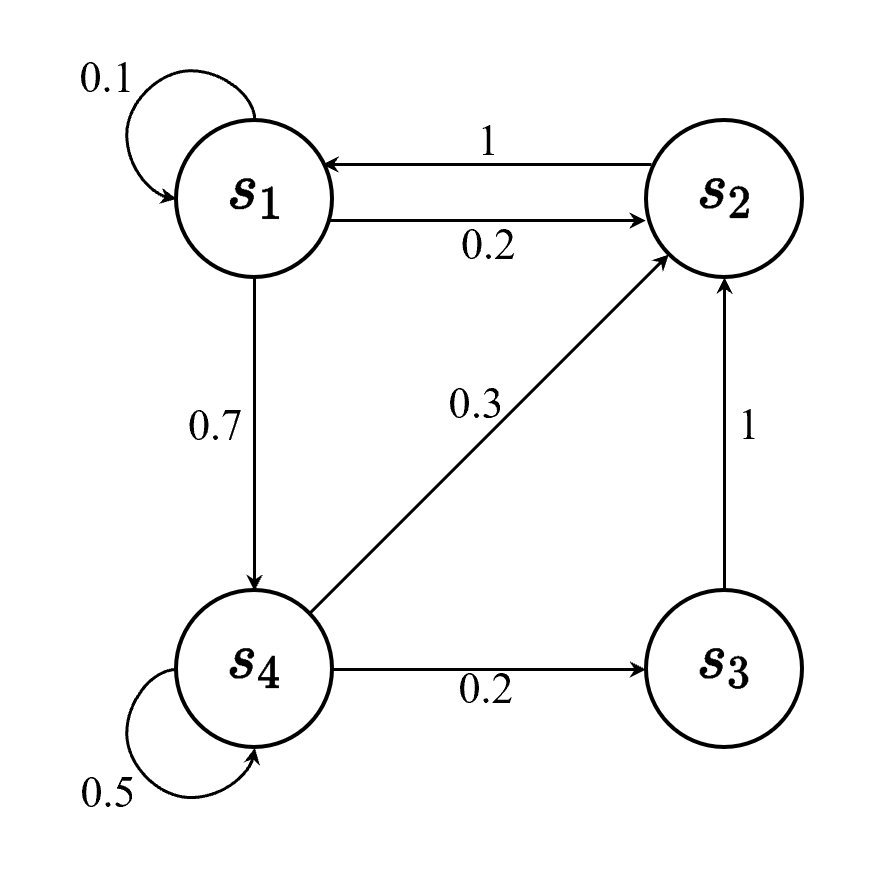
离散时间的马尔可夫过程也称为马尔可夫链（Markov chain）。马尔可夫链是最简单的马尔可夫过程，其状态是有限的。例如，图 2.2 里面有4个状态，这4个状态在 $s_1,s_2,s_3,s_4$ 之间互相转移。比如从 $s_1$ 开始， $s_1$ 有 0.1 的概率继续存留在 $s_1$ 状态，有 0.2 的概率转移到 $s_2$，有 0.7 的概率转移到 $s_4$ 。如果 $s_4$ 是我们的当前状态，它有 0.3 的概率转移到 $s_2$，有 0.2 的概率转移到 $s_3$，有 0.5 的概率留在当前状态。

我们可以用状态转移矩阵（state transition matrix） $\boldsymbol{P}$ 来描述状态转移 $p\left(s_{t+1}=s^{\prime} \mid s_{t}=s\right)$：

$$\boldsymbol{P}=\left(\begin{array}{cccc} p\left(s_{1} \mid s_{1}\right) & p\left(s_{2} \mid s_{1}\right) & \ldots & p\left(s_{N} \mid s_{1}\right) \\ p\left(s_{1} \mid s_{2}\right) & p\left(s_{2} \mid s_{2}\right) & \ldots & p\left(s_{N} \mid s_{2}\right) \\ \vdots & \vdots & \ddots & \vdots \\ p\left(s_{1} \mid s_{N}\right) & p\left(s_{2} \mid s_{N}\right) & \ldots & p\left(s_{N} \mid s_{N}\right) \end{array}\right)$$

状态转移矩阵类似于条件概率（conditional probability），它表示当我们知道当前我们在状态 $s_t$ 时，到达下面所有状态的概率。所以它的每一行描述的是从一个节点到达所有其他节点的概率。

2.1.3 马尔可夫过程的例子

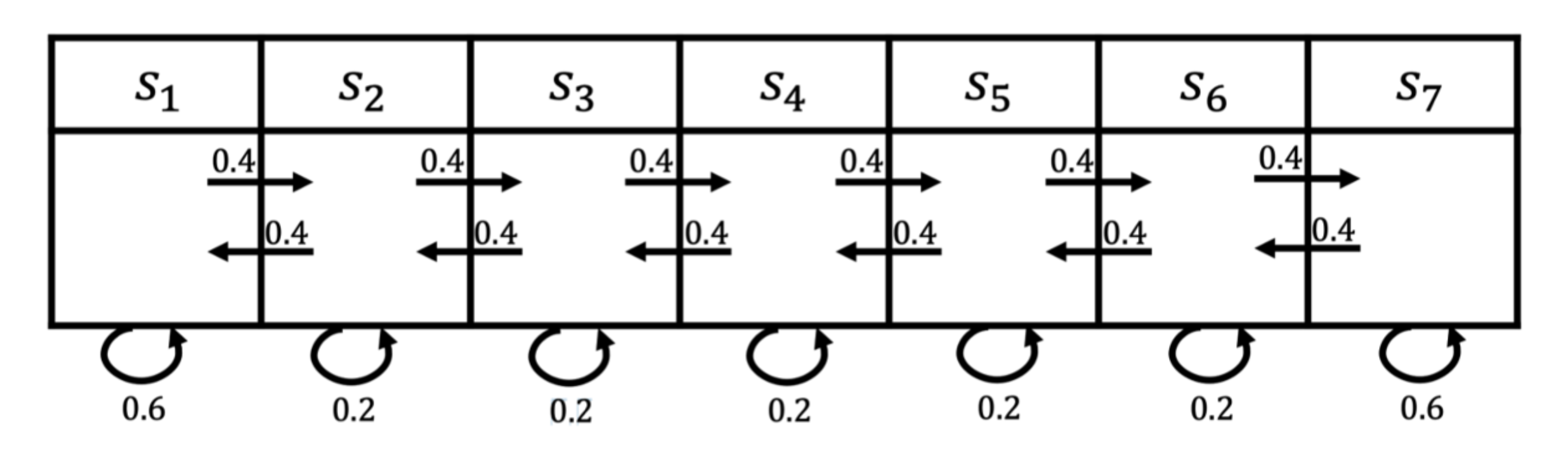
图 2.2 所示为一个马尔可夫过程的例子，这里有七个状态。比如从 $s_1$ 开始，它有0.4的概率到 $s_2$ ，有 0.6 的概率留在当前的状态。 $s_2$ 有 0.4 的概率到 $s_1$，有 0.4 的概率到 $s_3$ ，另外有 0.2 的概率留在当前状态。所以给定状态转移的马尔可夫链后，我们可以对这个链进行采样，这样就会得到一串轨迹。例如，假设我们从状态 $s_3$ 开始，可以得到3个轨迹：

• $s_3, s_4, s_5, s_6, s_6$；
• $s_3, s_2, s_3, s_2, s_1$；
• $s_3, s_4, s_4, s_5, s_5$。

通过对状态的采样，我们可以生成很多这样的轨迹。

2.2 马尔可夫奖励过程

马尔可夫奖励过程（Markov reward process, MRP）是马尔可夫链加上奖励函数。在马尔可夫奖励过程中，状态转移矩阵和状态都与马尔可夫链一样，只是多了奖励函数（reward function）。奖励函数 $R$ 是一个期望，表示当我们到达某一个状态的时候，可以获得多大的奖励。这里另外定义了折扣因子 $\gamma$ 。如果状态数是有限的，那么 $R$ 可以是一个向量。