@TOC

简介

Hello！
非常感谢您阅读海轰的文章，倘若文中有错误的地方，欢迎您指出～
 
ଘ(੭ˊᵕˋ)੭
昵称：海轰
标签：程序猿｜C++选手｜学生
简介：因C语言结识编程，随后转入计算机专业，获得过国家奖学金，有幸在竞赛中拿过一些国奖、省奖…已保研
学习经验：扎实基础 + 多做笔记 + 多敲代码 + 多思考 + 学好英语！
 
唯有努力💪
 
本文仅记录自己感兴趣的内容

Abstract

相邻顶点度的双变量分布，度度分布，是定义相邻顶点度之间的统计依赖关系的重要网络特征。

我们展示了稀疏非齐次随机相交图的渐近度-度分布，并讨论了它与图的聚类和幂律性质的关系。

1 Introduction

相邻顶点度数之间的相关性会影响许多网络属性，包括组件结构、流行病传播、随机游走性能、网络鲁棒性等，参见 [2]、[8]、[12]、[18]、[19] 和参考资料其中。相关性由度数分布定义，即随机选择的边缘的端点度数的二元分布。在本文中，我们对具有可调幂律度分布和聚类系数的隶属网络的数学上易处理的随机图模型中的度度分布进行了分析研究。我们的研究是出于对追踪幂律网络中度数分布和聚类属性之间关系的兴趣。网络。

隶属网络和随机相交图。 附属网络通过使用一组辅助属性来定义参与者之间的邻接关系。令 V 表示参与者（网络的节点）集，W 表示辅助属性集。每个参与者 v ∈ V 都被规定了一个属性集合 Sv ⊂ W 并且两个参与者 u, v ∈ V 如果它们共享一些共同的属性，则在网络中被声明为相邻。例如，可以将 W 的元素解释为权重，并在共享属性的总权重高于某个阈值时声明两个参与者相邻。

这里我们考虑最简单的情况，当 u, v ∈ V 共享至少一个共同属性时，它们被称为相邻，即 Su ∩ Sv 6 = ∅。真实隶属关系网络的两个流行例子是电影演员网络，如果两个演员在同一部电影中演出，则被宣布为相邻；合作网络，如果两名科学家共同撰写了出版物，则被宣布为相邻。

通过将属性集合随机指定给参与者，可以获得大型隶属网络的合理模型。为了模拟人类活动的异质性，每个参与者 vj ∈ V 被规定一个随机权重 yj 反映他们的活动。类似地，为每个属性 wi ∈ W 规定了一个随机权重 xi 来模拟其吸引力。现在一个属性wi ∈ W 随机包含在集合Svj 中，并且概率与吸引力xi 和活动yj 成正比（参见，[14]，[17]）。通过这种方式，我们获得了顶点集 V 上的随机图，有时称为非齐次随机相交图，参见 [5] 和其中的参考文献。在给出这个随机图模型的详细定义之前，我们提到了最近的一篇出版物 [16]，该出版物令人信服地指出，在某些社交网络中，“重尾度分布是由人类活动的类似倾斜分布因果决定的”。 [16] 中报告的经验证据表明，非均匀随机相交图可以被视为幂律隶属网络的现实模型。

严谨的模型。让 $X_1, . . . , X_m, Y_1, . . . , Y_n$ 是独立的非负随机变量，使得每个 $X_i$ 的概率分布为 $P_1$，每个 $Y_j$ 的概率分布为 $P_2$。给定已实现的值 $X = \{X_i\}^m_{i=1}$ 和 $Y = \{Y_j\}^n_{j=1}$，我们定义随机二分图 $H_{X,Y}$ 与二分 V ∪ W ，其中 $V = \{v_1, . . . , v_n\}$ 和 $W = \{w_1, . . . , w_m\}$。每对 $\{w_i, v_j\}$ 在 $H_{X,Y}$ 中以概率链接

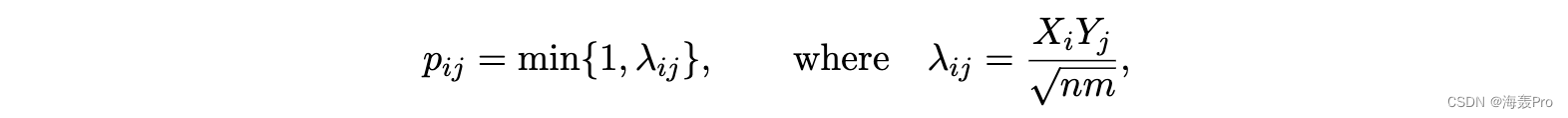
独立于其他对 $\{w, v\} ∈ W × V$ 。对于较大的 n 和 m，我们通常使 $λ_{ij} < 1$，因此概率 $p_{ij} = λ_{ij}$ 与 $v_j$ 的“活动” $Y_j$ 和 $w_i$ 的“吸引力” $X_i$ 成正比。非齐次随机相交图 $G = G(P_1, P_2, n, m)$ 定义了顶点集 V 上的邻接关系：当 u 和 v 有共同的邻居时，顶点 u, v ∈ V 被声明为相邻（表示为 u∼v）在 HX,Y 中。我们称这个邻居为邻接关系 u ∼ v 的见证人。

随机图 G 有几个特点，使其成为真实复杂网络的便捷理论模型。首先，Gmimics 中相邻邻接关系与实际隶属网络的统计相关性。特别是，G 承认一个可调的聚类系数： 对于 m/n → β ∈ (0, +∞) 作为 m, n → +∞，我们有，参见 [7]，

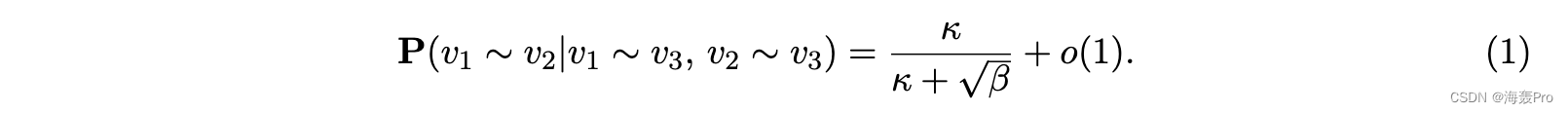
这里 κ := b1b−1 2 a3a−2 2 和 ai = EXi1, bj = EY j1 。其次，该模型的一个重要特征是它能够产生丰富的（渐近）度分布，包括幂律。 Letd(v) 表示顶点 v ∈ V 在 G 中的度数。我们注意到，通过对称性，随机变量 d(v1), 。 . . , d(vn) 具有相同的概率分布。 [4] 的以下结果将 d(v1) 的渐近分布描述为 n, m → +∞。

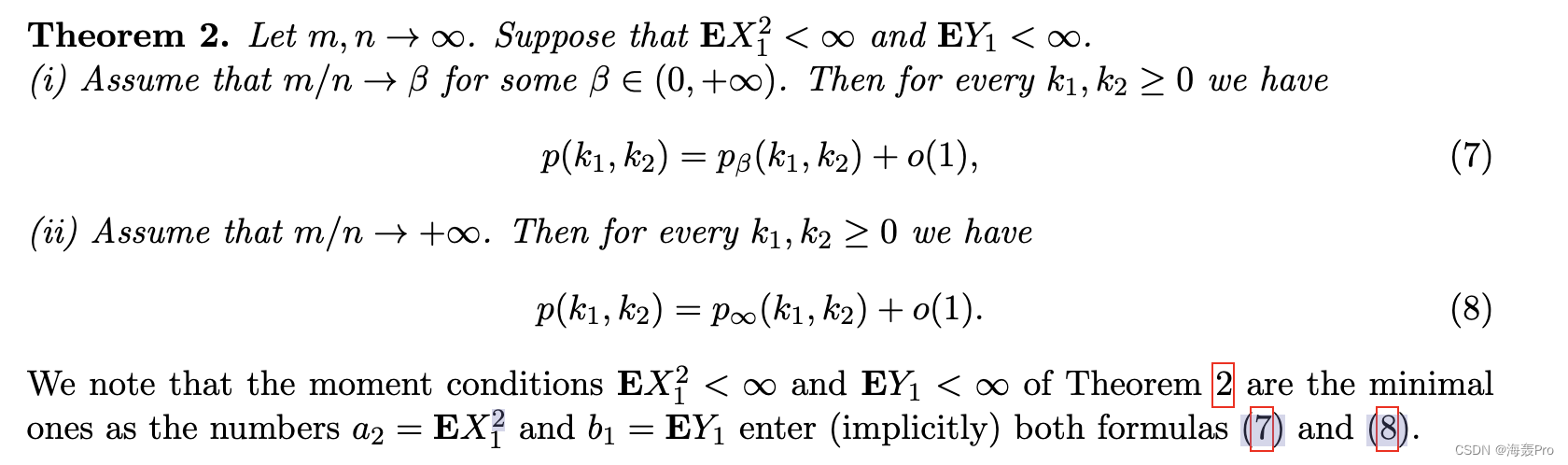
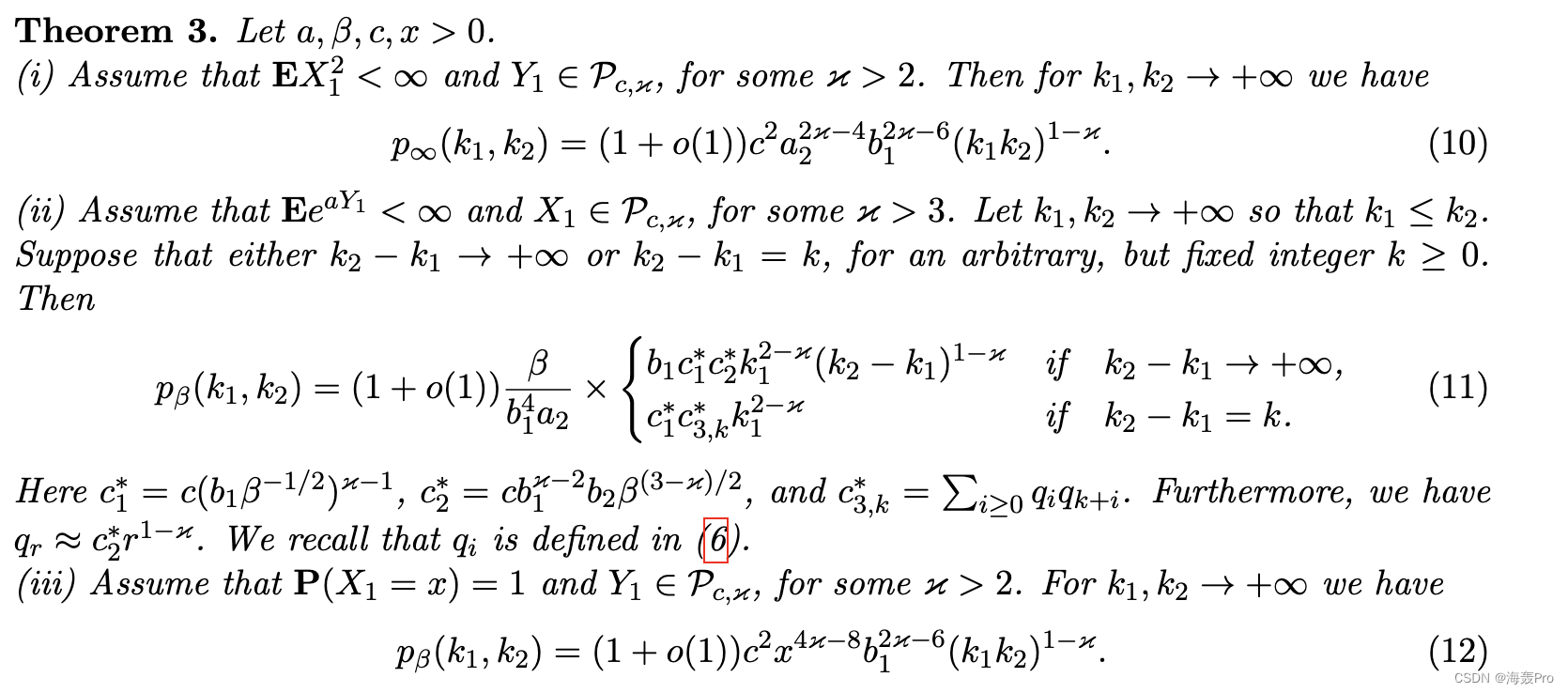
相关工作。许多作者已经研究了度-度相关性对网络属性的影响，参见例如 [8]、[12]、[18]、[19] 和其中的参考文献。具有可调幂律度分布的优先依附随机图中的渐近度度分布如[11]所示。我们的模式和方法大不相同。据我们所知，本文是第一次尝试在幂律网络中追踪度数分布与聚类属性之间的关系。纽曼的分类系数和相关随机图模型中的聚类系数之间的联系已经在[6]中讨论过。

剩余内容是上面三个定理的证明材料… （看不太懂了 哈哈）

结语

文章仅作为个人学习笔记记录，记录从0到1的一个过程

希望对您有一点点帮助，如有错误欢迎小伙伴指正