✅作者简介：人工智能专业本科在读，喜欢计算机与编程，写博客记录自己的学习历程。
🍎个人主页：小嗷犬的博客
🍊个人信条：为天地立心，为生民立命，为往圣继绝学，为万世开太平。
🥭本文内容：[做初中数学题做到打起来了]跟同事为了他小孩的数学题杠上了

@TOC

1.前情提要

这是2019年 NGA 论坛上的一个帖子：

帖子中提出了一个问题：4只小鸭子在一个大的圆形水池中，分别随机的出现在圆圈中的任意一点。4只鸭子出现在同一个半圆内的概率是多少?

这个问题当时分歧很大，各种答案都有，笔者当时看的也是一头雾水。

好在笔者现在学会了如何使用21世纪最先进的计算工具^1来进行计算，本文笔者将使用蒙特卡洛方法^2来解决本题。

2.蒙特卡洛方法

蒙特卡洛方法解此题的思路为：每次在圆周上生成4只鸭子，统计4只鸭子在同一半圆的次数与总次数的比例，即为4只鸭子出现在同一个半圆内的近似概率。

而是否在同一半圆则可以通过判断每只鸭子扫过半圆是否经过另外3只鸭子来判断。

所以我们可以得到以下代码：

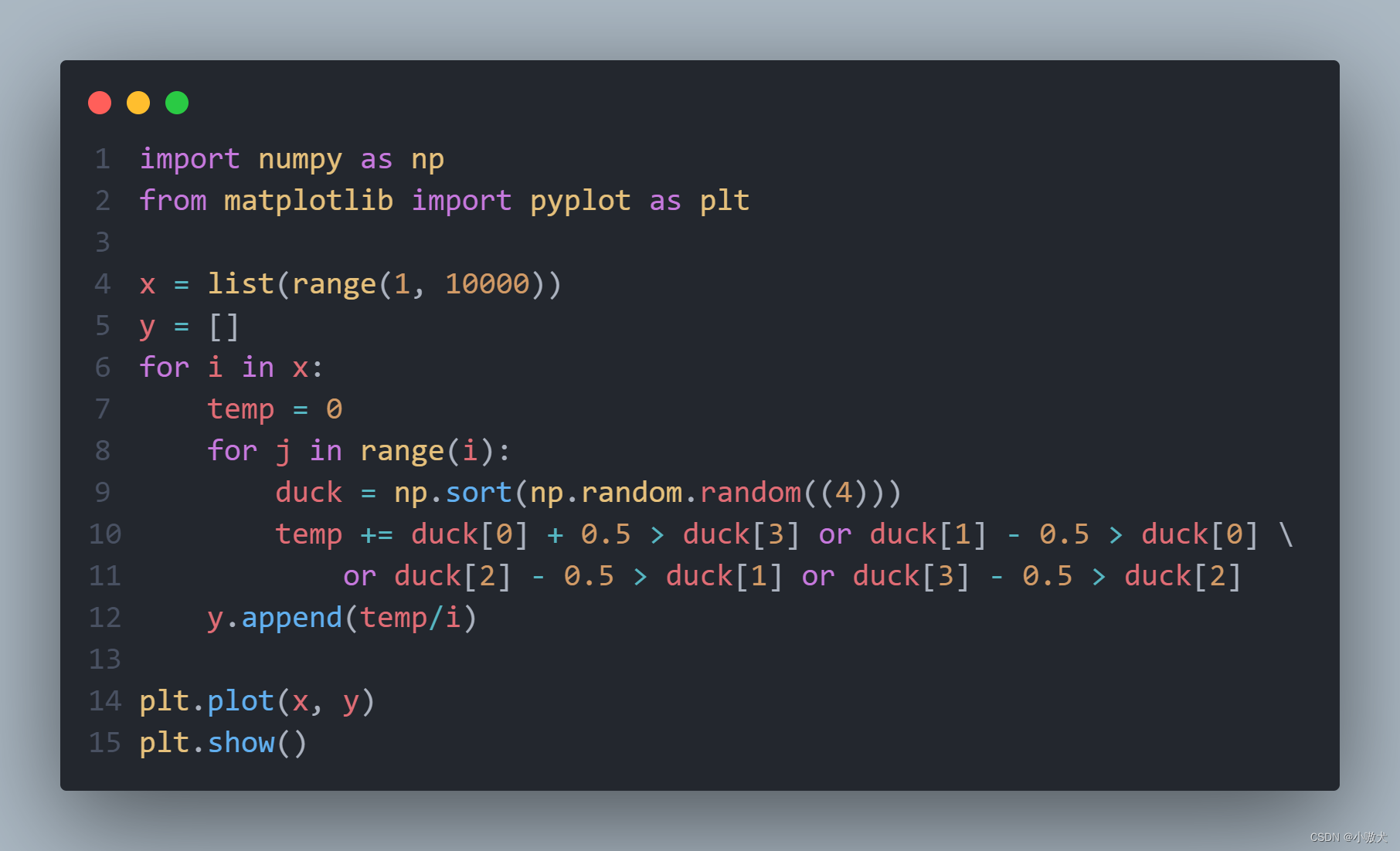
import numpy as np
from matplotlib import pyplot as plt

x = list(range(1, 10000))
y = []
for i in x:
    temp = 0
    for j in range(i):
        duck = np.sort(np.random.random((4)))
        temp += duck[0] + 0.5 > duck[3] or duck[1] - 0.5 > duck[0] \
            or duck[2] - 0.5 > duck[1] or duck[3] - 0.5 > duck[2]
    y.append(temp/i)

plt.plot(x, y)
plt.show()

通过增加随机次数，我们可以看到概率逐渐收敛到 $\frac{1}{2}$ ：

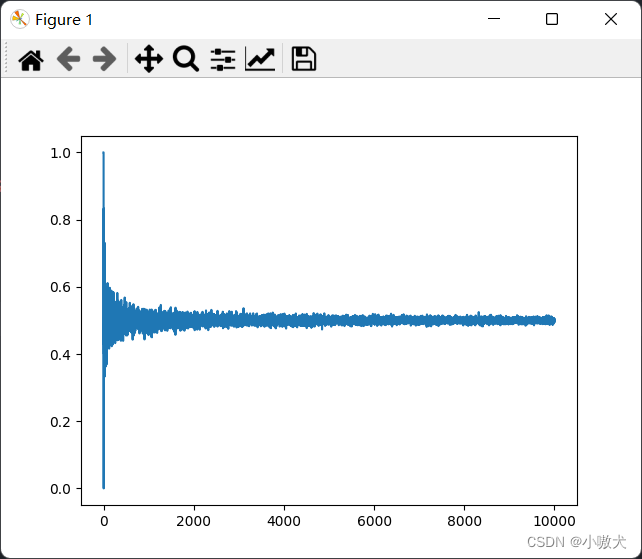
理解起来有多种思路，这里我采用了我认为最好理解的一种：

• 4只鸭子在水池中时，至少有3只会处于同一半圆^3。
• 这时4只鸭子出现在同一个半圆内的概率完全取决于最后那只鸭子。

3.尾声

本题本质上还是个数学问题，可以通过微积分进行求解。

但是现实中，4只鸭子出现在同一个半圆内的概率则不大可能是 $\frac{1}{2}$。

毕竟鸭子是集群动物，4只鸭子在一起应该是常态，那么它们是否处于同一半圆则主要取决于水池的大小了。

你们认为本题的答案是多少呢？欢迎在评论区留言。