@TOC

简介

Hello！
非常感谢您阅读海轰的文章，倘若文中有错误的地方，欢迎您指出～
 
ଘ(੭ˊᵕˋ)੭
昵称：海轰
标签：程序猿｜C++选手｜学生
简介：因C语言结识编程，随后转入计算机专业，获得过国家奖学金，有幸在竞赛中拿过一些国奖、省奖…已保研
学习经验：扎实基础 + 多做笔记 + 多敲代码 + 多思考 + 学好英语！
 
唯有努力💪
 
【每日一读】每天浅读一篇论文，了解专业前沿知识，培养阅读习惯（阅读记录 仅供参考）

论文简介

原文链接：https://ieeexplore.ieee.org/document/9835662

会议：2022 IEEE 38th International Conference on Data Engineering (ICDE) （CCF A类）

年度：2022年5月9日至12日（发表日期）

Abstract

网络嵌入，也称为网络表示，作为处理网络数据的基本工具，在数据挖掘和机器学习界引起了广泛关注。大多数现有的基于深度学习的网络嵌入方法都侧重于重建微结构的成对连接，这些连接很容易受到网络异常或攻击的干扰。

因此，为了应对上述挑战，我们提出了一种新的稳健框架，用于通过保留社区信息 (AnECI) 来进行属性网络嵌入。我们没有使用基于成对连接的微结构，而是尝试通过从数据本身学习的底层社区结构作为无监督学习来引导节点嵌入，以具有更强的抗干扰能力。

特别地，我们提出了一种新的高阶邻近和重叠社区的模块化函数来指导属性图编码器的网络嵌入。我们在真实基准数据集上对节点分类、异常检测和社区检测任务进行了广泛的实验，结果表明 AnECI 优于最先进的属性网络嵌入方法。

I. I NTRODUCTION

图或网络在现实世界中无处不在，例如社交网络、学术网络和蛋白质网络，其中属性网络是处理数据异质性的有力工具。除了仅对节点之间的交互进行建模的传统普通网络之外，每个节点的一组特征也包含在属性网络中。例如，在学术引用网络中，不同文章之间的引用构成了一个网络，其中每个节点都是一篇文章，每个节点都有文本信息，例如标题和摘要。在这些属性网络中，来自社会科学 [1] 的研究表明，节点的属性可以反映和影响其社区结构 [2]，这种洞察力有助于从网络中提取可操作的知识。由于网络拓扑结构和节点属性的高维和非欧式结构的复杂性，属性网络上的相关任务，包括社区检测、节点聚类和节点分类，带来了联合捕获结构和特征信息的挑战。为了解决这个问题，网络嵌入，也称为网络表示，作为处理网络数据的基本工具，最近在数据挖掘和机器学习界引起了极大的关注。它旨在学习网络中每个节点的低维表示，同时对网络结构信息进行编码。早期的网络嵌入方法通常基于拉普拉斯特征图[3]、矩阵分解[4]和随机游走[5]。

尽管这些方法由于结构浅而有局限性，但这些方法的成功验证了后续基于深度学习的方法的有效性。此外，这些基本方法只关注普通网络的拓扑结构，而忽略了信息丰富的节点属性。最近，专注于图深度学习的方法如雨后春笋般涌现，其中图卷积网络（GCN）[6]是一大进步。 GCN可以增强网络嵌入结果的表示能力，对属性网络有很大的适应性。由一个 GCN 编码器和一个重建解码器组成，图自动编码器 (GAE) 和变分图自动编码器 (VGAE) [7] 被提出来捕获高度非线性的特性，这可以很好地用于属性网络嵌入和下游任务。在这一点之后开发了一些先进的方法，例如 AGE [8]。然而，这些方法有两个主要限制。

• 首先，本质上，这些网络嵌入方法主要关注网络的微观结构，在新的嵌入空间中只保留每两个节点之间的成对连接或相似性[7]、[8]。然而，作为网络结构的重要细观描述，社区结构在上述这些方法中在很大程度上被忽略了。很自然，大多数网络都是由不同的社区组成的，这些社区被认为是一组节点，社区内的联系是密集的，而社区之间的联系是稀疏的。社区结构是网络最显着的特征之一[9]，它揭示了网络的组织结构和功能组成。因此，嵌入表示是否能够很好地反映社区结构是网络嵌入方法的关键要求，这对于属性网络也很重要。与微结构的成对连接不同，社区结构在更高的结构层面对节点表示施加了约束，即同一社区的节点表示应该比属于不同社区的节点表示更相似[10]。例如，由于数据稀疏性，属于同一社区的两个节点之间存在弱连接，但社区结构约束会加强它们的相似性。因此，将社区结构融入网络嵌入可以提供有效和丰富的信息来解决成对连接的微观结构中的数据稀疏问题，并且可以学习到更具判别力的节点表示。
• 其次，大多数基于深度学习的网络嵌入方法都非常容易受到网络攻击 [11] 或节点污染 [12]、[13] 的影响。当网络受到攻击或污染时，个别的虚假或异常边缘会起到误导作用[11]，甚至对节点进行轻微的干扰攻击也会导致很大的偏差。一些研究表明，节点的学习表示对微观结构的微小变化过于敏感，例如添加或删除边或节点[14]，以及下游任务的性能，例如节点分类或链接预测，将显着恶化 [15]。这通常是过分强调与局部结构的一阶邻近性而忽略社区结构的结果。如果可以考虑社区成员的无监督信息来指导网络嵌入，则结果将对攻击或节点污染具有鲁棒性。节点的社区所有权作为全局结构信息，不会因为网络结构的局部微小变化而轻易改变。

---

受上述观察的启发，我们提出了一个强大的属性网络嵌入框架，命名为保留社区信息的属性网络嵌入（AnECI）

• 首先，AnECI 使用图卷积编码器通过图卷积操作传播属性信息来学习属性网络的非线性嵌入。
• 其次，代替基于成对连接的模型学习，提出了一种新的模块化函数来指导网络嵌入，同时保留从数据本身学习的底层社区结构作为无监督学习，试图提高对局部网络异常值或攻击的鲁棒性。
• 此外，与传统的基于网络的一阶邻近性和基于硬分区的社区结构定义的模块化函数不同，我们为高阶邻近性和重叠社区结构开发了一种新的模块化函数。
• 此外，AnECI 将学习到的节点嵌入向量作为解码器来重构高阶邻近度，这也不同于传统方法通常重构一阶邻接矩阵。当有轻微攻击或节点污染时，高阶接近会比一阶接近更稳定，因为它在计算两个节点之间的接近时也考虑了更多的全局信息。据我们所知，我们的工作是第一次尝试将基于高阶邻近度的社区模块化纳入网络嵌入，并通过学习表示重建高阶邻近度。我们在真实基准数据集上对干净和攻击图的节点分类、异常检测和社区检测任务进行了广泛的实验，结果表明 AnECI 优于最先进的属性网络嵌入方法。

本文的贡献总结如下：

• 我们提出了 AnECI，一种鲁棒的网络嵌入模型，它增强了嵌入对抗对抗性攻击的鲁棒性。据我们所知，这是调查这项具有挑战性的任务的第一项工作。
• 我们提出了一种新的模块化函数，可以适应高阶邻近和重叠的社区结构，而不是传统的模块化函数只关注一阶邻近和基于硬分区的社区结构。
• 广泛的实验结果证明了所提出的方法在各种下游任务上的有效性。

II. R ELATED W ORK

A. Attributed Network Embedding

学习网络中节点的低维嵌入向量的网络嵌入在过去几年中备受关注，这可以追溯到传统的图嵌入[3]。受自然语言处理中的词嵌入 [16] 的启发，DeepWalk [5] 和 Node2Vec [17] 是首批在网络上执行随机游走以生成节点序列并通过 skip-gram 模型学习表示的作品。对于属性网络，早期的研究[18]利用矩阵分解技术将节点嵌入属性网络中，最近深度学习技术被广泛用于网络嵌入。

其中一组方法是基于普通数据上的传统深度神经网络，其中 SDNE [13] 和 DANE [19] 使用传统的自动编码器模型通过保留一阶和高阶网络邻近度来重构数据特征或邻接矩阵.最近提出的另一类模型通过图卷积操作来学习节点的嵌入，展示了卓越的性能。特别是，图卷积网络（GCN）[6]以给定的特征作为初始表示，通过图卷积的多层信息传播来实现节点的深度嵌入。 GraphSage [20] 将其扩展为通过学习聚合函数来实现归纳学习，而 DGI [21] 建议最大化路径表示和图的高级摘要之间的互信息。

此外，一些研究结合了图卷积网络和自动编码器的思想。例如，图自动编码器 (GAE) 和变分图自动编码器 (VGAE) [7] 提出通过 GCN 对网络进行编码，然后通过内积对其进行解码，以通过最小化交叉熵损失来重建边缘。继 GAE (VGAE) 之后，[22] 进一步利用图注意力网络 [23] 在聚合信息时分配邻居的不同权重。 AGE [8] 提出了一种自适应图编码器，它迭代地增强过滤后的特征以获得更好的节点嵌入，同时保留网络结构和属性信息。在海量数据上嵌入属性网络的可扩展性也引起了一些关注，并且已经开发了基于随机游走的方法 [24]、[25]。

B. Network Embedding for Outlier Detection

上述网络嵌入方法只关注干净的网络数据，没有考虑异常值（节点/边）的影响，因此容易受到影响。因此，最近的网络嵌入工作试图检测网络中的异常并取得了最先进的结果。提出了一种基于半监督深度学习的方法 SEANO [26]、基于无监督深度学习的方法 Dominant [12] 和基于无监督矩阵分解的方法 ONE [14]，用于属性网络的异常值检测和网络嵌入。例如，Dominant [12] 通过 GCN 显式地对图进行编码，并无缝地重构拓扑结构和节点属性以进行网络嵌入。类似地，DONE [15] 和 AnomolyDAE [27] 通过结构自编码器和属性自编码器共同学习嵌入，其中 DONE 还保留了节点之间的同质性，并通过最小化它们之间的差异将结构嵌入与属性嵌入连接起来。 ADONE [15] 进一步探索了对抗性学习在区分嵌入和以耦合方式最小化异常值的影响方面的作用。

C. Adversarial Attack and Defense for Graph Neural Networks

人们普遍认为，深度学习模型容易受到对抗性攻击，而图神经网络（GNN）不可避免地会遇到这样的问题，即对输入图的轻微或微不足道的干扰可能会使神经网络输出错误的预测[28]。对抗性攻击的基本思想是扰乱图结构和节点属性，使图神经网络模型无法正确分类某些节点，尤其是添加/删除/重新连接边。根据不同的设置，有不同种类的攻击。规避攻击将在训练阶段之后生成新的假样本，而中毒攻击试图在训练过程之前改变训练样本[29]。此外，攻击可以集中在对某些目标节点进行错误分类或仅仅降低整体分类性能，如目标 [11] 或非目标攻击 [29]。在针对性攻击中，直接攻击是指对目标节点的边缘或特征进行直接操纵，而影响攻击只能修改目标节点以外的其他节点。

显然，图对抗攻击对 GNN 的鲁棒性提出了很大挑战，严重限制了 GNN 在实际应用中的适用性。因此，最近提出了一些工作来提高 GNN 的鲁棒性并防止它们受到对抗性攻击。其中，RGCN[30]采用高斯分布作为每个卷积层中节点的隐藏嵌入，而不是将节点表示为向量； [31]发现nettack导致图的高秩谱的变化，建议使用低秩近似对图进行预处理。Pro-GNN [32] 提出从低秩、稀疏和同质性等常见图属性引导的扰动图中联合学习结构图和鲁棒图神经网络模型。关于图神经网络的对抗性攻击和防御的综合调查可以在 [33] 中找到

值得注意的是，所有这些防御模型都是为了提高半监督任务的鲁棒性，例如节点分类。与前面提到的异常值感知网络嵌入或网络防御方法不同，我们尝试探索基于高阶接近度的社区结构，以无监督的方式引导节点表示，这使得我们提出的模型无论有意对抗都表现出更强的鲁棒性攻击或无意的异常值。据我们所知，这将是它的第一部作品。

III. P RELIMINARIES AND D EFINITIONS

定义 1 属性网络。属性网络通常由图 G = (V, E, X) 表示，其中 V = {v1, v2,···, vN} 表示 N 个节点（或称为顶点）的集合。 E ⊂ {(vi, vj )|vi, vj ∈ V} 是每条边连接图中两个节点的边集，其中边的总数为 M 。根据边是对称的还是不对称的，网络可以是无符号的或有符号的。 X = {x1, x2, · · · , xN }T ∈ RN ×d 为特征矩阵，其中每一列向量 xi ∈ Rd 为节点 vi ∈ V 对应的 d 维属性向量，xj i 为第 j-节点 vi 的属性向量的第 th 项。例如，如果观察到文本描述，它可能是每个节点的 TF-IDF 向量。

定义 2 一阶邻近度。基于边集E，网络G的一阶拓扑结构通常用邻接矩阵A = {Aij} ∈ RN ×N表示，其中Aij = 1，表示节点vi和vj之间存在边。为了保持一般性，将自连接添加到图中，因此 A 中的对角元素为 1.D = diag(d1, d2, · · · , dN ) ∈ RN ×N 可以表示度矩阵，其中每个元素di 对应于连接到关联节点vi 的节点总数。

定义 3 高阶接近度。给定邻接矩阵 A，高阶邻近度 [34] 矩阵 ̃A = { ̃Aij } ∈RN ×N 定义为 A 的多项式函数：

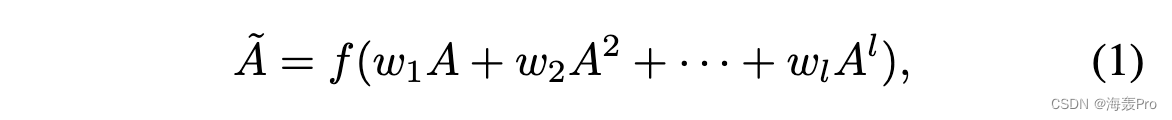
其中 l 是订单； w = [w1, w2, · · · , wl] 表示每个商品的权重向量，以平衡每个订单的结构信息； Al 表示 l 阶邻近矩阵，定义为：Al = ∏l i=1 A. f (·) 表示将矩阵 ̃A 保持在特定尺度的逐行归一化，使得 ̃Aij ∈ [0, 1]可以被认为是节点 vj 在高阶空间完全连接到 vi 的概率。

定义 4 社区结构。社区结构表示节点 V 在网络 G 中的划分。令 C = {c1, c2, · · · , c|C|} 表示社区标签集，且 P = {p1, p2, · · · , pN }T ∈ RN ×|C|表示社区成员指标矩阵。如果每个节点的列向量 pi 被约束为 one-hot 向量，则社区结构是硬分区。 pk i 可以看成 vi 属于社区 ck 的概率，每行 P 之和为 1，使社区结构成为一个具有软权重的重叠分区。

定义 5. 归因网络嵌入。属性网络嵌入的目的是将每个节点映射到一个低维表示 Z = {z1, z2, ···, zN }T ∈RN ×h，其中每个列向量 zi ∈ Rh 表示节点的学习表示六。自然地，学习到的嵌入矩阵应该保持社区结构和高阶接近度。

本文中使用的主要符号总结在表 I 中。

IV. M ETHODOLOGY

A. Overall Framework

我们提出的 AnECI 的框架如图 1 所示，由三个模块组成：

• 图卷积网络的归因网络编码器。图卷积网络模块作为网络编码器来学习每个节点的非线性潜在嵌入。
• 高阶模块化的社区保护。为了获得针对网络异常或攻击的更鲁棒的节点嵌入，嵌入空间中节点的表示应与社区结构相关，该结构由模块化函数指导，假设属于同一社区的节点应具有高度接近性。
• 高阶网络邻近重建。除了保留社区的细观结构外，学习的节点嵌入还可以重建高阶成对邻近度。

B. Graph Convolutional Encoder

属性网络编码器旨在将属性图 G 嵌入到低维空间中。一个有效的编码器应该捕获属性网络的基本属性，这是一项艰巨的任务，因为要同时解决三个问题，即网络稀疏性、数据非线性和复杂的模态交互。为此，受图卷积网络 (GCN) [6] 的启发，我们建议通过平滑和传播网络上的属性信息以及输入属性的非线性变换来对属性网络进行编码。因此，它可以缓解节点之间观察到的连接之外的网络稀疏问题。同时，通过多层非线性变换，捕捉数据的非线性以及属性网络上两种信息模态的复杂交互。

具体来说，GCN 将卷积操作扩展到谱域中的网络数据，并通过谱卷积函数学习新的潜在表示：

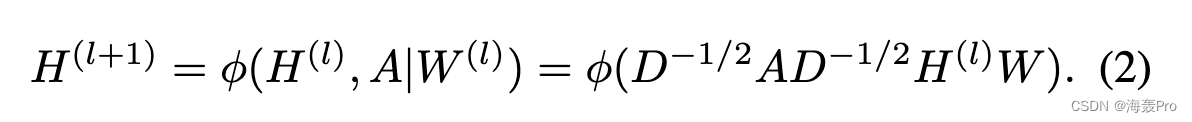
这里，φ(·) 是激活函数，例如 sigmoid 和 LeakyReLU 。在实验中，我们使用 LeakyReLU (·) =max(0,·) + a ∗ min(0,·) 作为激活函数，a = 0.01.H(l) ∈ RN ×hland H(l+1) ∈ RN × hl+1 是第 (l+1) 个卷积层对应的输入和输出。我们将特征矩阵 X ∈ RN ×d 作为第一层的输入，即 H(0) = X；最后一层是学习的嵌入矩阵，记为 Z ∈ RN ×h。

为了使每个节点的嵌入包含社区结构信息，如果我们将嵌入维度 h 设置为社区数量 |C|，我们可以从 Z 推断社区成员资格。一般我们通过soft tmax map将学习到的embedding矩阵Z转化为soft community members矩阵P，使得每个元素都在0到1之间，每行之和为1，为：

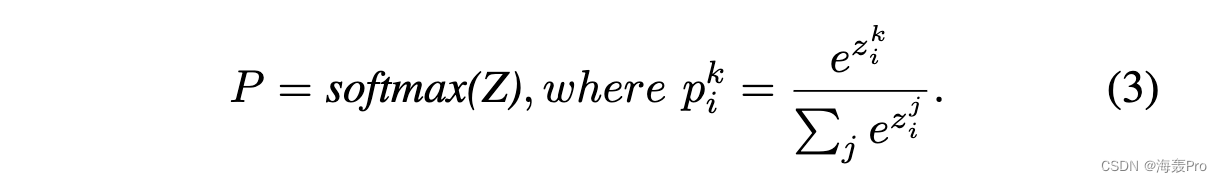
C. Modeling Community Structure by High-order Modularity

1）重新审视传统的模块化函数：作为最广泛使用的方法之一，基于模块化最大化的社区检测被用于对社区结构进行建模，我们将通过重新审视首先将其扩展到高阶邻近和重叠社区结构传统定义。具体来说，给定一个网络邻近矩阵 A，它恰好是传统方式的邻接矩阵，模块化函数 [35] 定义为：

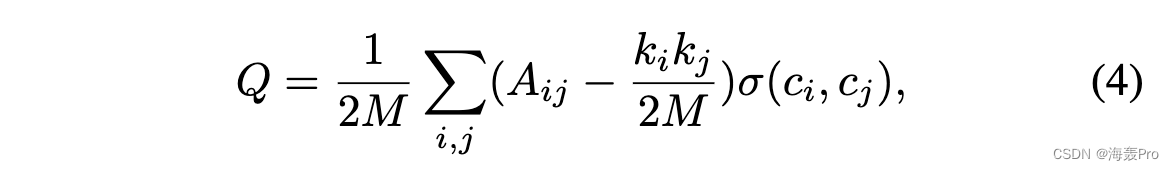
其中，Aij可以理解为两个节点vi、vj之间观察到的结构信息，即节点vi和vj之间的边；如果边是随机放置的，kikj /(2M ) 是这两个节点之间的预期结构信息，其中ki 表示节点 vi 的度数。 ci, cj 分别表示节点 vi, vj 的社区标签，σ(ci, cj ) 表示它们是否在同一个社区中，即 σ(ci, cj ) = 1，如果 ci = cj ，则为 0。因此，模块化直观地衡量社区内的边数与具有随机放置边的等效网络中的预期数之间的差异。模块化值越大，社区中包含的结构信息越大于期望值，这反映了网络的社区结构更加紧凑。

定义一个模块化矩阵 B = {Bij } ∈ RN ×N ，其中每个元素 Bij = Aij - kikj /(2M )，模块化可以重写为矩阵形式 [10]：

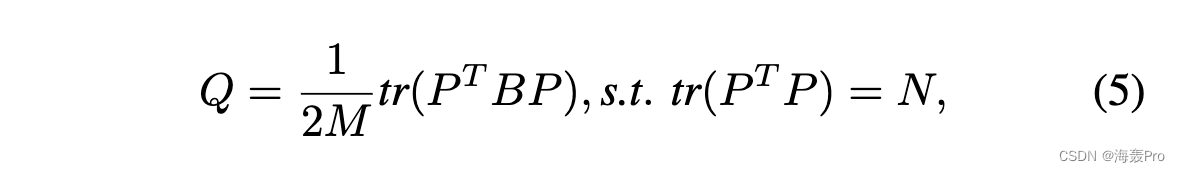
其中“tr(·)”表示方阵·的迹，由对角线元素之和定义； P ∈ RN ×|C|是社区成员指标矩阵，如定义4。在硬分区社区结构的传统定义中，每个行向量pi是一个单热向量，意味着只有一个元素为1，其他元素为0，受tr(P T P )约束= N

2. A Generalized Modularity Function：需要注意的是，上述(4)中的模块化定义仅强调一阶接近性，仅针对基于硬分区的社区结构。为了将其扩展到广义场景，即具有软权重的高阶邻近或重叠社区结构，我们首先提出以下模块化函数：

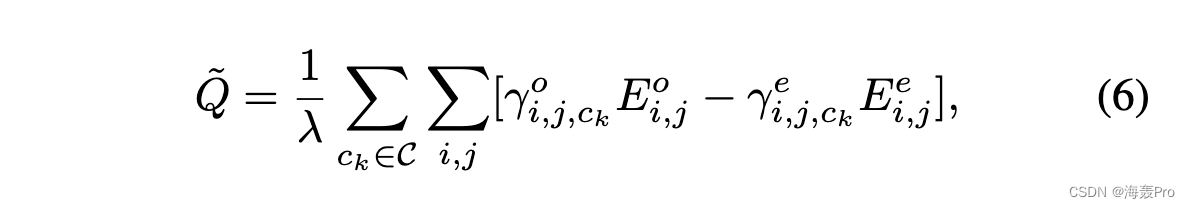
其中Eo ij 和Ee ij 可以分别理解为两个节点vi, vj 之间观察到的和预期的结构信息的广义形式。 γo i,j,ck 和 γe i,j,ck 是 Eo i,j 和 Ee i,j 对应的适应因子，衡量节点 vi 和 vj 之间的结构信息对社区 ck 的影响。具体来说，它们是 αi,ck 和 αj,ck 的非减函数，分别表示节点 vi 或 vj 对社区 ck [36] 的权重，如：

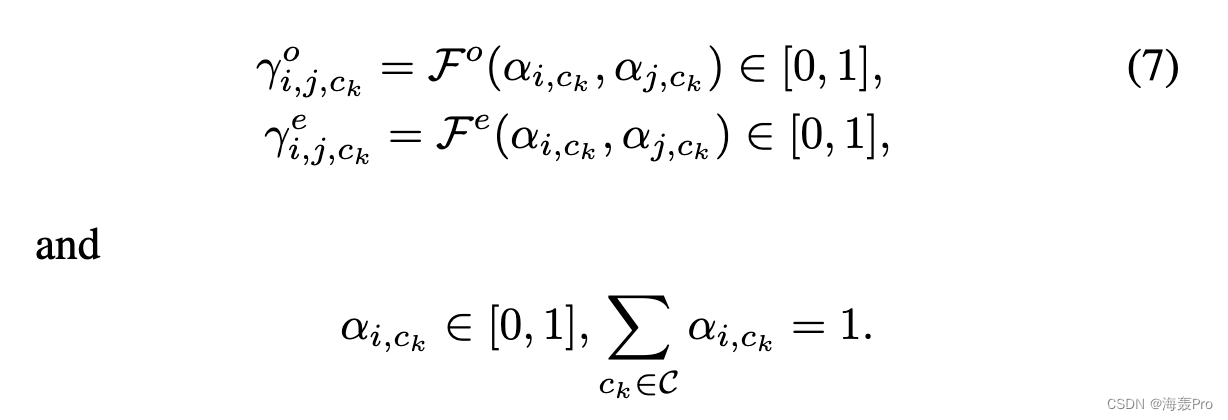
直观地说，γo i,j,ck 和 γe i,j,ck 应该满足以下两个等价条件：

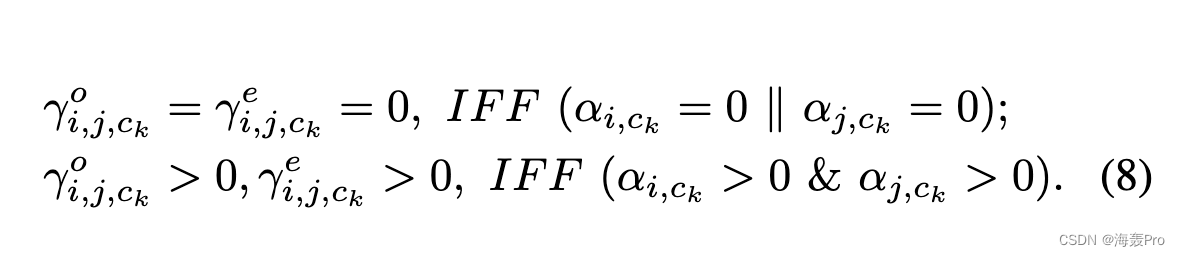
在 (4) 的传统一阶邻近度定义中，λ = 2M ； Eo ij 和 Ee ij 正好指 Aij 和 kikj /(2M )；γo i,j,ck 和 γe i,j,ck 由 σ(ci, cj , k) 测量； σ(ci, cj , k) = 1，如果节点 vi 和 vj 属于同一个社区 ck，否则为 0。在接下来的两个小节中，我们将展示如何在基于高阶邻近的社区划分和重叠社区结构上分别设计一个新的 (Eo ij , Ee ij ) 和 (γo i,j,ck ,γe i,j,ck )。

3）为高阶邻近性扩展模块化：对于具有社区结构的网络，同一社区中的许多节点通常不直接通过边连接。两个节点被分组到同一个社区的现象通常是由于它们之间的高阶接近性，因为它们可能直接连接到另一个中间节点。因此，基于一阶邻近度的社区只能表示一个简单的结构，但在现实生活中会更加复杂。此外，简单地使用从传统的一阶模块化函数导出的社区标签来指导节点表示学习，很容易受到异常值或攻击的影响，即不够鲁棒。因此，我们建议将模块化函数从一阶接近扩展到高阶结构信息。

因此，(6)中的Eo ij 和Ee ij 的定义可以扩展到高阶接近。由于 Al ij 是在计算从节点 vi 到节点 vj 在 l 跳中的不同路径的数量，描述了这两个节点之间的 l 阶接近度，所以 Al ij 在所有 ls 上的总和，即 ̃Aij 可以定义为总观测到的高阶结构信息 Eo ij 。类似地，̃ki ̃kj /(2 ̃M )可以表示两个节点之间期望的高阶结构信息Ee ij，其中̃ki = ∑j ̃Aij可以看作节点vi的高阶结构度，̃M = ∑i,j ̃Aij是所有高阶结构度的总和。

因此，模块化 ̃Q 的新定义如下：

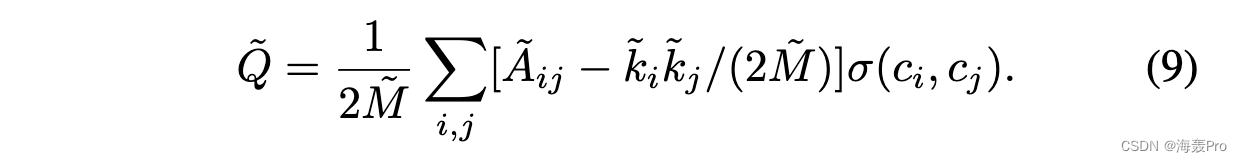
4. 为重叠社区扩展模块化：在传统的模块化功能中，社区结构是一种硬划分方式，即每个节点只属于一个社区。然而，由于网络结构复杂，社区成员之间联系紧密，导致节点之间存在一定的相似性，跨多个社区的属性也存在一定的相似性。另一方面，真正的复杂网络从未被划分为尖锐的子网络，尤其是那些由社交互动形成的子网络。例如，演员通常属于多个不同的社区，同时参与多个群体的活动。在本节中，我们尝试通过定义 γo i,j,ck 和 γe i,j,ck 将其扩展到具有软权重的重叠社区结构。

在提出我们的想法之前，我们首先提出扩展函数应符合的以下两个属性：

性质 1. 为了保持一般性，为重叠社区结构定义的模块化函数可以退化为基于硬分区的社区结构的通用模块化。

属性 2. 为重叠社区定义的模块化函数可以暗示节点属于不同社区的不同可能性。

为符合性质 1，应满足以下规则，即当对应的两个节点仅属于同一个社区 ck 时，γo i,j,ck 和 γe i,j,ck 都应为 1。

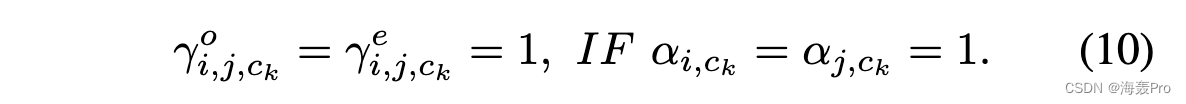
尽管重叠社区有多种模块化定义，但并不总是遵守这些属性。例如，[37]中的定义是：

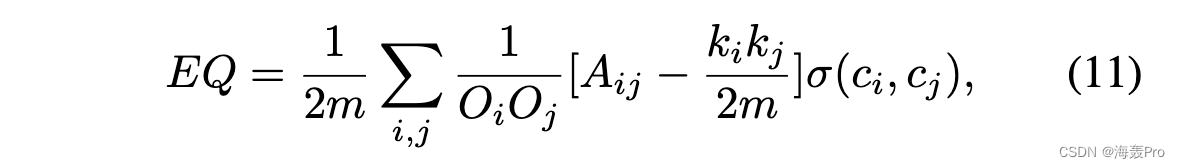
其中，Oi 是节点 vi 所属的社区数。显然，它符合性质 1，因为对于基于硬分区的社区结构，Oi 将始终为 1，而 EQ 将变为 (4) 中的 Q。但是，在式(11)中，1/(OiOj )可以看作是适应因子γ，显然不能适应为一个节点的不同社区分配不同权重的重叠社区。因此，（11）中的 EQ 不能符合性质 2。

此外，[36] 引入了具有重叠社区结构的网络的新定义，如：

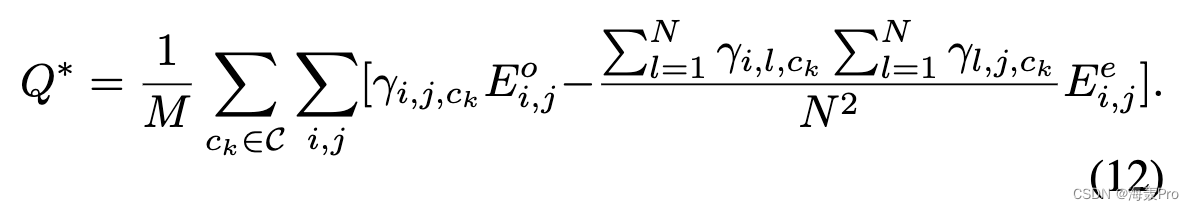
根据(6)中的框架，γi,j,ck and (∑N l=1 γi,l,ck∑N l=1 γl,j,ck )/N 2 可以理解为γo i,j,ckand分别为 γe i,j,ck。然而，（12）中提出的模块化函数不满足属性 1，我们可以简单地使用反证法来证明它，如下所示。假设它满足性质1，给定一个基于硬分区的社区结构，当节点vi和vj属于同一个社区ck时，即αi,cK = αj,cK = 1，我们有γe i,j,ck =∑N l= 1 γi,l,ck∑N l=1 γj,l,ckN 2 =∑N l=1 γi,l,ckN ∗∑N l=1 γj,l,ckN = 1，根据（10）。在这种情况下，由于（7）中的要求，γi,l,ck = γj,l,ck = 1 对于所有 vl 必须成立，即所有节点都属于同一个社区 ck 和 |C| = 1，这对于真正的社区结构是没有意义的。换句话说，如果存在多个社区，则 γe i,j,ck 永远不会达到 1。因此，(12) 中的模块化函数不满足性质 1。

基于上述分析，我们建议将式（12）中的定义修改为：γe i,j,ck = γo i,j,ck = F(αi,ck , αj,ck )。用相应的两个权重之间的乘积或最小值对 F(·) 的简单定义可以使 γo i,j,ck 和 γe i,j,ck 符合 (8) 和 (10)。在实验中，我们根据经验设置 F(αi,ck , αj,ck ) = αi,ck αj,ck 。因此，我们新提出的模块化函数定义为：

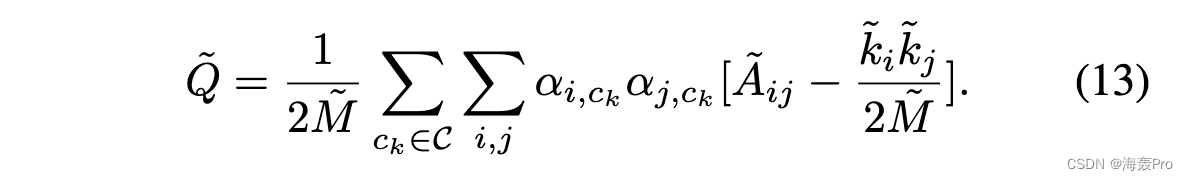
在矩阵形式中，它可以重写为：

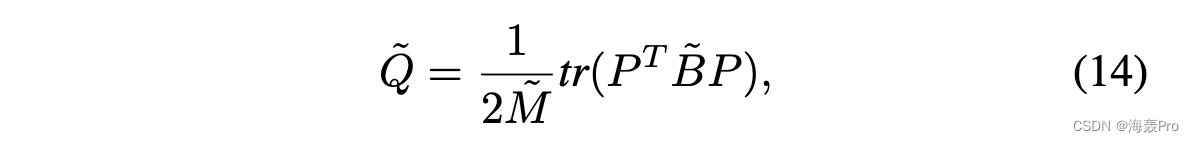
其中，P 是如式（3）中属性网络编码器得到的社区成员矩阵，其中 pk i 正是对应的权重 αi,ck ； ̃Bij = ̃Aij - ̃ki ̃kj /(2 ̃M )。因此，通过上述讨论，（13）中的定义同时符合性质 1 和性质 2。

D. High-order Proximity Reconstruction Decoder

在本小节中，我们将展示如何通过属性网络编码器模块的输出来重建原始网络结构。首先，我们将尝试重构 ̃A，而不是 GAE/VGAE [7] 中的邻接矩阵 A，因为高阶邻近度在计算邻近度时考虑了更多的全局信息，并且比一阶邻近度更稳定和稳健。如前所述，是轻微的攻击或节点污染。此外，我们利用社区成员矩阵 P 而不是 GAE/VGAE 中的嵌入矩阵 Z 来重建图结构，因为我们假设共享相似社区成员的两个节点更有可能在高阶空间中连接，这进一步增强了节点通过社区结构嵌入。在数学上，解码器将潜在嵌入 P 作为输入，并预测每对节点之间的高阶接近度：

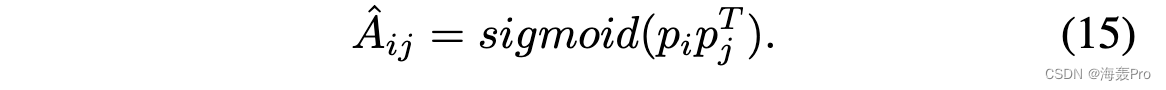
因此，在矩阵形式中，我们可以基于属性网络编码器 P 的输出来训练邻近度下降模块，如下所示：

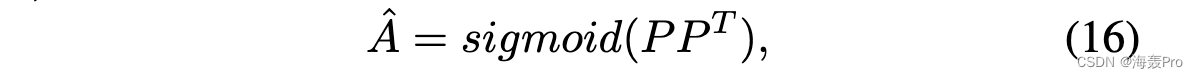
其中，^Aij = pipT j 衡量了节点 vi 和 vj 对应的隶属向量 pi 和 pj 之间的相似度，两个节点之间的相似度越高，它们在高阶空间中连接的概率就越高。因此， ^Aij ∈ [0, 1] 可以看作是节点 vj 在高阶空间完全连接到 vi 的估计概率。结合前面对(1)下归一化̃Aij的定义，我们可以推导出两个二项式概率分布，即[ ̃Aij , 1 − ̃Aij ]和[ ̃Aij , 1 − ̃Aij ]，其中1 − ̃Aij 和1 − ̃Aij 分别表示真或估计对应的两个节点在高阶空间中完全断开的概率。因此，这两种分布之间的差异可用于检测网络结构异常或攻击。换句话说，如果解码器可以高度重构两个节点之间的高阶接近度，则嵌入空间 Z 中对应的两个向量将很好地编码这些结构信息。形式上，高阶邻近重构解码器的损失可以定义为每个节点对上的广义交叉熵之和：

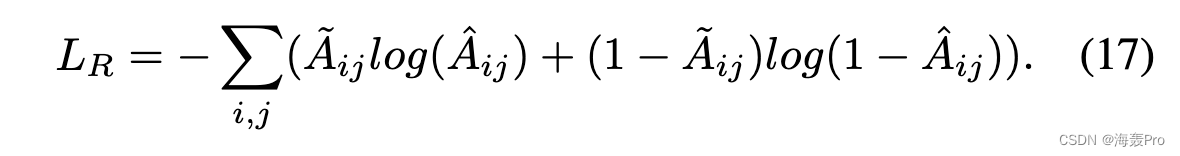
E. Robust Attributed Network Representation

到目前为止，我们已经介绍了如何通过 GCN 模块对属性网络进行编码，如何通过新的模块化函数保留社区结构，以及如何通过解码器重建高阶邻近度。为了共同学习潜在表示 Z，我们提出的 AnECI 的总目标函数可以表示为：

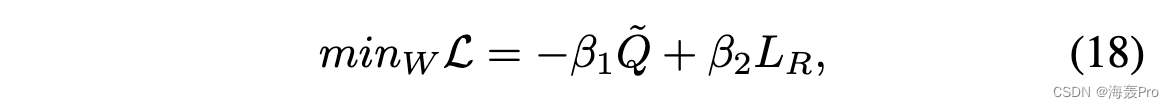
其中，β1和β2是平衡社区结构和高阶邻近重建贡献的超参数。通过最小化上述目标函数，我们提出的鲁棒图卷积自动编码器可以基于嵌入的潜在表示迭代地逼近输入属性网络，可用于下游任务。

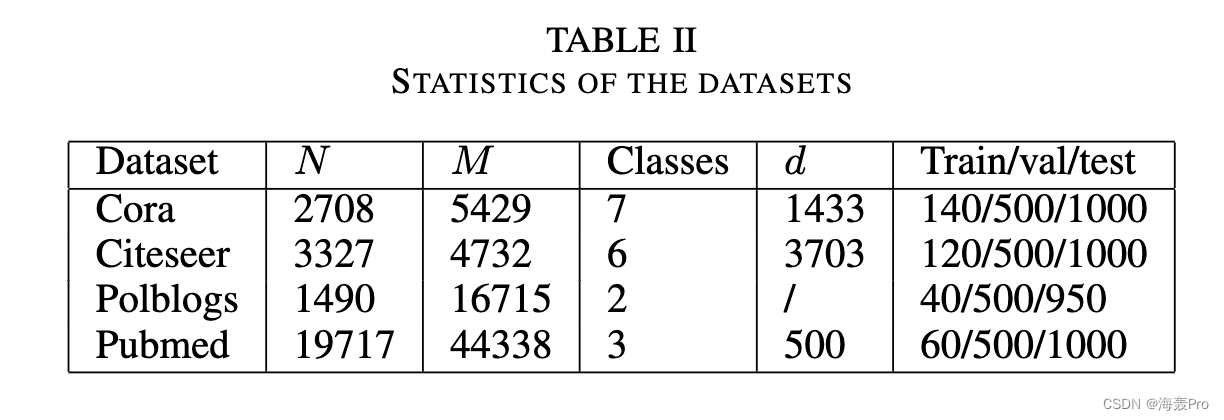
V. E XPERIMENTAL SETUP

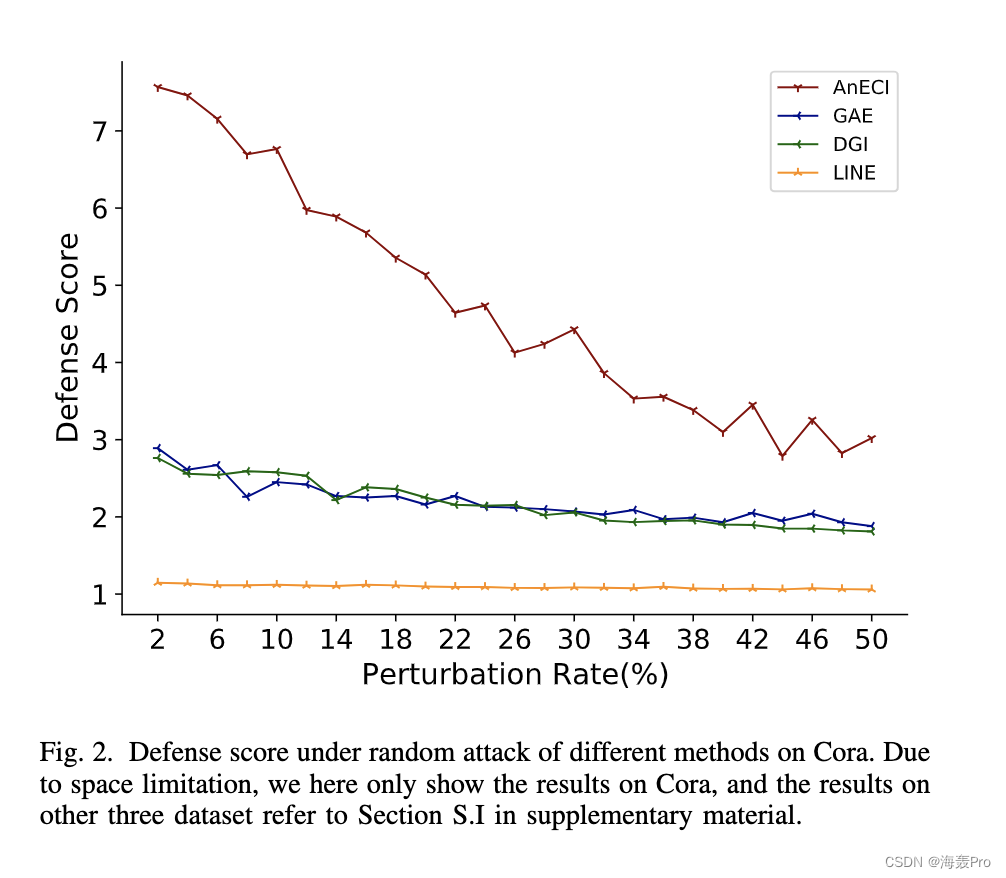
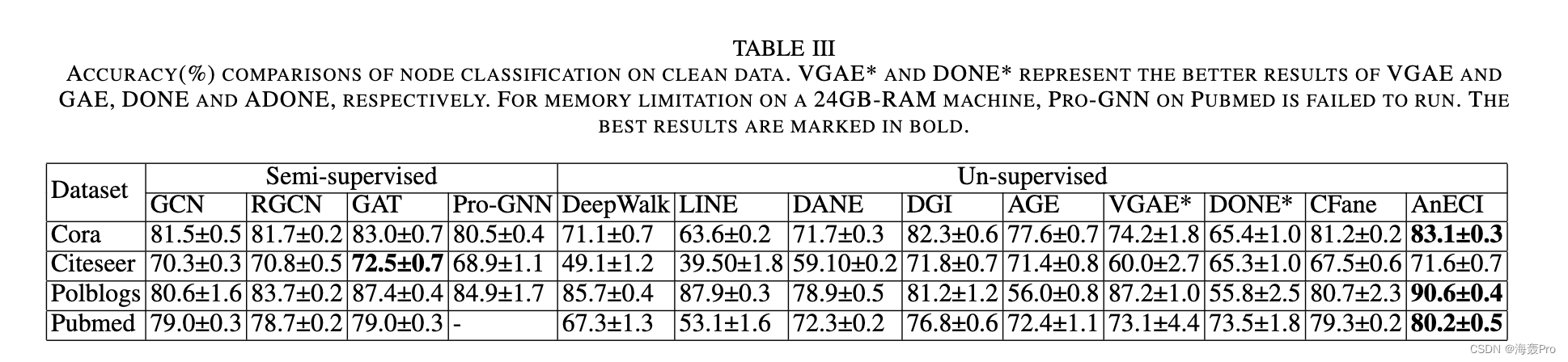
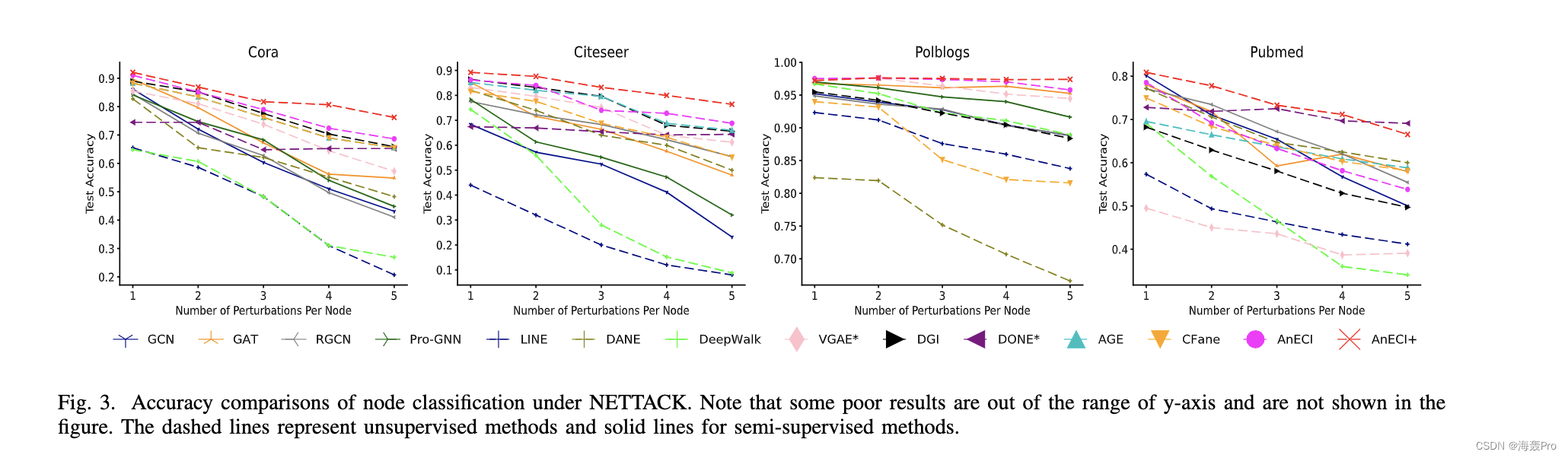
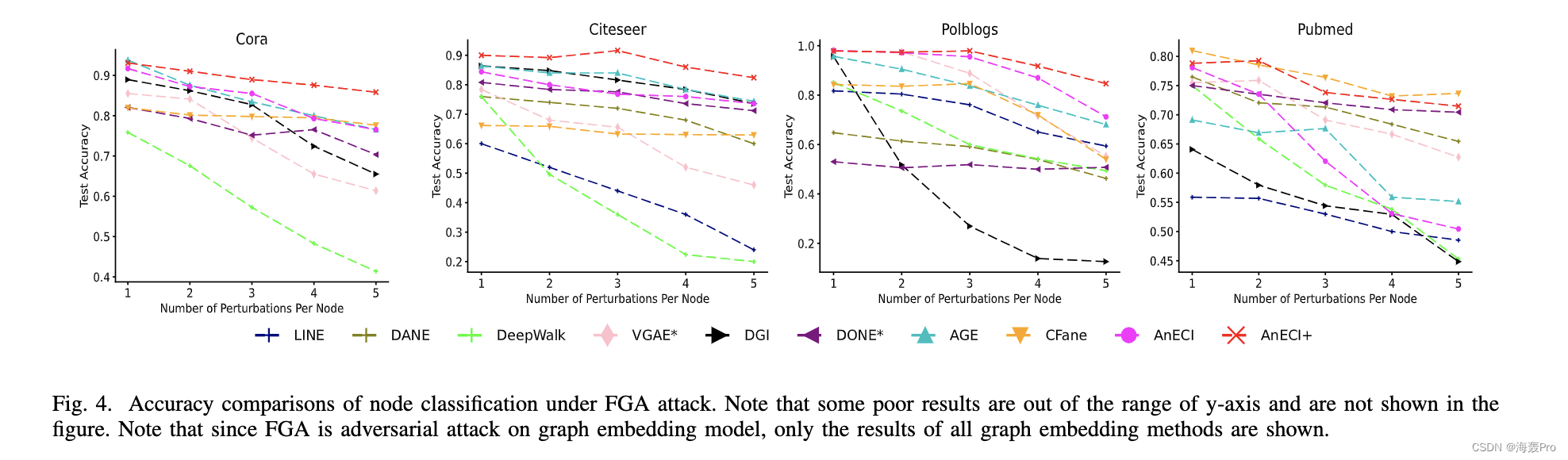
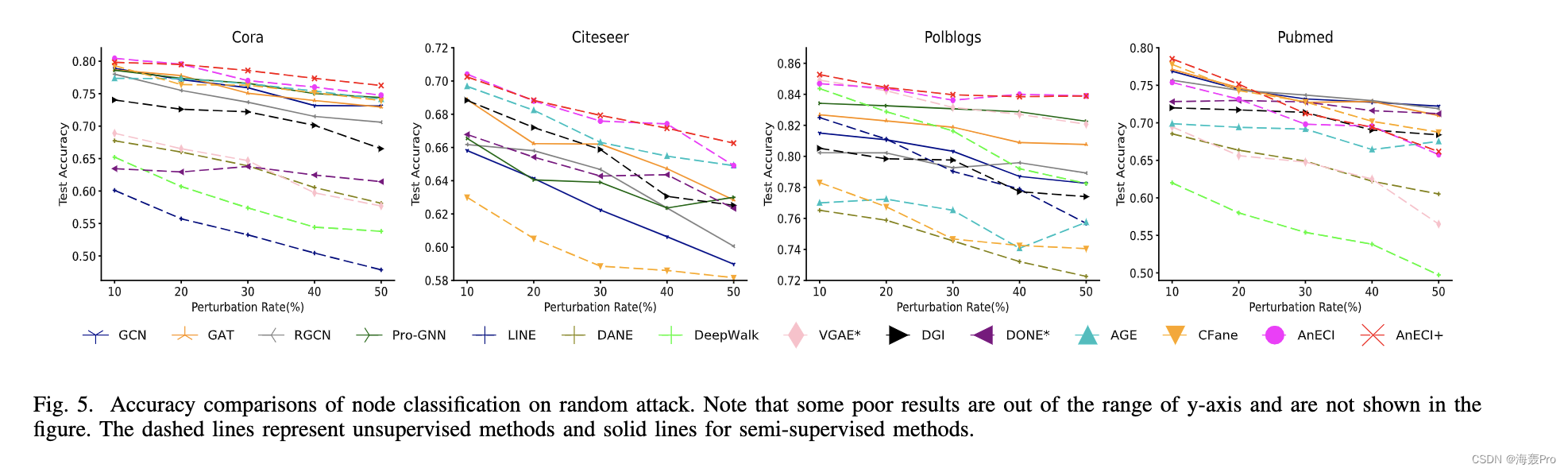
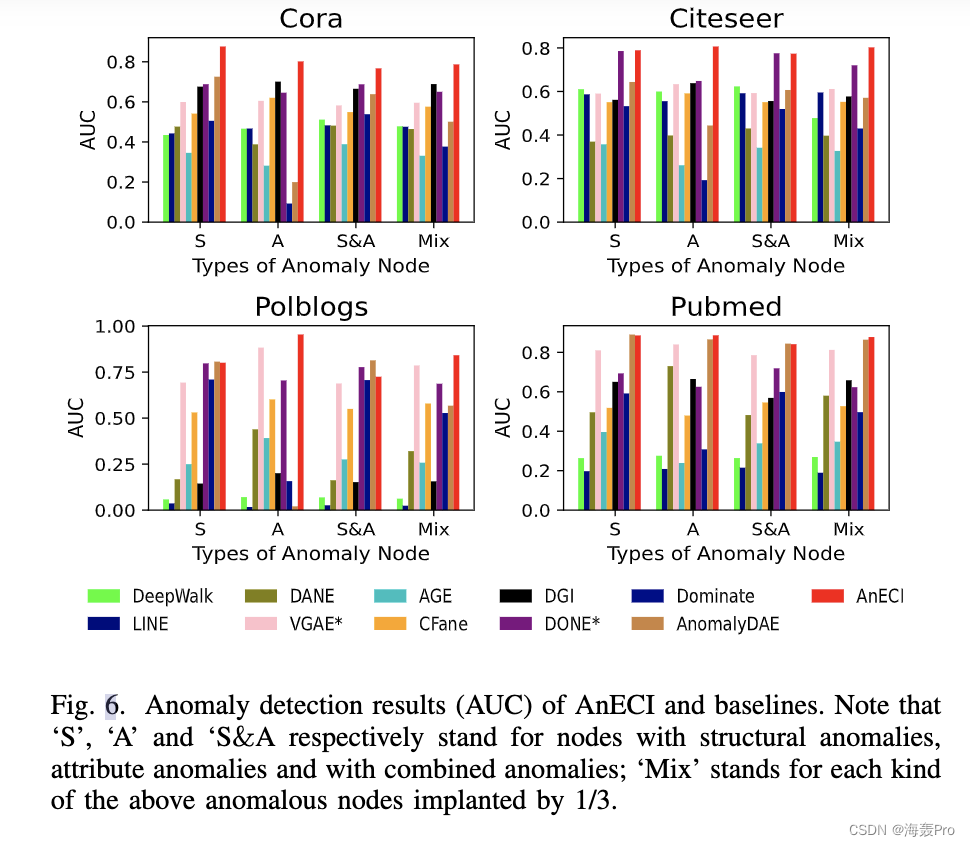
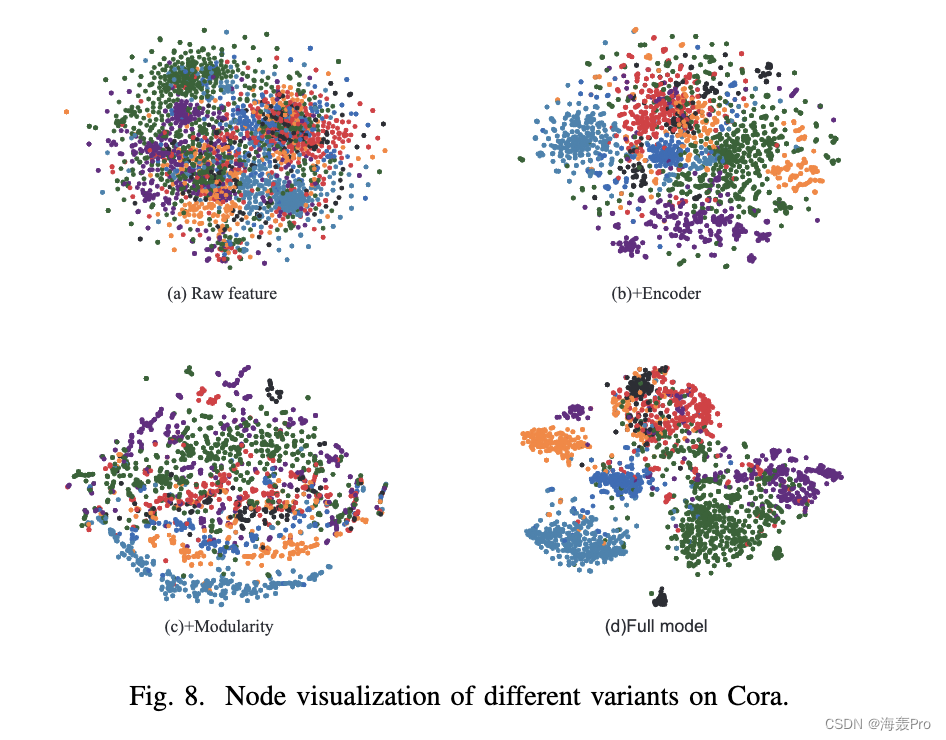
VII. C ONCLUSIONS

为了减轻网络异常值的影响和防御网络攻击对网络嵌入的影响，我们提出了一种鲁棒的属性网络嵌入保留社区信息（AnECI）。

AnECI 建议通过模块化函数来引导 GCN 编码器的网络嵌入，而不是成对连接，并保留由嵌入本身确定的社区结构信息作为无监督方式。

它试图提高通常本地网络异常值或攻击的鲁棒性，因为它以无监督的方式考虑全球社区结构。此外，AnECI 重构了高阶邻近度，当存在轻微攻击或节点污染时，它比一阶邻近度更稳健，因为它考虑了更多的全局信息。

对三个图挖掘任务的四个真实数据集进行了广泛的实验，结果表明 AnECI 相对于最先进的方法有了显着的进步。

未来，我们会尝试利用更多的属性来进一步提高网络嵌入对网络攻击或异常值的鲁棒性，并通过采样和学习聚合函数 [20] 而不是全图拉普拉斯传播来提高更大数据集的可扩展性。

结语

文章仅作为个人学习笔记记录，记录从0到1的一个过程

希望对您有一点点帮助，如有错误欢迎小伙伴指正