快速排序图解(两种思想)
七大排序之快速排序
前言
博主个人社区:开发与算法学习社区
博主个人主页:Killing Vibe的博客
欢迎大家加入,一起交流学习~~
一、《算法导论》中的分区思想
快速排序又是一种分而治之思想在排序算法上的典型应用。本质上来看,快速排序应该算是在冒泡排序基础上的递归分治法。
动图如下:

1.1 算法思想
快速排序是20世纪最伟大的算法之一
核心的思路就是分区
分区值:默认选择最左侧元素pivot(当然也可以随机选择)
- 从无序区间选择一个值作为分界点pivot开始扫描原集合
- 将数组中所有小于该pivot的元素放在分界点左侧
- 大于等于该元素的值放在分区点的右侧
- 经过本轮交换,pivot放在了最终位置,pivot的左侧都是小于该值的元素,pivot的右侧都是大于该值的元素,在这两个子区间重复上述过程,直到整个集合有序。
举个栗子:
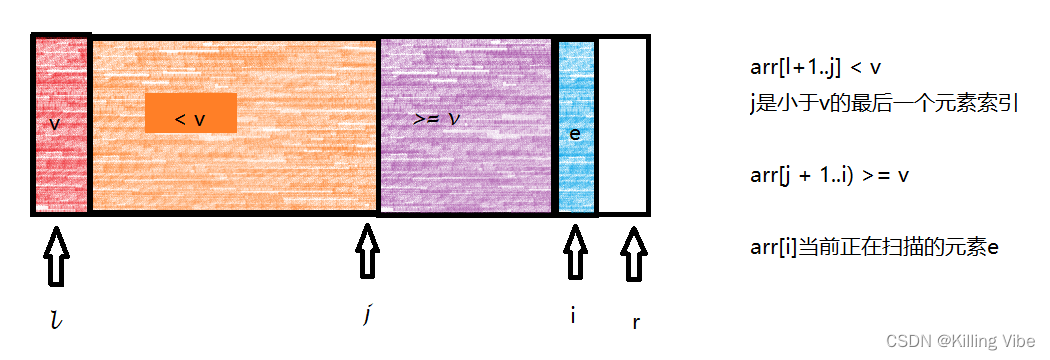
1.若arr[i] >= v
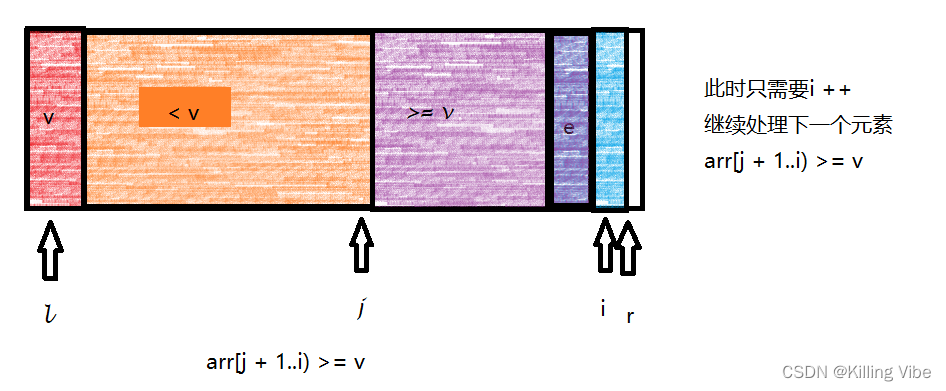
2.若arr[i] < v
索引 j 指向了最后一个 < v 的元素,而 j+1 恰好是第一个 >= v的元素
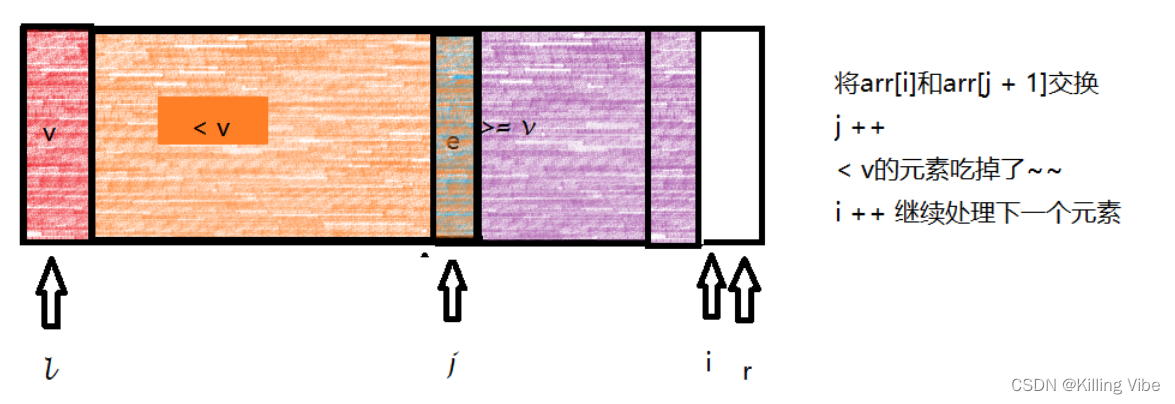
3.当 i 扫描完集合时,数组划分如下:

4.交换 l 和 j 所在的元素

5.橙色和紫色的部分继续重复上述过程即可
1.2 代码实现
代码如下:(请往后看)
private static void quickSortInternal(int[] arr, int l, int r) {
// 2.小区间上使用插入排序来优化,不用递归到底
if (r - l <= 15) {
insertionSort(arr,l,r);
return;
}
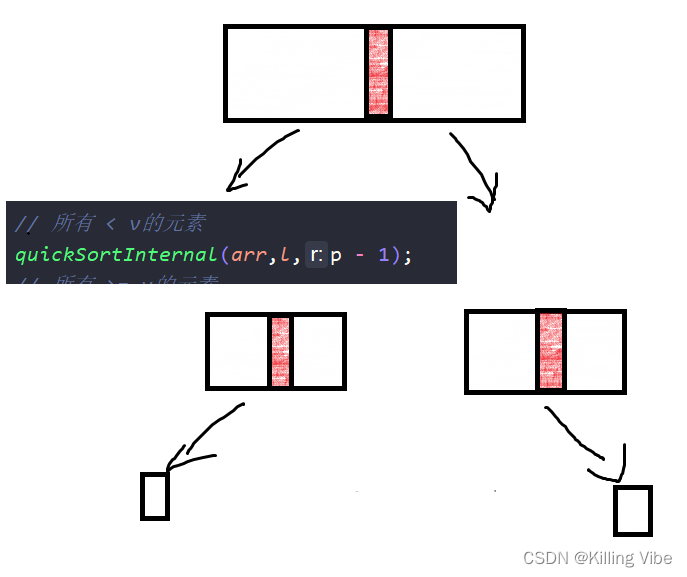
int p = partition(arr,l,r);
// 继续在左右两个子区间进行快速排序
// 所有 < v的元素
quickSortInternal(arr,l,p - 1);
// 所有 >= v的元素
quickSortInternal(arr,p + 1,r);
}
private static int partition(int[] arr, int l, int r) {
// 1.优化1.使用一个随机位置作为分区点,避免快排在近乎有序数组上的性能退化
int randomIndex = random.nextInt(l,r);
swap(arr,l,randomIndex);
int v = arr[l];
// arr[l + 1..j] < v
// 最开始区间没有元素
int j = l;
// arr[j + 1..i) >= v
// 最开始大于区间也没有元素
for (int i = l + 1; i <= r; i++) {
if (arr[i] < v) {
swap(arr,i,j + 1);
j ++;
}
}
// 此时元素j就是最后一个 < v的元素,就把v换到j的位置
swap(arr,l,j);
return j;
}
注意:这是优化后的代码

小数组采用插入排序可以提高性能,若不能理解可以把这段改成:
if (r - l <= 0) return;
非递归写法:
public static void quickSortNonRecursion(int[] arr) {
Deque<Integer> stack = new ArrayDeque<>();
// r
stack.push(arr.length - 1);
// l
stack.push(0);
// 每次从栈中取出两个元素,这辆个元素就是待排序区间的l..r
while (!stack.isEmpty()) {
int l = stack.pop();
int r = stack.pop();
if (l >= r) {
// 当前子数组已经处理完毕
continue;
}
int p = partition(arr,l,r);
// 继续入栈两个子区间
stack.push(p - 1);
stack.push(l);
stack.push(r);
stack.push(p + 1);
}
}
private static int partition(int[] arr, int l, int r) {
// 1.优化1.使用一个随机位置作为分区点,避免快排在近乎有序数组上的性能退化
int randomIndex = random.nextInt(l,r);
swap(arr,l,randomIndex);
int v = arr[l];
// arr[l + 1..j] < v
// 最开始区间没有元素
int j = l;
// arr[j + 1..i) >= v
// 最开始大于区间也没有元素
for (int i = l + 1; i <= r; i++) {
if (arr[i] < v) {
swap(arr,i,j + 1);
j ++;
}
}
// 此时元素j就是最后一个 < v的元素,就把v换到j的位置
swap(arr,l,j);
return j;
}
二、Hoare挖坑法
目前市面上和教科书上的常用分区方法。
2.1 算法思想
-
先从序列中随机选一个pivot,默认从最左边元素
-
将两个索引 i 和 j 分别从左右两边开始往中间遍历
-
先让 j 从后往前找到第一个 < v 的元素停止,把这个元素直接赋值给i所对应得元素。
-
再让 i 从前往后找到第一个 > v 的元素停止
-
当 i 和 j 重合时,arr[i] = pivot 即可~
没有元素交换的时候都是直接赋值,理论上会减少因为交换带来的时间损耗
2.2 代码实现
代码如下:
private static void quickSortInternalHoare(int[] arr, int l, int r) {
// 2.小区间上使用插入排序来优化,不用递归到底
if (r - l <= 15) {
insertionSort(arr,l,r);
return;
}
int p = partitionHoare(arr,l,r);
// 继续在左右两个子区间进行快速排序
// 所有 < v的元素
quickSortInternalHoare(arr,l,p - 1);
// 所有 >= v的元素
quickSortInternalHoare(arr,p + 1,r);
}
/**
* 挖坑分区法
* @param arr
* @param l
* @param r
* @return
*/
private static int partitionHoare(int[] arr, int l, int r) {
int randomIndex = random.nextInt(l,r);
swap(arr,l,randomIndex);
int pivot = arr[l];
int i = l;
int j = r;
while (i < j) {
// 先让j从后向前扫描到第一个 < v的元素停止
while (i < j && arr[j] >= pivot) {
j --;
}
arr[i] = arr[j];
// 再让i从前向后扫描到第一个 > v的元素停止
while (i < j && arr[i] <= pivot) {
i ++;
}
arr[j] = arr[i];
}
arr[i] = pivot;
return i;
}
三、算法分析
快速排序通常明显比其他 Ο(nlogn) 算法更快,因为它的内部循环(inner loop)可以在大部分的架构上很有效率地被实现来。
时间复杂度: O(nlogn)
- n:每次分区函数的数组扫描
- logn:递归次数,”递归树“的高度
空间复杂度:递归调用次数 O(logn)
如图所示:递归调用次数平均情况下就是一个二叉树的高度logn
数组扫描O(n)
所以时间复杂度是O(nlogn),空间复杂度是O(logn)
四、注意事项
归并排序无论数据长啥样子,都是无脑的一分为二,保证递归次数一定是logn级别,非常稳定的nlogn的算法。
而快速排序的性能严格受制于初始数据的情况而定。
近乎有序的数组上,快速排序的性能退化非常的快。
关于分区点的选择问题:
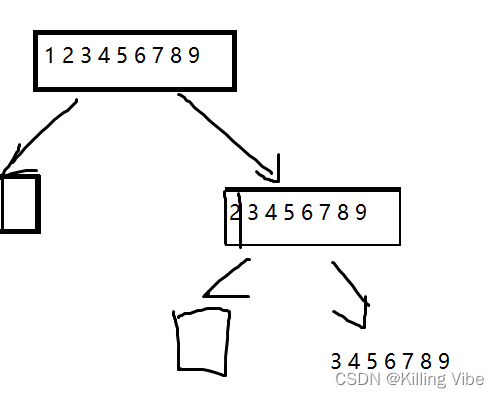
极端情况下,数组就是一个完全有序的数组
此时当数组近乎有序时,按照最左侧元素进行分区的时候,造成左右两颗递归树严重不平衡,甚至极端情况下退化为链表
空间:O( ) -> O( )
时间: =>
分区值的选择不能武断的就选择最左侧或者最右侧
a. 三数取中 =》 最左侧,最右侧,中间值 =》 选择其中之一
b. 每次递归时选择数组中任意一个元素作为分区点
优化:
关于分区点的选择。使用随机数随机取一个数组索引的元素作为分区点,基本上不可能出现单支树的情况,避免近乎有序数组上快排退化问题。

总结
以上就是快速排序的图解和代码,有什么疑问可以私信博主~有帮助的话可以关注博主后续更新。
- 点赞
- 收藏
- 关注作者


评论(0)