全排列笔记
46. 全排列
题目
给定一个 没有重复 数字的序列,返回其所有可能的全排列。
示例:
输入: [1,2,3]
输出:
[
[1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1]
]
解答
方法一:回溯
思路
从高中的数学知识我们可以知道
从[1,2,3]中选出3个数进行排列(排序有顺序之分、组合没有顺序之分)
结果有n!=3!=3*2*1种
1-2-3
1-3-2
2-1-3
2-3-1
3-1-2
3-2-1
怎么计算的呢?
假设现在我们有三个数:1、2、3
需要依次填入下面三个蓝色方块
那么第一个方块有三种选择:1或2或3
第二个有两种选择:2或者3(假设第一次选择了1)
那么第三个方块就只有一种选择:3(假设第一次选择1,第二次选择2)
综上:n个数(不重复),填入n个方块,一共有n!种不同排列方式。
那么为什么第一次有三种而第二次只有两种了呢?
这是因为第一次选择时,没有一个数被选,那么一个三个数,就有三种选择方法
到第二次选择时,因为第一次必定选择了一个数,这时剩下的可供选择的数就只有2个,选择就只有两种了
到第三次选择时,因为前面两次已经选择了两个数,可供选择的数就只有一个,选择就只有一种了
从上面提取核心思想:
每次进行选择时,我们都是从一些尚未选择的数中选择出一个数字填充方块,然后将该数标记为已选择,再进行下一轮新的选择。
根据上述思想,画出下面思路图:
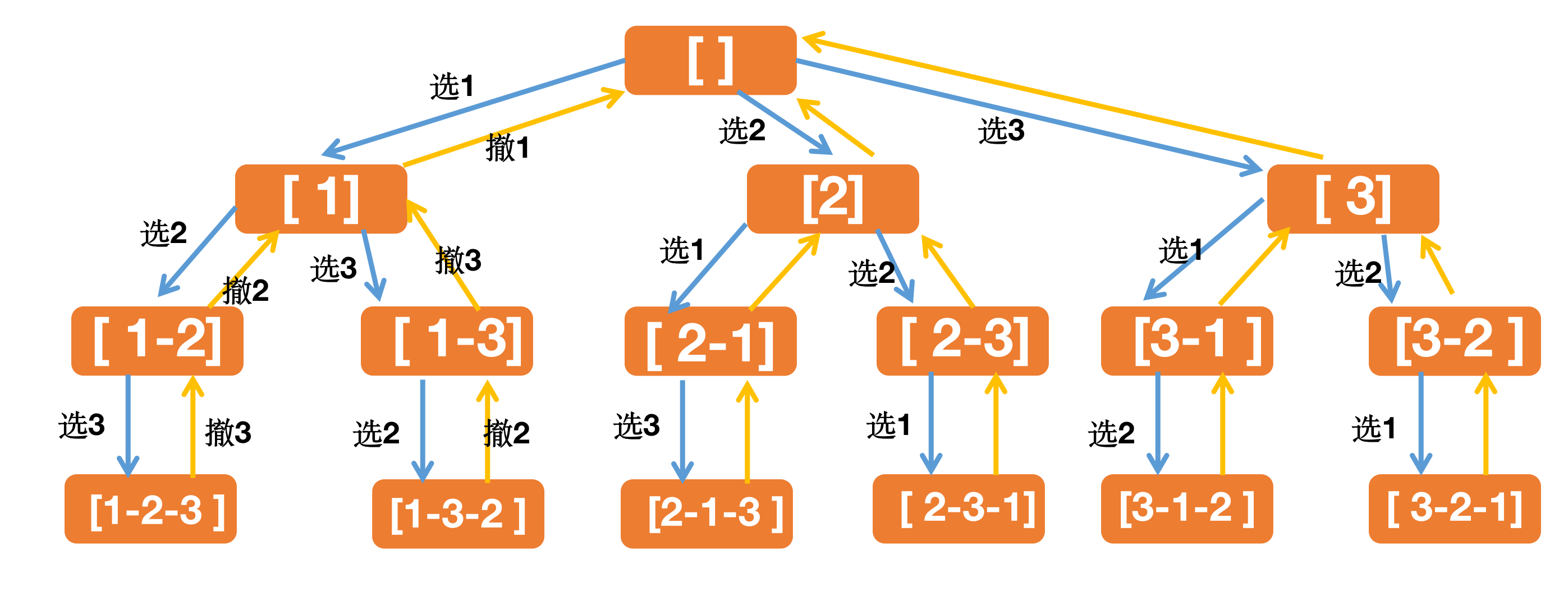
上图若没有理解 没有关系 先看下面
这里我们可以利用一个全局变量temp数组,初始化为空,作为一个临时容器
开始时,1、2、3都是尚未选择的
此时我们可以选择 1 或 2 或 3,有三种选择方法
假设我们选择了1后
那么将1添加至temp中【temp:1】
此时1已经被选择
之后可供我们选择的就是 2、3
再选择2【temp:1-2】
最后再选择3【temp:1-2-3】
此时temp与我们预期的答案吻合【其实就是temp数组的长度与预期结果数组长度一样】
将其添加至res结果数组中即可
在我们的思想中
可以很简单的知道 1被选择 2、3未被选择
但是在程序中,我们如何实现这个呢?
这里我们利用一个数组isused来判定元素是否被选择
假如情况是:1被选择 2、3未被选择
那么原数组与isused数组关系如下:
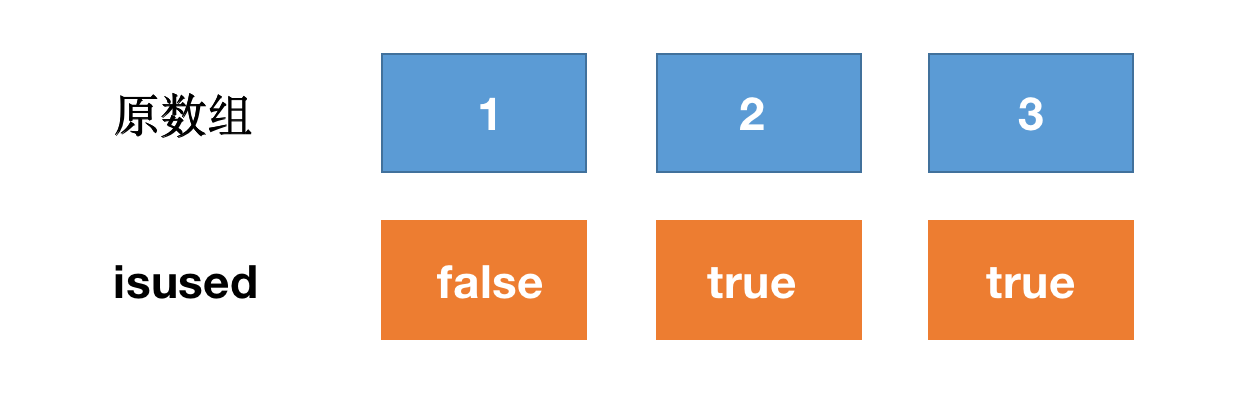
所以在每次进行选择前,我们利用isused数组,判定某个元素是否被选择
只有未被选择 我们才可以对这个元素进行操作
所以在每次选择前,我们都会扫描isused数组,当为true时,才对该元素进行操作。【具体是true还是false进行操作依据个人习惯而定,这里海轰是true代表未被选择】
根据上面的思路,写出下面的代码:
vector<int> temp;
void backtracking(vector<vector<int>> &res,vector<bool> &isused,vector<int> &nums){
// 当temp数组的长度等于期望数组的长度时 return
if(temp.size()==nums.size()){
res.push_back(temp);
return ;
}
// 遍历所有选择
for(int i=0;i<nums.size();++i){
// 对没有选择过的元素再进行抉择:选择它|不选择它
if(isused[i]){
// 选择该元素 选择后标记该元素为已选择 同时进行下一元素的抉择
temp.push_back(nums[i]);
isused[i]=false;
backtracking(res,isused,nums);
// 回复原来状态:未选择 同时从temp中pop出
isused[i]=true;
temp.pop_back();
}
}
}
vector<vector<int>> permute(vector<int>& nums) {
vector<vector<int> > res;
vector<bool> isused(nums.size(),true);
backtracking(res,isused,nums);
return res;
}运行结果

疑问
疑问1:程序具体是怎么执行的呢?
这里只给出程序的运行简图,
对详细步骤感兴趣对小伙伴可以自己动手画画步骤图
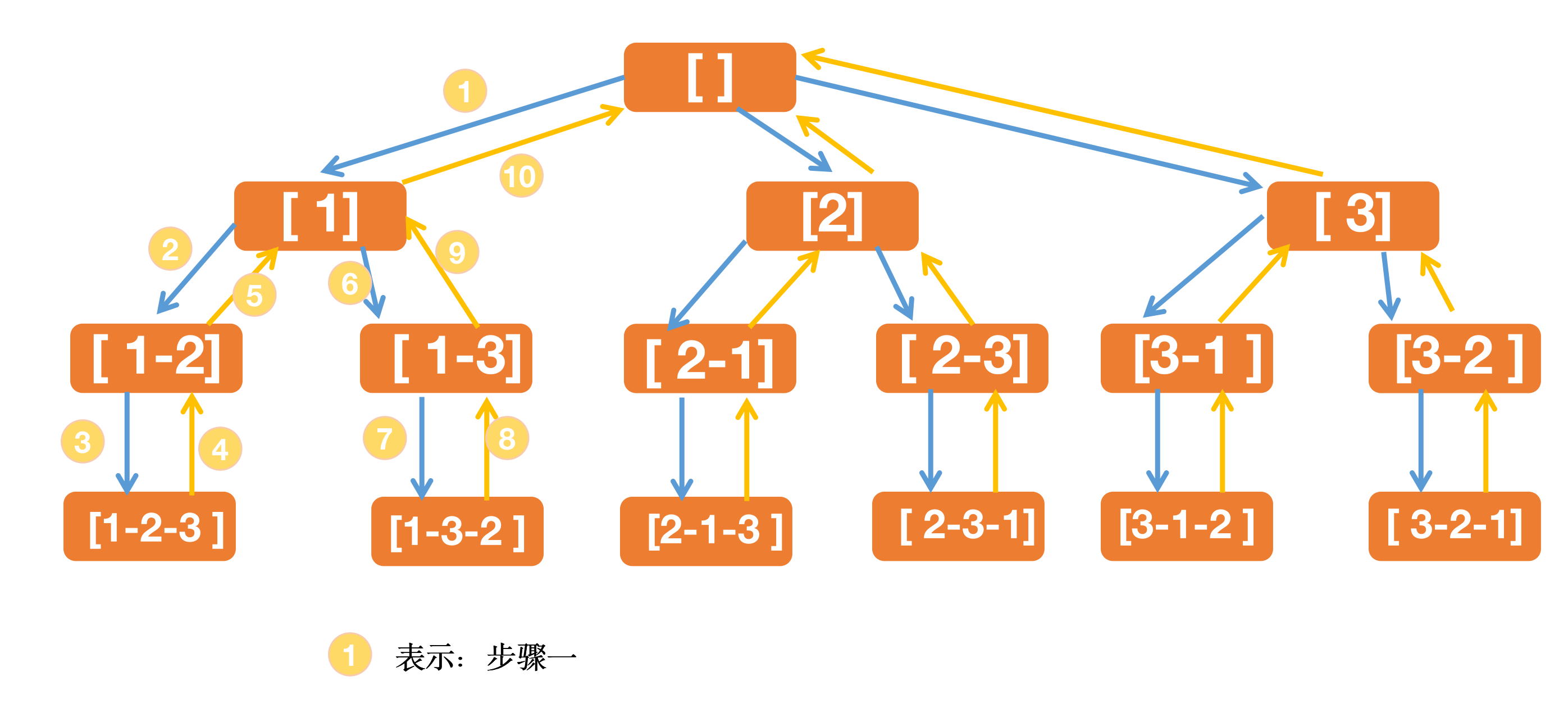
疑问2:为什么当 temp.size()==nums.size()或所有的元素都被选择后 函数backtracking返回呢?
首先
当temp.size()==nums.size()时
代表此时的temp已经满足答案需要
可以将其添加至res中
如果temp.size()<nums.size()
那么意思就是还temp中还需要一些元素
比如要求数组长度是4
此时temp长度只有2
那么就还需要再选择两个数进入temp
其次
当所有的元素都被选择后
说明已经没有元素可以供加入temp中
则必须return
疑问3:为什么 backtracking函数的开头就需要判定temp.size()==nums.size()?而不是在函数中部或者尾部?
首先可以看出
在这里我们用了递归
那么必须要一个递归终止条件
不然递归怎么结束呢?
backtracking作为一个递归函数
我们可以想到
每次进入backtracking函数时
第一要务就是需要判定此时temp的size
如果满足答案要求的长度
将temp压入res数组
再return
后面步骤也就不需要再运行
疑问4:为什么backtracking函数中每次要进行for(int i=0;i<nums.size();++i){}循环?
这里是因为每次进行抉择前
我们需要找出所有未被选择的元素
在这里我们使用的判定数组isused标志选择与否
所以每次都需要循环扫描isused数组【代码中:因为isused数组长度与nums数组一样,这里size写谁都可以】
疑问5:为什么会进行temp.pop_back()?
从代码中
我们可以发现
temp.pop_back()前面有句 backtracking(res,isused,nums,temp);
也就是说
只有backtracking(res,isused,nums,temp) 运行完后
才会进行temp.pop_back()
那么啥时候backtracking(res,isused,nums,temp)会结束呢?
参考疑问2
可以知道
backtracking(res,isused,nums,temp)结束时
代表某个元素已经被选择了,且引进被压入了temp中使用了
额外意思就是该元素已经被使用了
因为每次抉择都有两种:选择与不选择
那么选择结束了
之后肯定就是不选择了
但是此时元素已经被压入了temp中
那么需要怎么办呢?
简单,pop出即可,同时标记isuserd数组为true即可。
改进
改进方案:temp可以不定义为全局变量
代码如下:
void backtracking(vector<vector<int>> &res,vector<bool> &isused,vector<int> &nums,vector<int> &temp){
// 选择完毕
if(temp.size()==nums.size()){
res.push_back(temp);
return ;
}
for(int i=0;i<nums.size();++i){
if(isused[i]){
temp.push_back(nums[i]);
isused[i]=false;
backtracking(res,isused,nums,temp);
isused[i]=true;
temp.pop_back();
}
}
}
vector<vector<int>> permute(vector<int>& nums) {
vector<vector<int> > res;
vector<bool> isused(nums.size(),true);
vector<int> temp;
backtracking(res,isused,nums,temp);
return res;
}运行结果

改进方案:bool<->int push_back<->emplace_back
isused数组海轰使用的bool变量
在评论区有小伙伴说
当数据量大的时候使用int类型会好一点
同时
在将temp压入res时
使用emplace_back()会好一点
因为不会产生临时变量
代码如下:
vector<int> temp;
void backtracking(vector<vector<int>> &res,vector<int> &isused,vector<int> &nums){
// 当temp数组的长度等于期望数组的长度时 return
if(temp.size()==nums.size()){
res.emplace_back(temp);
return ;
}
// 遍历所有选择
for(int i=0;i<nums.size();++i){
// 对没有选择过的元素再进行抉择:选择它|不选择它
if(!isused[i]){
// 选择该元素 选择后标记该元素为已选择 同时进行下一元素的抉择
temp.push_back(nums[i]);
isused[i]=1;
backtracking(res,isused,nums);
// 回复原来状态:未选择 同时从temp中pop出
isused[i]=0;
temp.pop_back();
}
}
}
vector<vector<int>> permute(vector<int>& nums) {
vector<vector<int> > res;
vector<int> isused(nums.size());
backtracking(res,isused,nums);
return res;
}运行结果

方式二:回溯(官方题解,动态交换原数组中的元素)
官方题解代码如下:
void backtrack(vector<vector<int>>& res, vector<int>& output, int first, int len){
// 所有数都填完了
if (first == len) {
res.emplace_back(output);
for(int i=0;i<output.size();++i){
cout<<output[i]<<" ";
}
cout<<endl;
return;
}
for (int i = first; i < len; ++i) {
// 动态维护数组
swap(output[i], output[first]);
// 继续递归填下一个数
backtrack(res, output, first + 1, len);
// 撤销操作
swap(output[i], output[first]);
}
}
vector<vector<int>> permute(vector<int>& nums) {
vector<vector<int> > res;
backtrack(res, nums, 0, (int)nums.size());
return res;
}运行结果
思路
在官方题解中
并没有向我们使用的依次将元素添加至一个临时数组temp中
而是直接在原数组上进行变换
将变换结果依次加入结果数组res中。
程序具体执行过程如下:
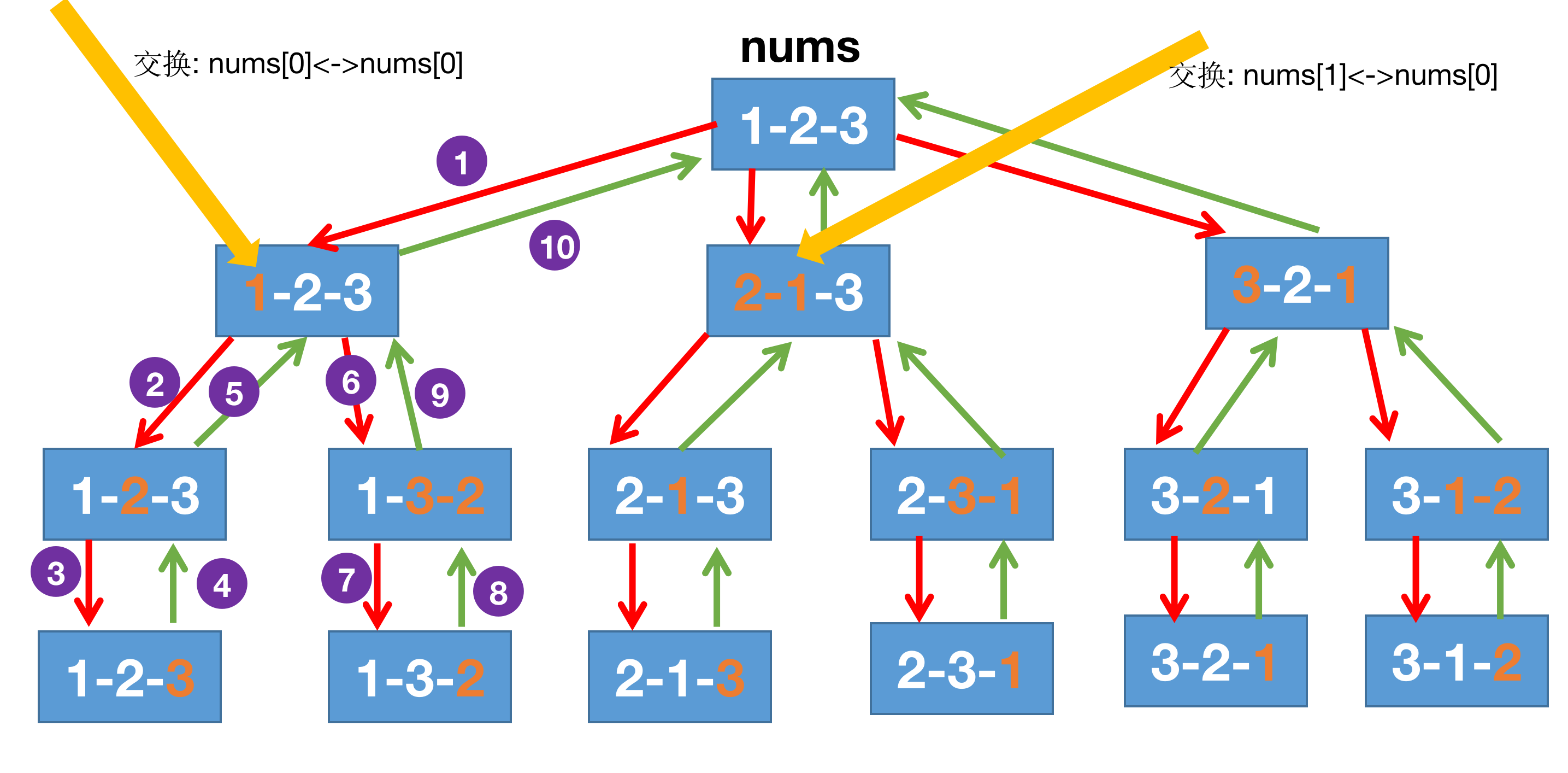
观察每个节点生成的下一个节点,元素是如何交换的?
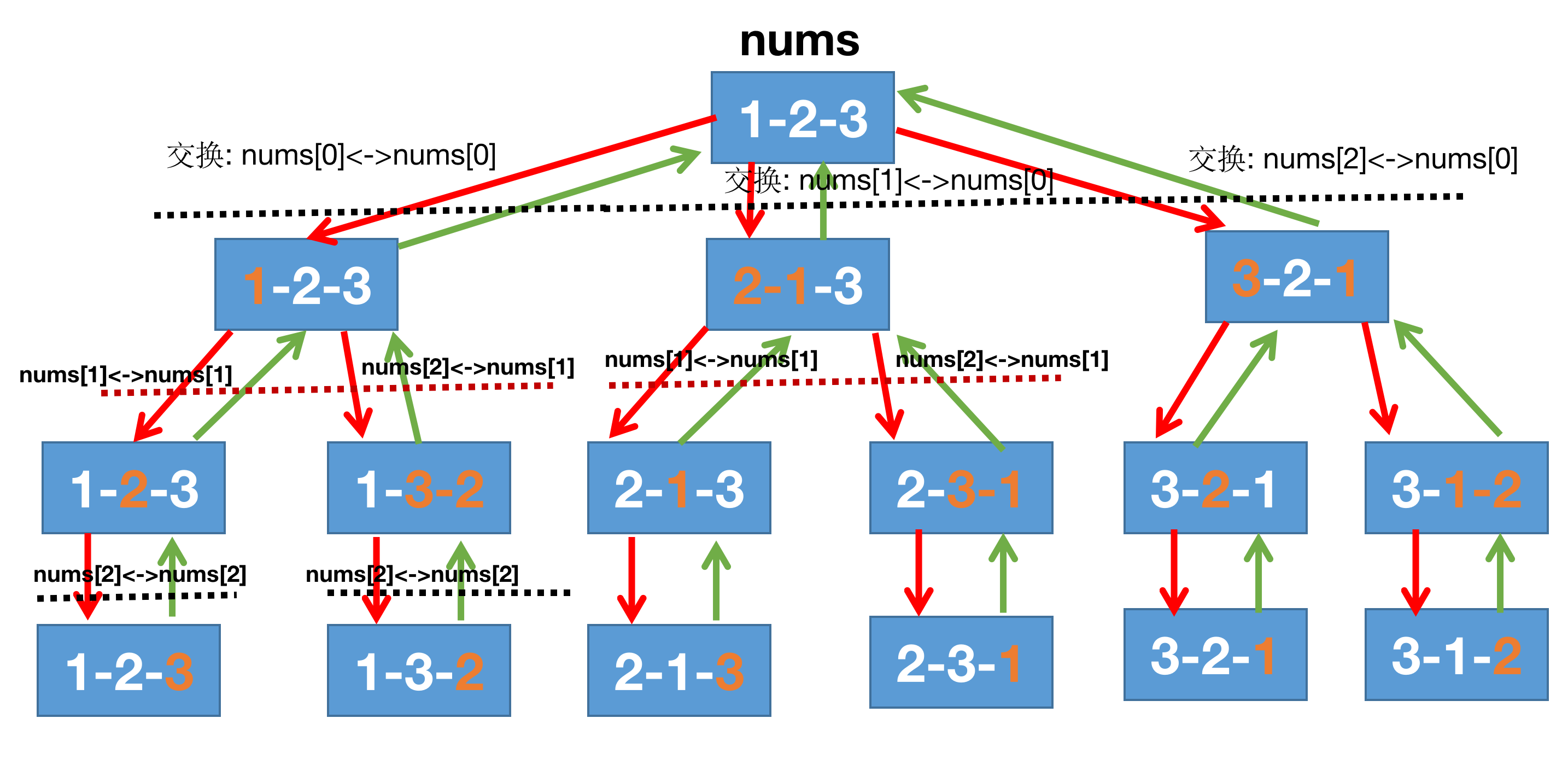
对for循环进行思考:
当first=0时,此时for循环会进行:swap(nums[0],nums[0])/swap(nums[1],nums[0])/swap(nums[2],nums[0])
当first=1时,此时for循环会进行:swap(nums[1],nums[1])/swap(nums[2],nums[1])
当first=2时,此时for循环会进行:swap(nums[2],nums[2])
for (int i = first; i < len; ++i) {
// 动态维护数组
swap(output[i], output[first]);
// 继续递归填下一个数
backtrack(res, output, first + 1, len);// 注意:这里是first+1
// 撤销操作
swap(output[i], output[first]);
}这里可能会有点难度
不好想象程序时如何进行的?
建议首先自己对照程序跑一次
明白每一次运行的结果
然后再对照上面几张图寻找规律
之后对官方题解就会有所理解了
变式
从[1,2,3,4,5,6]中,选择3个数进行排列,输出所有排列方式。
代码(修改backtracking函数中的返回条件即可)
vector<int> temp;
void backtracking(vector<vector<int>> &res,vector<bool> &isused,vector<int> &nums){
// 选择完毕
if(temp.size()==3){
res.push_back(temp);
return ;
}
for(int i=0;i<nums.size();++i){
if(isused[i]){
temp.push_back(nums[i]);
isused[i]=false;
backtracking(res,isused,nums);
isused[i]=true;
temp.pop_back();
}
}
}
vector<vector<int>> permute(vector<int>& nums) {
vector<vector<int> > res;
vector<bool> isused(nums.size(),true);
backtracking(res,isused,nums);
return res;
}运行结果

代码2(对官方题解进行修改):
void backtrack(vector<vector<int>>& res, vector<int>& output, int first, int len){
// 所有数都填完了
// 修改结束条件
if (first == 3) {
vector<int> temp(output.begin(),output.begin()+3);//利用临时数组存储
res.emplace_back(temp);
return;
}
for (int i = first; i < len; ++i) {
// 动态维护数组
swap(output[i], output[first]);
// 继续递归填下一个数
backtrack(res, output, first + 1, len);
// 撤销操作
swap(output[i], output[first]);
}
}
vector<vector<int>> permute(vector<int>& nums) {
vector<vector<int> > res;
backtrack(res, nums, 0, (int)nums.size());
return res;
}运行结果

- 点赞
- 收藏
- 关注作者


评论(0)