@TOC

简介

Hello！
非常感谢您阅读海轰的文章，倘若文中有错误的地方，欢迎您指出～
 
ଘ(੭ˊᵕˋ)੭
昵称：海轰
标签：程序猿｜C++选手｜学生
简介：因C语言结识编程，随后转入计算机专业，获得过国家奖学金，有幸在竞赛中拿过一些国奖、省奖…已保研
学习经验：扎实基础 + 多做笔记 + 多敲代码 + 多思考 + 学好英语！
 
唯有努力💪
 
【每日一读】每天浅读一篇论文，了解专业前沿知识，培养阅读习惯（阅读记录 仅供参考）

论文简介

原文链接：https://dl.acm.org/doi/10.1145/3394486.3403150

期刊：KDD '22: Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining （CCF A类）

年度：2022年8月20日（发表日期）

ABSTRACT

图卷积网络（GCN）通过有效地收集节点的局部特征取得了巨大的成功。然而，通常 GCN 更多地关注节点特征，而不是邻域内的图结构，尤其是高阶结构模式。然而，这种局部结构模式被证明是许多领域中节点属性的指示。此外，不仅仅是单一模式，所有这些模式的分布也很重要，因为网络很复杂，每个节点的邻域由各种节点和结构模式的混合组成。

相应地，在本文中，我们提出了 Graph Structuraltopic Neural Network，缩写为 GraphSTONE 1，这是一种利用图的主题模型的 GCN 模型，使得结构主题从概率方面广泛地捕获指示性图结构，而不仅仅是几个结构。

具体来说，我们使用匿名游走和 Graph Anchor LDA（一种首先选择重要结构模式的 LDA 变体）在图上构建主题模型，以减轻复杂性并有效地生成结构主题。

此外，我们设计了多视图 GCN 来统一节点特征和结构主题特征，并利用结构主题来指导聚合。我们通过定量和定性实验评估我们的模型，其中我们的模型表现出良好的性能、高效率和清晰的可解释性。

1 INTRODUCTION

Graphs2 由于其不规则性和稀疏性而难以处理。幸运的是，图卷积网络（GCN）成功地学习了图顶点的深度表示，并因其性能和可扩展性而引起了极大的关注。

虽然 GCN 成功地从节点的邻域中提取了局部特征，但应该注意的是，它们主要关注节点特征，因此不太能够利用节点的局部结构特性。具体来说，统一聚合描述了单跳关系，使得邻域内的高阶结构模式较少受到关注。此外，研究表明 [24] 深度 GCN 除了度数和连接组件外几乎无法学习，这进一步强调了这种无能。然而，节点的高阶局部结构模式，例如网络主题 [22] 确实为理解网络提供了深刻的指导。例如，在社交网络中，节点周围的网络主题将揭示社会关系 [6] 和动态行为 [30]。

在 GCN 中有几项利用高阶结构模式的工作，包括 [15]。然而，在[15]中，每个节点只选择了几个主题进行卷积，我们认为这是不够的。在大多数情况下，节点的高阶邻域由具有混合特征的节点组成，导致邻域内可能存在许多结构模式。因此，选择一些局部结构模式不足以完全表征节点的邻域。

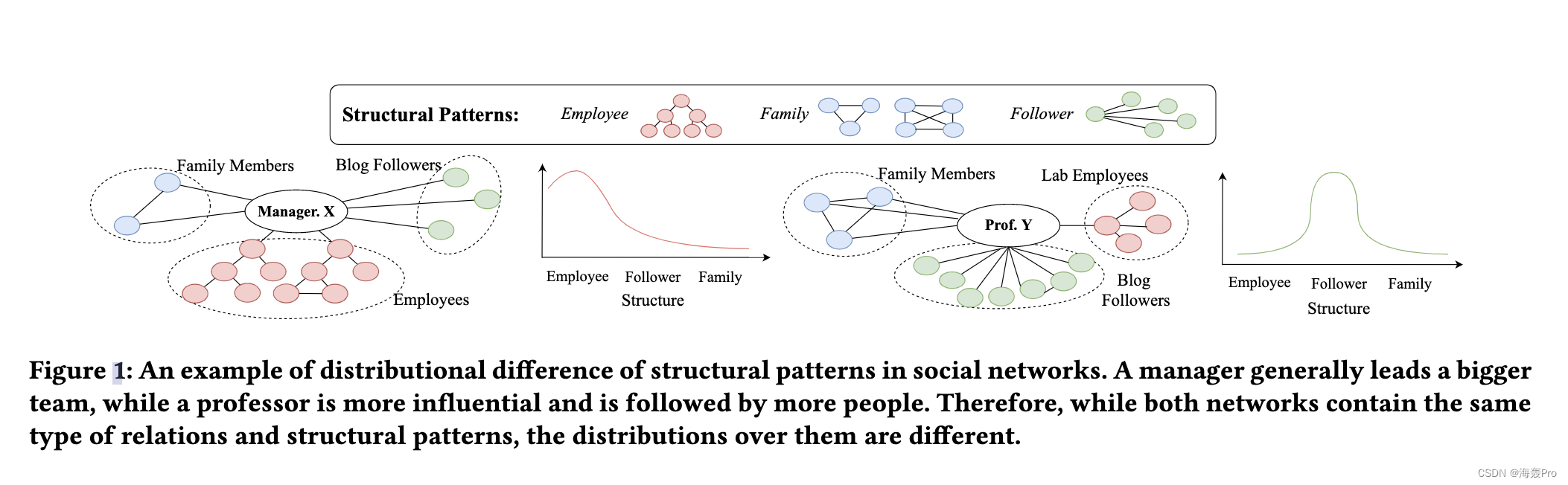
我们使用图 1 来说明我们的主张，该图显示了经理 X 和教授 Y 的社区，两者都具有三种类型的关系：家庭、员工和追随者。家庭成员相互了解，而员工形成等级制度，追随者可能高度分散，互不认识。可以看出，虽然两个网络都包含所有三种关系，但经理通常领导的团队更大，而教授的影响力更大，追随者也更多。因此，尽管星团、树木和恒星等结构模式出现在两个邻域中，但可以观察到它们的分布存在显着差异。因此，准确描述节点邻域需要的是结构模式的分布，而不是个体的分布。

---

主题建模是自然语言处理 (NLP) 中的一种技术，其中文档和主题都不是由个人定义的，而是主题和单词的分布。这种概率性质直接对应于描述复杂的高阶网络邻域所需的结构模式的分布。因此，我们类似地对具有结构主题的节点进行建模，以捕捉局部结构模式分布的这种差异。例如在图 1 中，以簇、树和星为特征的三个结构主题可以分别解释为家庭、员工和追随者，其中经理 X 和教授 Y 在结构主题上显示出不同的分布。

我们强调了图结构模式的主题模型的两个优点

• 一方面，概率建模更准确地捕捉节点局部结构模式的分布差异，更好地补充了 GCN 捕捉的节点特征。
• 另一方面，与以前直接处理高阶结构的工作相比，结构主题是低维表示[10]，因此具有较小的方差并提高了效率。

然而，在我们利用结构模式的主题建模来增强 GCN 的道路上，有几个主要障碍：

• 发现结构模式本身就很复杂。具体来说，以前的工作 [17] 通常专注于预定义的结构，这些结构可能不够灵活，无法很好地概括具有不同性质的网络。此外，许多结构指标需要模式匹配，其时间消耗对于 GCN 来说几乎是无法接受的。
• 图的主题建模也需要精心设计，因为图是关系的，而文档是独立的样本。因此，应进行适当的调整，以使结构主题在技术上是合理的。
• 在 GCN 中利用结构特征需要将节点特征与节点的结构特征统一起来。由于它们描述了节点的不同方面，因此需要精心设计图卷积，以便每组特征都可以作为另一组的补充。

为了应对这些挑战，在本文中，我们提出了图结构主题神经网络，缩写为 GraphSTONE，这是一个具有图结构主题建模的 GCN 框架。

具体来说，我们通过匿名游走 [21] 和 Graph Anchor LDA 对结构主题进行建模

• 一方面，匿名游走是一种描述结构模式的灵活有效的度量，它只涉及采样而不是匹配。
• 另一方面，我们提出了 Graph Anchor LDA，这是一种新的主题建模算法，它预先选择“锚”，即代表性的结构模式，这将在主题建模过程中得到强调。通过这样做，我们可以摆脱大量的结构模式，从而可以专注于相对较少的关键结构。因此，可以更高效地生成简洁的结构主题。

我们还设计了能够同时聚合节点特征和结构主题特征的多视图图卷积，并利用提取的结构主题来指导聚合。在多个数据集上进行了广泛的实验，我们的模型优于竞争基线。此外，我们对合成数据集进行了可视化，这提供了对 Graph Anchor LDA 和 GraphSTONE 的直观理解。

总而言之，我们做出以下贡献。

• 我们建议在图上进行结构主题建模，以捕获图上局部结构模式的分布差异，据我们所知，这是在图上利用主题建模的第一次尝试。
• 我们通过匿名游走和新颖的 Graph Anchor LDA 算法在图上进行主题建模，既灵活又高效
• 我们提出了一个多视图 GCN，将两个节点特征与结构主题特征统一起来，我们证明它们是相互补充的。
• 我们对多个数据集进行了广泛的实验，其中 GraphSTONE 在性能和效率方面都表现出了竞争力。

2 RELATED WORK

2.1 Graph Neural Networks (GNNs)

近年来见证了许多专注于图上的深度架构的工作 [7, 12]，其中 GCN 受到了最多的关注。 GCN 通常基于邻域聚合，其中节点的计算是通过对相邻节点的特征进行采样和聚合来进行的。

尽管邻域聚合使 GCN 与 Weisfeiler-Lehman (WL) 同构测试 [16, 23, 28] 一样强大，但常见的邻域聚合仅指节点特征，使其无法捕获复杂的邻域结构。这种弱点在理论上也有所体现。例如，[20] 指出 GCN 应该足够宽和足够深，以便能够检测给定的子图，而 [24] 表明深度 GCN 除了度数和连通分量外几乎不能学习。

作为补充，许多工作都集中在 GCNs 上，重点是高阶局部结构模式。

例如，

• [15] 在应用注意力之前选择邻域内的指示性主题，我们声称这是不够的。相反，我们的工作侧重于结构上的分布而不是单个结构。
• [10]通过匿名游走捕获局部结构模式，可以捕获复杂结构但效率低下。相比之下，我们使用主题模型的解决方案会更有效，因为我们为主题建模预先选择了锚点。

2.2 Modeling Graph Structures

以前有许多关于使用图元和最短路径等指标来描述图结构属性的工作 [4, 26]。但是，它们通常需要模式匹配，这在大型现实世界网络中难以承受。此外，这些模型受限于提取预先设计的结构模式，这些模式不够灵活，无法描述具有不同属性的现实世界网络。一个平行的工作线，如 [13] 旨在将图形分解为指示性结构。然而，他们专注于图级摘要，但未能生成节点级结构描述。

网络嵌入中的一些工作也利用网络结构来生成节点表示，例如 [5, 19, 25]。然而，它们的关注点通常是单一的，因为它们不涉及节点特征，而我们的模型能够通过 GCN 结合图结构和节点特征。

2.3 Topic Modeling

NLP 中的主题建模是一种广泛使用的技术，旨在对文本进行聚类。此类模型为每个文档分配主题分布，并为每个主题分配单词分布，以提供文档和单词的低维概率描述。

潜在狄利克雷分配（LDA）[3]，一个三级生成模型，体现了最典型的主题模型。然而，尽管在 NLP [11, 18] 中很普遍，LDA 几乎没有（如果有的话）被用于非独立同分布。网络等数据。在这项工作中，我们设计了一个关于网络的主题模型，其中引入了结构主题以捕捉网络中结构模式的分布差异。

3 MODEL: GRAPHSTONE

在本节中，我们介绍我们的模型 Graph Structural-topic Neural Network，即 GraphSTONE。在介绍多视图图卷积之前，我们首先介绍图上的主题建模。

图 2 概述了我们的模型 GraphSTONE。对每个节点进行匿名随机游走以描述节点的局部结构。然后在每个节点的匿名游走上执行图锚 LDA，我们首先选择“锚”，即通过非负矩阵分解的指示性匿名游走。在获得 walk-topic 和 node-topic 分布后，我们通过多视图 GCN 将这些结构属性与原始节点特征相结合，该 GCN 输出每个节点的表示。

3.1 Topic Modeling for Graphs

3.1.1 Anonymous Walks

我们在这里简要介绍匿名行走，并请读者参考 [8, 21] 了解更多详细信息。

匿名漫步与随机漫步类似，但去掉了节点的确切身份。匿名行走中的节点由它出现的第一个位置表示。图2 (a)提供了我们认为有吸引力的匿名行走的直观解释。例如，𝑤𝑖=(0,9,8,11,9)是从节点0开始的随机游走，其匿名游走定义为𝑤𝑖=(0,1,2,3,1)，极有可能是通过三元闭包生成的。

我们提出以下定理来证明匿名游走在描述图结构中的性质。

定理1。[21]让𝐵(𝑣𝑟)是所有节点引起的子图𝑢这样𝑑𝑖𝑠𝑡(𝑣𝑢)≤𝑟和𝑃𝐿是匿名的长度的分布𝐿从𝑣开始,我们可以重建𝐵(𝑣𝑟)使用(𝑃1,……,𝑃𝐿),𝐿= 2(𝑚+ 1),𝑚边的数量在𝐵(𝑣𝑟)。

定理 1 强调了匿名游走以一般方式描述节点的局部结构的能力。因此，我们将每个匿名游走作为描述图结构的基本模式3。

3.1.2 Problem Formulation

我们在我们的论文中制定了关于图的主题建模如下。

定义1(图的主题建模)。给定一个图𝐺=(𝑉，𝐸)，一组长度为𝑙的可能匿名行走作为W𝑙，以及所需结构主题的数量𝐾，图上的主题模型旨在学习以下参数。

• 一个节点主题矩阵𝑅∈R|𝑉|×𝐾，其中行𝑅𝑖对应一个分布，其中𝑅𝑖𝑘表示节点𝑣𝑖属于𝑘-th结构主题的概率。
• 一个步行主题矩阵𝑈∈R𝐾× | W𝑙|，其中行𝑈𝑘是W𝑙的分布，𝑈𝑘𝑤表示𝑤∈W𝑙属于𝑘-th结构topic.topic的概率。

此外，我们定义了从𝑣𝑖as𝐷𝑖开始的匿名步行集合，并使用𝐷𝑖=𝑁作为要采样的步行数。

该公式类似于 NLP 中的主题建模，其中匿名游走对应于单词，从每个节点开始的游走集合对应于文档。通过进行类比，节点被给出了对其局部结构模式的概率描述，因此结构主题将由指示节点属性的结构模式分布组成（例如，图 1 中的社会关系）。

根据 NLP [2] 中的 LDA 约束，我们引入引理 1 来证明网络中的主题模型确实可以学习。

引理1。如果𝑁和步行长度𝑙满足条件，有一个多项式时间算法可以在误差为𝜖的图上适合主题模型

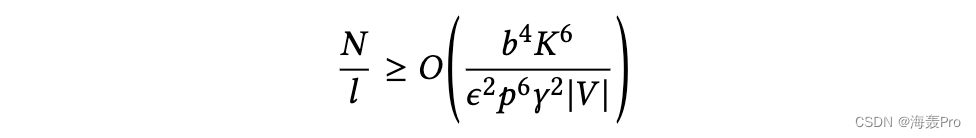
其中𝐾为主题数，|𝑉|为节点数。𝑏、𝛾和𝑝是与[3]中定义的主题不平衡相关的参数，我们假设它是固定的。

首先介绍引理的一般思想。在NLP的主题模型中，假设每个文档|𝐷𝑖|的长度和词汇表W是固定的，而语料库|D |是可变大小的。图中存在明显的差异，其中节点|D | = |𝑉|的数量是固定的，而匿名行走集和样本的大小是可变的。因此我们关注𝑁，𝑙而不是|D |。

证据。[2]给出了一个文档数量的下界，使得主题模型可以匹配，即

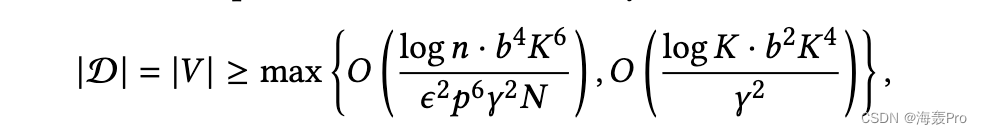
其中𝑛= |W𝑙|是词汇量。由于后一项是常数，我们关注第一项。

我们得到𝑁和|W𝑙|的界，即

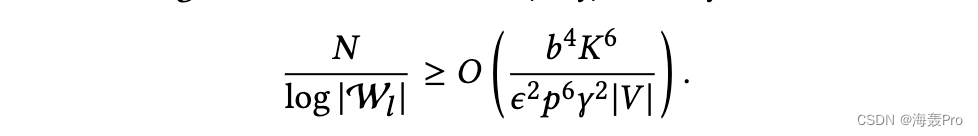
匿名步行的数量随步行的长度呈指数增长𝑙[8]，即。

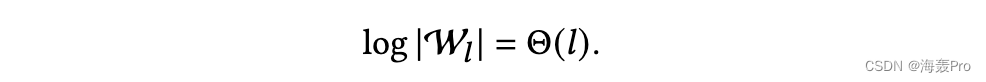
因此，我们得到引理1。

3.1.3 Graph Anchor LDA

在复杂的网络上会产生大量不同的行走序列，其中许多可能不是指示性的，如[22]所示。如果将序列分开考虑，我们将会遇到巨大的“词汇表”，这将损害我们的模型，因为该模型可能会过度适合无意义的序列，而忽略更重要的序列。

不幸的是，虽然在NLP中，停用词的概念被用来删除无意义的单词，但在网络中不存在这样的结果来删除这样的行走序列。因此，我们建议在进行进一步的主题建模之前，首先选择高度指示性的结构，我们称之为“锚”。

具体来说,我们定义walk-walk同现矩阵𝑀∈R W𝑙| |×| W𝑙|,与𝑀𝑖,𝑗=我𝑣𝑘∈𝑉我(𝑤𝑖∈𝐷𝑘,𝑤𝑗∈𝐷𝑘),并采用非负矩阵分解(NMF)[14]提取锚

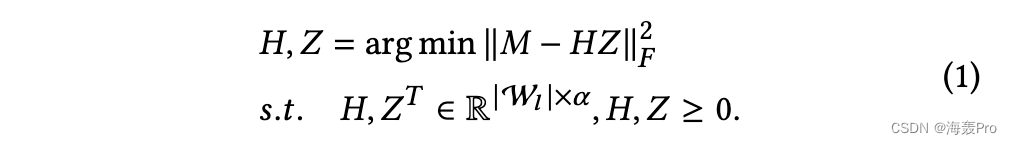
我们迭代更新𝐻，𝑍直到收敛，然后通过A找到锚𝑘= arg max(𝑍𝑘)，𝑘= 1，…𝛼，其中A是锚的索引集，𝑍𝑘是𝑍的𝑘-th行。直观地说，通过选择权重最大的步法，我们就是在选择最能解释其他步法发生情况的步法，即指示性步法。我们随后从理论上表明，所选步行不仅表明步行的共同发生，而且还表明潜在的主题。

基于我们选择的锚点，我们继续学习步行主题分布𝑈。[1]提出了一种以锚点为主要指标，非锚点提供辅助信息的LDA快速优化方法。通过优化得到𝑈∈R𝐾× | W𝑙|

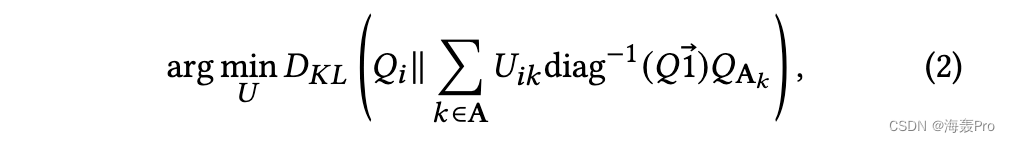
其中𝑄是重新排列的行走共现矩阵，其中anchorsA位于前𝛼行和列中，𝑄A𝑘是𝑘-th锚的𝑄for行。

我们定义节点行走矩阵𝑌∈R|𝑉|× | W𝑙|，其中𝑌𝑖𝑤表示𝑤在𝐷𝑖中的出现次数。然后我们得到节点主题分布𝑅到𝑅=𝑌𝑈†，其中𝑈†表示伪逆。

3.1.4 Theoretical Analysis.

在这里，我们提供了一个简短的理论分析，我们的图形锚LDA的能力，恢复“锚”不仅行走共现，而且主题。我们首先通过可分矩阵的定义来形式化“锚”的概念。

定义2(𝑝-separable矩阵)。[2]一个𝑛𝑟非负矩阵𝐶𝑝-separable如果每个𝑖有行𝜋𝐶(𝑖),只有一个非零项𝐶𝜋(𝑖),与𝐶𝑖𝜋(𝑖)𝑖≥𝑝。

具体来说，如果行走主题矩阵𝑈是可分离的，我们将具有非零权重的行走称为“锚”。然后，我们从[2]推导出一个推论，表明非负矩阵分解确实能够找到这样的锚。

推论1。假设真实步行节点矩阵(即每个节点的真实步行分布)通过𝑌=𝑈Λ生成，其中𝑈Λ是真实步行主题矩阵，Λ是系数矩阵，都是非负的。我们定义Σ= E[𝑌𝑌𝑇]= E[𝑈ΛΛ𝑇𝑈𝑇]和ˆΣΣ的观察。对于每一个𝜀> 0，都有一个多项式时间算法，它分解出Σ≈，使得∥∥1≤𝜀。此外，如果𝑈是𝑝-separable，那么在错误为𝑂(𝜀)之前，口令口令𝑈的行几乎会重构锚。

具体地说，行走共现矩阵𝑀作为推论1中行走协方差Σ的估计Σ。推论1强调，我们的Graph Anchor LDA算法确实能够在每个结构化主题中选择具有代表性的结构模式。在现实中，话题通常是不可分离的，我们将实证证明主播选择的有效性。

3.1.5 Discussion.

我们讨论了图锚点LDA和社区检测的区别，这两种方法都可以用于图的降维。虽然社区检测关注的是密集连接，但Graph Anchor LDA关注的是局部结构的分布，这将把相似的主题分配给结构相似但不一定相连的节点(例如？然后呢？图3)。在实验中，我们将通过比较Graph Anchor LDA和MNMF[9]来显示这种差异。

3.2 Structural-topic Aware GCN

然后我们介绍了我们的图卷积的设计，它融合了结构主题特征和节点特征。

3.2.1 Structural-topic Aware Aggregator

目前流行的GCN算法聚集了所有具有相同贡献的邻居，而GAT虽然给邻居分配了不同的权重，但只考虑了节点特征，而没有考虑结构属性。因此，我们建议利用学习到的结构主题来指导邻居的聚合。我们利用基于结构主题相似性的节点重要性抽样方案，使得邻域可以以一种说明同质性的方式聚集，即相似的节点彼此影响更大，

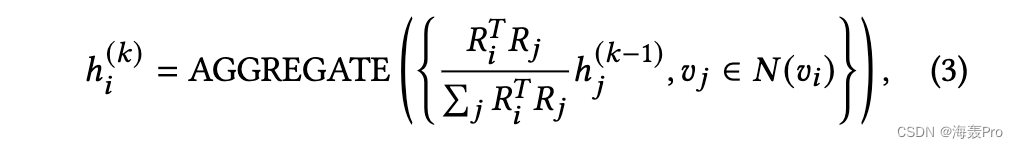
其中ℎ(𝑘)𝑖表示来自𝑘-th层的节点𝑣𝑖的输出向量。我们采用与GraphSAGE相同的AGGREGATE，同时对更复杂的方法具有灵活性。

3.2.2 Multi-view GCN

由于这两种类型的功能来自不同的领域，因此利用一种功能来补充另一种功能是理想的。受到提升思想的启发，我们引入了两个并行的GCNs，一个专注于结构主题，另一个相应地关注节点特征。具体地说,让ℎ(𝑘)𝑖𝑛和ℎ𝑘𝑖,𝑠𝑘= 1,…，𝐿denote为节点𝑣𝑖在𝑘层的两个GCNs的输出，我们在两个输出向量上应用非线性神经网络层。

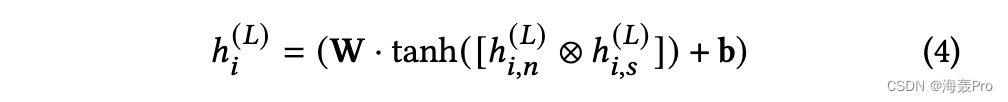
其中ℎ(𝐿)𝑖是节点𝑣𝑖的多视图GCN的最终输出，而⊗可以是任意操作，我们将其作为连接。

ℎ的初始化(0)𝑖,我们把ℎ(0)𝑖𝑛=𝑋𝑖,节点的特征𝑣𝑖,和ℎ(0)𝑖𝑠是下面的连接:a)锚的向量表示分布在附近的𝑣𝑖,和b) node-topic分布𝑅𝑖。

最后，我们采用GraphSAGE[7]的无监督目标学习输出向量。

其中𝜎(𝑥)是sigmoid函数，𝑣𝑗与𝑣𝑖在随机漫步中共出现，𝑃𝑛(𝑣)是负抽样的噪声分布。

我们在算法1中给出了GraphSTONE的伪代码。

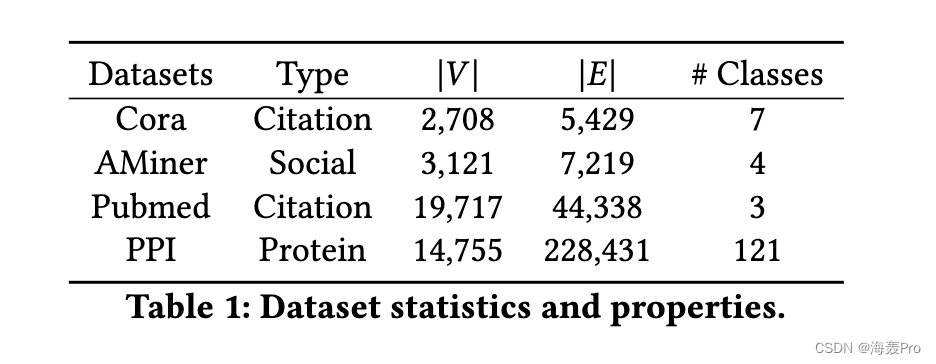
4 EXPERIMENTS

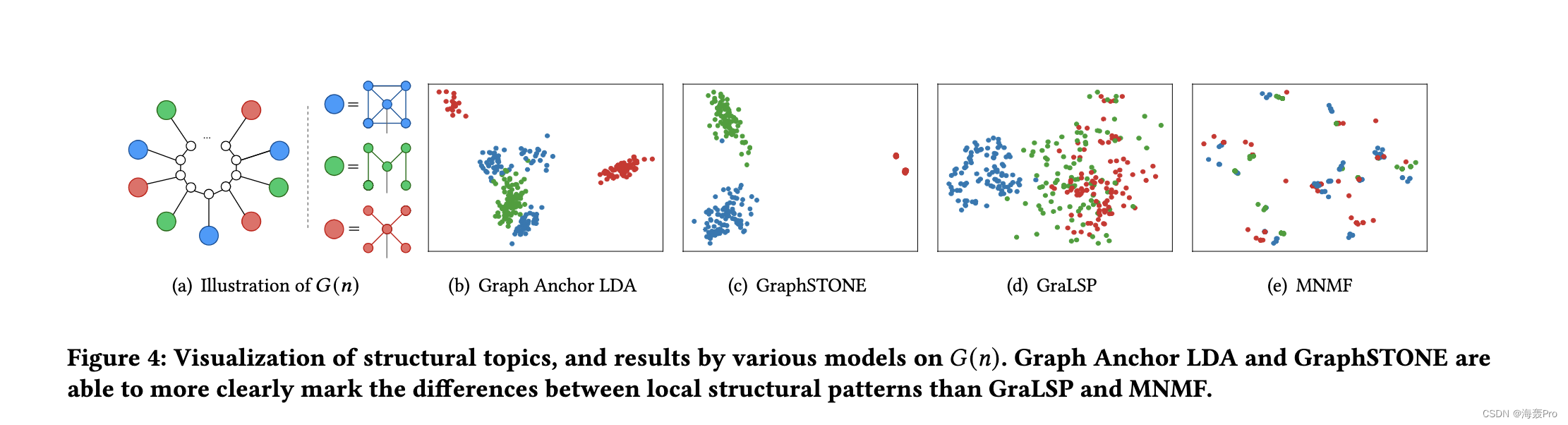
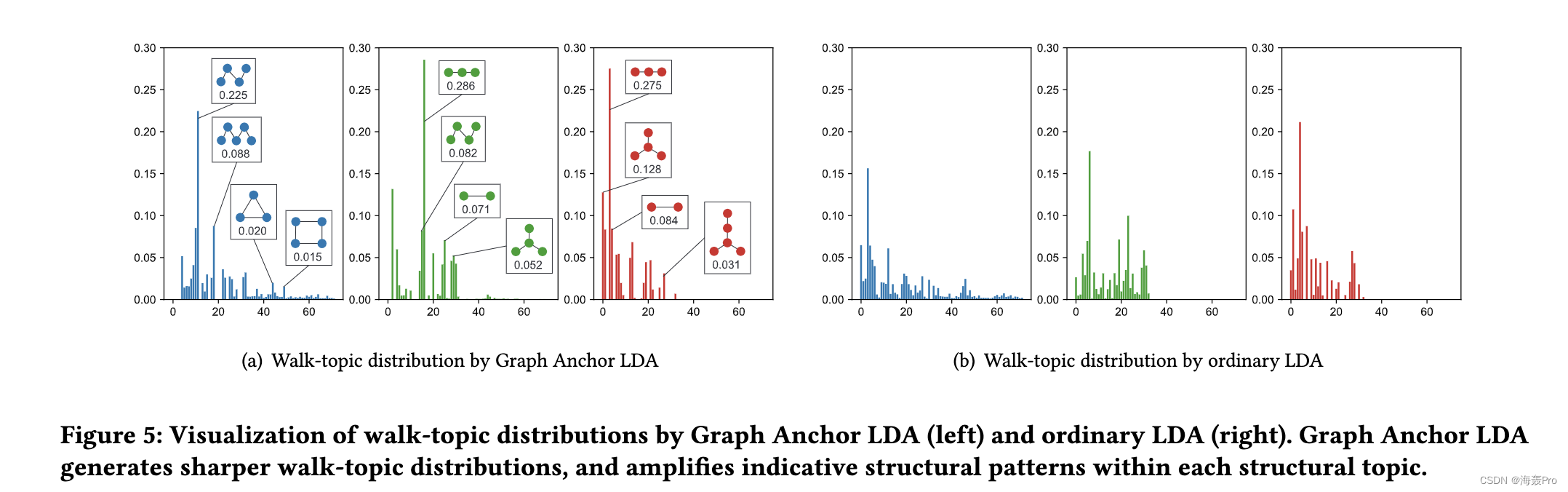
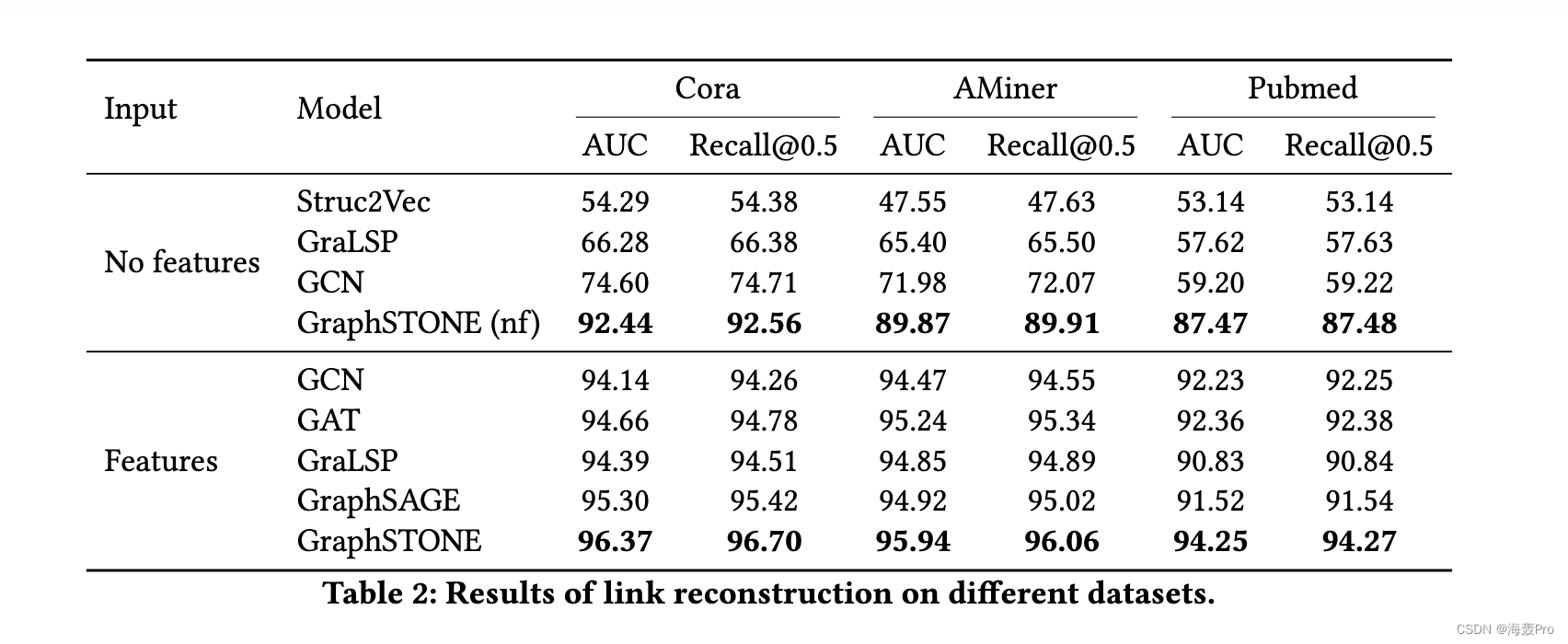
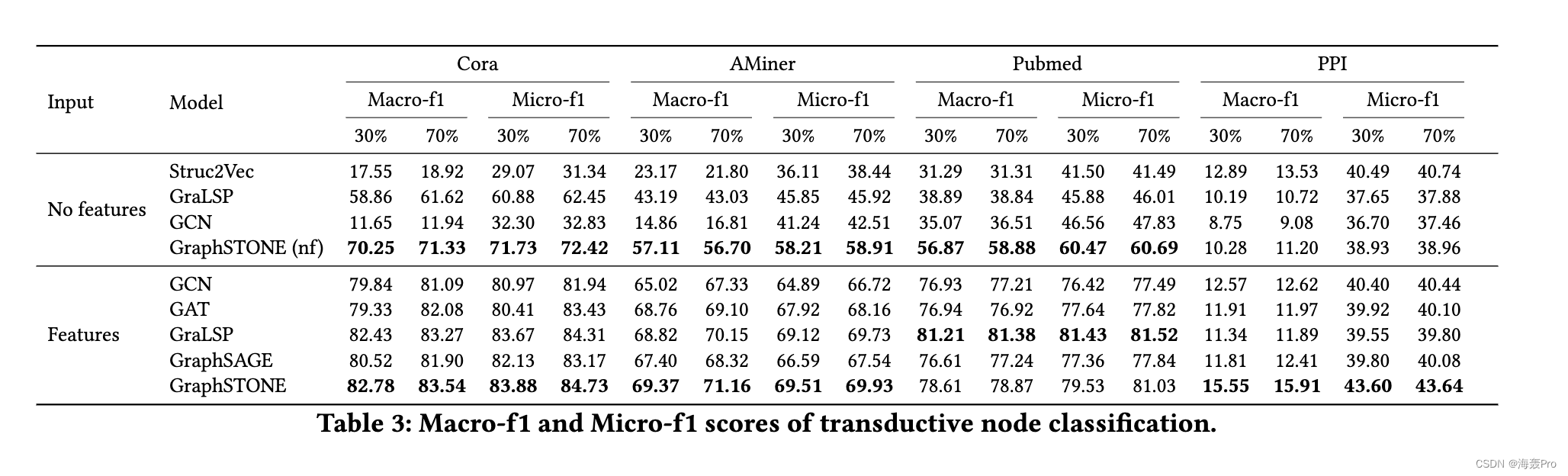
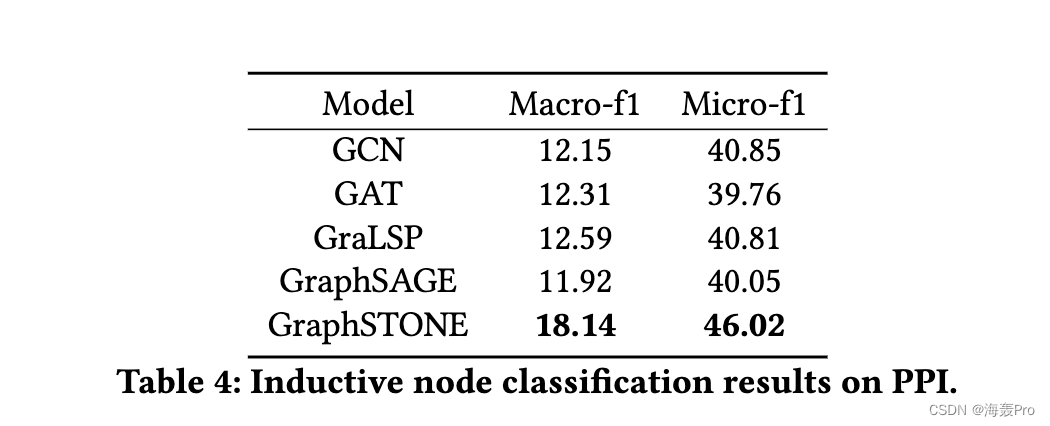
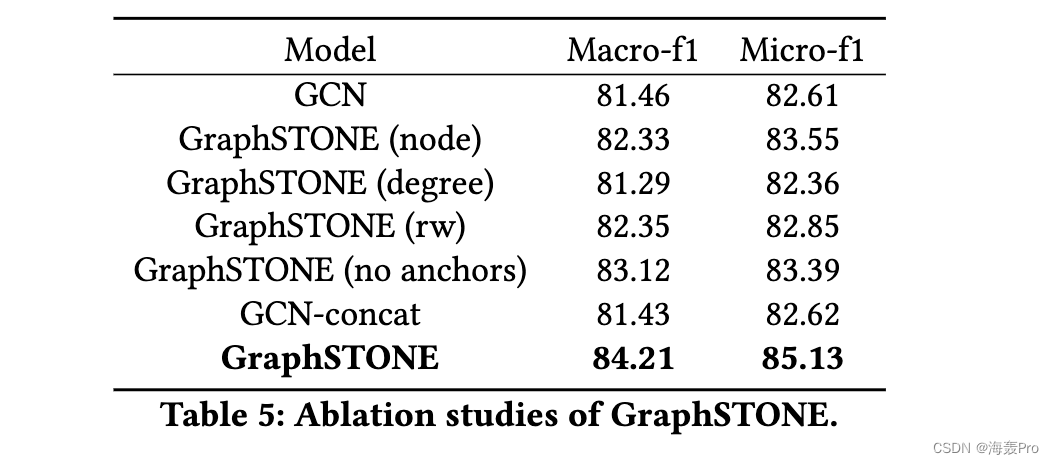
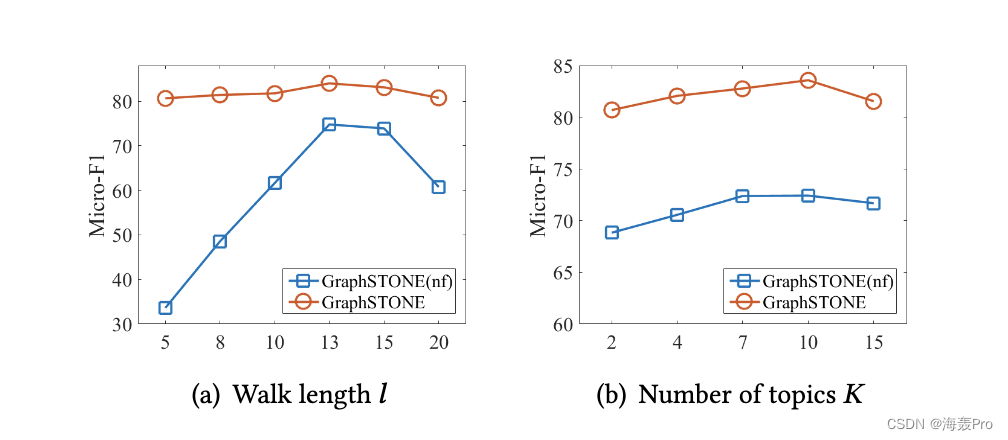
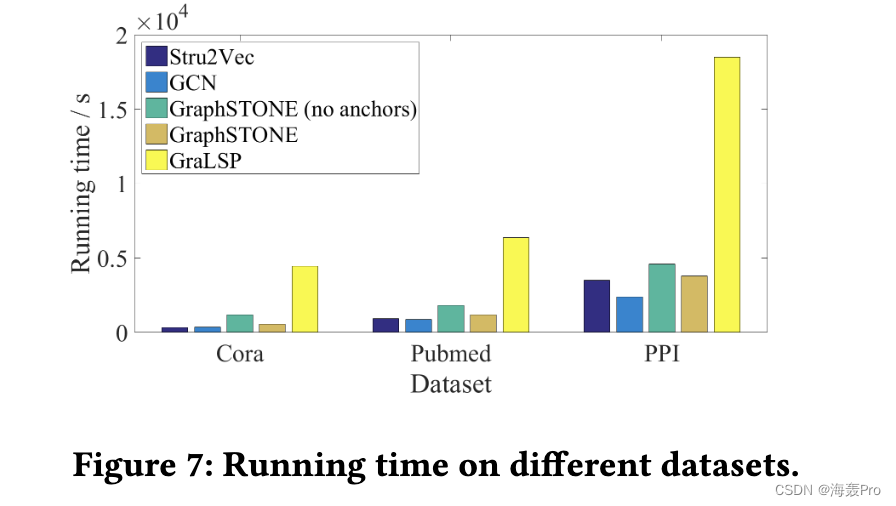
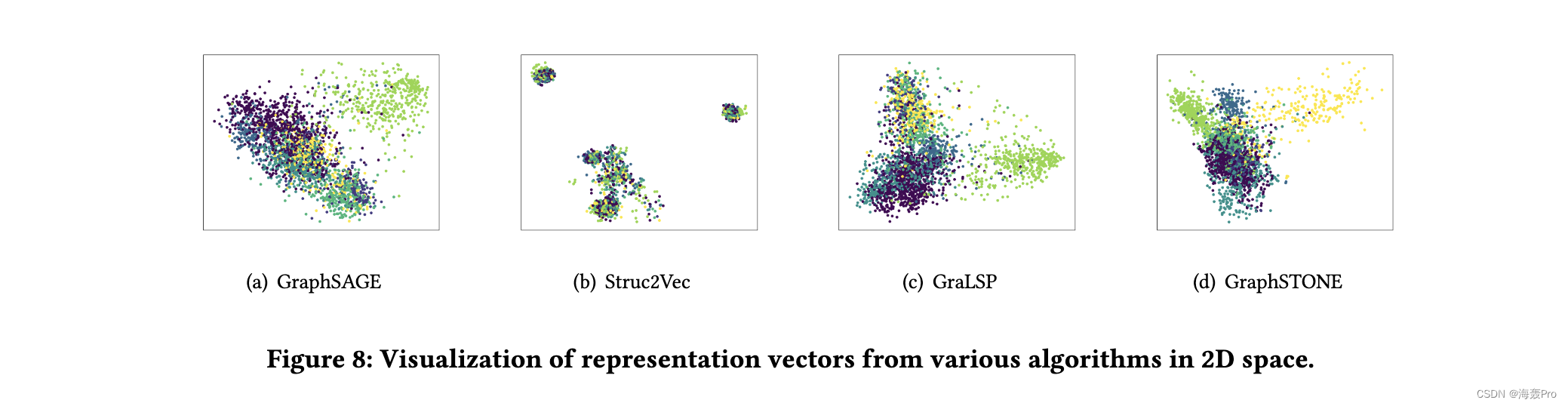
5 CONCLUSION

在本文中，我们提出了一种GCN框架，该框架捕获用于图卷积的局部结构模式，称为GraphSTONE。

据我们所知，这是在图和GCN上进行主题建模的第一次尝试。

具体地说，我们观察到局部结构模式的分布而不是个体指示网络中的节点属性，而当前的GCN几乎不能建模。

然后，我们利用主题建模，特别是Graph Anchor LDA来捕捉局部结构模式上的分布差异，并使用多视图GCN来结合这些属性。

我们通过多个实验证明了GraphSTONE是具有竞争力、高效和可解释的。

在未来的工作中，我们试图扩展我们的工作，看看GNN如何通过结合各种图结构在理论上得到改进。

结语

文章仅作为个人学习笔记记录，记录从0到1的一个过程

希望对您有一点点帮助，如有错误欢迎小伙伴指正