@TOC

简介

Hello！
非常感谢您阅读海轰的文章，倘若文中有错误的地方，欢迎您指出～
 
ଘ(੭ˊᵕˋ)੭
昵称：海轰
标签：程序猿｜C++选手｜学生
简介：因C语言结识编程，随后转入计算机专业，获得过国家奖学金，有幸在竞赛中拿过一些国奖、省奖…已保研
学习经验：扎实基础 + 多做笔记 + 多敲代码 + 多思考 + 学好英语！
 
唯有努力💪
 
【每日一读】每天浅读一篇论文，了解专业前沿知识，培养阅读习惯（阅读记录 仅供参考）

论文简介

原文链接：https://dl.acm.org/doi/10.1145/3473911

期刊：TKDD （CCF B类）

代码：https://github.com/larry2020626/LEMON

年度：2021年10月22日（发表日期）

Abstract

网络嵌入已经成为处理下游任务的有效方法，例如节点分类 [16,31,42]。大多数现有方法利用节点之间的多重相似性，例如连接性，它认为紧密连接的顶点是相似的，结构相似性是通过评估它们与邻居的关系来衡量的；而这些方法只关注静态图。

在这项工作中，我们通过基序以统一的表示形式连接连通性和结构相似性，并因此提出了一种通过利用网络基序 (LEMON) 来学习嵌入的算法，该算法旨在学习顶点和各种基序的嵌入。

此外，LEMON 天生就能够处理动态图的归纳学习任务。为了验证有效性和效率，我们对来自不同领域的两个真实数据集和五个公共数据集进行了各种实验。通过与最先进的基线模型进行比较，我们发现 LEMON 在下游任务上取得了显着的改进。

1 INTRODUCTION

图表是一种有效且自然的方式来表示来自各种领域（如社交网络和学术网络）的数据。图结构可以是多种多样且不规则的，因为图的大小是可变的，无序的顶点可能有或多或少的邻居[49]。图嵌入，也称为网络嵌入，旨在学习顶点的表示，已经成为许多下游应用的有效方法，例如节点分类、链接预测等 [16,31,42]。

许多算法采用随机游走来生成语料库，然后将其输入 Skip-gram 模型 [27] 以学习潜在嵌入。基本概念涉及自动将给定网络的顶点投影到低维潜在空间中，其中相似的顶点彼此靠近。一个关键问题是如何定义最适合下游应用程序的顶点相似度度量。文献中的先前工作考虑了不同的顶点相似性度量，例如连通性和结构相似性。连通性认为紧密连接或具有许多共同邻居的顶点彼此相似[16、31、42]；另一方面，结构相似性衡量两个顶点是否共享相似的局部结构[34]。一些现有的工作试图考虑多种相似性，例如，VERSE [45] 提出了三个相似性：社区结构、角色和结构对等。值得注意的是，社区结构实质上等于连通性（节点连接或有许多共同邻居），而结构相似性可以涵盖角色和结构对等。 对于现实世界的数据集，研究人员通常会遇到动态场景：在电信数据集中，用户之间是动态调用的；在学术网络中，形成合作并不断发表新论文。然而，据我们所知，上述大多数方法仅从一种相似性的角度学习顶点的表示。此外，大多数现有方法都不适合为看不见的顶点生成嵌入。

一些现有的工作已经专注于归纳学习任务，例如 GraphSAGE [17]，它通过聚合来自邻域的特征来表示顶点。但是，仅从邻居聚合特征仅考虑连通性可能会在重视结构属性的任务中失败。以电信欺诈检测为例，欺诈行为与普通用户不同，这可以通过异常的结构模式来反映[52]。因此，上述方法不适用于重视结构相似性且不足以捕捉复杂现实世界数据集的综合特征的数据集。因此，我们建议研究一个问题：我们如何在统一表示中同时测量连通性和结构相似性，同时能够处理归纳学习任务？

作为网络的基本构建块[28]，motif 描述了在顶点之间具有特定连接的小子图模式，它表示结构并包含内部顶点的连接信息。主题在包括生物信息学、神经科学、生物学和社交网络在内的一系列领域中是有效且至关重要的[54]。

图 1 说明了不同网络中的三角形图案

• 在社交网络中，三个亲密的朋友形成一个三角形母题（ ）；
• 在学术网络中，三位经常合作发表论文的学者组成了另一位学者。

Motifs包含丰富的信息，可以揭示顶点的语义信息；例如，在社交网络中，带有几个 ( ) 的顶点代表一个倾向于介绍她的朋友认识彼此的人，与被 ( ) 包围的顶点形成对比。一些现有的作品试图通过主题 [22, 40, 58] 生成嵌入。据我们所知，这些方法中的大多数只关注静态图的节点嵌入。

鉴于上述情况，为了解决这些问题，我们提出了一种通过主题考虑多重相似性来学习表示的方法。除了其他与主题相关的方法外，主要区别在于我们提出的方法明确提出主题作为超顶点，而不是在学习顶点表示时隐式利用主题来施加影响。此外，主题允许我们实施归纳学习方法；特别是，我们可以通过嵌入其相关主题的向量来有效地获得新顶点的表示。在这篇文章中，我们提出了一个新的算法框架：Learning Embeddings based on Motifs Of the Network (LEMON)。

LEMON将各种motifs作为超顶点放入网络中，构建了一个由motif超顶点与网络中原始顶点之间的关系组成的异构网络。此外，为了将异构网络整合到 Skip-gram 模型 [27] 中，我们提出了一种主题步随机游走策略，以确保具有高连通性或高结构相似性的顶点将在语料库中紧密地出现。因此，我们的框架能够同时测量连通性和结构相似性。我们文章的主要贡献可以总结如下：

• 我们建议通过测量连通性和结构相似性来研究统一学习网络嵌入的问题。
• 我们提出了一个名为 LEMON 的新框架，它利用主题超顶点生成顶点和主题的嵌入，并可应用于归纳学习任务。
• 我们使用两个真实世界的数据集和五个公共数据集来评估我们提出的框架在四个不同任务上的有效性和效率。实验结果表明，LEMON 的性能优于 11 个最先进的基线模型。

2 PRELIMINARIES

2.1 Problem Definition

在本文中，我们使用小写字母表示标量参数和粗体字母表示向量；此外，粗体矢量符号的上标 i 表示矢量的第 i 个维度。

给定一个无向图 G = (V , E)，其中 V 表示顶点，E 表示边，分别为 E ∈ (V × V )。我们的目标是使用 d |V | 将顶点和各种基序映射到低维空间 Rd 中，通过利用频繁出现的子结构（基序）来捕获顶点的连通性和结构信息。

定义 1.1（主题）。给定一个图 G = (V , E)，基序是子图 G′ = (V ′, E′)，在统计中显着重复，其中 V ′ ⊂ V ； E′ ⊂ E 和 |V ′ | |V|。

2-顶点主题是边缘的别名。 3 顶点和 4 顶点图案广泛用于网络嵌入 [11、22、38、40、50、53] 和 graphlet 计数 [4、6]。因此，在本文中，我们使用 2、3、4 顶点图案，如图 2 所示，并表示为 M0 到 M8。

定义 1.2（主题计数向量）。对于网络中的一个顶点u，我们计算motif count vector cu； cu 的第 i 个维度表示包含顶点 u 的第 i 个类型主题的数量。

2.2 Motif Extraction

Motif提取一直是数据挖掘领域的热门话题。里贝罗等人。 [35] 将基序提取算法分为精确子图计数算法 [4, 19, 32] 和近似子图计数算法 [10, 20]。经典方法枚举所有连接的基序，导致巨大的时间复杂度，而分析算法 [4, 32] 通过数学推导计算基序数。与精确子图计数算法相比，近似子图计数算法在一定程度上权衡了时间复杂度的准确性，可分为随机游走算法[20]和颜色编码算法[10]。从另一个角度来看，motif提取算法可以分为全局motif计数算法和局部motif计数算法[12,19,26,48]。在本文中，我们采用精确子图计数算法 Orca [19]，计算每个顶点的主题计数向量； Orca 的时间复杂度是 O (k ·|E|+T4 )，执行时间的更多细节可以在第 4.7 节中找到。

3 OUR APPROACH

我们提出了一种名为 LEMON 的新表示学习方法，以通用形式连接连通性和结构相似性，并学习顶点和各种图案的理想表示，适用于归纳学习任务。

3.1 LEMON: Learning Representations for Vertices and Motifs

拟议的框架 LEMON 有望做到以下几点：

• （1）桥梁连通性和结构相似性；
• (2) 学习顶点和图案的嵌入；
• (3) 支持归纳学习场景。

我们通过模体提取顶点的结构信息：如果两个顶点的模体计数向量相似，则认为它们在结构上相似。

在我们的模型中，我们将所有主题作为超顶点放入网络中，如算法 1 所示。

顶点和相应主题超顶点之间的结构边被构建；第 i 个主题超顶点 Mi 和顶点 u 之间的结构边的权重，记为 w (u, Mi )，与 ci u 成正比，即包含顶点 u 的第 i 类主题的数量，如下图所示：

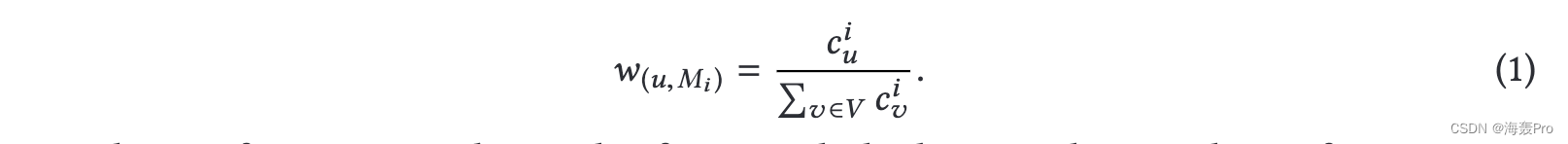
从图 3 可以看出，三角形主题超顶点和顶点 6 ((5, 6, 7), (6, 8, 9)) 之间的结构边的权重大于之间的结构边的权重三角形主题的超顶点和顶点 7 (5, 6, 7)； 2 星主题超顶点和顶点 4 之间的结构边的权重 ((1, 2, 4), (1, 3, 4), (2, 3, 4), (2, 4, 5) , (3, 4, 5), (1, 4, 5)) 大于 2 星主题超顶点和顶点 2 之间的结构边的权重 ((1, 2, 4), (2, 3, 4), (2, 4, 5))。

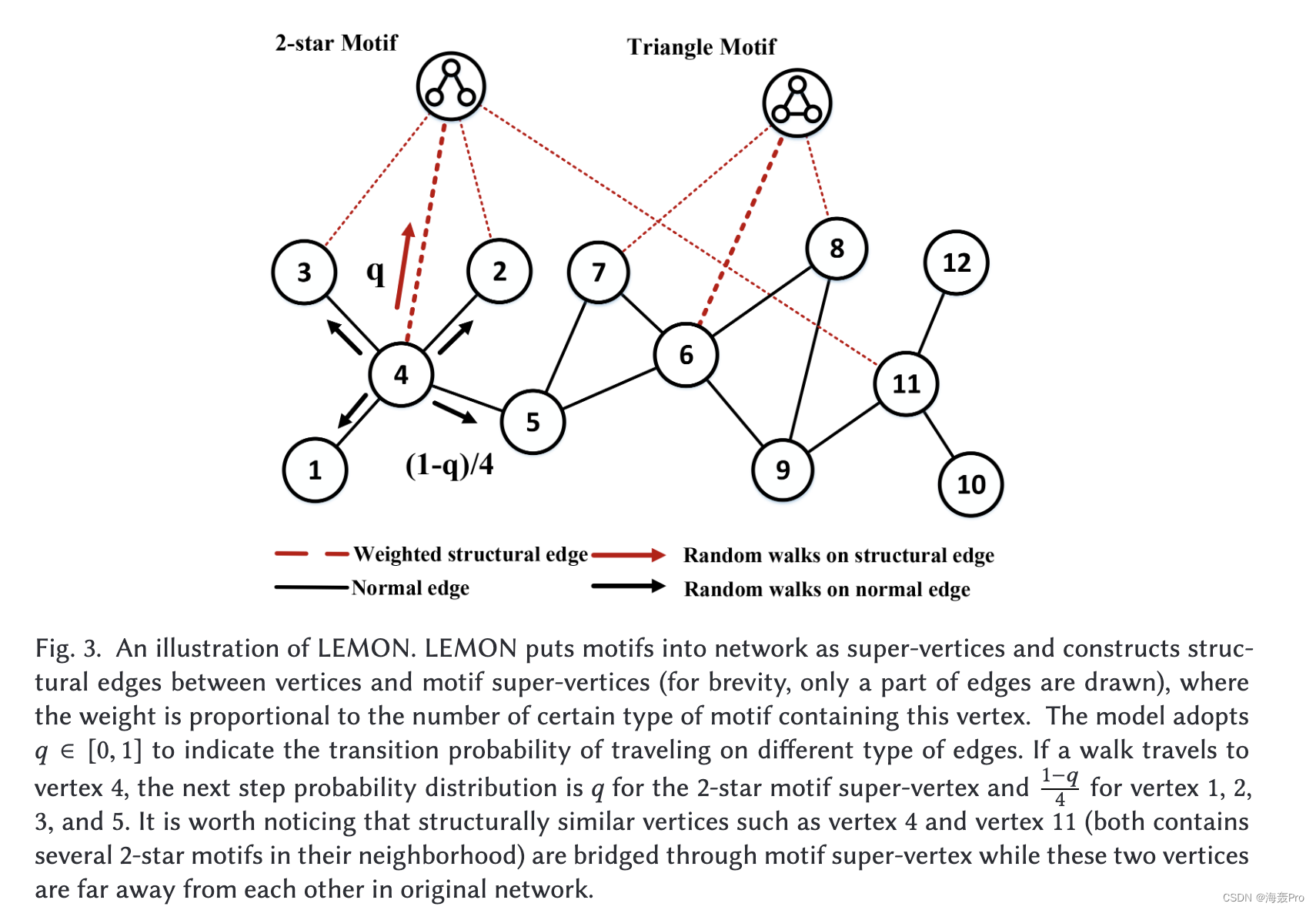
Motif-Step Random Walk：受自然语言处理模型的启发，其中基于语料库训练单词的嵌入向量，DeepWalk [31] 通过将顶点作为单词和执行随机游走以生成路径作为“上下文”。然后它利用 Skip-gram 模型 [27] 来学习有助于预测其上下文的顶点的表示。考虑到我们在网络中有两种类型的边：结构边和正常边，我们提出了一个参数 q 来确定在结构边或正常边上随机行走的概率。1 显然，顶点的嵌入向量应该更相似到那些比其他更频繁地包含该顶点的主题超顶点。作为回应，我们通过提出一种名为motif-step random walk的新策略来改进随机游走策略； πu 表示顶点 u 的主题步随机游走的下一步的转移概率。

如果游走从正常顶点行进，它们在结构边上行进的概率为 q ∈ [0, 1]，在正常边上行进的概率为 1 - q；正常边的权重被视为相同，因此，在正常边上行驶的概率将平均分配给邻居。以图 3 中的顶点 4 为例，如果步行到顶点 4，则顶点 4 的下一步概率分布对于 2 星主题超顶点为 q，对于顶点 1、2、3 为 1−q4，和 5，分别。使用motif-step随机游走策略，顶点及其高度相关的motif超顶点以及被相同类型motif包围的两个顶点将在语料库中彼此靠近，并且它们对应的嵌入向量将被驱动靠近对彼此。

在获得语料库之后，我们将收集到的语料库输入到 Skip-gram 模型 [27] 中，以将顶点映射到低维嵌入向量中。为简单起见，目标函数可以描述为一个优化问题：

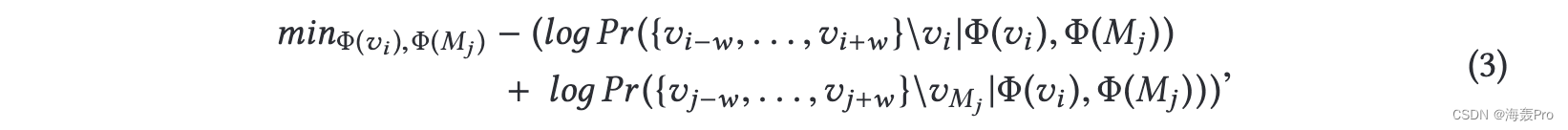
其中 vi , Φ(vi ) 表示顶点 i 和顶点 i 的表示向量，而 Mj , Φ(Mj ) 表示主题超顶点 j 和主题超顶点 j 的表示向量，w 表示窗口大小。对于不同的网络，我们可以根据特定的先验知识调整系数 q。系数 q 越大，随机游走越有可能在结构边缘上传播；该模型更关注结构相似性而不是网络中的连通性。

3.2 Inductive Learning for Unseen Vertices

在动态场景中，顶点以流的形式连续到达网络。如上图所示，LEMON 利用学习到的主题嵌入和顶点嵌入来有效地为看不见的顶点生成嵌入。

LEMON 采用了一种注意力机制，将重要性分配给看不见的顶点周围的不同主题。自然，随机游走越容易获得什么样的主题，这种模式就越重要。特别是，如果随机游走收集的节点经常可以构成某个主题，则说明了这种频繁模式的重要性；每个主题的重要性可以通过这个频率来分配。 2 我们可以重复采用随机游走的过程得到子图，c ̃u = {c0 ̃u , c1 ̃u , . . . , c8 ̃u } 为新到达的顶点 ̃u。具体来说，我们采用从顶点̃u 随机游走来收集一个子图，然后计算它的度向量。将度向量按降序排序后，与图2中列出的不同motif的度向量进行比较。这个过程的时间复杂度可以表示为O(k·nloд·n)，其中k代表重复次数，n表示某个motif中的节点数，在这种情况下，n等于3或4。

看不见的顶点 ̃u 的嵌入向量可以计算如下：

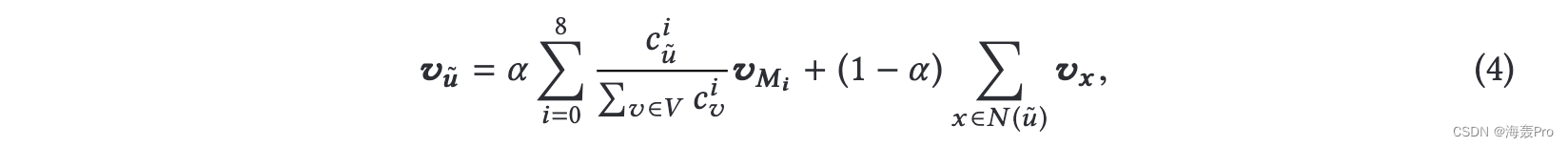
其中 vx , vMi 表示顶点 x 的嵌入向量, ith 类型motif 超顶点,ci u 表示包含顶点̃u 的第i 类型motif 的数量, N (̃u) 表示̃u 的相邻顶点

如图4所示，对于网络中不可见的顶点̃u，我们首先计算其motif count向量，然后通过上式计算顶点̃u的表示向量。具体来说，顶点̃u的表示向量由两部分组成： (a)连通性，由顶点̃u的邻居如顶点v的特征表示； (b) 结构相似性，通过基序的表示来计算。

4 EXPERIMENTS

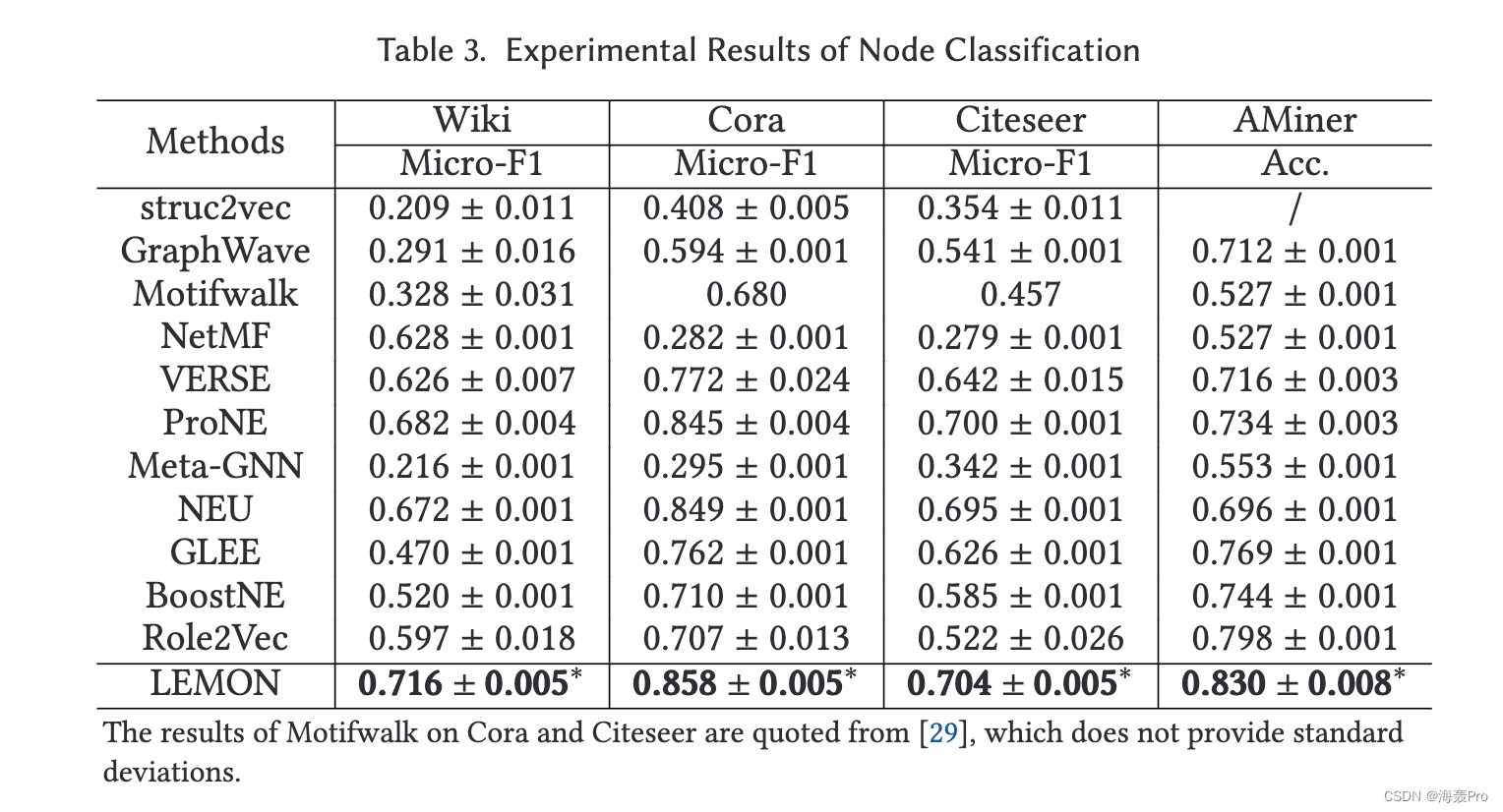
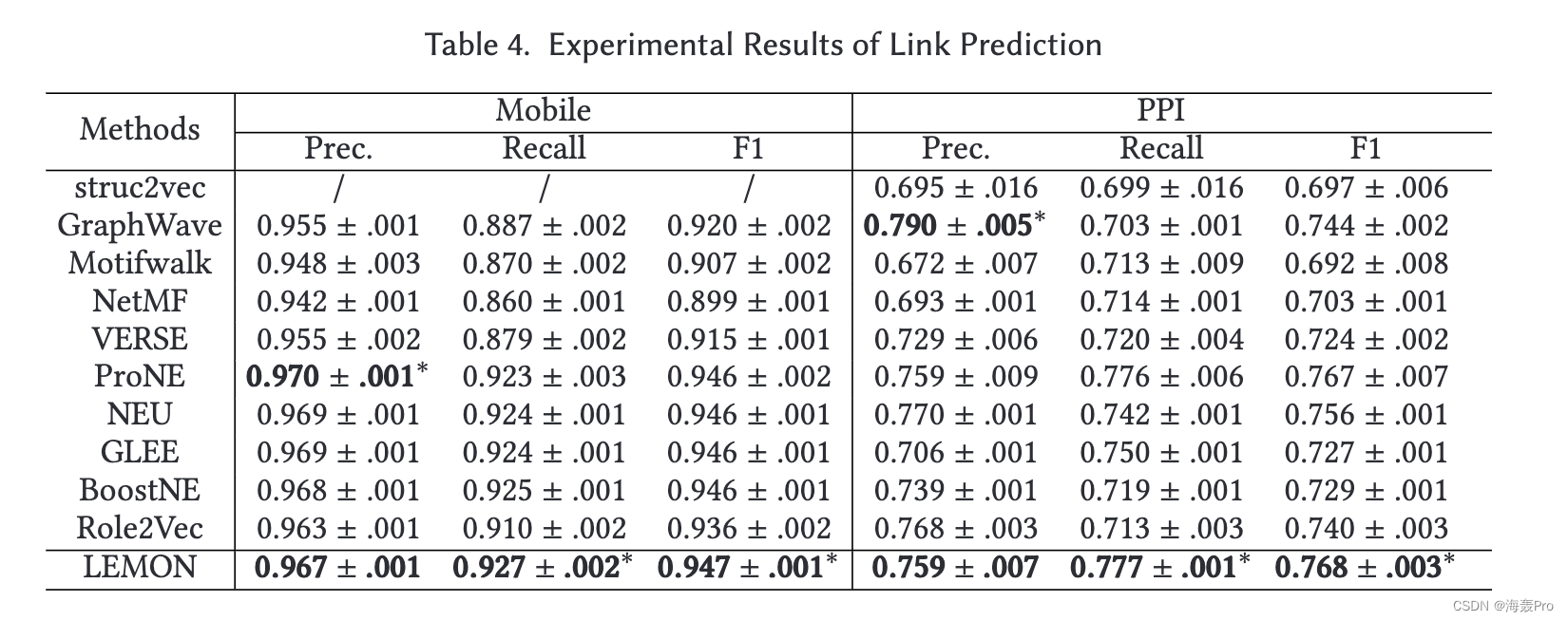
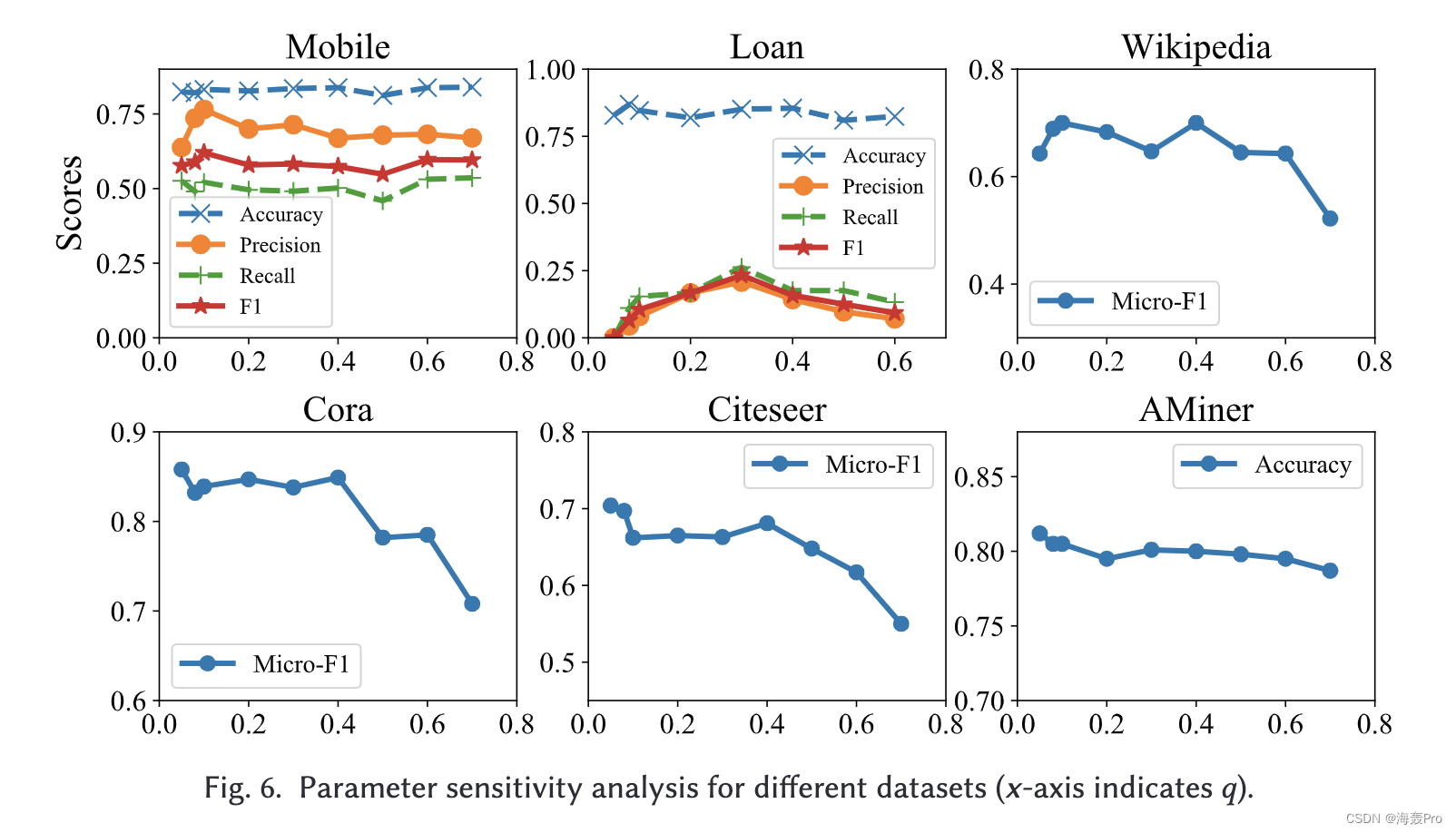
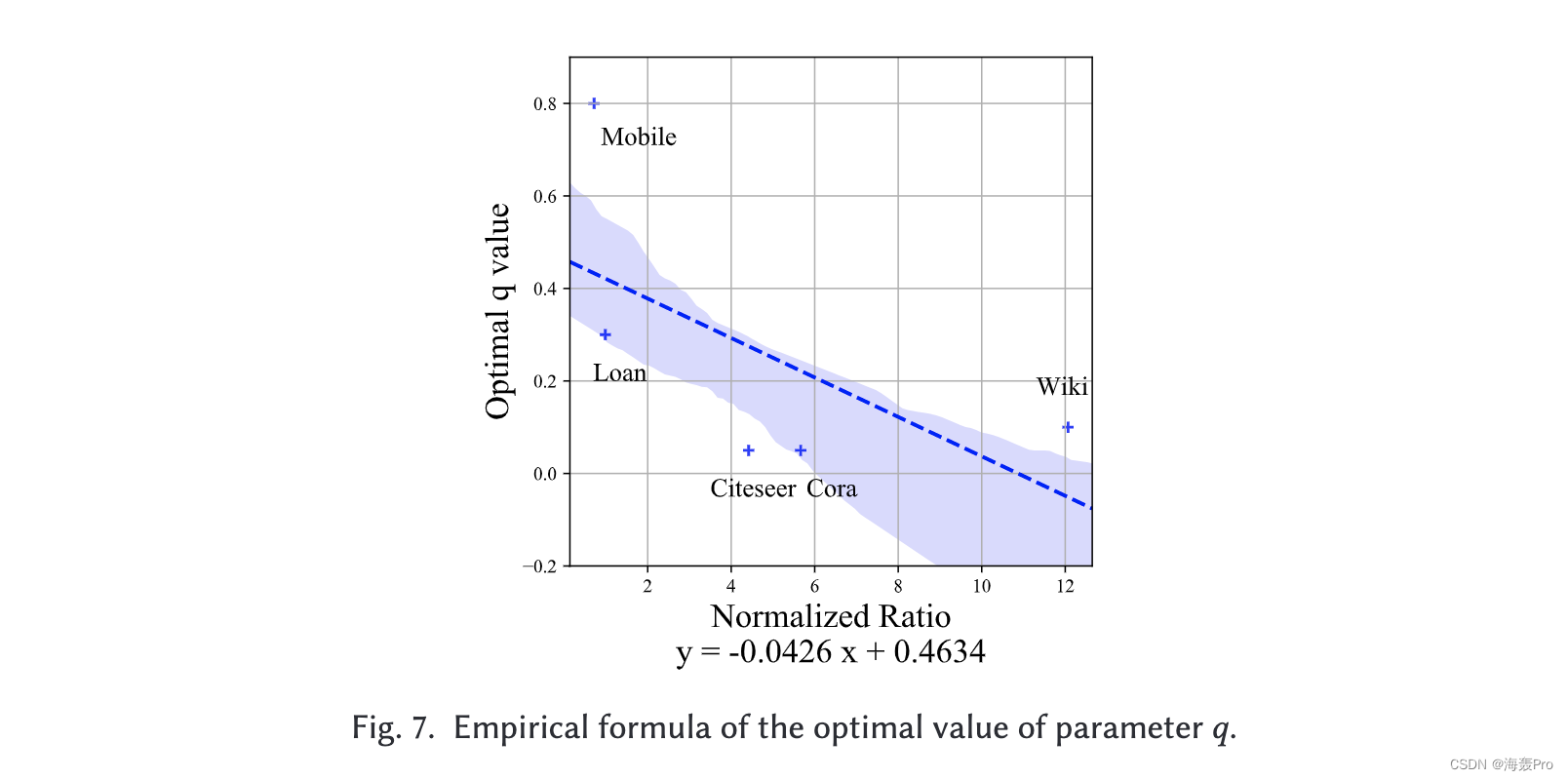
5 RELATED WORK

为了清楚起见，本文的相关工作主要分为两部分：表示学习和主题相关工作。

表征学习。网络嵌入是一个关键领域，在过去的几十年中引起了广泛的研究关注。早期的工作可以追溯到这些基于矩阵分解视角的传统模型[3,30,47]。然而，除了稀疏矩阵分解方法[57]，由于分解大规模矩阵的巨大计算成本，以及其统计性能缺陷[16]，这些模型不可避免地在效率和有效性方面遇到限制。

在网络嵌入研究的文献中，基于随机游走的模型起着重要作用，例如 DeepWalk [31] 保留了顶点与其邻居之间的连接信息。 Node2vec [16] 通过设计一种有偏的随机游走策略来捕获不同的邻域模式，进一步发展了这一想法； LINE [42] 通过一阶和二阶接近度捕获局部和全局结构。此外，GLEE [44] 和 BoostNE [23] 还根据节点的连接属性来学习节点的表示。代表性的基于结构相似性的作品之一：struc2vec [34]，使用顶点的度数作为结构顶点相似性的基础度量。此外，metapath2vec [13] 和 hin2vec [15] 使用元路径随机游走来生成异构网络的上下文。现有的一些作品考虑了多重相似性，例如 VERSE [45]（社区结构、角色和结构对等）； RUM [56]（本地三合会、邻里关系和全球社区接近度）。 RolX [18] 发现顶点的结构角色并使用非负矩阵分解来生成嵌入。同时，Graphwave [14] 将结构相似顶点的谱图小波特征视为概率分布。此外，NEU [51] 通过逼近高阶近似来提高网络嵌入方法的性能。

Motif 相关的网络嵌入。下面概述了一些基于主题学习嵌入的开创性工作： MCN [22] 提出了一种基于主题的注意模型，该模型利用多跳主题邻接矩阵利用高阶邻域。 MotifCNN [40] 采用注意力模型来有效地捕获高阶结构模式信息； [11,37,58]采用基于主题的邻接矩阵，而Nest [50]利用主题过滤和卷积神经网络来捕获结构。 OFFER [55] 通过分别基于节点的主题度和边的主题度来细化邻接矩阵和转移概率矩阵，提高了图表示学习的有效性。有一些作品利用主题来捕获网络中的高阶结构并有效地执行链接预测任务，即 [1, 46]。 HONEM [39] 在学习网络嵌入期间除了成对交互之外还包含非马尔可夫高阶依赖关系。 SNS [24] 将邻居信息和局部子图相似性结合在一起，以提高嵌入的质量。 Sub2Vec [2] 利用随机游走和 word2vec 框架提出了一种基于子图的两个直观属性的可扩展嵌入方法。 Subrank [7] 引入了子图到子图的邻近度度量，并基于个性化的 PageRank 计算子图嵌入。

6 CONCLUSION

在本文中，我们提出了一种新颖的表示学习框架LEMON，它通过motifs以通用形式桥接连接性和结构相似性，并且LEMON能够有效地学习顶点和motifs的表示，这使LEMON能够处理归纳任务。实验结果表明，对于四个不同的任务，LEMON 在两个真实世界数据集和五个公共数据集上优于最先进的算法。

结语

文章仅作为个人学习笔记记录，记录从0到1的一个过程

希望对您有一点点帮助，如有错误欢迎小伙伴指正