机器学习：线性判别分析从理论到公式推导（LDA）

数据定义

DataSet X：= ${(x_i,y_i)}_{i=1}^N,令X的每个观测值xi \in R^p$，Y的每个元素 $y_i\in R$，我们继续化简，X=

Y=

其中 $y_i为+1的输入C1类别，y_i为-1的输入C2$类别。

$$X_c1=(x_i|y_i=+1)$$

$$Xc2=(x_i|y_i=-1)$$

理论概述与变量定义

为了方便可视化，我们先令数据集的维度p=1，也就是每个观测值 $x_i$的维度为1。
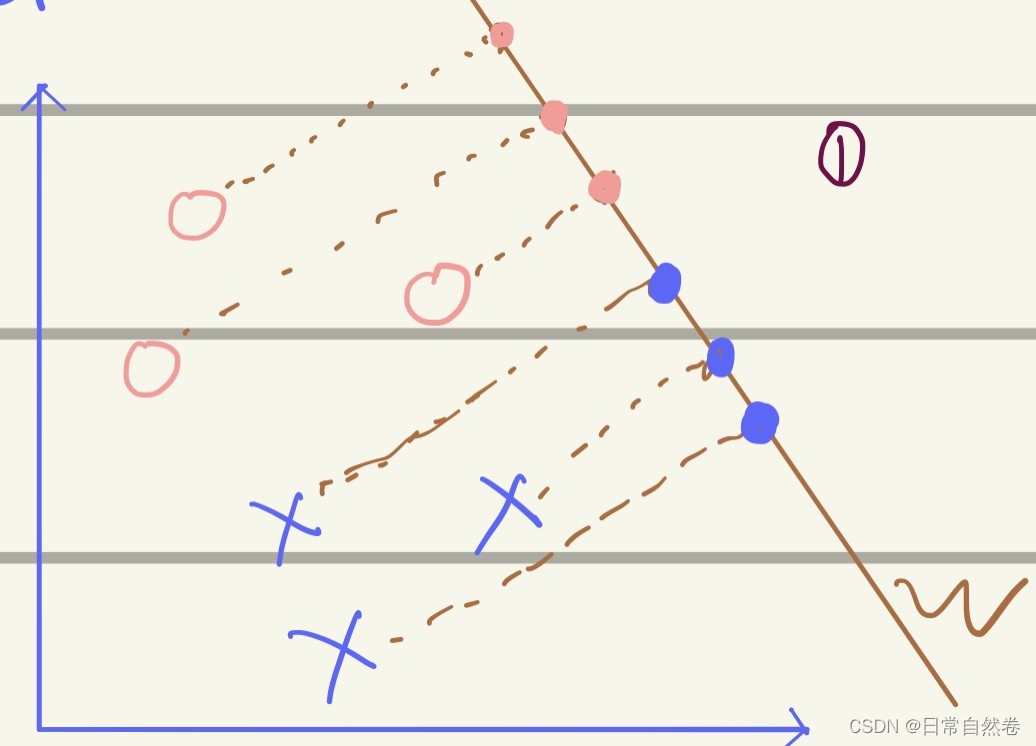
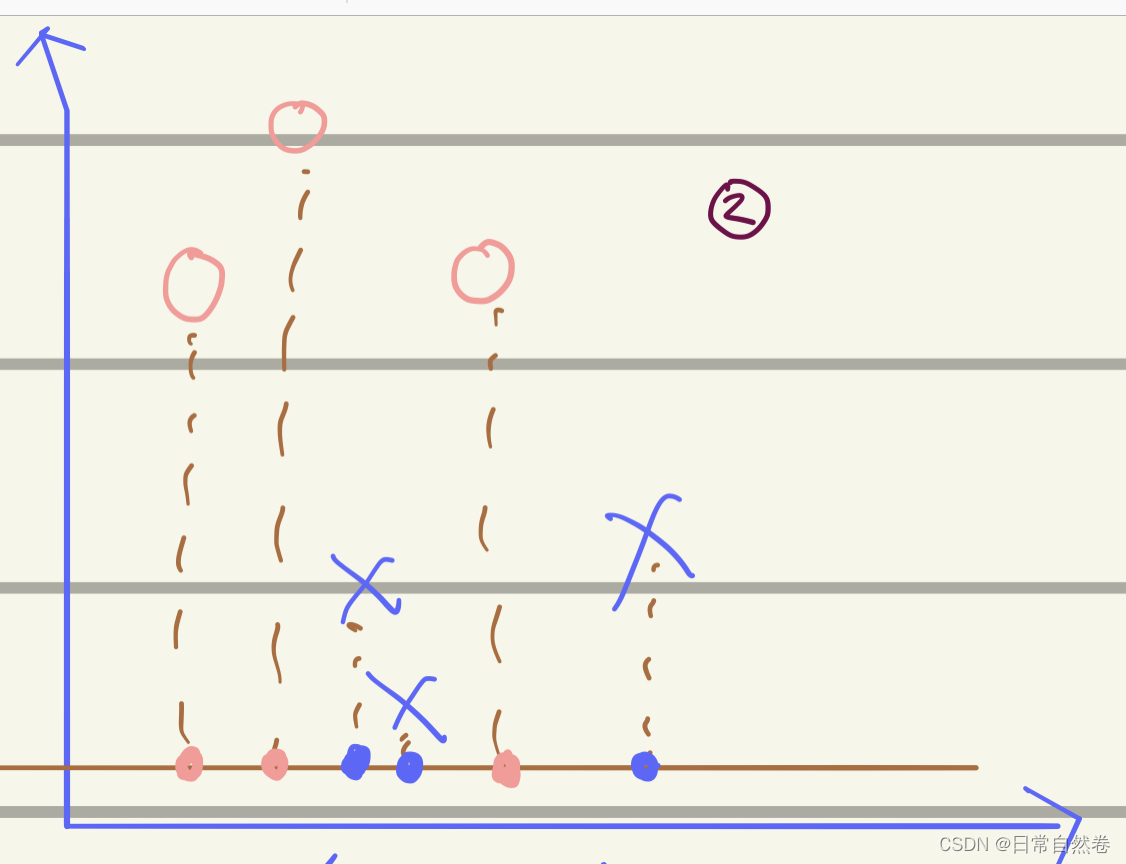
从图中我们可以看到，把这些坐标点投影到一维直线w上，可以发现，当观测值 $x_i$如果投影到了一个合适的Vector上，就会很容易的在Vector上找到一个threshold（阈值），把⭕️与❌分开，但是如果，没有找到一个很好的Vector，就会像下面这幅图：
我们会发现，这两类数据交替出现，不能找一个一个合适的阈值将这两类数据分开。，所以我们要是想把这些数据分开就需要找到一个合适的Vector的方向。
我们通过观察投影到Vector w上面的坐标，我们发现当两类数据的距离越大分类效果越好，每一个分类内之间的数据约紧凑越好。也就是我们要找到一个Vector可以让投影在Vector 上的数据实现：类内小，类间大，还有一种解释：高内聚，松耦合，我起初听到这几句话的时候，感觉特别晦涩难懂，我们通过数学的口吻来解释：
类内小：也就是一个类别的观测值的在Vector上面的投影值之间方差足够小。
类间大：也就是说两个类别的观测值的在Vector上面的投影值的均值差距足够大。
我们现在已经有数据了，那么我们可以通过这个条件来反推出Vector的方向。
下面我们用公式表示：
观测值在Vector上面的投影可以表示为： $z_i=w^Tx_i$,这里我们假设Vector的模 $｜w｜$的值为1（因为我们主要关心的是Vector的方向，长度是可以自由伸缩的）

公式推导

$x_i与w的点乘表示为：|x_i|*|w|*cos\theta,因为|w|=1,所以x_i\cdot w =|x_i|\cdot cos\theta$
均值： $\frac{1}{N} \sum_{i=1}^Nx_i=z_i$
方差： $\frac{1}{N}\sum_{i=1}^{N}(x_i-z_i)(x_i-z_i)^T$
C1：
均值： $\frac{1}{N_1} \sum_{i=1}^{N_1}x_i=z_i$
方差： $\frac{1}{N_1}\sum_{i=1}^{{N_1}}(x_i-z_i)(x_i-z_i)^T=s_1$
C2：
均值： $\frac{1}{N_2} \sum_{i=1}^{N_2}x_i=z_i$
方差： $\frac{1}{N_2}\sum_{i=1}^{{N_2}}(x_i-z_i)(x_i-z_i)^T=s_2$

类间： $(z_1-z_2)^2$
类内： $s_1+s_2$
为了让类内小，类间大，
目标函数 $J(w)=\frac{(z_1-z_2)^2}{s_1+s_2}$
化简分子：
$(z_1-z_2)^2 = (\frac{1}{N_1}\sum_{i=1}^Nw^tx_i-\frac{1}{N_2}\sum_{i=1}^Nw^tx_i)^2$
$=(w^t(\frac{1}{N_1}\sum_{i=1}^Nx_i-\frac{1}{N_2}\sum_{i=1}^Nx_i)))^2$
$=(w^t(\overline{x_1}-\overline{x_2}))^2$
$=w^t(\overline{x_1}-\overline{x_2})(\overline{x_1}-\overline{x_2})^Tw$

$s_1+s_2=\frac{1}{N_1}\sum_{i=1}^N(z_i-\overline{z_{c1}})(z_i-\overline{z_{c1}})^T+\frac{1}{N_2}\sum_{i=1}^N(z_i-\overline{z_{c2}})(z_i-\overline{z_{c2}})^T$
提取w，最终化简结果
$=w^T(s_{c1}+s_{c2})w$
$J(w)=\frac{w^t(\overline{x_1}-\overline{x_2})(\overline{x_1}-\overline{x_2})^Tw}{w^T(s_{c1}+s_{c2})w}$
我们令类间方差差 $s_b=(\overline{x_1}-\overline{x_2})(\overline{x_1}-\overline{x_2})$

令类内方差： $s_w=s_{c1}+s_{c2}$
所以 $J(w)=\frac{w^Ts_ww}{w^Ts_bw}$
我们对目标函数求偏导数，令其等于0.最终得到：
$w=\frac{w^TS_ww}{w^Ts_bw}s_w^{-1}s_bw$
由上面推到中可知： $w的size为1*p s的size为p*$，所以 $w^TS_ww$与 $w^Ts_bw$为一维常数，
由于我们最终需要求的是Vector 的方向，所以我们约去与方向无关的变量。
$w正比于s_w^{-1}(\overline{x_1}-\overline{x_2})$,它的方向也就是最终我们要找的向量的方向。