@TOC

简介

Hello！
非常感谢您阅读海轰的文章，倘若文中有错误的地方，欢迎您指出～
 
ଘ(੭ˊᵕˋ)੭
昵称：海轰
标签：程序猿｜C++选手｜学生
简介：因C语言结识编程，随后转入计算机专业，获得过国家奖学金，有幸在竞赛中拿过一些国奖、省奖…已保研
学习经验：扎实基础 + 多做笔记 + 多敲代码 + 多思考 + 学好英语！
 
唯有努力💪
 
【每日一读】每天浅读一篇论文，了解专业前沿知识，培养阅读习惯（阅读记录 仅供参考）

论文简介

原文链接：https://www.sciencedirect.com/science/article/pii/S0925231222003940?via%3Dihub

期刊：Neurocomputing （CCF-C类）

年度：2022年4月6日（发表日期）

Abstract

知识图（KGs）嵌入近年来得到了广泛的研究。然而，对无处不在的超关系 KG 的了解较少。大多数现有的超关系 KG 嵌入方法将 n 元事实分解为更小的元组，从而破坏了 n 元事实的结构。此外，这些模型总是受到低表达性和高复杂性的困扰。

在这项工作中，为了解决不可分解性问题，我们将 n 元事实表示为超边，保持事实的完整性并保持主要三元组所起的重要作用。

为了解决表达性和复杂性问题，我们提出了 HYPER2，我们将双曲线 Poincaré 嵌入从二进制数据推广到任意数量数据，并且我们设计了一个信息聚合模块来捕获三元组内外实体之间的交互。

大量实验表明 HYPER2 优于其平移和深度类似物，在相对较少的维度上大幅提高了 MRR 和其他指标。此外，我们研究了文字的副作用，并在理论上和实验上将 HYPER2 的计算复杂度与几个性能最佳的基线进行了比较。 HYPER 2 比同类产品快得多。

1. Introduction

大规模知识图谱的出现，如 Freebase [1]、Wikidata [2] 和谷歌的知识图谱 [3] 为从推荐系统 [4]、语义搜索 [5] 到问答 [ 6]和自然语言理解[7]。 KG 通常表示为（头实体、关系、尾实体）形式的一组三元组，其中一个关系链接一个实体对。尽管包含丰富的信息，KGs 仍然面临着不完整的问题。据我们所知，Freebase 中 71% 的人没有出生地属性 [8]。链接预测任务，旨在根据现有链接预测图中实体之间的新链接，解决了这个问题 [9]。已经设计了多种具有代表性的链接预测技术 [10-12] 来处理基于三元组的 KG。而在过去的十年里，我们见证了这一领域的可喜进展。然而，当大量精力投入到二元事实（即三元组）时，我们很少关注涉及两个以上实体的普遍存在的 n 元事实。例如，award_nomination 关系通常涉及一个奖励机构、一个接收者、一个奖项和一个作品。几个表演者也可以同时出现在一场表演中。事实上，在 Freebase 中，超过 1/3 的实体参与 n 元事实 [13]。这些具有更多知识的更高数量的事实更接近自然语言。超关系 KG 中的链接预测为许多下游 NLP 应用程序提供了极好的潜力 [14]。

为了处理更具挑战性的 n 元事实而不将它们分解为三元组，m-TransH [13] 首次提出了基于 TransH 的平移距离模型。 RAE [15] 进一步将多层感知器带入 m-TransH，增量工作带来不断进步。但受限于翻译性质，表现力较弱，还有很大的改进空间。

深度模型最近在 n 元链接预测中越来越受欢迎，就像它们在许多其他任务中盛行一样。 NaLP [16] 优于 m-TransH 和 RAE，但如图 1© 所示，它将一个 n 元事实分解为几个键值对，并且需要为单个事实多次计算相关性。 HINGE [17] 的作者主张主三元组保留 n 元事实的主要结构和语义信息。实验表明，Hinge 大大优于 NaLP，验证了初级三元组的重要性。但如图 1(b) 所示，HINGE 将 n 元事实视为主要二元事实和一组 3 元元组的组合。最近的工作 [18] 证明了一些 n 元事实是不可分解的。以病历关系为例，医生会记录病人吃药后的反应。在临床实践中，患者的反应与他服用的药物密切相关，将反应与药物分开是不合理的。尽管这些深度模型带来了显着的性能改进，但这些深度模型中的 n 元事实被分解为小元组。此外，深度模型总是维持相对较高的计算复杂度。

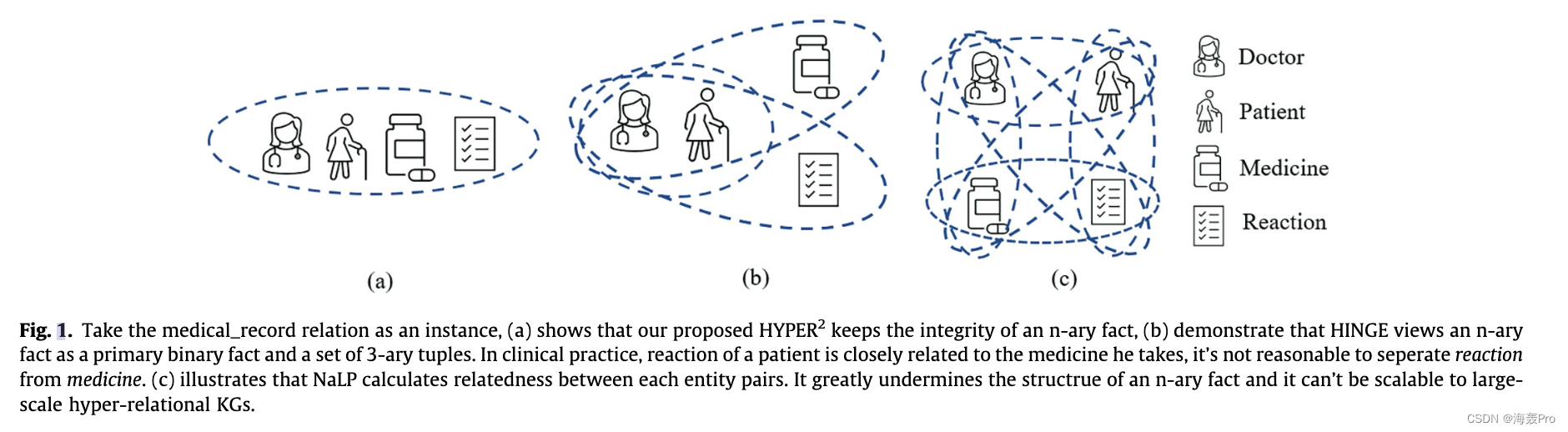
HSimplE [19] 和 HyPE [19] 是卷积模型，但它们只能处理 2 元到 6 元数据。基于张量分解的模型 GETD [20] 也仅适用于单元数据。此外，这三个模型没有明确区分三元组内外的实体，忽略了主三元组的重要性。在这项工作中，我们将一个 n 元事实表示为一个整体超边，如图 1（a）所示，保持事实的完整性并保持主要三元组在 n 元事实中所起的重要作用。

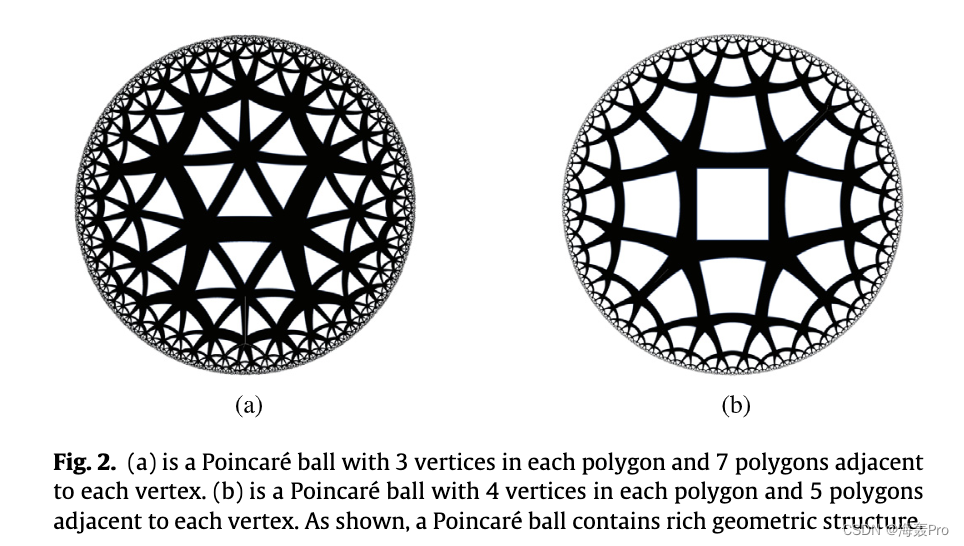
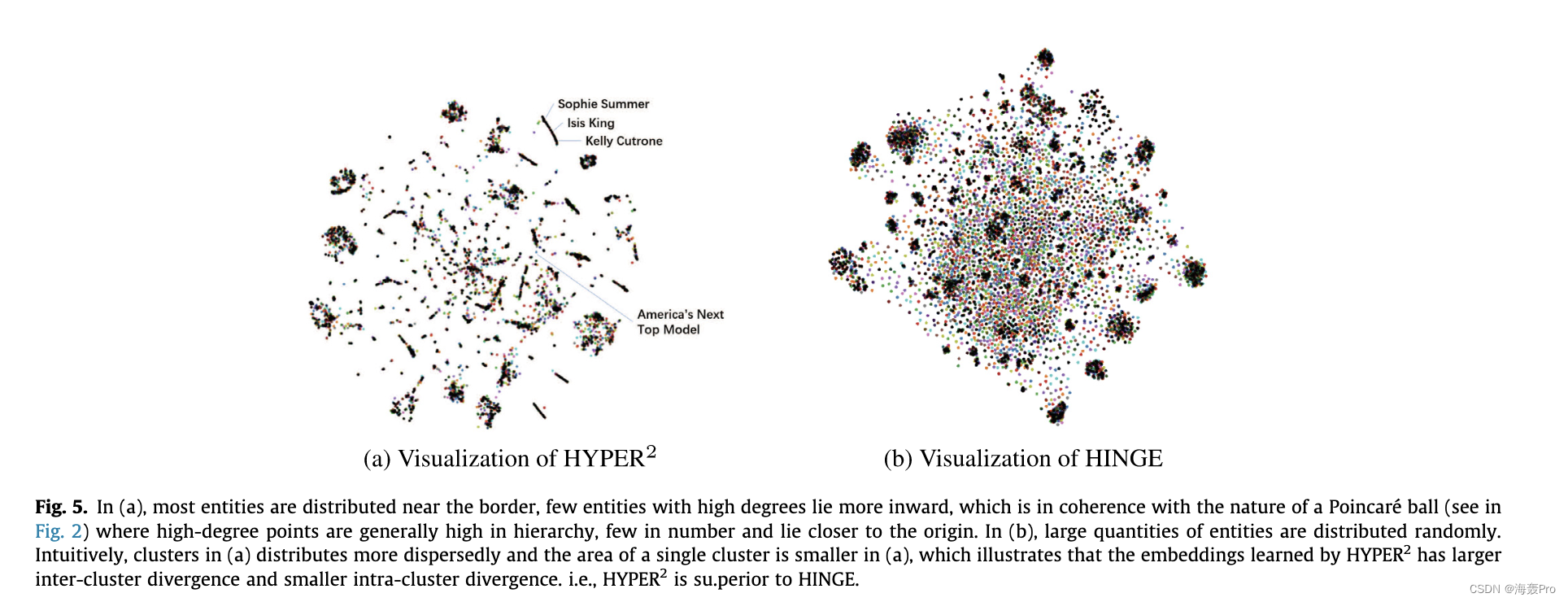
最近，二进制链接预测任务的进展表明**，双曲线庞加莱模型显示出优于其对应物的优越性和较低的复杂性[21]。我们进一步了解到，庞加莱球擅长用层次结构表示知识，以实现双曲空间边界上距离的指数增长。如图2所示，庞加莱球包含丰富的几何结构，在表示复杂的图结构数据方面具有很强的表现力。同样值得注意的是，双曲庞加莱嵌入方法在解决复杂性问题方面具有优势，因为与现有的深度模型相比，它涉及的矩阵加法和乘法运算要少得多**。据我们所知，它尚未在超关系 KG 中进行过研究。

考虑到表现力和低复杂度，我们认为双曲庞加莱嵌入方法对于高效和有效的模型都是有希望的。在这项工作中，我们提出了一个广义的双曲庞加莱嵌入框架，该框架适用于任意数量的事实，称为 HYPER 2。在 HYPER2 中，所有实体首先在双曲空间上随机初始化，然后通过双曲空间和切线空间之间的向量投影以及切线空间上的信息聚合，HYPER2 捕获主三元组和附属实体之间的交互。

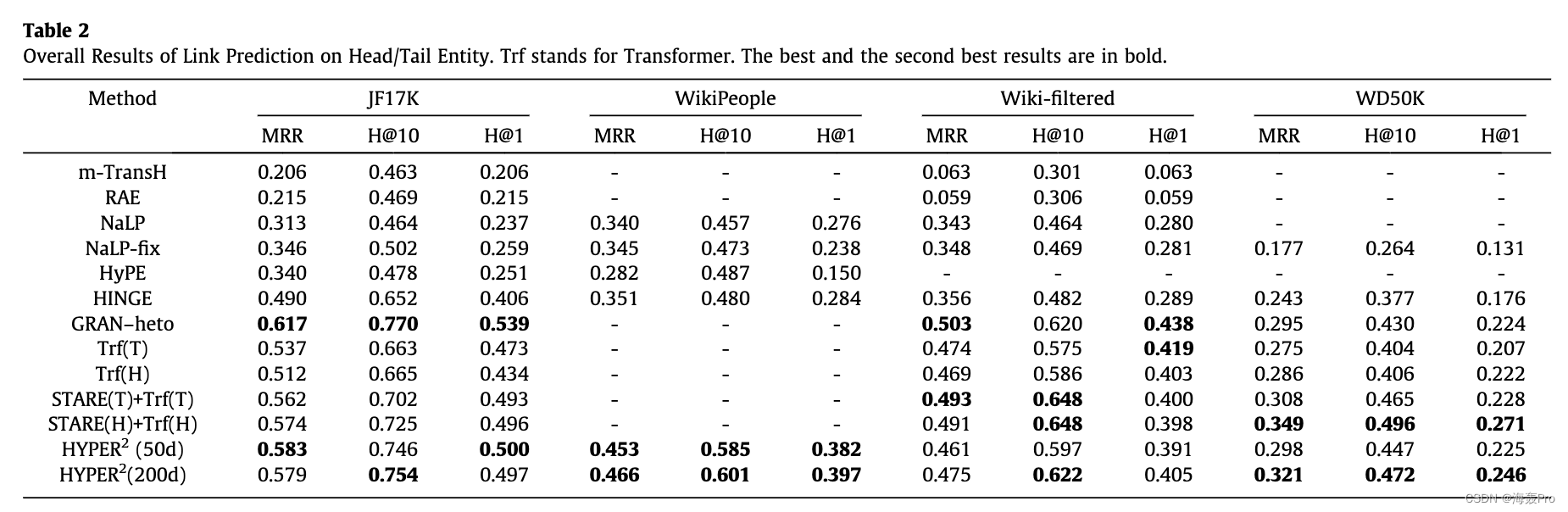
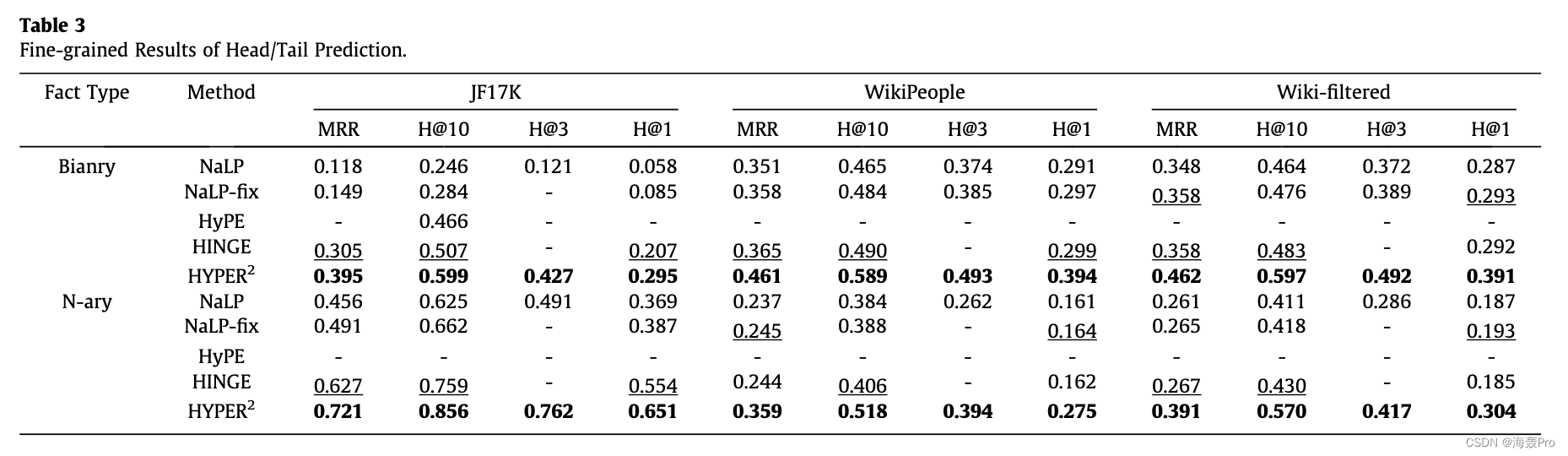
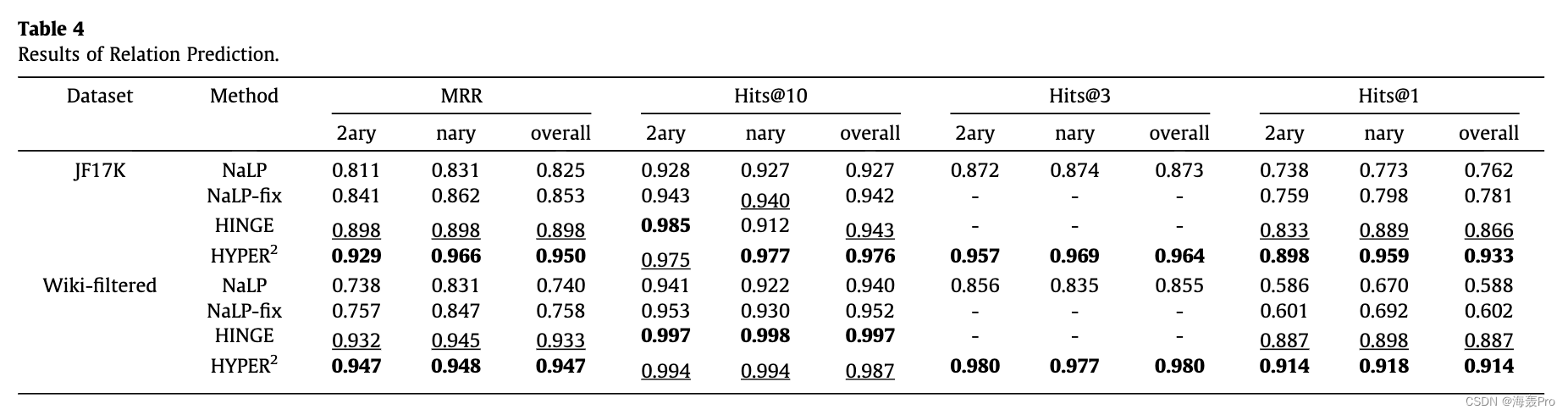
HYPER2在两个具有代表性的超关系数据集上取得了优异的成绩，在WikiPeople上的HITS@1、HITS@10、MRR分别提高了34.5%、21.9%、29.1%，在JF17K上分别提高了23.1%、14.4%、18.9%，验证了有效性和优越性我们的模型。此外，HYPER2 的计算复杂度较低，与其类似物相比要快 49-61 倍。此外，我们的实验验证了文字（数值、日期时间实例或其他字符串）阻碍了嵌入学习。我们的贡献可以总结如下：

• HYPER2 采用超关系来规避将 nary fact 分解为更小的元组，同时考虑到主要三元组在 n-ary fact 中的重要作用以及一些 n-ary fact 的不可分解性。
• 据我们所知，我们提出的 HYPER 2 是第一个使用双曲线 Poincaré 球进行超关系 KG 的模型，HYPER2 将双曲线 Poincaré 方法从二元到任意数量事实推广，说明了高度的灵活性
• 对两个具有代表性的超关系 KG 进行的大量实验表明，我们在 HYPER2 中的信息聚合模块可以有效地捕获初级三元组内外的交互。 HYPER2实现了优于同类产品的性能，性能提升幅度惊人，显示出绝对优势。
• 我们验证了 Wikipeople 数据集中文字带来的副作用。我们在理论上和实验上将 HYPER 2 的参数大小和计算复杂度与之前几个表现最佳的基线进行了比较。实验表明，我们的模型大大压倒了它的同行，表现出低复杂性。

2. Related Work

2.1. Graph Embedding Approaches in non-Euclidean Geometry

在非欧几里得空间中嵌入图形数据的工作越来越多。 Nickel 和 Kiela 在 [22] 的 Poincaré 球上的词汇数据库 WordNet 中将双曲线嵌入引入到链接预测中，他们表明低维双曲线嵌入在泛化能力方面能够显着优于其高维欧几里得对应物和代表能力。随后，同一团队将分层数据嵌入到双曲几何的洛伦兹模型中 [23]。将双曲几何与深度学习相结合，提出了双曲神经网络 [24]、双曲注意力网络 [25] 和双曲图卷积网络 [26]。最近，人们注意到在数据中可以找到像圆形结构这样的非均匀层次结构 [27]，因此图形开始嵌入到具有不同曲率（球形、双曲线和欧几里得）分量的乘积流形上。继 Poincaré GloVe [28] 之后，另一种基于多关系 Poincaré 的方法 Murp [21]，采用双线性评分函数和对头尾实体的偏差，在建模层次结构中显示出强大的表达能力。在[29]中，双曲庞加莱嵌入与RotatE [30]相结合。据我们所知，在双曲线庞加莱球上嵌入超关系 KG 尚待探索。

2.2. Binary Link Prediction

按评分函数分组，二元关系知识图谱中的链接预测模型大致可以分为三类：平移距离模型、神经网络模型和语义匹配模型。

平移距离模型在关系执行平移操作后计算实体距离。 TransE [11] 是最早的平移距离模型，但它无法表示 1N,N-1,N-N 关系。自 TransE 以来，已经提出了各种变体，例如 TransH [31]、TransR [32]、TransMS [33] 来克服这个问题。

随着深度学习的繁荣，各种深度模型应运而生。 ConvKB [34]、ConvE [12] 利用卷积网络。 RSN [35]通过残差学习来学习利用知识图中的长期关系依赖。 R-GCN [36] 和 GAE [37] 将图卷积网络应用于 KG 模型。借助各种神经网络结构，这些模型取得了优异的结果[38]。

RESCAL [10]、DistMult [39]、ComplEx [40] 和 TuckER [41] 等语义匹配模型是双线性框架。 RotatE [30] 将关系视为从头部实体到尾部实体的旋转。 QuatE [42] 将嵌入从复杂空间扩展到超复杂空间。 HAKE [43] 将实体映射到极坐标系以对语义层次结构建模。 Murp [21] 将实体映射到双曲空间中的庞加莱球以捕获语义层次结构。与基于神经网络的模型相比，双线性模型取得了具有竞争力的结果，但更易于解释。

2.3. Hyper-Relational Link Prediction

在更具挑战性的超关系知识图谱中预测新链接的方法大致可以分为平移距离和基于神经网络的模型。

在平移距离模型方面，m-TransH [13] 是第一个处理超关系 KG 的工作。 m-TransH 直接将 TransH 从二元事实扩展到 n 元事实，作为 n 元链接预测的开创性工作，在 JF17K 数据集上的实验表明 m-TranH 超过了 TransH 一个令人愉快的幅度。 RAE [15] 进一步将多层感知器引入 m-TransH。这两个模型的翻译性质使它们无法充分表达更复杂的 n 元关系 [44]。

NaLP、HSimplE [19]、HypE [19]、NaLP-fix [17]、HINGE 等都是深度模型。 NaLP 在 JF17K 和 WiKipeople 上的表现都优于 m-TransH 和 RAE。然而，在 NaLP 中，一个 n 元事实被撕成 n 个键值对。类似于三元分解，这种成对分解也可能极大地破坏 n 元事实的结构。 HINGE 将 n 元事实视为主要的三元组和 2 个五元组，使用卷积神经网络捕获三元组特征和五元组特征。 Hinge 的作者还提出了 NaLP 的一种变体，即 NaLP-fix，其中模型结构保持不变，但给出了新的负采样策略。 HSimplE 和 HypE 为具有不同数量的事实设计了一组卷积核，具有灵活性。 GETD [20] 将 Tucker 扩展到 n 元情况，即 n-Tucker，并将张量环分解进一步集成到 n-Tucker 中。 GETD 不灵活，仅适用于 3 进制和 4 进制数据。此外，三元组内外的实体没有明确区分。 STARE [45] 采用图神经网络编码器和变压器解码器，STARE 的作者提出了 WD50K 数据集。但是该模型非常耗时。 GRAN [46] 目前是最先进的模型，它利用异构网络对 n 元事实进行建模。

我们的 HYPER 2 考虑了主要三元组的重要作用和 n 元事实的完整性。此外，利用庞加莱球的优势，HYPER2 需要的参数更少。

3. Preliminary

3.1. Basic Concepts

超关系知识图包含二元事实和 n 元事实，我们将主要三元组内外的实体分别作为主要实体和附属实体。超关系知识图谱中的链接预测任务包括头/尾实体预测、关系预测和附属实体预测。我们将在下面给出它们的定义。

定义 1（超关系知识图谱）。给定一个具有一组关系 R 和一组实体 E 的超关系 KG G，超关系 KG 中的一个事实包含一个关系和任意数量的实体。形式上，一个事实可以写成一个 tupleF ：ðr; e1; e2; . . . EI； . . . ; enÞ, 其中 r 2 R; ei 2 E.n代表参与元组F的实体数量。如果n 1/4 2； F是二元事实。如果 n > 2; F 是一个 n 元事实，r 是一个超关系，它不同于超图中包含标签和方向信息的边。我们取ðr; e1; e2Þ 作为主要三元组。初级三元组内的实体，即 e1； e2 ，被视为主要实体，超越主要三元组的实体，即 {eiji 2 ð2; n; i 2 Z} 表示为附属实体。

以詹姆斯·霍纳凭借在《勇敢的心》中的出色表现获得第 68 届奥斯卡金像奖最佳原创戏剧配乐提名这句话为例。句子中隐含的事实可以写成(be_nomination_for, James Horner, the 68th Academy Awards for Best Original Dramatic Score, BraveHeart) 其中James Horner 是头部实体，第68 届奥斯卡最佳原创剧情得分是尾部实体，这两个实体都是主要实体。而BraveHeart是附属实体，被提名为超关系。

定义 2（超关系链接预测任务）。假设 G 是一个不完整的超关系知识图谱，超关系链接预测任务旨在根据 G 中的已知事实推断缺失的事实。在实践中，问题被简化为预测部分事实的缺失实体或关系。在这项工作中，预测部分事实ðr的主要实体； ?; e2; . . . ; e 我; . . . ; enÞ 或 ðr; e1; ?; . . . ; EI； . . . ; enÞ表示为头/尾实体预测，推断ðr的缺失实体； e1; e2; . . . ; ?; . . . ; enÞ 被称为附属实体预测。同时预测缺失关系ð?; e1; e2; . . . ; EI； . . . ; enÞ 被命名为关系预测。

3.2. Hyperbolic geometry of the Poincaré ball

d 维庞加莱球 ðPd K ;半径为 1ffiffiffiKp ðK > 0Þ 的 gPÞ 是一个真实的光滑流形 Pd K 1/4 x 2 Rd : K xk k2 < 1n o; gP 是符合欧几里得度量 gE 的黎曼度量，即 gE 1/4 Id。我们有 gP 1/4 kKx 2gE，其中 kKx 1/4 2=ð1 xk k2Þ 是保形系数。对于每个点 x 2 Pd K ，度量张量 gP 定义了一个正定内积 TxPd K TxPd K ！ R; TxPd K 是在 x 处与 Pd K 相切的 d 维欧几里得空间。要将点 x 2 Pd K 投影到其对应的切线空间 TxPd K 上，存在一个对数映射 logKx ： Pd K ！ TxPd K。逆是指数映射 expKx : TxPd K ！钯钾。对于庞加莱球，它们是：

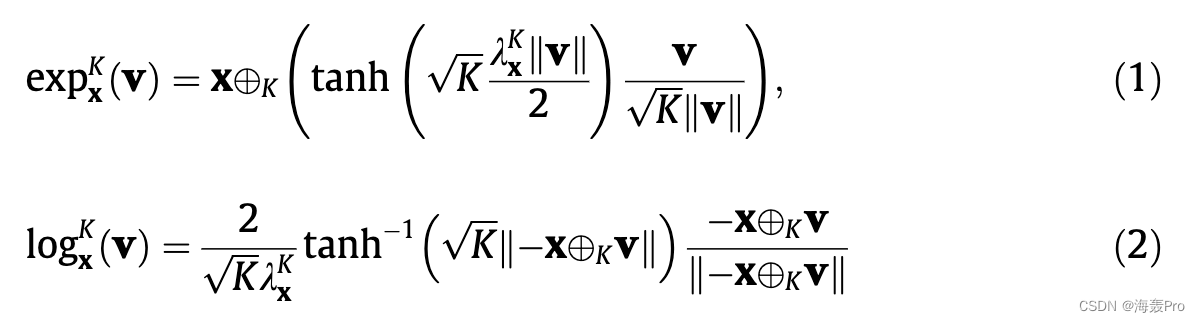
其中 v 2 TxPd K 是在 x 处与 Pd K 相切的向量； k k 表示欧几里得范数，K 表示莫比乌斯加法 [47]：

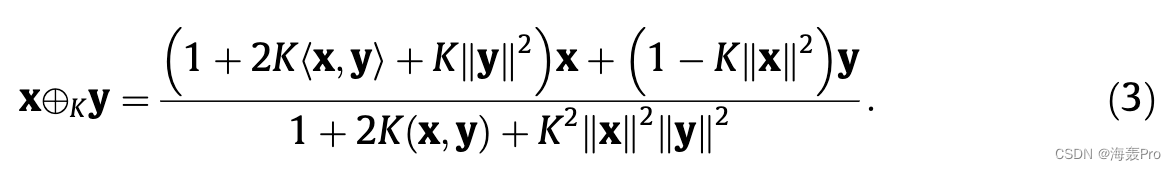
h 代表欧几里得内积。看公式，指数（对数）映射主要涉及非线性双曲正切（inverse hyperbolic tangent）运算、除法、范数和莫比乌斯加法。与卷积层和全连接网络所涉及的大量计算相比，这些看似复杂的公式实际上需要更少的时间来计算。我们将在第 5 节中从理论上和实验上分析几个深度模型的计算复杂度。矩阵向量乘法也有一个莫比乌斯对应物 [24]：

在 (4) 中，点 x 2 Pd K 首先用对数映射投影到欧几里得切空间 0 2 Pd K 处，然后乘以矩阵 M 2 Rd d，最后投影回双曲空间 Pd K指数地图。我们模型中的矩阵 M 是对角的，进一步降低了计算复杂度。两点之间的距离x； y 2 Pd K 由测地线长度给出。

测地线定义了位于给定表面中的两点之间的最短路径。在欧几里得空间中，测地线是连接两个端点的线段，而对于庞加莱球，测地线如图 3 所示，测地线的长度由下式给出：

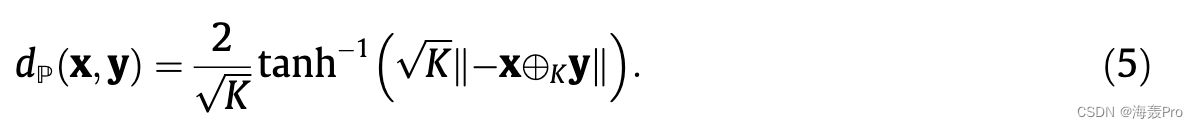
计算测地线的长度也不繁琐。随着庞加莱球的双曲几何的引入，我们还证明了庞加莱球在计算复杂性方面优于其对应物。在接下来的部分中，我们将介绍有关我们方法的更多细节。

4. Hyperbolic Poincaré Embedding for Hyper-Relational Link Prediction

大多数图结构数据都具有固有的几何结构，超关系知识图谱也不例外。在这些几何结构中，树状的层次结构是通用的。双曲庞加莱嵌入方法，据我们所知，它擅长于表示层次结构，并且尚未在超关系 KG 中进行研究，有望成为一种有效且高效的多元链接预测模型。我们建议 HYPER2 在双曲线庞加莱球上的超关系 KG 中嵌入任意 ariry 事实。

4.1. Affiliated Information Specific Entity Representation

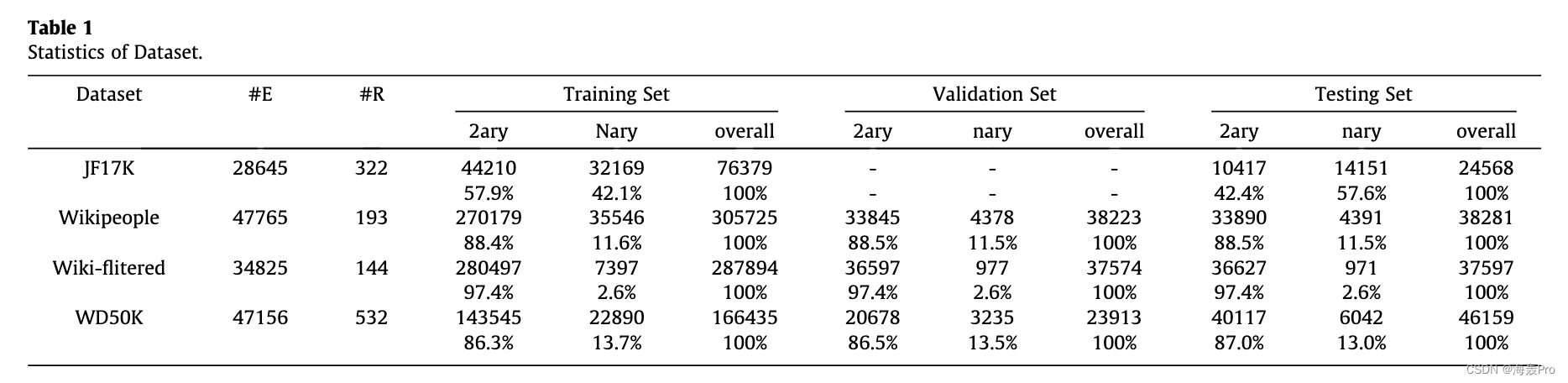
Fact 在 JF17K 中是 ðr 的形式； e1; e2; . . . ; enÞ，而 WikiPeople 和 WD50K 中的 fact 组织为 ðeh； r;等； r1;一个； . . . r 我;我; . . .Þ.由于 HYPER2 将 n 元事实中的关系视为超关系，因此我们只保留超关系 r。三个数据集中的事实都表示为ðr；嗯；等；一个； . . . ;艾; . . . a2Þ。 HYPER2的结构如图4所示。

主三元组在 n 元事实中起着至关重要的作用，并保留了事实的主要信息。考虑到初级三元组的重要性，嗯； et 被视为主要实体，ai；我 2 ð2; n 2 被视为关联实体。尽管主要三元组的重要性，附属实体中的丰富信息是不可忽略的。附属实体可以使主要三元组更具体。捕获主要三元组和附属实体之间的交互是很重要的。考虑到这一点，我们设计了一个信息聚合器来绘制附属信息特定实体表示。

详细地说，在我们的模型中，超关系和 n 元事实 F 中的所有实体：ðr;嗯；等；一个； ; a n 2Þ 首先被初始化为 d 维向量 r；嗯；等；一个； , 一个庞加莱球 Pd K 上的 2 ，然后所有实体都投影到具有对数映射的切线欧几里得空间。为了对主要三元组和附属实体之间的动态交互引入的有用信息进行建模，我们将每个附属实体 ai 的潜在向量按元素分别添加到头实体和尾实体：

随后，我们将嵌入与相关信息连接起来，并执行逐元素最小化操作：

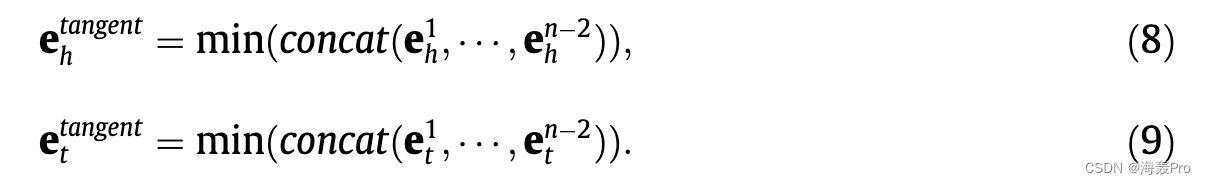
我们利用最小化操作，假设用较少关联信息判断是非的框架是一个更好的模型。我们的目标是 1）判断一个有效的 n 元事实是真实的，只有很少的附属信息存在。 2）在没有大量附属信息的情况下，将无效事实判断为虚假。以类似的方式，之前的工作 NaLP 和 HINGE 已经成功地合并了源自神经网络的关联向量。最后，关联信息特定实体表示，即切线 h；正切 t ，用指数映射投影回双曲空间：

当 n = 2 时，即没有附属实体参与事实，我们的模型可以推广到二进制 Poincaré 嵌入模型 Murp。在 HYPER2 中，所有实体都在双曲空间上初始化，然后投影到切线空间，在此我们通过元素最小化和加法运算符捕获交互并聚合主要实体和附属实体的信息。然后将那些具有聚合信息的实体投影回双曲空间。接下来，我们将给出评估一个事实的评分函数。

4.2. Scoring Function

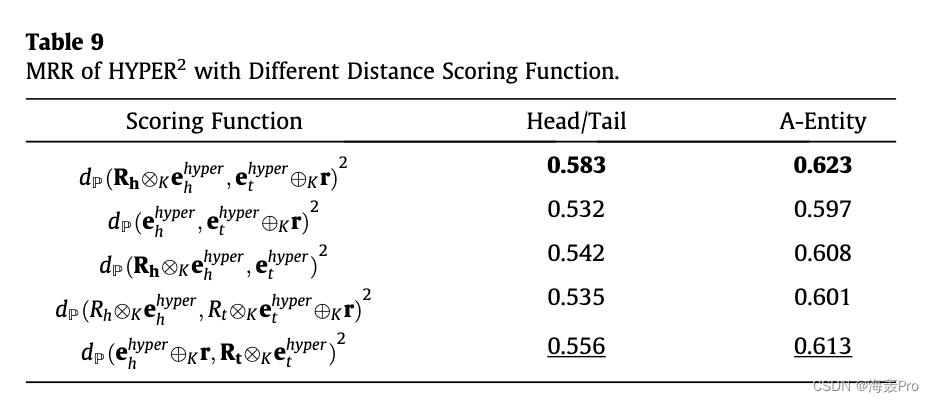
双线性模型的评分函数包含头部实体嵌入、关系矩阵和对象实体嵌入之间的双线性乘积。双线性模型的有效性已在 [10]41 中得到验证。然而，在双曲空间中不存在欧几里得内积的明确替代。在 Poincaré Glove [28] 的基础上，我们用距离函数对内积进行建模，即 hx； yi 1/4 1 2 ð dðx; yÞ2 þ xk k2 þ yk k2Þ，我们用 bh 和 bt 代替平方范数。此外，受到 [21] 的启发，它分别对头部实体和尾部实体应用关系特定的转换，即通过对角谓词矩阵 R h 2 Rd d 到头部实体的拉伸和通过 d 维向量偏移 r 到尾部的平移实体，对事实 F 进行评分的基本评分函数可以如下给出：

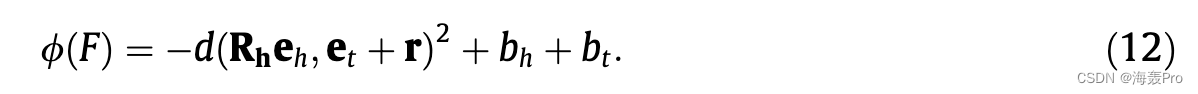
在我们的 HYPER2 中，关联实体的信息已经聚合到主要实体中，因此评分函数既可以反映主要三元组的合理性，也可以反映整个事实的合理性。取 (12) 的双曲线类比，我们可以将 HYPER2 的评分函数定义为：

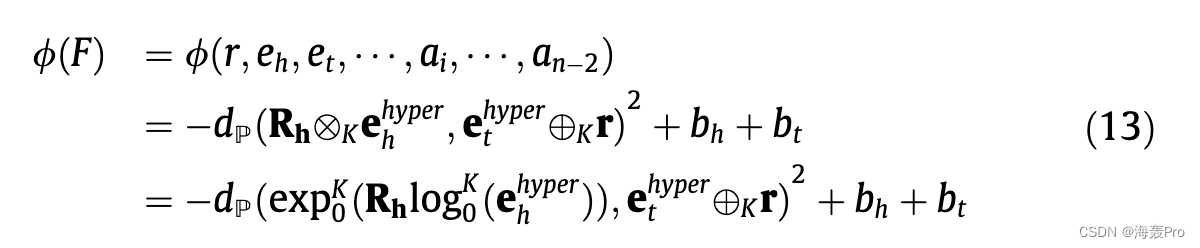
我们用它们的莫比乌斯等价物替换欧几里得加法和矩阵向量乘法。我们用它们的附属信息特定形式替换了头部和尾部实体表示。 HYPER2 适用于任意数量的事实，具有高复杂性。在没有附属实体的情况下，HYPER2 可以推广到 Murp [21]，保留对三元组建模的能力。

4.3. Training and Optimization

作为一种常用的数据增强方法[21,48]，我们还引入了倒数关系ðr 1；等；嗯；一个； ;每个事实 F 的 2Þ : ðr; e h;等；一个； ;数据集中的 n 2Þ。我们通过随机破坏实体域或关系域为训练集中的每个真实事实生成 nneg 个负样本。具体来说，我们破坏了与关系集 R 中另一个随机选择的关系的关系。而对于实体，我们破坏了头部实体ðr； e0h;等；一个； ;一个 2Þ，尾部实体 ðr；嗯； e0t ;一个； ;一个 n 2Þ 或附属实体 ðr 之一；嗯；等； ; a0i; ;一个 n 2Þ 从整个实体集 E 中随机选择一个实体。训练模型以最小化二元交叉熵损失：

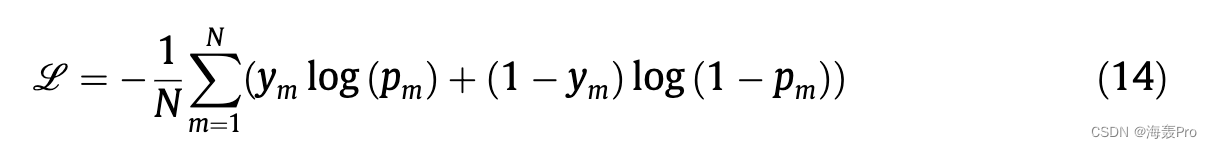
其中 N 代表训练样本的数量，ym 是指示事实是否为正的二进制标签，pm 1/4 rð/ðFÞÞ 表示预测概率，rð Þ 是 sigmoid 函数。我们使用黎曼随机梯度下降 (RSGD) [49] 优化模型。 RSGD 和 SGD 之间存在两个主要区别。一个是梯度的计算，黎曼梯度rRL是欧几里得梯度rEL乘以庞加莱度量张量的倒数即rRL 1/4 1kKxð Þ2 rEL，另一个区别在于更新步骤，欧几里得更新步骤为：

而黎曼更新步骤是：

HYPER2 的训练过程在算法 1 中给出。

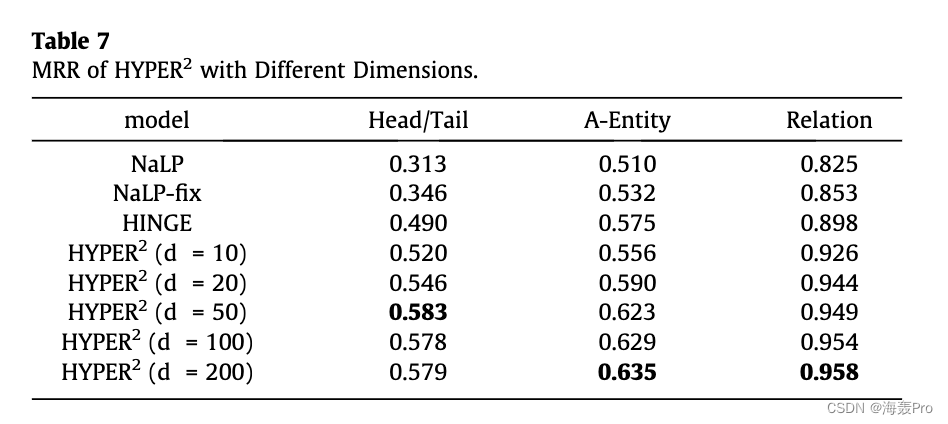
5. Experiments

6. Conclusion

知识图谱通常以三元组结构存储。因此，现有的知识图嵌入框架通常通过三元组学习实体和关系嵌入。现有模型试图避免将 n 元事实分解为三元组，但仍引入五元组分解。在这项工作中，我们完全避免了 n 元事实的分解，保持了事实的完整性并保持了主三元组。我们提出了 HYPER2，这是一种用于超关系链接预测的有效且高效的双曲庞加莱嵌入方法，它首先将实体和关系映射到双曲庞加莱球上，然后在切线空间上聚合来自主要三元组和附属实体的信息。在两个基准数据集（JF17K、WikiPeople 和 WD50K）上进行的大量实验证明了 HYPER2 相对于其类似物的优越性，大大优于其平移和深度框架。此外，我们进一步从理论上和实验上证明了 HYPER2 在参数大小和计算复杂度方面具有优势。此外，我们发现 WikiPeople 中的文字可能会阻碍学习合适的嵌入。至于未来的工作，我们计划通过考虑实体类型和多模态数据，对超关系 KG 嵌入进行更深入的研究。

结语

文章仅作为个人学习笔记记录，记录从0到1的一个过程

希望对您有一点点帮助，如有错误欢迎小伙伴指正