@TOC

简介

Hello！
非常感谢您阅读海轰的文章，倘若文中有错误的地方，欢迎您指出～
 
ଘ(੭ˊᵕˋ)੭
昵称：海轰
标签：程序猿｜C++选手｜学生
简介：因C语言结识编程，随后转入计算机专业，获得过国家奖学金，有幸在竞赛中拿过一些国奖、省奖…已保研
学习经验：扎实基础 + 多做笔记 + 多敲代码 + 多思考 + 学好英语！
 
唯有努力💪
 
【每日一读】每天浅读一篇论文，了解专业前沿知识，培养阅读习惯（阅读记录 仅供参考）

论文简介

原文链接：https://ieeexplore.ieee.org/document/9305271

期刊：IEEE TRANSACTIONS ON NETWORK SCIENCE AND ENGINEERING

年度： 2020 年 12 月 23 日（发表日期）

Abstract

网络嵌入是学习顶点低维表示的任务，最近引起了越来越多的关注。有证据表明，许多现实复杂网络的隐藏度量空间是双曲线的。拓扑和权重自然地作为双曲线度量属性的反映而出现。双曲线嵌入的一个共同目标是最大化双曲线网络模型的似然函数。困难在于似然函数是非凹的，难以优化。在本文中，我们提出了一种用于加权网络的双曲线嵌入方法。为了防止优化陷入众多的局部最优，初始嵌入是通过近似获得的。然后提出的梯度算法根据似然函数改进嵌入。在合成网络和真实网络上的实验表明，所提出的方法在不同的质量指标和应用方面实现了良好的嵌入性能。

I. INTRODUCTION

网络是描述离散对象之间关系的一般表示。大量的自然和人工系统以网络的形式构成。示例包括通信网络 [1]、生物交互网络 [2]-[4]、社交网络 [5] 和分布式系统 [6]-[9] 等。网络数据本质上是复杂的，在分析复杂的网络时，第一个挑战是找到一个有效的网络表示。

一直致力于开发网络嵌入技术，学习网络节点的向量表示。节点被编码成向量；网络中由边表示的关系由向量空间中节点之间的距离捕获。节点对之间的连接概率由度量距离确定。

在最近的研究中，越来越多的证据表明，许多现实网络的隐藏度量是双曲线的 [10]、[11]。实验结果表明，与嵌入欧几里得空间 [12]、[13] 相比，双曲线嵌入导致低失真。双曲几何的突出特点是双曲圆盘面积和圆长度随半径呈指数增长，为表示复杂的层次结构提供了更多空间[14]。双曲空间的几何性质保证了三角不等式，导致了聚类效应[11]，[15]。真实网络的无标度度分布和强聚类特性似乎是双曲几何基本特征的自然结果[15]。

大多数双曲线网络模型为网络拓扑提供了洞察力，然而，在现实世界中，网络不仅由其拓扑指定，而且由交互强度指定。连接必须与权重相关联才能完整描述网络。最近，已经发现了生物、经济和交通网络中权重的度量性质的证据 [11]；通过设计权重形成的概率机制，加权双曲线网络模型再现了真实加权网络的许多特性。

然而，在双曲生成网络模型中推断加权网络坐标的问题具有挑战性。我们证明了生成观察到的加权网络的双曲网络模型的似然函数是非凹的。为了解决这个问题，提出了一种双曲线嵌入的两阶段方法。第一阶段是通过近似找到初始嵌入坐标。第一阶段采用两种方法。一种利用谱嵌入，其目标与似然最大化相似；它将问题转化为可以得到理论解的优化。另一种方法使用贪婪启发式来产生次优嵌入。在第二阶段，通过似然函数的直接优化来改进嵌入；提出了一种基于梯度的方法来减少嵌入误差。我们使用不同的数据集研究嵌入方法的性能。对于合成网络，实验表明所提出的方法实现了更好的似然性和嵌入性能。对于真实网络，双曲线嵌入的表示具有保留节点相似性的能力，并在链路预测、节点分类和网络导航方面取得了良好的性能。

本文的主要贡献总结如下：

• 我们分析了生成双曲线网络模型的似然函数。我们证明了用于生成加权网络的双曲线网络模型的似然函数是非凹的。对于双曲线嵌入，这是第一个明确考虑权重生成过程的研究。嵌入是可解释的，并且能够保持加权网络中的节点相似性。
• 在分析生成双曲网络模型的基础上，提出了一种双曲网络嵌入方法。我们利用近似来找到网络的初始嵌入，并开发一种算法来改进嵌入。实验表明，所提出的方法在各种应用中取得了良好的性能。

II. R ELATED W ORK

网络嵌入将网络转换为低维空间，将有关网络的信息合并到嵌入向量中。传统方法基于摘要网络统计[16]和特征提取技术。这些方法通常涉及为特定任务设计的手工制作的功能，不能适应不同的应用程序。为了克服这些缺点，深度学习中的网络嵌入旨在通过数据驱动的方法学习网络表示。通过优化映射，学习空间中的几何关系反映了原始网络的结构。在这种情况下，已经开发出高效的网络嵌入技术，例如 DeepWalk [17]、Line [18]、图卷积网络 (GCN) [19] 和 GraphSAGE [20] 等。网络嵌入在深度学习中的概述可以是见[21]-[23]。

另一种网络嵌入方法是基于对复杂网络模型的研究。通过精心设计的机制，生成网络模型能够构建类似于真实网络的合成网络，具有广泛的结构特性。双曲网络模型具有产生与现实网络相似特征的网络的能力，受到了相当多的关注。证明[15]在双曲庞加莱盘中均匀分布的节点具有节点与其邻居连接的机制，生成具有无标度和聚类特征的网络。基于双曲生成模型，双曲嵌入是在双曲空间中推断最有可能重建网络的节点坐标。该概念进一步扩展到基于设计的目标函数的判别双曲线嵌入，以保持节点接近度[14]。

尽管双曲线模型表现出很好的特性来表征真实网络，但在双曲线几何中推断网络的坐标并非易事。双曲线嵌入的优化需要大量的计算工作。因此，嵌入结果通常是通过近似优化技术获得的。 Hypermap [24] 回放网络的双曲线增长：在每一步中，它通过最大化局部似然来找到添加节点的角坐标。 [25]中提出了一种社区检测算法来寻找节点的粗略布局。它使用最大似然估计来获取精确位置。 [26]中提出的算法使用公共邻居的数量来推断角度坐标。变体 [27] 通过仅通过公共邻居推断高度节点的坐标来提高效率：根据启发式策略贪婪地放置低度节点。该研究[28]提出了一种基于平铺的双曲线嵌入数值稳定性模型。在最近的一项研究中，双曲线嵌入进一步扩展到能够保留语义信息的异构信息网络（HIN）[29]。另一类双曲线嵌入算法基于一种称为“角合并”的现象[30]。节点角坐标可以通过根据节点聚合模式 [30]、[31] 的流形机器学习嵌入来近似。

大多数现有的双曲线嵌入算法都是基于未加权网络的。在最近的研究中，基于流形机器学习的算法被扩展到加权网络的嵌入[30]。然而，如果没有链接和权重生成机制，嵌入是不可解释的。通过生成双曲线网络模型，所提出的嵌入可以解释为：角度差异反映节点的相似性；节点度用径向坐标表示；边缘的可能性及其权重可以通过双曲线距离来估计。该特征对于基于双曲线嵌入的许多应用的社区检测、链路预测、网络路由和理论分析是必不可少的。

III. PRELIMINARIES

在本节中，我们简要介绍[11]中提出的符号和加权双曲线网络模型。我们将此部分限制为仅介绍基本双曲线网络模型的细节。全面介绍，读者可参考文献[11]、[15]、[32]。

A. Notation

我们遵循网络理论的标准符号和定义，并考虑加权无向网络 G 1/4 ðV； EÞ，其中 V 1/4 v1； . . . ; v N 是包含 N 个顶点的顶点（节点）集。 E 是边集。 E 的每个元素 e ij 表示 vi 和 vj 之间的无向边，具有相关的权重 w ij 。我们将 G 的邻接矩阵定义为 A 1/4 1/2a ij 2 RðN NÞ，其中 a ij 1/4 w ij 如果 e ij 2 E 否则 aij 1/4 0。 D 是对角矩阵，其中 Dii 1/4 Pj a ij。

B. Weighted Hyperbolic Network Model

几何网络模型定义了网络集合上的概率分布，这些网络是用概率随机生成的。在权重几何网络模型中，N个节点均匀分布在一个K维均匀各向同性度量空间中。根据概率密度函数 (pdf) rðkÞ，为每个节点分配一个隐藏变量 k。连接概率 pðk； k0;两个节点的 dÞ 是其隐藏变量 k 的函数； k0 和距离度量。具体来说，

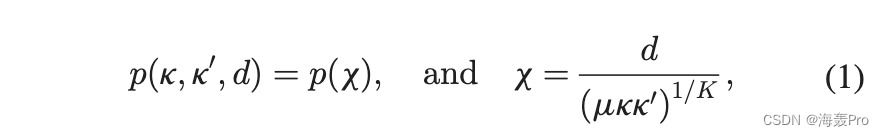
其中 m 是与生成网络中的平均度相关的正自由参数。 pðxÞ 是一个任意正函数，取值来自 (0, 1)。

为了生成加权网络，分配给每个节点的另一个隐藏变量 sis。具有隐藏变量 k 的两个节点之间现有链接的权重； k0;小号； s0 和距离 d 由下式确定

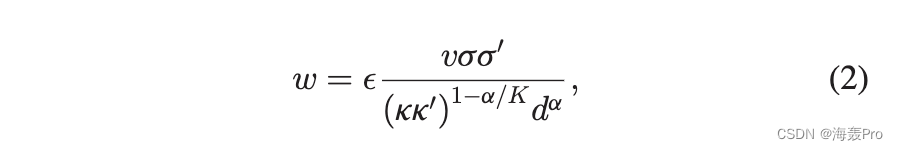
其中 0 a < K 控制权重和基础度量空间之间的依赖关系 [11]。 v 是决定网络平均强度的正参数。是具有概率密度函数 fð Þ 的正随机变量。

该模型生成的网络具有几个属性[11]。每个节点的期望度 k 与其隐藏变量 k 成正比；可以选择参数 m，使得 kðkÞ 1/4 k。类似地，可以选择参数 v 以确保节点 s 的预期强度等于变量。这些关系独立于连接概率 pðxÞ 和噪声分布 fð Þ 的特定形式。根据上述属性，分别由 k 和 s 指定的节点度和强度可以独立配置。

我们考虑一个特定模型，其中基础几何是半径为 R 1/4 N=2p 的圆 S1，其中 N 个节点均匀分布。角坐标 u 确定几何空间中的节点位置。节点之间的距离 d 是根据弧长测量的。连接概率设置为 pðxÞ 1 1þx b ，其中 b 是调整网络聚类系数的参数。为简单起见，我们假设权重的乘性噪声服从指数分布，平均 h i 1/4 1。为了获得具有无标度度和强度分布的网络，变量 k 和 sare 根据幂律分布 rðk 进行采样； sÞ 1/4rðkÞrðsjkÞ, k0 < k < kc

上述模型等价于嵌入恒曲率双曲平面的 H2 模型 1 [11]、[15]。 S1模型中的隐藏变量k可以映射到径向坐标r

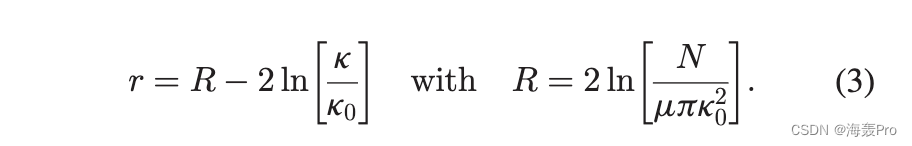
角坐标 u 在 H2 模型中保持不变。 s 是决定节点强度的参数。连接概率可以写为

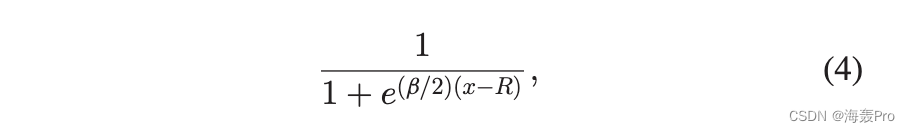
其中 x 是节点之间的双曲线距离。极坐标下两点之间的双曲线距离 x d； uÞ 和ðr0; u0 Þ 由余弦双曲定律给出

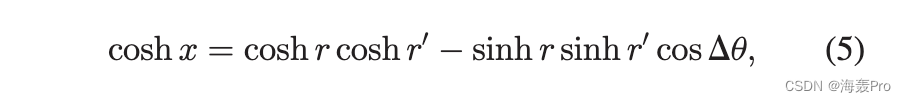
其中 Du 是点之间的角度。对于较大的 r, r0 和 Du > 2 ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffie r + e r0 p 时，距离可以近似为 x 1/4 r + r0 + 2 ln Du2。因此，权重可以表示为

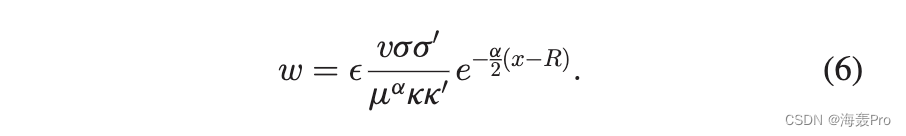
为了统一参数表示，除非另有说明，我们在本文中使用 S1 模型表示。

IV. H YPERBOLIC E MBEDDING OF WEIGHTED N ETWORKS

双曲线嵌入是生成的逆过程。给定网络结构和权重，双曲线嵌入的目标是推断网络的隐藏变量，即节点角坐标 u 和变量 k 和 s。由于网络被认为是由概率模型生成的，因此推断网络参数的自然解决方案是使用可能性来评估嵌入质量。根据双曲网络模型，生成网络拓扑的对数似然表示为

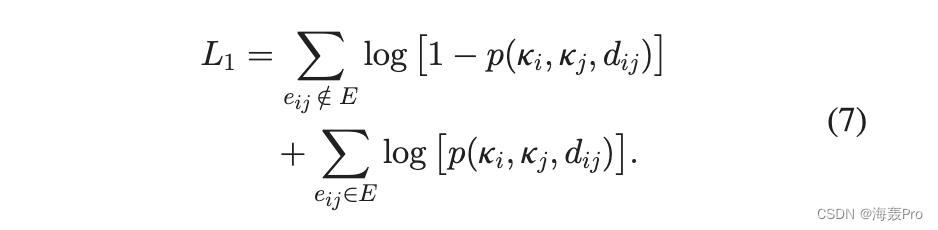
连接节点 i 和 jis 1 w ij fðwij wijÞ 的现有链接权重的 pdf，其中 w ij 1/4 vsisjðkikjÞ1 a=K daijand w ij 是实际权重。生成权重的对数似然由下式给出

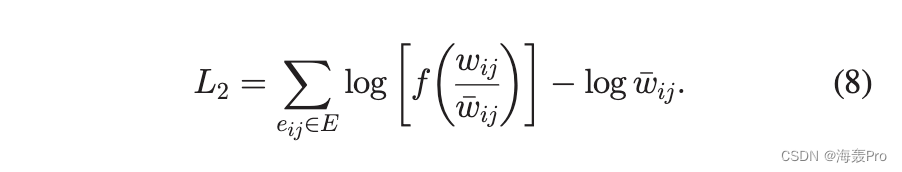
双曲线嵌入可以被认为是寻找最大化似然函数的参数的优化问题。下面，我们从理论上分析优化的难度，以表明将网络嵌入双曲空间是具有挑战性的。

命题 1：给定一个网络 GðV； EÞ，加权双曲线模型 L1 和 L2 的对数似然函数相对于参数 u 不是凹的。

证明：我们首先证明对数似然函数 L1 是非凹的。考虑两种情况。

在第一种情况下，网络 G 是全连接的，L1 仅包含等式 7 中的第二项。为简单起见，我们假设 ki 等于所有节点的固定常数 C，并且 ui 1/42pi N 1 , i 1/4 1个； ; N 1. 由于 ui 在 1/20 上等距分布； 2pÞ 和节点变量值相等，节点 i 1/4 1 的过程可互换； ; N 1. 在这种情况下，L1 是 u0 的周期函数。我们可以验证 L1 对于不同的 u0 是非常量的；因此，当网络全连接时，L1 不是凹函数。

对于非全连接图，存在节点对 eij =2 E。我们可以证明 limDuij!0 L1 1/4 1 并且因此 L1 不连续。因此，L1 不是凹函数，我们可以得出对数似然函数 L1 是非凹函数的结论。

我们接下来证明对数似然函数 L2 也是非凹的。我们假设节点对 e ij 2 E, limDuij!0 w ij 1/4limd!0vsisjðkikjÞ1 a=D da 1/4 1;因此，limDuij!0 L2 1/4 1. 使用与 L1 的第二种情况相同的推论，L2 不是凹函数

该命题表明加权双曲线网络模型的似然函数不是凹的。使用局部方法优化这样的目标函数会导致收敛到局部最优。为了说明这个问题，让我们考虑一个在优化过程中可能遇到的例子。

我们考虑针对 u 优化 L1，并假设 k 值是完全已知的。我们对这个优化问题使用梯度法。通过梯度法，参数向量朝着优化函数增长最快的导数方向移动。不失一般性，我们考虑具体节点i； L1 对 ui 的导数是

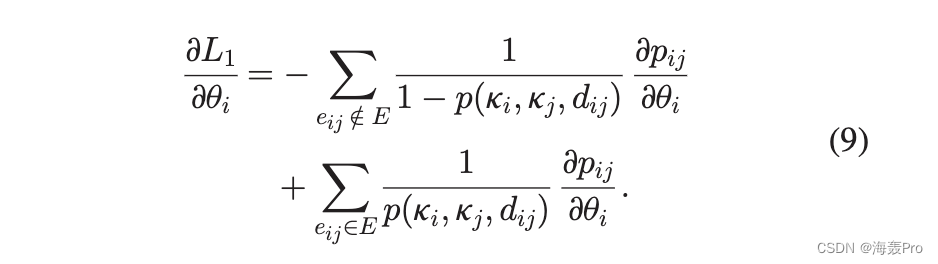
对于连接到节点 i 的节点，为了增加可能性，将 ui 调整为减小它们的角度 Du 差异的方向。相比之下，对于未连接到节点 i 的节点，调整 ui 以增加 Du。直观地说，连接的节点相互吸引，未连接的节点相互排斥。每个节点的角度是随机初始化的，并且在 1/20 上服从均匀分布； 2pÞ（见图 1）。节点根据梯度调整它们的角度，直到达到稳定的配置。由于节点均匀分布在一个圆上，由于对称性，节点上的预期力为零；随机配置导致节点不调整参数以改善嵌入的稳定状态。

图 2 显示了合成网络的调整值@L1@u，以最大化优化中的可能性。 u 随机初始化并以不同的步长进行调整。当步长较小时（图 2a），优化很快收敛到一个稳定的配置，这也几乎是随机的。在图 2b 中，步长是第一种情况的 200 倍。更新变得不稳定； u 偶尔会被较大的值调整，优化不会收敛。局部优化方法的直接应用是不可行的，这会导致收敛性差的双曲线嵌入或优化不稳定。

大量局部最大值广泛分布在可行域中，其中只有少数具有可接受的嵌入性能。一个好的起点可以防止优化陷入局部最大值，并且可能对进一步优化很重要。

V. APPROXIMATE SOLUTION OF HYPERBOLIC E MBEDDING

最大似然估计的目标不是凹的，这使得问题难以优化。为了找到合适的嵌入，一种解决方案是采用简化原始问题的近似技术。具体来说，我们可以优化一个不同的相关目标，其中优化更容易解决，或者采用启发式策略来产生次优嵌入。为了找到网络的初始嵌入，我们介绍了两种方法。

A. Spectral Method

一类双曲嵌入算法可以归类为基于流形学习的方法。节点角坐标可以在流形学习的嵌入空间中直接近似。在特殊情况下，此类方法通过特征分解 [30]、[33] 遵循欧几里得空间中的谱方法。

关于双曲线网络模型的一个基本观察是节点之间的连接概率与角度差负相关。应为连接的节点分配相似的角度以增加可能性。在启发式之后，可以通过拉普拉斯矩阵定义不同的目标。拉普拉斯矩阵是由 L 1/4 D A 给出的相邻矩阵 A 的变换。

我们将 Y 定义为 N 2 矩阵，其中每一行代表欧几里得空间中节点的坐标。拉普拉斯矩阵的一个基本性质是 trðY T LY Þ 1/4 Pi;j a ijkY i Y jk2。轨迹是相邻节点之间距离的加权和；最小化轨迹会减少连接节点之间的欧几里得距离。如果节点分布在以原点为中心的圆周附近，则欧几里得空间中的距离也反映了角度差异。包含一个附加约束 Y T Y 1/4 I 以避免任意缩放。优化问题可以表述为

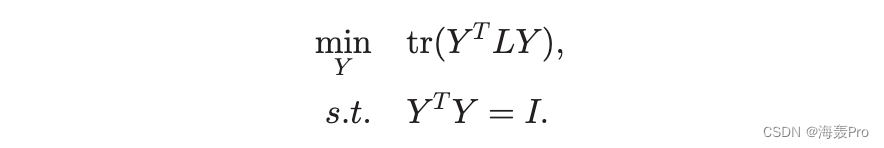
根据 Rayleigh-Ritz 定理，这个问题的解由对应于拉普拉斯矩阵的最小非零特征值的两个特征向量构成。原问题中节点的角坐标可以近似为角度 u 1/4 arctan y2y1 ，其中 y1 和 y2 是 Y 中与节点对应的行向量的第一个和第二个条目。通常，需要一个额外的等距调整步骤来将节点均匀地分布在一个圆上[30]。

除了拉普拉斯谱之外，模块化矩阵 B [34] 可以形成类似的目标。该问题可以表述为最大化迹线 trðY T BY Þ。与拉普拉斯情况相反，解对应于具有最大特征值的模块化矩阵的两个特征向量。图 3 绘制了使用拉普拉斯和模块化谱的角度估计。这两种方法都为节点角度提供了良好的嵌入性能。然而，我们发现拉普拉斯谱提供了更好的估计；当使用不同配置的双曲线网络模型时，也得到了类似的结果。因此，我们使用拉普拉斯谱近似作为节点角度的初始嵌入。

为了推断参数 k 和 s，节点的实际度数 k 和强度 s 用于初始值。

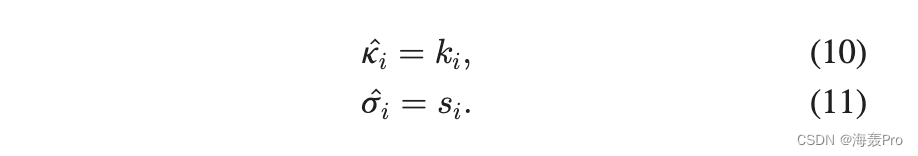
网络的频谱通常与社区检测方法有关。由于双曲嵌入的角度可以通过拉普拉斯和模块化矩阵的谱来近似，因此节点角度和网络社区之间可能存在相关性。第八节实验验证了相关性的存在

B. Greedy Strategy

另一种有效的双曲线嵌入方法是采用贪心策略。与同时针对所有变量的优化相比，变量的顺序优化相对简单。因此，贪心方法一次推断一个节点的参数，考虑到只有已经嵌入的节点的可能性。在本小节中，我们回顾了一种贪心算法来嵌入具有拓扑信息的网络 [27]。

网络核心（大度节点）是通过使用公共邻居的数量来嵌入的。两个节点的共同邻居的预期数量是它们在双曲平面中的位置的函数。两个节点的角度差的最大似然可以由下式获得

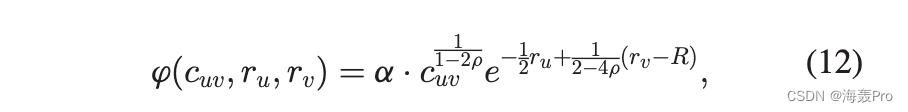
其中 c uv 是公共邻居的数量。 r u 和 r v 是双曲平面中的节点径向坐标。 r 是与度数分布的幂律指数相关的参数，使得指数 g 满足 g 1/4 2r + 1。R 是确定最小度数的参数（等式 3）。

大度节点的成对角度差可以通过上式计算。基于成对角度差异，可以采用弹簧嵌入或球形多维缩放[35]来获得实际角度。

对于小度数的节点，节点按度数降序嵌入；度数大的节点具有较高的嵌入优先级。计算所有邻居角度的加权平均值以近似特定节点的角坐标。得到的角度通常接近于达到最大局部似然的角度。为了改进嵌入，随机采样角度周围的 Oðlog ðNÞÞ 点；该节点被分配产生最大可能性的角度。

VI. OPTIMIZATION OF THE M AXIMUM L OG-L IKELIHOOD

近似方法降低了解决嵌入问题的难度；但是，被忽略的信息可能会引入额外的错误。误差源于逼近导致的目标不一致、贪心策略的累积偏移量和估计量的方差。由于估计误差是近似的固有特征，因此通过近似方法本身可能难以减少误差。为了提高嵌入性能，我们重新审视了对数似然的优化。在本节中，我们提出了一种基于梯度的方法来改进嵌入。在介绍该方法之前，需要导出似然函数对每个变量的导数。

不失一般性，我们考虑特定节点 i 的参数梯度。 x i 表示可以是 ki、si 或 d ij 的变量。 L1 相对于 x i 的梯度可以表示为

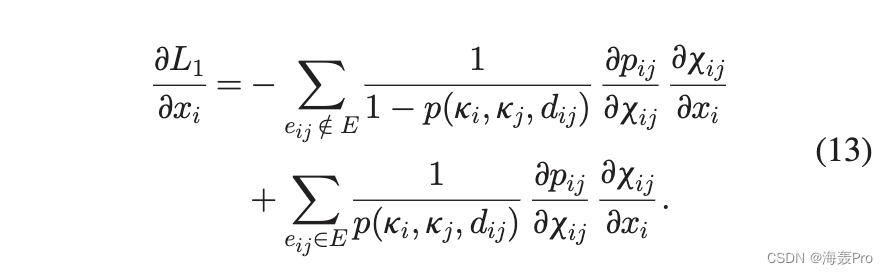
将 pðxijÞ 1/4 1=ð1 þ x bijÞ 和 xij 1/4 dij =ðmkikjÞ 代入上式得到

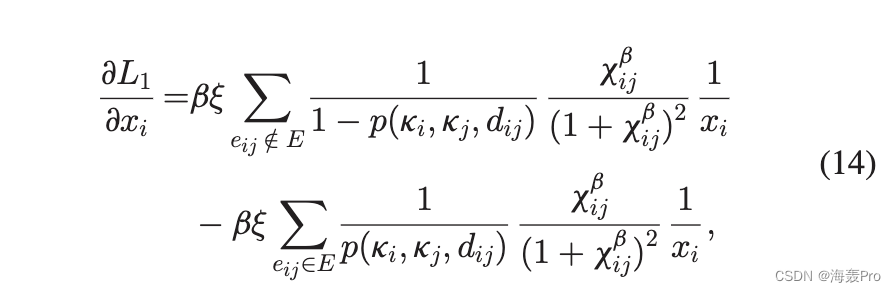
哪里是 x i 在 d ijmkikj 中的幂指数。我们注意到 x bij1þx bij1/41 p ij，所以上式可以简化为

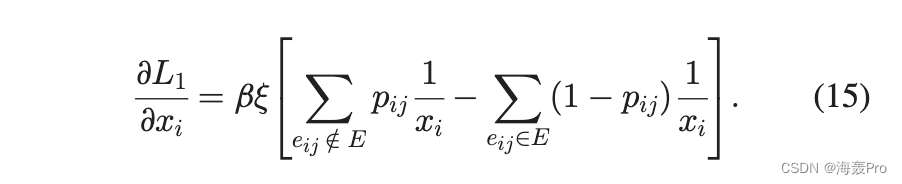
类似地，我们可以得到 L2 的梯度为

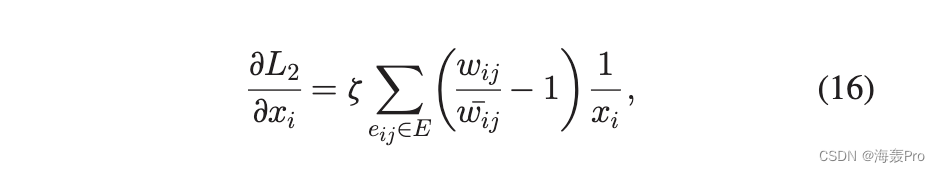
其中 z 是 x i 在 w ij 中的幂指数

要计算 @L@ui 1/4 @L@d ij@d ij@ui ，我们需要推导出 @d ij@ui 。由于 d ij 是半径为 R 的圆中两个节点的弧长，因此 d ij 1/4 Rduij 1/4 Rðp jp jui ujjjÞ，@d ij@ui 根据相对位置只取 R 或 R 两个值节点 i 和 j。

我们可以通过将 x 替换为相应的变量来获得对双曲网络模型的任何变量的导数，因此可以应用标准梯度上升来提高嵌入性能。然而，将梯度法应用于优化时会出现潜在的稳定性问题。合适的步长可能因不同的变量而异。为了保持优化的稳定性，应该为角坐标设置一个小的步长。然而，相同的步长对于其他参数的有效更新来说太小了。此外，对数似然对 u 的导数是无界的。如果距离 d 接近 0，则梯度可能会爆炸并导致不稳定。

为了规避上述问题，对变量 s、k 和 ua 依次进行优化，并以不同的步长进行更新。我们对角坐标使用较小的步长，对参数 s 和 k 使用较大的步长。为了避免爆炸梯度，每次更新都被限制在一个指定的范围内。为每个变量设置一个阈值；如果更新超过阈值，我们会裁剪梯度。

这些策略在稳定优化方面是有效的；然而，优化在几次迭代后陷入局部最优，阻碍了嵌入质量的进一步提高。我们期望目标函数在原始曲面的基础上更加平滑，以反映目标的趋势。因此，我们需要一个优化问题的新公式，其中目标具有较少的局部最优值并且更容易优化。

为了实现这一目标，调整值使用少量参数进行参数化，从而减少变量的维数。具体来说，我们假设角度调整值由 continue 函数 fðujy1 确定； ; y nÞ 由 n 个参数 y1 参数化； ;是的； 0 u < 2p，并且 limu!0þ fðuÞ 1/4 limu!2p fðuÞ 1/4 fð0Þ（参见图 4）。对于每个节点，根据函数值 fðuÞ 调整角度。新角度由下式确定

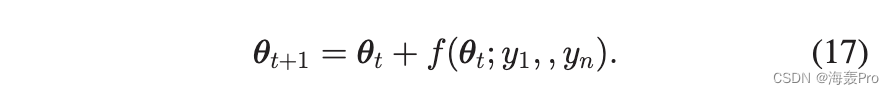
为方便起见，上式写成向量形式，其中uut和uut+1分别表示当前角度向量和调整后的角度向量。 f 是一个元素函数，适用于向量 uu… 的每个元素。

通过参数化调整，embedding优化变成找到一组参数y1； ; y n 最大化对数似然：

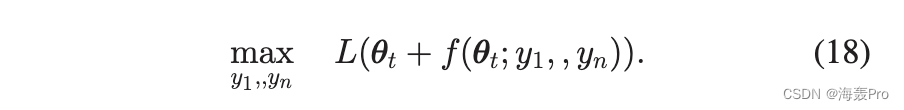
优化目标函数，一个基本问题是确定参数化调整函数的参数个数。选择参数个数有两种极端情况。一端，n大于等于节点数；每个节点的角度调整是独立的；该方法相当于标准梯度上升法。另一端，参数个数n等于1；在这种情况下，所有节点都旋转相同的角度，这不会影响嵌入结果。介于两者之间的是实践中使用的中间方法。由于 n 通常小于节点数，因此陷入局部最大值的概率会降低

可以选择不同形式的函数来参数化调整值。例如，可以很容易地采用输入域为单位圆的神经网络。但是，为简单起见，我们使用分段线性插值函数，其中1/20； 2pÞ 被平均分为 n 段。每个段的端点可以独立改变；每个段内的调整值是端点的插值。图 5 显示了 20 段的插值函数。

为了导出参数的梯度，我们将分段线性插值改写为

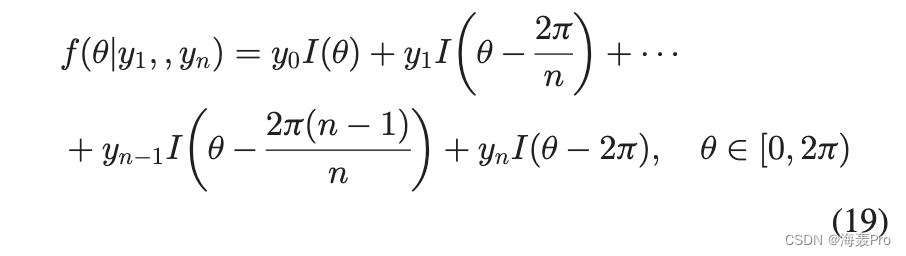
where

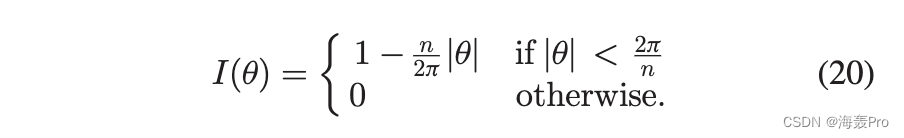
和 y0 1/4 y n。似然函数关于第 k 个参数 y k 的梯度可以表示为

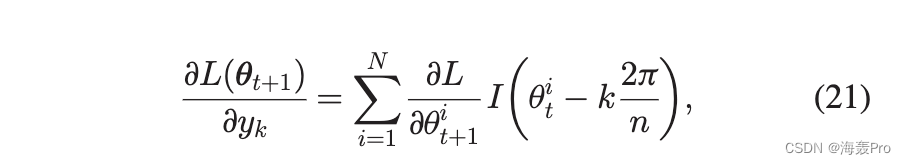
其中 ui t 是向量 uut 的第 i 个元素。梯度是由函数 I 加权的导数之和。考虑到第 k 个端点附近的所有节点，参数 y k 在总影响方向上变化。角度调整不仅取决于节点自身的导数，还取决于所有附近节点的导数，即角度调整在具有相似角度的节点上泛化。

在实践中，参数 y1； ; y n 被初始化为小的随机数。我们用不同的步长依次更新变量。采用动量梯度上升法加速优化。调整后的变量具有完全的自由度，每个变量都可以独立改变；我们使用前面提到的梯度方法来微调嵌入。

VII. COMPLEXITY ANALYSIS

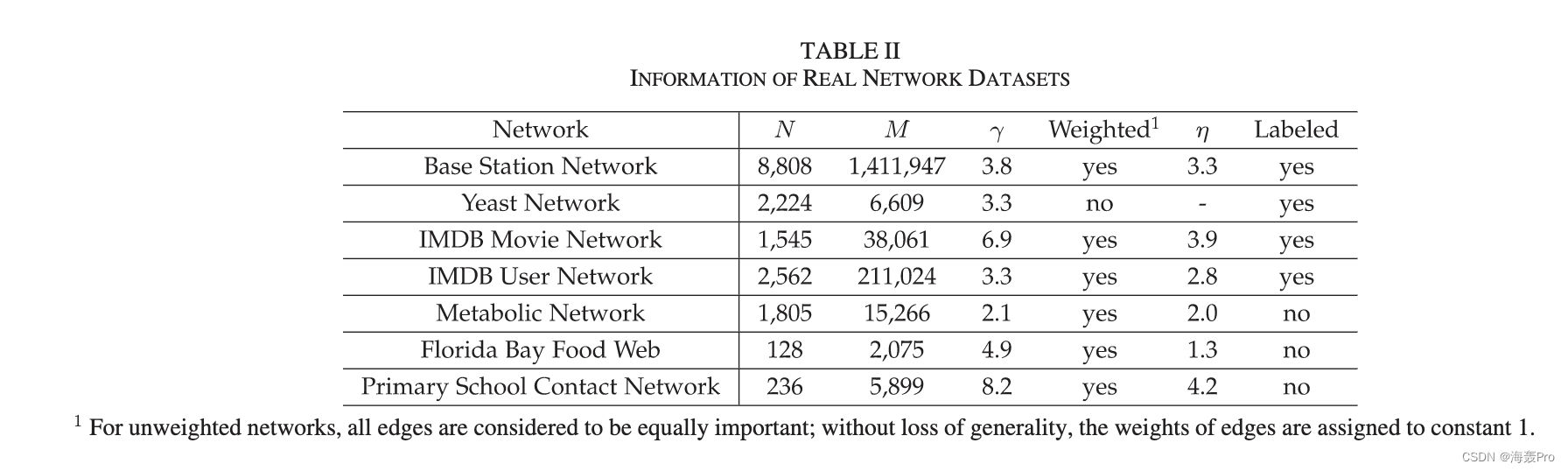
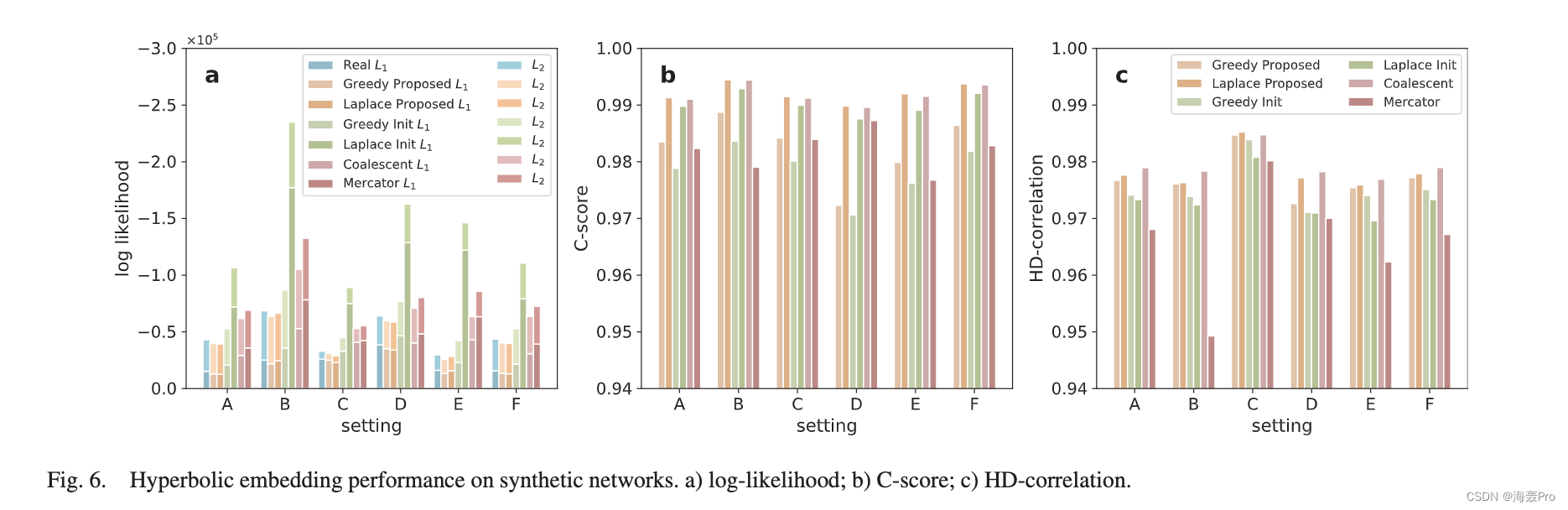
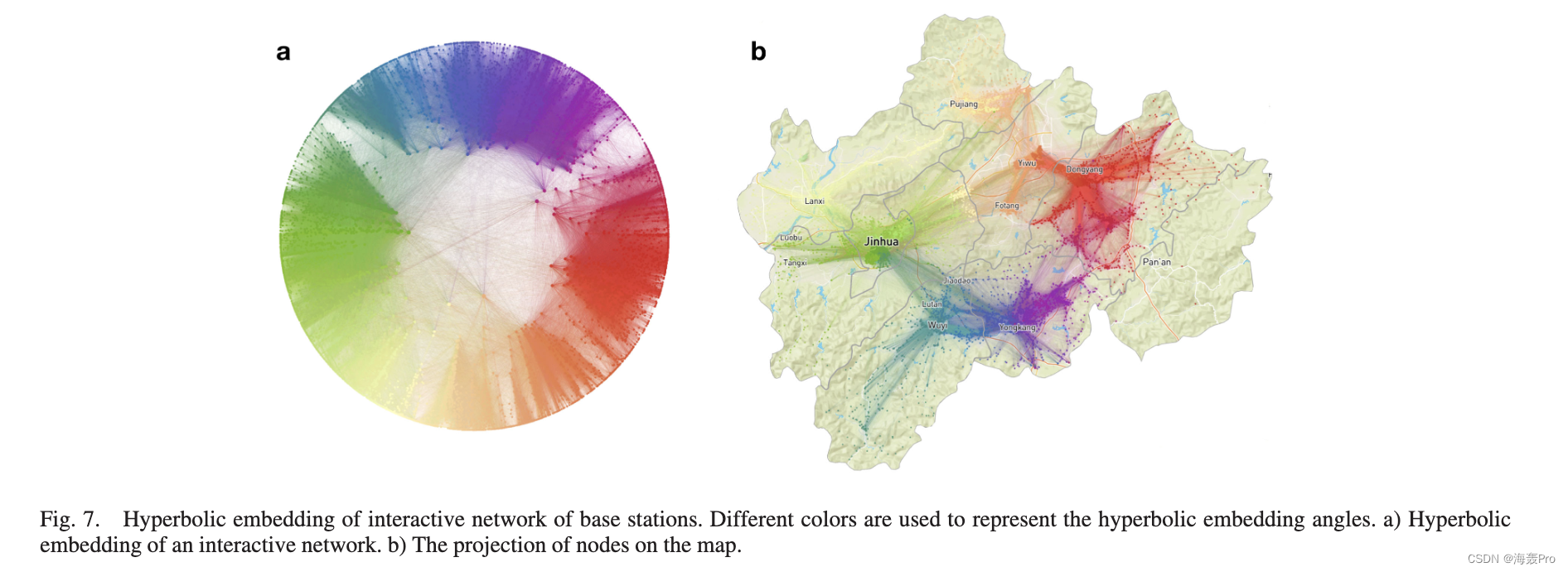
VIII. E XPERIMENTAL RESULTS

结语

文章仅作为个人学习笔记记录，记录从0到1的一个过程

希望对您有一点点帮助，如有错误欢迎小伙伴指正