@TOC

简介

Hello！
非常感谢您阅读海轰的文章，倘若文中有错误的地方，欢迎您指出～
 
ଘ(੭ˊᵕˋ)੭
昵称：海轰
标签：程序猿｜C++选手｜学生
简介：因C语言结识编程，随后转入计算机专业，获得过国家奖学金，有幸在竞赛中拿过一些国奖、省奖…已保研
学习经验：扎实基础 + 多做笔记 + 多敲代码 + 多思考 + 学好英语！
 
唯有努力💪
 
【每日一读】每天浅读一篇论文，了解专业前沿知识，培养阅读习惯（阅读记录 仅供参考）

论文简介

原文链接：https://link.springer.com/article/10.1007/s10489-021-02498-w

期刊：Applied Intelligence （CCF C类）

年度：2021年5月24日（发表日期）

Abstract

属性网络嵌入能够通过利用网络结构和属性数据生成网络对象的低维表示

然而，如何恰当地组合两个不同的信息以实现更好的向量表示仍然不清楚

有些方法分别从图结构和属性数据中学习嵌入信息，然后将两者结合起来，而有些方法则将属性数据作为辅助信息

然而，由于属性空间的稀疏性，将属性数据集成到嵌入过程中是一个开放的问题

特别是在Twitter和Flickr这样的社交网络中，上下文可能很短，定义对象的属性数量很少，这导致对象之间的上下文邻近性没有被很好地发现

为了解决这些问题，在这项工作中，我们提出了一种增强的属性网络嵌入方法，通过丰富的属性表示(ANEA)生成网络对象的低维表示

• ANEA通过将数据映射到两个不同的图结构，将属性数据合并到嵌入过程中
• 为了解决稀疏性问题，我们的方法通过在这些图上执行随机游走来捕获属性之间的高阶语义关系
• ANEA通过一个由网络结构和属性组成的联合空间来学习嵌入。因此，它可以发现对象的潜在属性表示，这有助于解释在节点之间的邻近性建模中，哪些共同的上下文兴趣是有效的

在真实网络上的实验证实，ANEA优于最先进的方法。

1 Introduction

属性网络被广泛观察到在许多不同的领域，从传播学到生物学，如引文网络，社会网络，通信网络和生物交互网络。近年来，对这些网络的分析在许多领域都引起了极大的关注，例如旨在寻找用户和商品之间潜在联系的定向广告，以及旨在达到特定消费者受众的推荐系统。为了让这些系统更好地预测和聚类用户、项目或连接，他们在网络数据上应用了一些机器学习模型。然而，由于属性网络可以被建模为图，其节点代表网络对象，边代表这些对象之间的关系，因此没有一种直接的方法可以通过保留网络中对象的全局位置来将网络结构合并到机器学习模型中。

近年来，网络嵌入方法被提出来生成低维表示，其中网络上高度接近的节点具有相似的向量表示。这些方法力求通过保持网络的全局和局部结构来恰当地模拟节点之间的接近性。与仅由节点依赖组成的普通网络不同，在属性网络中，每个节点还与定义对象的属性集相关。传统的网络嵌入方法忽略属性信息，只考虑网络结构[9,19]。最近，一些方法关注于提高网络嵌入方法的性能，考虑到节点的属性[21,28,31]。网络嵌入的两种主要方法是基于矩阵分解的模型[10,31]和基于随机游走的模型[26]。基于矩阵分解的方法是通过挖掘节点间的一阶和二阶关系来分解图的邻接矩阵，基于随机游走的方法是通过节点间的移动来提取图的高阶关系。然而，网络通常是大规模的例子，其拓扑(即邻接矩阵)相当稀疏。因此，随机游走方法通过将图结构转化为固定长度的结构化序列，缓解了稀疏性和维数诅咒问题，在网络嵌入中得到了广泛的应用。然而，该方法提出了一个新的挑战，即如何在考虑属性上下文的属性网络上有效地执行随机漫步。

现有的基于随机游走的方法通常使用属性数据作为辅助信息，对具有公共属性的节点之间的接近度进行建模。然而，一些现实世界的网络具有相对较低的同质性程度，这表明节点并不倾向于与它们的邻居处于同一集群中。因此，从图结构中获得的随机游走可能不足以有效地建模节点的近性。在这种情况下，在计算节点之间的接近性时，属性接近性成为更重要的因素。探索节点之间的属性接近性是一项特别具有挑战性的任务，因为网络中的属性通常是稀疏和不完整的。这种情况导致现有的嵌入方法在现实网络中的性能会大大下降[13,15]。

而且，大多数基于随机游走的嵌入方法并没有提供哪些潜在利益触发了节点之间的交互以及节点之间的上下文相似性或差异[23]。对每个节点或节点组的上下文表示进行特征化是解释两个节点之间存在高低上下文邻近性的原因，揭示网络中哪些相似的利益导致了一个群体的形成的重要途径。本文提出了一种新的属性网络嵌入模型(ANEA)，该模型通过在图嵌入过程中加入丰富的上下文维来学习低维节点嵌入。为了创建属性图的上下文维度，我们将属性数据转换为两种不同的图结构:二部图和共属性图。这些图分别包含属性和节点之间的关系，以及属性之间的共现关系。该方法在结构图和上下文图上进行联合随机游动，并利用跳跃格模型学习统一空间。

---

我们将本文的贡献总结如下:

• 我们提出了一种新的属性网络嵌入算法ANEA，该算法通过将丰富的上下文信息集成到结构信息中来学习节点的低维表示。
• ANEA旨在通过发现上下文图上属性之间的高阶语义关系来丰富节点的属性表示。因此，可以通过语义相关的属性更有效地建模没有公共属性但属于同一类的节点之间的接近性，这也缓解了稀疏性问题。
• ANEA同时生成节点表示之外的上下文表示，允许我们解释哪些属性在建模节点之间的亲和性时具有很高的影响。此外，ANEA使我们能够创建查询，以发现与一组查询节点和查询属性相关的社区
• 在5个真实网络上进行了实验，以评估所提出的嵌入模型的有效性，该模型考虑了不同类型的网络分析任务，如节点分类、网络可视化和定性分析查询。实验结果表明，该方法明显优于现有方法。

2 Related work

为了促进许多网络任务，如节点分类、链接预测和网络可视化，许多工作集中于为网络对象生成有意义和有效的低维表示。近年来，研究人员提出了许多网络嵌入方法，也称为网络表示学习。现有的研究主要分为两个分支:基于结构的嵌入方法和基于属性的嵌入方法。

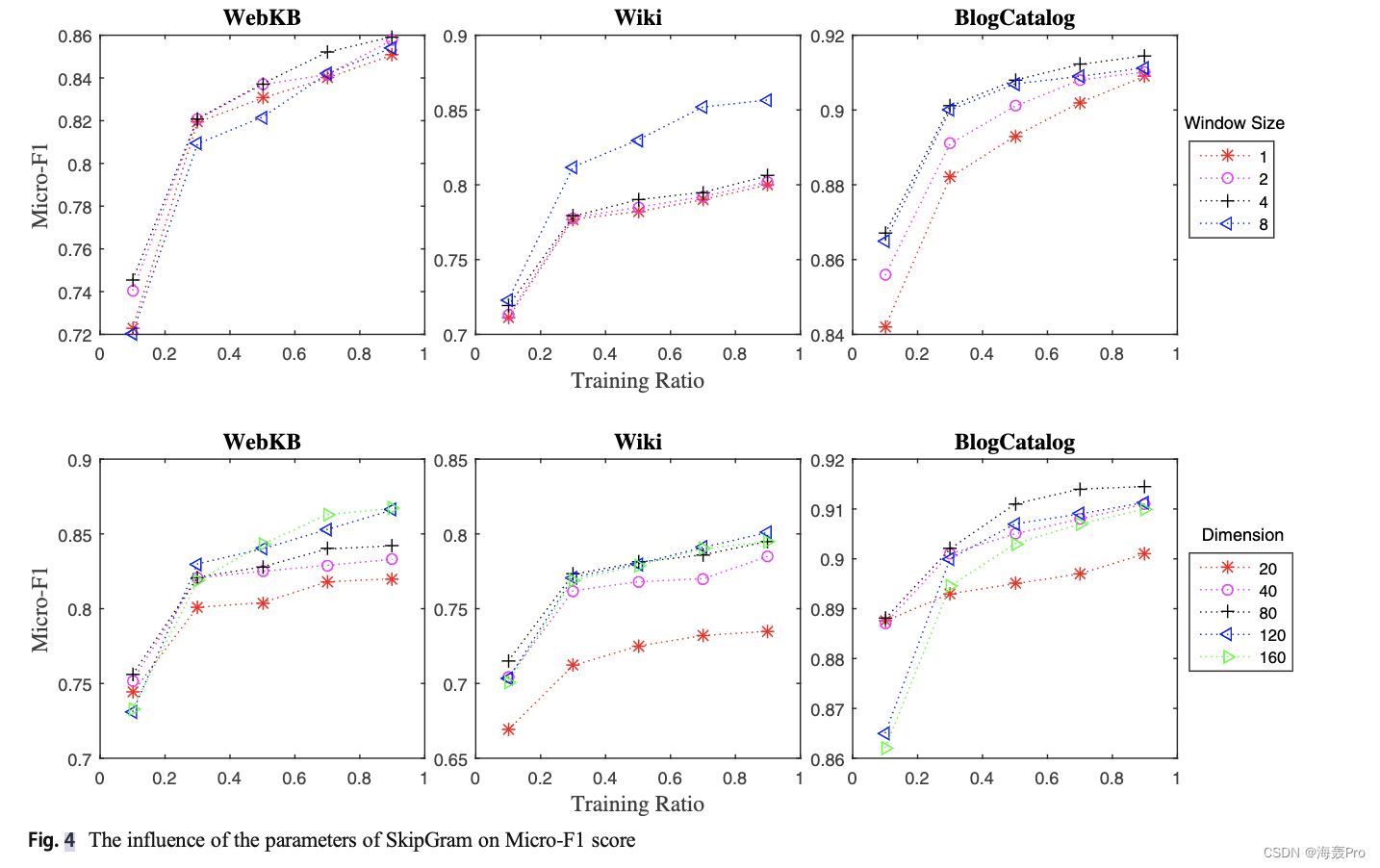
基于结构的方法旨在保持网络中节点的局部和全局结构近性。第一个例子是DEEPWALK[19]，它结合了随机漫步方法和SkipGram神经网络模型[17]。在自然语言处理中，使用SkipGram算法学习单词的低维嵌入，以发现文本语料库中观察到的单词之间的语义关系。DEEPWALK受这种词嵌入方法的启发，利用从图中获得的节点序列，在固定长度内进行随机游走，而不是单词序列。由于DEEPWALK具有高度的有效性和可扩展性，该模型率先增强了许多不同的网络嵌入方法[9,25,26]。NODE2VEC[9]执行广度优先搜索和深度优先搜索算法，获得一阶和二阶随机漫步。类似的，LINE[25]的目标是利用边缘采样算法捕获网络中的一阶和二阶近性。GRAREP[3]在迭代过程中使用矩阵分解技术获得不同的节点表示，提取节点的不同局部信息。然后，它将这些表示连接起来，以获得节点的全局表示。SDNE[26]通过应用多个非线性映射函数来利用图的非线性结构信息。

上面提到的基于结构的嵌入方法忽略了属于节点的标签和文本内容等属性信息。然而，最近的研究表明，属性对于有效地模拟节点之间的邻近性非常有帮助，特别是当网络是稀疏连接的，且网络中存在断开连接的节点时[11,16]。为了充分利用丰富的属性信息，[28]提出了TADW框架，该框架通过定义和分解文本相关矩阵，将文本数据集成到嵌入阶段。TADW在基于svd的矩阵分解框架下学习节点嵌入。由于矩阵分解阶段既耗时又消耗内存，TADW不能扩展到大型数据集。此外，TADW利用一个近似矩阵，因为分解一个精确的矩阵是一个困难的过程。因此，TADW产生相对较差的节点表示，尽管它实现了比结构方法更好的性能。另一个开创性的研究是TRIDNR[18]，它使用三种不同类型的信息学习节点的嵌入:图结构、文本内容和节点标签。TRIDNR通过执行DEEPWALK和DOC2VEC[5]方法分别从这些不同的来源生成低维向量表示，然后以迭代的方式将它们线性组合。因此，在学习阶段，在这些独立的模型之间转移知识是不可能的。这意味着在建模节点接近性时，网络结构和节点属性互不影响。TENE[31]和FSCNMF[1]以类似的方式分别对图的结构和文本信息进行建模，并将这两个模型结合起来获得联合节点嵌入。与TADW方法不同的是，这些方法将嵌入任务表述为联合非负矩阵分解。FSCNMF将上下文信息作为属性矩阵集成到学习过程中，而TENE通过发现节点的文本集群成员关系在集群级别使用属性数据。然而，这两种方法考虑了一阶和二阶节点和属性的近性，因为它们将结构和上下文信息作为矩阵的形式处理，即邻接和属性矩阵。AANE[10]旨在使用对称矩阵分解方法学习基于属性分解和节点接近性的联合嵌入表示。该算法采用分布式优化算法，将问题分解为多个子问题，以降低问题的复杂度。它与TENE和FSCNMF具有相同的局限性，因为AANE使用属性数据作为成对的相似矩阵。

不同于在欧氏空间设计的其他方法，BANE[30]学习低维二进制节点表示，以减少存储和计算成本。该方法综合了节点的邻域信息和属性信息。BANE的学习过程依赖于对邻接矩阵和属性矩阵的乘积进行因式分解。然而，BANE在处理短二进制代码时可能会丢失大量信息。

除了学习矩阵分解框架下的节点嵌入方法外，也有一些研究工作旨在考虑节点丰富的上下文信息，增强基于随机游走的图嵌入方法。GAT2VEC[21]方法与我们的方法最相似，它将属性数据作为辅助信息加入到网络嵌入过程中，学习节点嵌入。该方法通过在二部图上执行随机漫步生成节点-属性序列，其中每个节点只与自己的属性相连。该方法旨在提高具有共同属性的节点之间的亲和度。我们的工作和GAT2VEC之间的一个关键区别在于，考虑到高阶邻域的属性，我们的工作具有高阶邻域的属性，我们的工作具有高阶邻域的属性，我们的工作具有高阶邻域的属性。[32]中的作者提出了SEANE框架，该框架通过向网络结构中添加属性来构建混合图结构。它采用了一种考虑到节点之间相似性的受限随机游走抽样。TNE[23]在基于随机游走的嵌入过程中增加了一个主题模型[2]，以捕获节点之间的主题级语义交互。该模型为每个节点生成主题分布，为每个主题生成单词分布。TNE允许生成基于节点和上下文的表示，但它需要优化两个不同的目标函数。

3 Problem definition

如前几节所讨论的，获得属性网络的有效表示的方法是利用网络结构和属性数据

然而，在属性网络中，属性空间总是稀疏的，有些节点的属性非常少，有些属性只对单个节点可用

例如，在Twitter和Flickr等社交网络中，属于网络对象的文本信息通常很短。然而，我们知道，有些词的表现形式不同，但语义相似。在这个方向上，发现属性之间的语义关系允许我们正确地上下文表示每个对象。在本文中，我们假设将属性之间的多个不同程度的相似度整合到嵌入过程中可以改善表示学习

为了实现这一假设，我们建议在结构图之外使用上下文图，将属性数据转换为两种不同类型的图。

设G = {V, E, A}是一个有n个节点的属性网络，其中V = {v1, v2，…， v N}是节点的集合，E⊆v × v是边的集合。如果节点vi和vj之间的边eij = 1，则eije和eij = 0。A是所有N个节点的属性集合，其中aij表示节点vi的第j个属性值，如果nodev i有第j个属性，则aij的值为1，否则aij = 0。例如，在网页网络中，节点和有向边分别对应网页和网页之间的超链接，而属性可以是单词、标题、标签、主题等。

---

首先，从图G中得到由节点之间的链接确定的结构图G s = {V s, E s}，忽略属性信息;该图用于捕获网络结构中的高阶结构关系

其次，将共属性图构造为保持节点属性间共现关系的上下文图;共属性图表示为G a = {V a, E a}，其中V a 1/4 V a1;v a2;…;v a M是属性的集合，属性的每个成员都指向一个上下文节点，E a是边的集合，表示属性之间的共现关系

如果属性i和j在N个节点中同时被观察到，则节点v i和节点v a j之间的边权ea ij等于toN，否则为ea ij 1/4 0。较高的共现频率表明该属性对具有较强的相关性，这进一步意味着这两个属性之间存在较强的上下文关系。最后，在GAT2VEC方法的启发下，构造了一个二部图。二部图由两个不相交的集合组成:节点和属性。该图充当了原图与共属性图之间的桥梁。二部图表示为Gσ = {Vσ， a σ， Eσ}，其中Vσ⊆V表示在G中具有属性的结构节点的子集，Aσ表示节点关联的属性集(上下文节点)，Eσ是基于映射函数σ将结构节点与上下文节点连接起来的边集。如果G中的vi具有第j个属性，则该函数将结构节点vσi连接到上下文节点vσj。

利用上述术语，将该问题定义为一种无监督表示学习，联合学习属性网络的结构和属性上下文，生成一个低维嵌入矩阵φ∈R(N +M) × D，其中每个输入都用D维向量表示。嵌入矩阵由节点嵌入χ和内容嵌入θ组成。

4 Proposed work

提出的ANEA框架由图构建、随机游走和表示学习三个阶段组成。在图的构造阶段，如第3节所述，得到三个不同的有向图。图1给出了这些图表的说明。第一个图是由六个节点组成的结构图。有7条边表示节点之间的关系。二部图既包含结构节点，也包含上下文节点。每个结构节点都与其自己的属性相连接。例如，节点1和节点2为结构节点。它们具有与a和b相同的两个属性，因此，这两个节点都与二部图中的上下文节点a和b相连。由于这些上下文节点在多个结构节点中一起观察，在共属性图中，这些上下文节点之间创建了链接。为共属性图中的每个属性对计算归一化共现频率，并将该值赋给对的边作为边权值。得到两个属性v ai和v a j之间的边权:

其中δ是一个函数，如果两个属性都是LTH节点的属性则返回1，否则返回0。例如，考虑到图中的6个节点，上下文节点a和节点b之间的链接的边权计算为0.33，因为它们是在两个节点中一起观察到的。

在图构建阶段之后，该方法在构建的图上执行短的随机漫步，以建模节点和属性接近性。一阶接近度是指由边相连的节点之间的局部成对接近度，而二阶接近度是由节点的共同近邻数决定的。然而，随机游走使我们能够探索高阶接近性，它在节点之间投射出更复杂的关系，如路径和频繁子结构。它可以被建模为k阶马尔可夫链，其中状态空间是节点V的集合，未来的状态取决于最后k步[20,29]。随机漫步从vi开始，以有限的步数走到vj。在第th步中，随机选择一个与vi链接的节点用于第th + 1步。从而得到一系列节点序列，用来测量图中节点之间的距离。形式上，对于每个节点，从图G中提取S个长度为L的随机行走r∈r，其中r表示从各个节点开始的随机路径，r是由所有随机行走组成的语料库。例如，图1结构图中的随机游走可以是:r =(5,4,6,4)，长度为4，从节点5开始。我们在结构图上进行一系列随机游走，以获取原始网络中节点的局部和全局位置。同样，从二部图中得到一系列随机游走，提取节点与属性之间的关系。

与结构图和二部图不同，共属性图是一种加权图。因此，在共属性图上执行加权版随机漫步法。在加权随机游走中，考虑边缘概率选择与当前节点相连的上下文节点。边的概率与与该边相关的边权成正比。从v a i移动到与v a i相连的节点之一v a j的概率计算如下

其中n表示连接到节点v I的上下文节点数。加权随机游走方法对包含高权重边的路径比包含低权重边的路径有更大的偏好。因此，通过揭示在得到的属性序列中经常同时出现的属性对，可以获得更高阶的属性接近性。两个属性之间较高的属性接近性意味着这两个属性可能在语义上相关。

ANEA从结构上下文和属性上下文中获取序列后，应用SkipGram模型联合学习一个包含节点嵌入χ和内容嵌入θ的嵌入φ。anea模型的算法细节在算法1中描述。SkipGram是一种语言模型，它的目标是利用上下文窗口最大化句子中出现的词对的共现概率。为了在所提出的图结构上使用SkipGram模型，每个节点序列被评估为一个句子，并作为SkipGram的输入。在ANEA模型中，输入可以是结构节点或上下文节点。每个输入节点由一个单热编码向量表示，该向量是长度为Vs pVa的二进制向量。SkipGram使用目标节点作为输入并输出窗口中上下文节点的2w多项分布，其中w为上下文窗口大小。换句话说，目标节点用于预测目标节点左右的周围节点(上下文节点)。例如，当w等于2时，lis位置上的目标节点用于预测上下文位置(l−2)、(l−1)、(l + 1)和(l + 2)上的节点。此外，上下文节点可以是结构节点或上下文节点。

更正式地说，给定一个随机漫步r s 1/4 v s1;→;v sjr s jn o∈Rs由结构图得到，SkipGram使节点间的以下概率最大化:

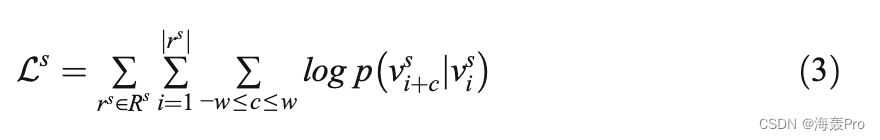
其中w调整由I估计的邻居数量。条件概率p v s þcjv s i计算如下:

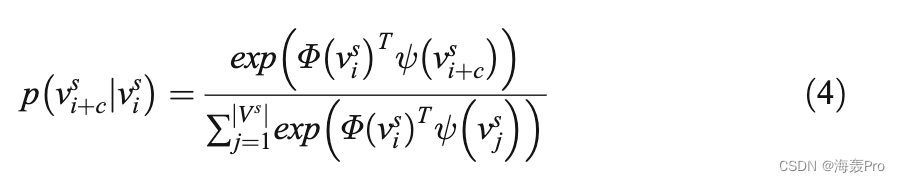
其中Φ是用于预测其周围节点的输入节点的向量，ψ是要预测的训练节点的输出向量。最初将随机值分配给两个向量，并在训练过程中学习这些值。和DEEPWALK方法一样，

由于计算概率是一项计算量大的任务，因此采用分层软最大函数来计算概率。对于分层软最大函数，采用霍夫曼编码方法将每个节点分配到二叉树的一个叶子上。到叶节点v s j的路径由一系列树节点(t0;t1;…;t logjV s jb c Þ，其中t0是根节点，t logjV s jb c是节点v s j。因此，该函数的目标是通过只遵循从根到叶节点的路径来最大化层次结构中特定路径的概率。给定一个输入节点v s i，叶节点v s j的概率定义如下:

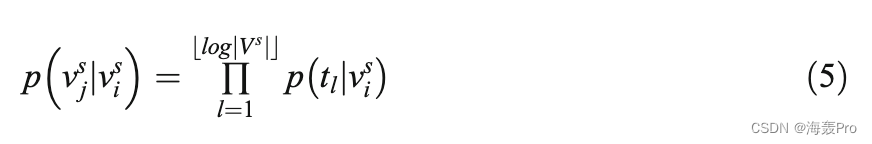
这样，计算结构节点的软最大值的问题就转化为计算树中节点从根节点到叶节点的概率乘积。这降低了计算概率p v s jjv si从O(Vs)到O(log| Vs|)的计算复杂度，因为霍夫曼二叉树的深度为log∣Vs∣。

考虑从二部图和共属性图中获得的序列，ANEA最终寻求最大化概率，如等式6中节点和属性之间的概率，以及等式7中属性之间的概率。ANEA的对数似然函数计算如下:

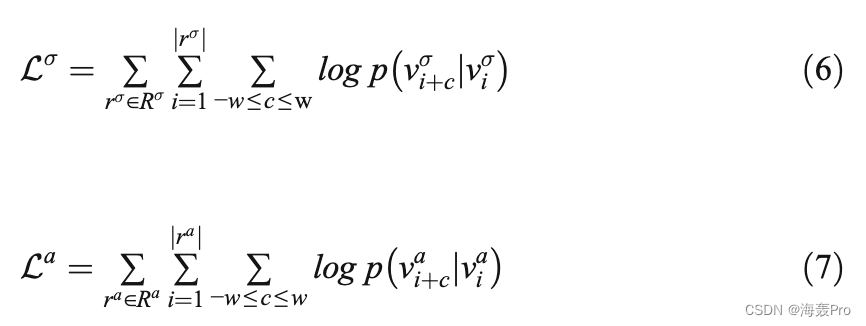
其中Rσ和Ra分别为由二部图和由共属性图得到的随机游走。同样，条件概率p vσ到wjvσi和p v到wjv a i的计算方法如式4所示。因此，计算属于三个不同图的节点的概率的复杂性导致O(log| Vs| +log| Vσ| +log|Va|)。最终，ANEA的目标是优化公式8中给出的对数似然函数L，该函数是从结构和属性上下文中获得的条件概率的和。

ANEA的架构如图2所示

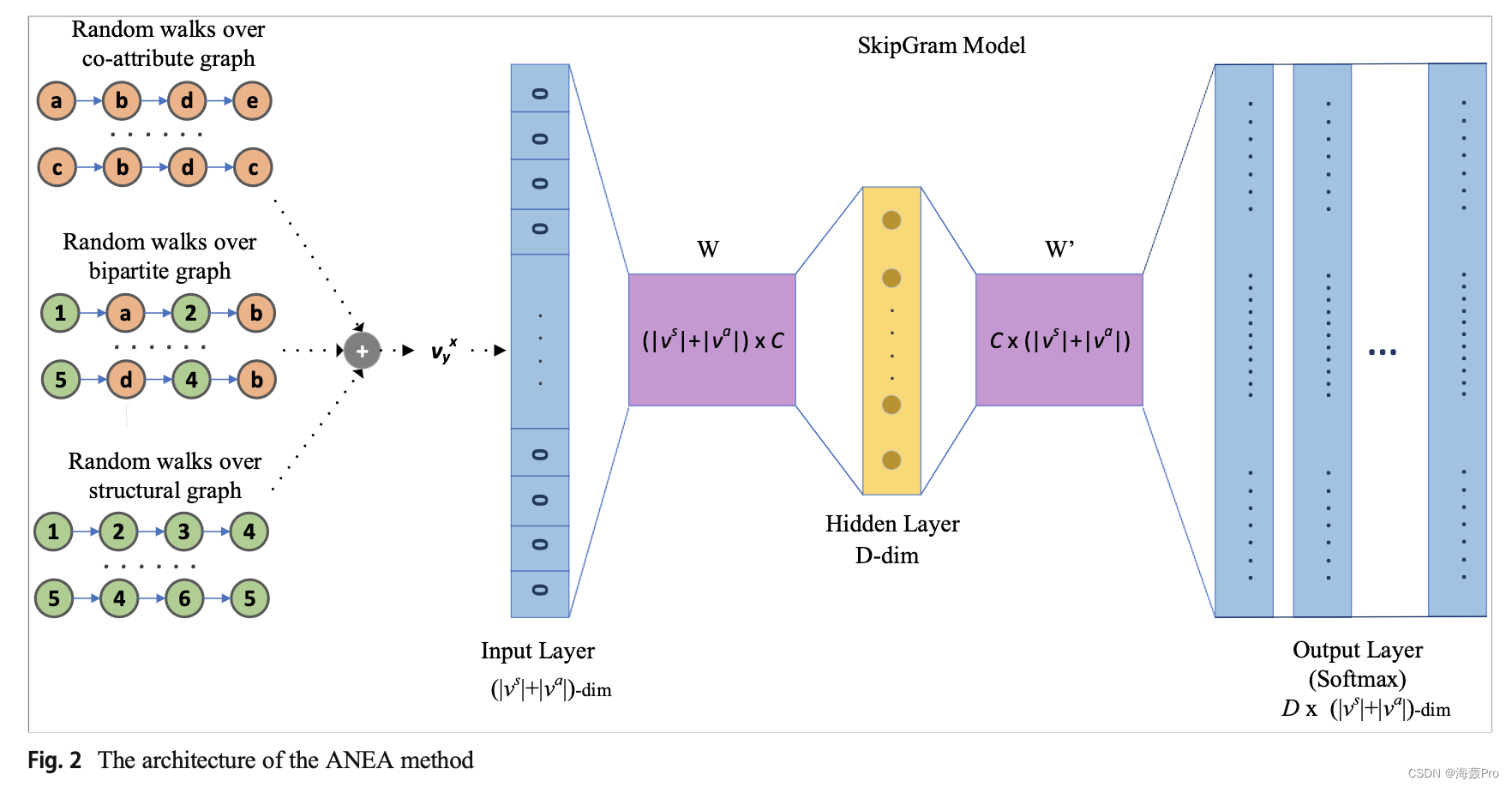
ANEA执行单层神经网络，输入作为单热编码目标节点，预期输出作为单热编码上下文节点。目标节点v x y被计算为中心节点。该模型通过预测中心节点周围的节点来训练。首先，将输入层上中心节点v x y的单热编码向量与第一权重矩阵W相乘，生成隐层矩阵;这个权重矩阵表示嵌入矩阵φ，其中每一行表示结构或上下文节点的向量。然后用相同的隐层矩阵W '乘得到各输出的多项分布，并应用softmax函数得到各节点的概率表示。在训练过程中，对给定的中心节点增加预测上下文节点的概率分布，学习长度为D的结构χ和上下文θ嵌入向量。

ANEA模型的整体计算复杂度取决于随机游走和skiipgram模型的复杂度。从图中获得短随机游动的复杂度最多为O(| V| ×L × S)。ANEA模型在三种不同的图结构上执行随机游动。因此，获得所有随机行走的总体复杂度为o ((| V s| + | Vσ| + | V a|) × L × s)。SkipGram模型的训练复杂度与w × (D + D × log| V|)[17]成正比。因此，ANEA的训练阶段复杂度为O(w × (D + D × (log| V s| +log| Vσ| +log| V a|))，因为ANEA是基于三个定义的图来计算概率的。

5 Experimental results

在本节中，通过比较提出的方法和最新的方法，报道了实验结果。在这个实验中使用了五个真实的数据集。我们对这些方法的节点分类性能进行了评价。对所提方法的参数进行了分析。此外，一些查询任务在学习到的表示上进行测试，以提供定性分析。最后，给出了节点的二维表示形式，以便更清楚地说明所提方法与其他方法的区别。

6 Datasets

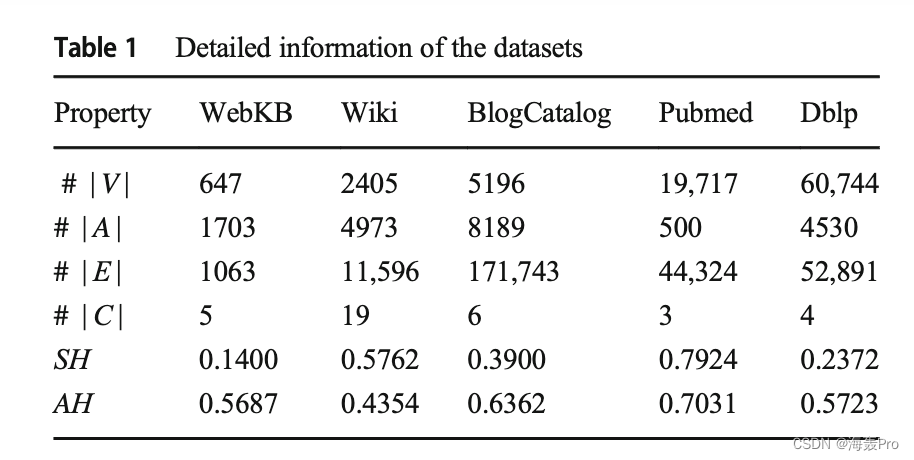
实验在从社交网络到引用网络的不同领域的公开可用的5个数据集上进行。表1总结了数据集的统计信息。Pubmed和Dblp是广泛使用的引文网络，其中每个节点对应一份科学出版物[8,21,23,30]。在引文网络中，如果一个出版物引用了另一个出版物，那么两个出版物之间就存在直接联系。每个节点都与内容信息相关联，内容信息与发布的标题相对应。WebKB和Wiki数据集由每个节点组成的网页网络组成指一个网页，每条边表示两个网页之间的超链接[22,27]。BlogCatalog是一个从在线博客社区[10]收集的社交网络数据集。如果一个博主关注另一个博主，那么两个博主之间就存在链接。博主使用的标签被认为是文本信息。表1给出了所有数据集的平均结构SH值和属性同质性AH值来解释方法的结果。网络中一个节点的结构同质性程度由其拥有与该节点相同标签的相邻节点的数量决定[4,12]。属性同质性可以通过公共属性来证明。这种同质性用来分析具有共同属性的节点是否属于同一个类。为计算属性同质度，仅考虑属性数据，构造k-最近邻图，其中ek = 5。然后，通过应用计算结构同质性时使用的相同思想，我们计算每个数据集的属性同质度。

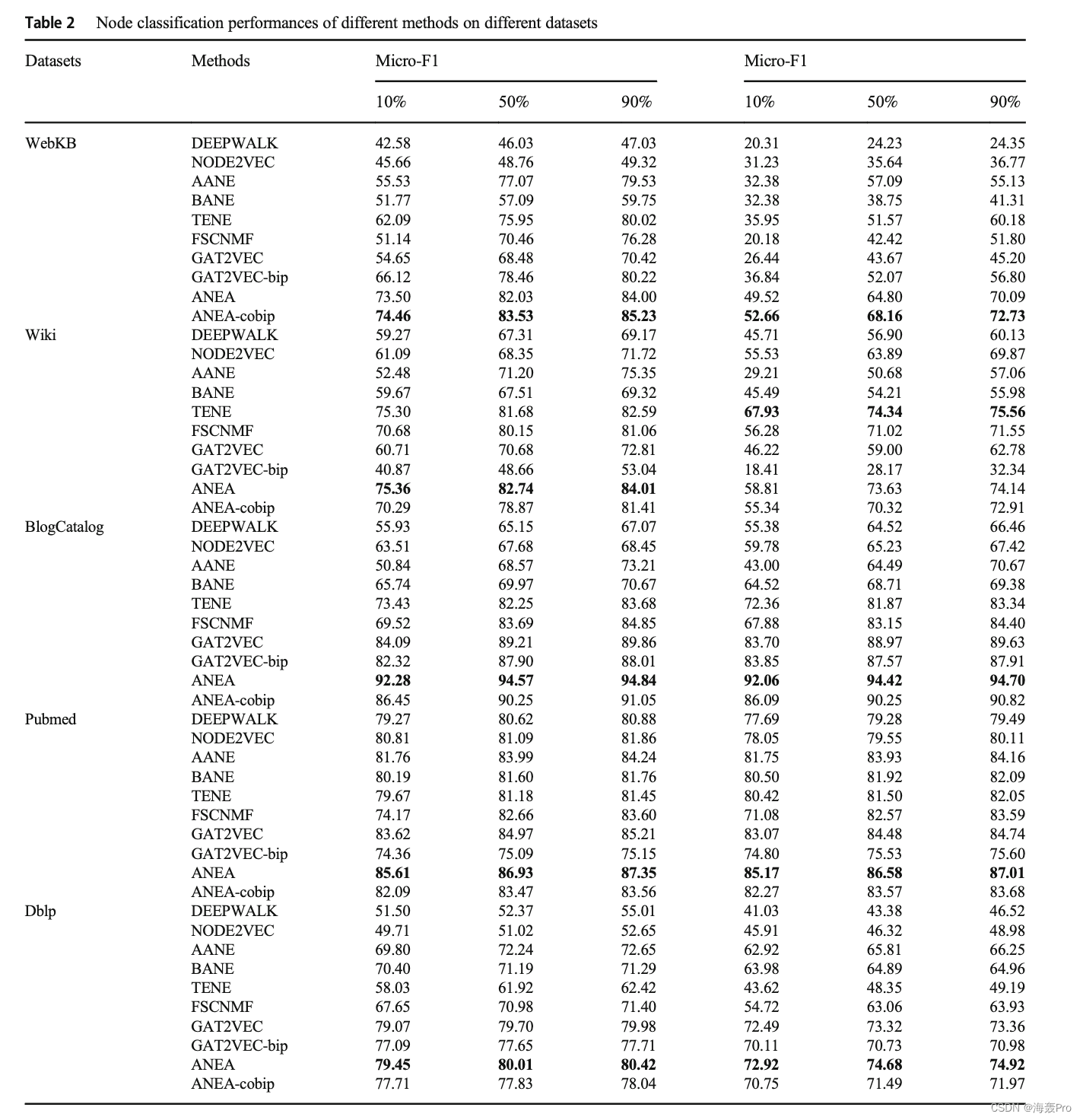
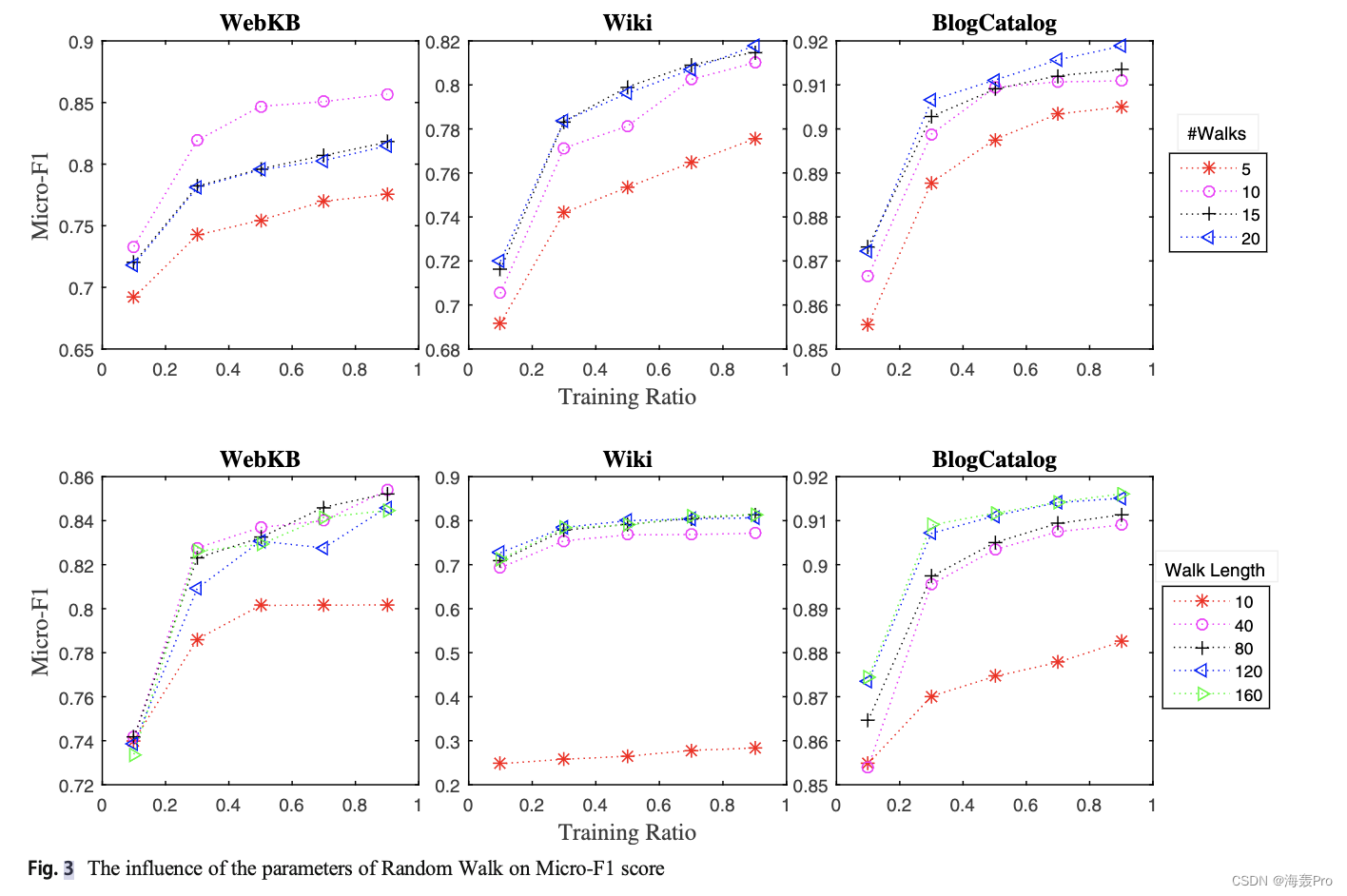
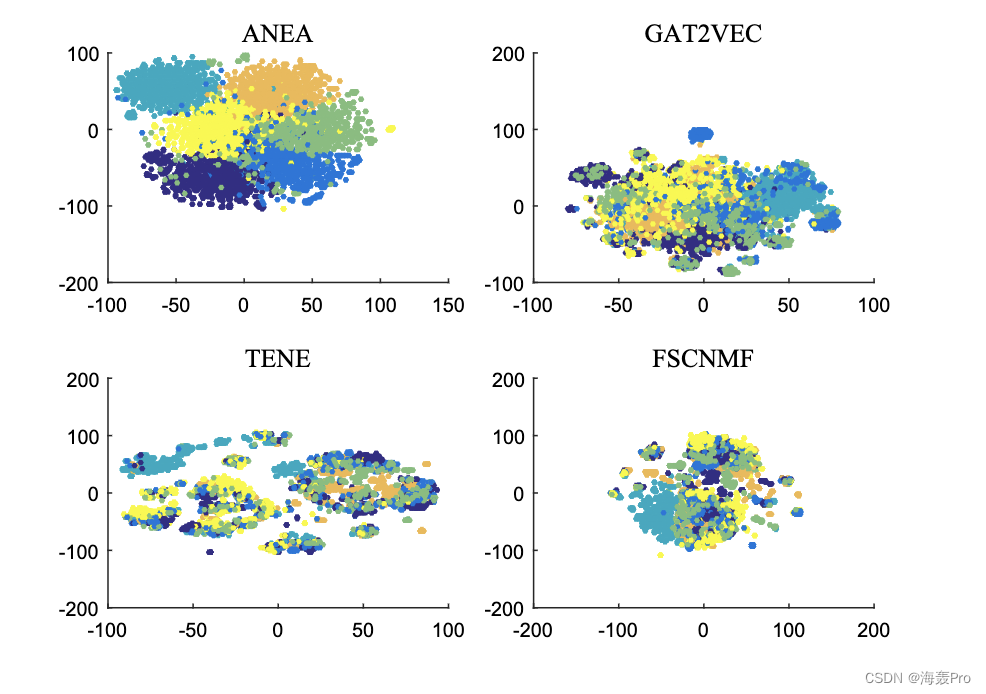
在本文中，我们提出了一个属性网络嵌入框架(ANEA)，该框架将丰富的上下文维集成到基于随机游走的图嵌入过程中，以提高学习到的节点表示的质量。我们的方法旨在保持属性之间的高阶邻域，以便更有效地建模节点之间的属性近性。因此，我们将属性数据转换为上下文图。ANEA学习由网络结构和节点属性组成的联合嵌入空间。因此，提出的方法允许生成网络中所有节点的结构和上下文表示。结果表明，与其他方法相比，我们的方法获得了明显更好的节点表示。

在未来，我们建议研究以下可能的方向。首先，随机游走过程可以倾向于网络中许多节点共享的流行属性。其次，当密切观察属性对之间的共现关系(与稀疏性问题相反)时，上下文图就变成了一个几乎完全连通的图，这导致随机游走过程不能很好地捕获局部亲缘关系。第三，在学习过程中加入上下文维度相对增加了算法的运行时间。为了解决这些问题，ANEA模型将应用一些节点和边缘采样技术进行增强。另一个可能的方向是增强动态属性网络的ANEA模型，以分析网络的演化并捕获时间变化。

结语

文章仅作为个人学习笔记记录，记录从0到1的一个过程

希望对您有一点点帮助，如有错误欢迎小伙伴指正