@TOC

前置知识

1.1随机梯度下降与梯度下降

1.2梯度下降法与最小二乘法的差异

1.3为什么需要梯度下降法

1.4梯度方向为什么是函数下降最快的反方向

1.5 指数加权平均

假设有10个数， $x_i$ :=0 1 2 3 4 5 6 7 8 9 ，想求这组数据的平均值，我们所知的方法一般是算是平均法：$$\overline{x}=\dfrac{0+1+2+3+4+5+6+7+8+9}{10}$$
还有一种方法是指数加权平均法，定义一个超参数 $\beta$（大部分情况 $\beta=0.9$）:

$$\begin{aligned}x_{0}=0\\ x_{1}=x_{0}\cdot \beta +x_{1}\cdot \left( 1-\beta \right) \\ x_{2}=x_1\cdot \beta +x_{2}\cdot \left( 1-\beta \right) \\ \vdots \\ x_{10}=x_9\cdot \beta +x_{10}\left( 1-\beta \right) \end{aligned}$$

这种方法是好处是可以节约空间，算数平均法需要保留所有值才可以求平均，而指数加权平均只需要保留当前的平均值与当前时刻的值即可，在深度学习含量数据的背景下，可以节约内存并加速运算。

理论讲解

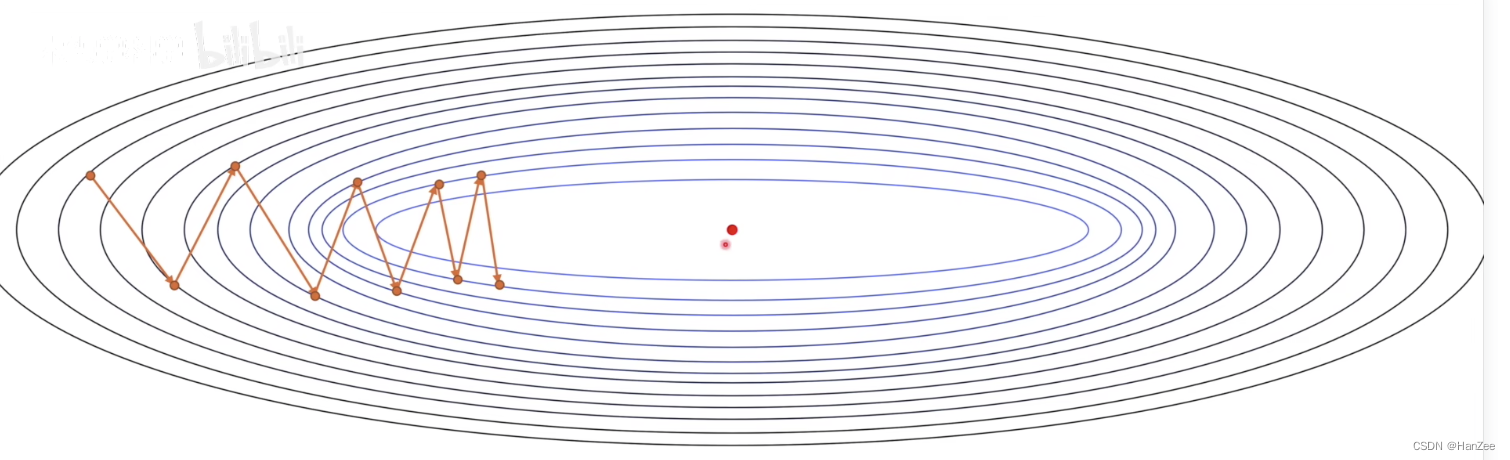
我们在使用随机梯度下降法（SGD）时，由于噪声与步长不能精准把控的情况存在，下降的过程实在震荡中实现的，如上图。我们想优化SGD考虑从下降路径上做文章。我们知道梯度是向量，导数与偏导数是标量，而每一次下降的方向都是沿着梯度方向进行的，于是我们把下降的方向分解成水平方向与竖直方向，如下图：

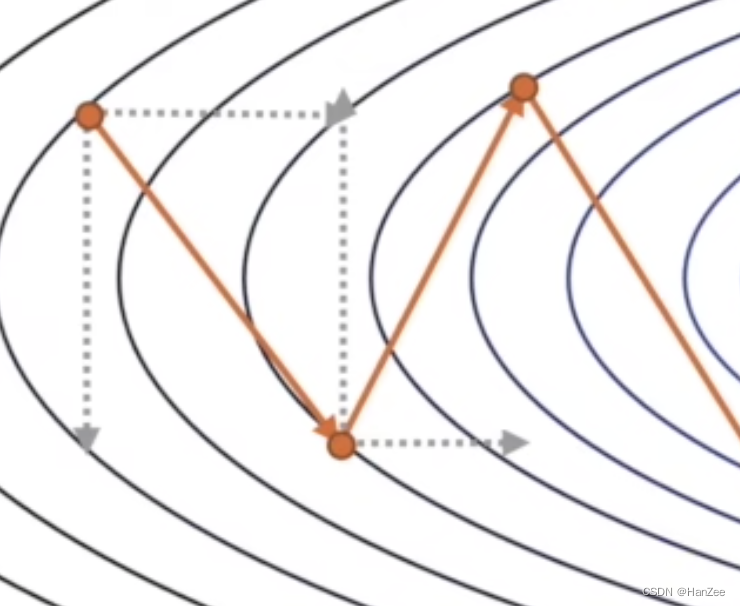
现在，我们就又了优化的方向了，如果把竖直方向削弱，水平方向增强，我们的优化速度会事半功倍。如下图：

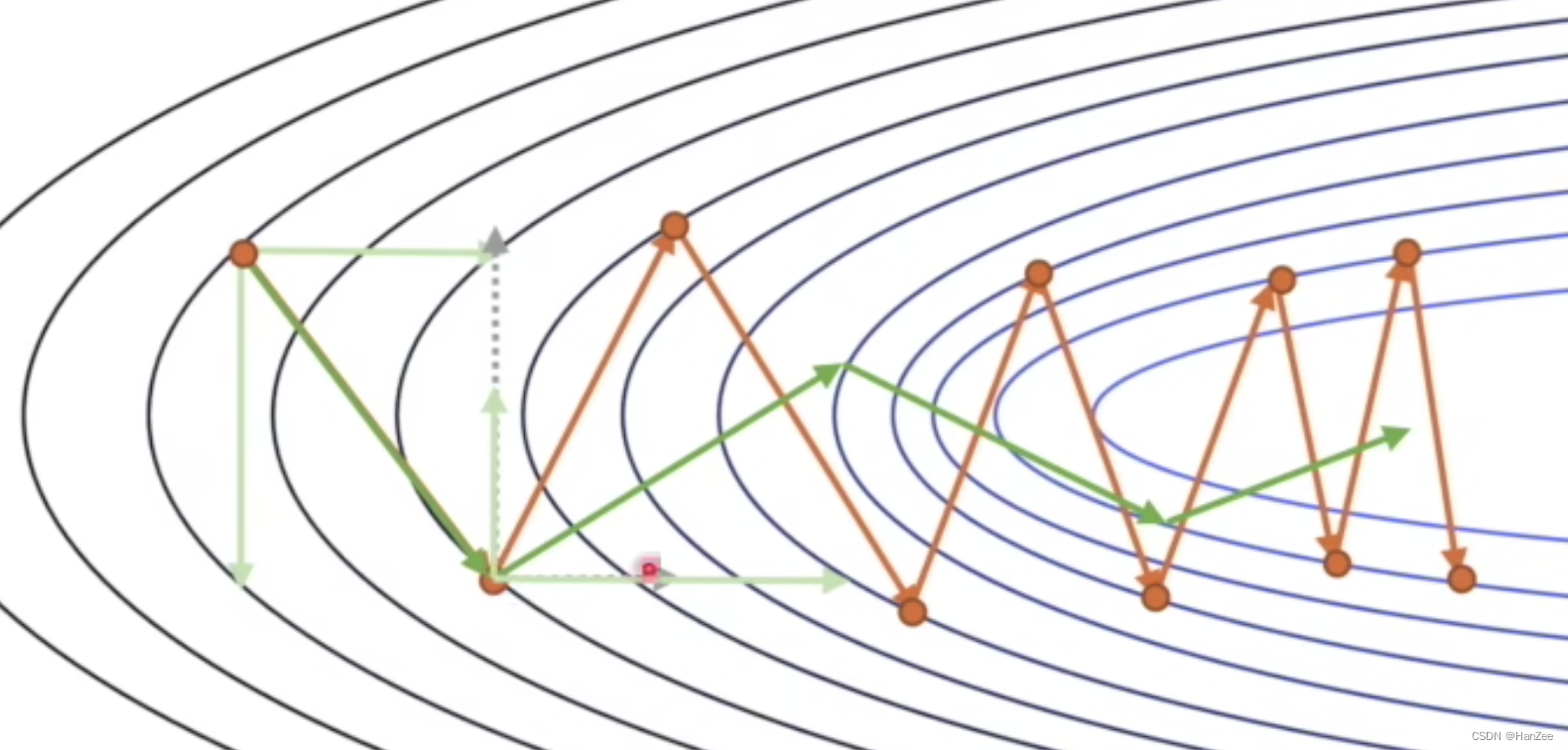
SGD的原本的公式是：

$$\begin{aligned}w_{2}=w_{1}-\alpha \dfrac{\partial loss}{\partial w_{1}}\\ b_{2}=b_1-\alpha \dfrac{\partial loss}{\partial w_{1}}\end{aligned}$$

其中偏导数代表了这个维度上移动的方向，学习率代表步长，我们把偏导数在每次优化参数时替换成加权平均的偏导数，这样考虑可以考虑前面的方向，因为当前方向前面的竖直方向是相反的，水平方向是相同的，于是就可以让函数值下降的震荡减小，速度加快。公式如下：

$$\dfrac{\partial loss}{\partial W_{2}}=\dfrac{\partial loss}{\partial W_{1}}.\beta +\dfrac{\partial Loss}{\partial W2}\left( 1-\beta \right)$$

代码实现

import torch
from torch import optim
optimizer = optim.SGD(model.parameters(), lr = 0.01, momentum=0.9)