@TOC

简介

Hello！
非常感谢您阅读海轰的文章，倘若文中有错误的地方，欢迎您指出～
 
ଘ(੭ˊᵕˋ)੭
昵称：海轰
标签：程序猿｜C++选手｜学生
简介：因C语言结识编程，随后转入计算机专业，获得过国家奖学金，有幸在竞赛中拿过一些国奖、省奖…已保研
学习经验：扎实基础 + 多做笔记 + 多敲代码 + 多思考 + 学好英语！
 
唯有努力💪
 
【每日一读】每天浅读一篇论文，了解专业前沿知识，培养阅读习惯（阅读记录 仅供参考）

论文简介

原文链接：https://www.sciencedirect.com/science/article/pii/S0925231221015125

期刊：Neurocomputing （CCF C类）

年度：2022年1月11日（发表日期）

abstract

网络嵌入的目的是学习网络中每个节点的低维向量，它在网络重构、社区检测等多种应用中都是有效的

然而,大多数现有的网络嵌入方法仅仅利用网络结构而忽视富人节点属性,这往往会产生最优的网络表示

为了了解更多理想的网络表示，需要利用网络的多种信息，在本文中，我们开发了一个新的深度自编码器框架，融合拓扑结构和节点属性称为FSADA

• 我们首先设计了一个由多个非线性函数组成的多层自编码器来捕获和保存高度非线性的网络结构和节点属性信息
• 特别是对原始信息进行预处理，可以更好地提取拓扑结构与节点属性之间的内在相关性
• 此外，我们设计了一个结合拓扑和节点属性相似度的增强模块，在节点上构造成对约束，然后在框架中引入图正则化来增强潜在空间中的表示

我们广泛的实验评估验证了该方法的优越性能。

1. Introduction

在现实中,许多复杂系统以网络的形式,如社交网络[1],学术引用网络[2],[3]和生物网络。随着网络数据的快速增长，如何处理这些大规模的网络数据带来了许多挑战。近年来，网络嵌入引起了许多研究兴趣，其目的是学习每个节点的低维向量，提取网络的内在特征。然后，学习到的嵌入表示为各种网络任务铺平了道路，如节点分类[4][5]，社区检测[6]，节点聚类[7][8]和链路预测[9]。因此，网络表示学习在网络分析中起着至关重要的作用，对网络进行适当的、信息量大的嵌入可以得到对网络的有效分析。

对于网络嵌入，已经提出了一些方法(如DeepWalk [10]， LINE [11]， node2vec[12])，这些方法主要关注于保留简单的结构信息来学习网络嵌入。然而，现实中的网络总是稀疏的，可观察到的链接的数量是有限的，因此仅仅利用结构信息可能导致次优表示。除了网络结构之外，我们日常生活中的大多数信息网络在每个节点内都有丰富的属性信息，比如引文网络中的学术话题，或者社交网络中用户的教育背景。根据社会学的同质性原则[13]等理论，拓扑结构和属性是高度相关的，该理论认为节点属性与网络结构高度相关。例如，在学术网络中，论文选题与论文被引量之间存在高度的相关性，它们相互影响、相互决定。论文[14][15]验证了同时利用结构和节点属性可以获得更好的嵌入性能。因此，利用节点属性可以学习比单独使用网络结构信息更有信息量的网络嵌入。此外，加入更多类型的信息可以过滤掉噪声信息，准确地刻画网络，最终得到理想的网络表示。

---

虽然已经提出了许多网络嵌入方法并取得了合理的效果，但我们仍然面临着三大挑战:

• 第一，现有的方法将拓扑结构和节点属性视为线性的，并且假设它们之间的相关性也是线性的。然而，已经证明，网络和属性信息的底层结构通常最好被认为是高度非线性的[16][17]。此外，两类信息之间的内在相互作用也是高度非线性的[18]
• 其次，如何有效捕获拓扑结构与节点属性信息之间的复杂关联是一个难点。以往的工作只是将单个结构和节点属性用一个浅层模型结合起来，没有充分考虑它们之间复杂的相互作用
• 第三，如何有效地整合不同类型的信息，学习所需的网络嵌入仍有待解决。整合应遵循一个基本原则，即将原网络中结构和属性接近度较大的节点紧密嵌入到潜在空间中。如前所述，一种有效的方法可以同时捕获和保存非线性拓扑结构和节点属性，以及它们之间的内在相关性。

---

在本文中，我们提出了一种通过深度自编码器FSADA融合拓扑结构和节点属性的嵌入框架

与现有的方法相比，FSADA在一个统一的框架内解决了上述三个主要挑战

该框架的主要新颖之处在于

• 既考虑了高度非线性的拓扑结构，又保留了重要的节点属性信息
• 此外，与以往简单地将结构信息和节点属性信息结合在一起的算法不同，我们的方法充分考虑了两类信息之间的复杂交互作用，并利用预处理过程捕捉到它们之间深刻而复杂的关系
• 此外，我们还设计了一种增强方案来提高网络嵌入的有效性和效率。

在此基础上，我们设计了一种深度自编码器，该编码器具有多层非线性函数，以同时保留非线性拓扑结构和节点属性

我们根据结构二阶接近度和节点属性接近度定义损失函数，然后通过最小化最终损失函数来实现嵌入

特别是，虽然网络结构和节点属性是网络的多视图，但它们来自不同的来源

因此，我们采用预处理程序对这两类信息进行预处理，得到密度大且无冗余的高阶特征

然后，将高阶特征水平拼接为自编码器的输入，有助于挖掘结构与节点属性信息之间的复杂相关性

此外，为了进一步提高性能，获得更有效和高效的网络嵌入，我们设计了一个增强模块

在增强模块中，我们在节点上构造成对约束，并在目标函数中引入图正则化来加强潜在嵌入。

---

总结而言，我们的工作有以下几点贡献:

• 我们开发了一个由多个非线性函数组成的多层自编码器来捕获和保存高度非线性的拓扑结构和节点属性信息。
• 采用预处理程序对原始拓扑结构和节点属性进行预处理，然后将得到的高阶特征输入自编码器进行进一步学习，便于挖掘它们之间的复杂相互作用。
• 为了进一步提高嵌入的性能，我们设计了一个增强模块。该算法通过结合结构和属性相似度构造成对约束，并在框架中引入图形正则化来增强潜在空间中的节点表示。
• 我们在现实网络中进行了大量的网络重构和节点分类任务实验，以评估模型的有效性。实验结果表明，该模型能够学习到信息量大、质量高的嵌入信息，并在两项网络分析任务中显著优于现有方法。

2. Related work

2.1. Structure preserving network embedding

近年来，网络嵌入受到了广泛关注，各种网络嵌入方法层出不穷

例如

• DeepWalk[10]是先锋的网络嵌入方法，它利用跳克模型和短随机行走流来学习节点表示
• node2vec[12]是DeepWalk的扩展，结合了这两种搜索风格来探索和捕获网络中的高阶邻近性
• M-NMF[19]将群落结构和微观结构结合到网络嵌入中
• NECS[20]与M-NMF思想一致，保留了高阶邻近性，并在网络嵌入中融入了社区结构
• 提出GNE[21]作为一种球形嵌入方法来维护分层社区结构，学习节点表示
• HNS[22]是一种新的负采样方法，利用建模邻居信息进行负采样。此外，该模型利用分层狄利克雷过程(Hierarchical Dirichlet process)来探索网络潜在的社区结构。

然而，上述方法都是浅层模型，不能有效地捕捉高度非线性的信息

此外，由于深度学习具有强大的表示能力，采用多种深度方法对网络嵌入进行学习

例如

• 提出了SDNE[23]作为半监督深度模型，利用二阶接近度作为无监督部分，一阶接近度作为有监督部分，分别捕获全局和局部网络结构
• DNGR[24]采用堆叠降噪自编码器，采用卷积神经网络学习节点嵌入
• 提出了一种基于对抗性自编码器的正则化表示学习网络嵌入方法ANE[25]
• Tu[26]提出了一种新的深度超网络嵌入模型，该模型采用一种深度模型来保持局部和全局的近性
• DSINE[27]是一个深度结构影响学习模型，它融合了来自对齐自网络的信息，以保持局部和全局结构
• TEA[28]是一种基于深度自编码器的三损耗增强网络嵌入方法，既保留了网络结构又保留了节点判别信息。

2.2. Attributed network embedding

上述方法均仅利用网络结构信息获取网络嵌入，忽略了重要节点属性，导致性能不理想

最近，在利用有用的节点属性生成嵌入方面做出了一些努力

• 在第一次尝试中，TADW[29]被提出为一种矩阵分解方法，利用与网络中节点相关的文本特征来获得嵌入
• 提出了深度属性网络嵌入方法DANE[30]，同时保持语义邻近性、高阶邻近性和一阶邻近性。此外，该模型保证了学习到的表示与结构和节点属性一致。
• AANE[31]是一种可扩展的高效框架，它将节点属性接近性与结构结合起来生成网络表示
• Jin等[32]通过深度自编码器开发了网络嵌入框架UWMNE。将模块矩阵和属性马尔可夫矩阵输入到深度自编码器中进行网络嵌入
• Yang等[15]提出了一种基于多视图关联学习的不完全网络深度嵌入方法，综合了网络的结构和性质
• ASNE[33]采用深度神经网络体系结构来捕获结构邻近性和属性邻近性
• NetVAE[34]是一个特定于网络的变分自编码器，用于嵌入网络的结构和属性信息
• ONE[35]是一种结合拓扑和节点属性，并结合异常值检测的无监督属性网络嵌入方法
• RODE[36]是一个深度嵌入模型，它通过探索结构和语义相似性来学习网络嵌入
• Liu等人[37]开发了一种可扩展的属性感知网络嵌入方法，从网络结构和属性中学习联合节点表示
• SNEQ[38]结合了通过自注意层学习的量化，该层利用了节点标签、结构接近性和节点属性。

此外，卷积神经网络作为解决各种图学习任务的有前途的工具已经引起了广泛的关注

• 图卷积网络(GCN)[39]是一种基于图卷积神经网络的半监督学习方法，用于节点分类
• 图自动编码器(Graph Autoencoder, GAE)[40]利用GCN同时编码节点结构信息和节点特征信息。GAE的编码器由两个图卷积层组成
• 在此基础上，提出了一种基于变分自编码器学习数据分布的变分GAE版本，称为VGAE。与GAE类似，GraphSAGE[41]用两个图卷积层编码节点特征。它通过学习不同深度邻居节点的聚合器来生成嵌入
• Wu等人[42]提出了一种极其简化的图卷积(SGC)体系结构，通过去除非线性和折叠连续层之间的权矩阵，减少了过多的复杂性。

3. Notations and problem definition

在整个论文中，我们使用大写字母表示矩阵，使用小写字母表示标量。矩阵A的i掷由ai和i表示;矩阵的元素Jð Þth用ij表示。我们还用Tr Að Þ表示矩阵的迹，用jjAjjF表示矩阵A的Frobenius范数。

我们假设网络是一个无向图V;E;Tð Þ，其中V表示n个节点的集合，E表示边的集合。图G的拓扑结构可以用邻接矩阵a2 Rn n表示，矩阵t2 Rn d表示n个节点的属性信息，矩阵T的第i行表示节点vi 2v的d维属性特征。

问题1(网络嵌入)。给定一个具有邻接矩阵a2 Rn n和属性矩阵t2 Rn d的网络G，我们旨在学习一种低维向量表示u2rn m，期望它能保留网络的底层结构和节点属性:

其中f ð Þ是将原始网络表示嵌入到低维表示中的变换函数，m是学习到的网络表示的维数

定义1(一阶接近)。网络中的一阶近性ys 1ð Þ 2rn n是两个节点[11]之间的局部成对近性。如果六世;vj2e, vi和vj之间有一阶接近性，否则，一阶接近性为0

定义2(二阶接近度)。二阶接近性S 2ð Þ 2 Rn n表示一对节点的邻域结构之间的相似性。N u 1/4 S 1ð Þu1;。； s1 ð Þun表示节点vu与其他节点之间的一阶接近度，vu与vw之间的二阶接近度由N u和N w的相似度决定

定义3(节点属性接近性)。对于给定的网络，节点属性矩阵记为t2 Rn d，其中d为节点属性类的个数，T的行表示对应节点的属性向量。属性的接近度由矩阵T中对应行之间的相似度表示。

除了网络结构之外，我们日常生活中的大多数信息网络在每个节点内都有丰富的属性信息，这些节点属性携带着语义信息，利用这些语义信息可以至关重要地提高网络嵌入的准确性

例如，在图1中，节点表示作者，作者发表的会议表示节点的属性

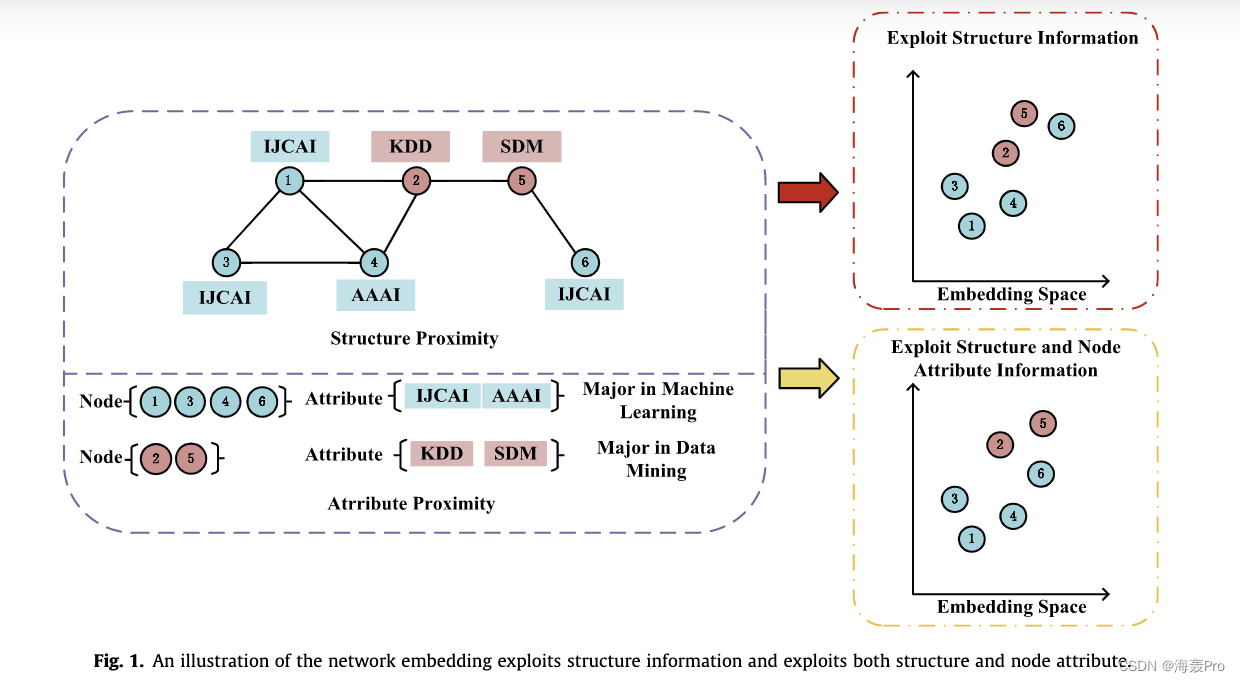
当仅利用结构信息获取网络嵌入时，通常的假设是，如果两个节点具有相似的结构，那么它们在低维嵌入空间中应该是接近的

如图1右上方所示，仅考虑网络结构，节点1;2;3;4f g和节点5;6f g在嵌入空间中应该彼此接近，红色箭头指向仅利用网络结构生成的网络嵌入

然而，在现实世界的信息网络中，观察到的链接是有限的，没有直接连接的节点并不意味着它们完全不相关

例如，虽然节点6与节点1、3、4没有直接连接，但它们具有相似的属性(相似的研究主题)，但我们也认为它们应该相似并紧密嵌入

这是因为他们都是机器学习专业的，虽然他们没有直接的联系，但他们很可能对同样的文献或学术会议感兴趣

如图1右侧所示，黄色箭头所指的是同时利用网络结构和节点属性生成的网络嵌入

与只考虑网络结构的网络嵌入相比，节点6在嵌入空间中更接近节点属性相似的节点1、3、4

因此，节点属性信息能够为拓扑结构提供重要的补充，更好地表征网络结构，同时缓解网络稀疏问题

与单纯利用网络结构的网络嵌入相比，同时利用网络结构和节点属性的网络嵌入信息量更大，更可取

节点属性对于增强网络表示学习非常有用。我们利用节点属性来学习网络表示，并期望具有相似属性的节点应该彼此紧密嵌入。

4. The framework of FSADA

4.1. Overall framework

该框架的整体架构由三个主要模块组成，如图2所示

• 在第一个模块中，我们用图的形式表示网络结构和节点属性
• 在第二个模块中，我们提出了一种带有预处理生产者的深度自编码器，以捕获和保存非线性拓扑结构、节点属性以及它们之间的复杂相关性
• 在第三个模块中，我们设计了一种增强算法，约束原网络中具有相似结构和节点属性的节点在嵌入空间中也彼此接近。

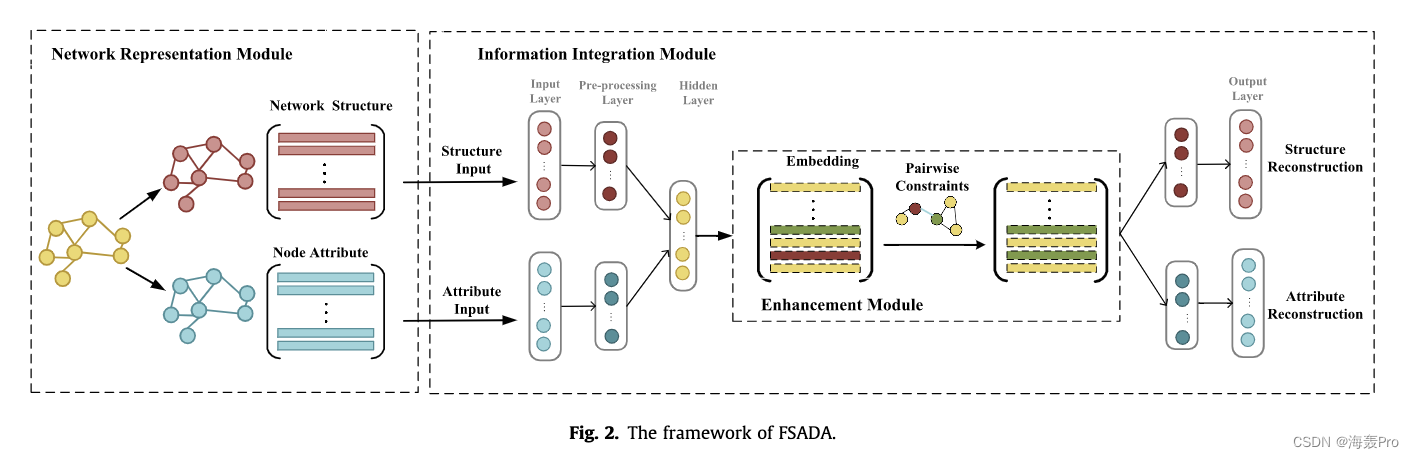
网络表示模块:我们将拓扑结构和节点属性以图的形式表示出来，并将对应的相邻矩阵和属性矩阵作为模型的输入。

信息集成模块:为了捕获高度非线性的拓扑结构和节点属性，我们采用了深度自编码器模型。该自动编码器将原始数据映射到能尽可能重构原始数据的低维嵌入中，并将隐藏层中的编码视为网络表示。我们设计了基于结构邻近性和属性邻近性的损失函数，既保留了网络结构又保留了节点属性信息。由于结构和属性信息往往是稀疏和有噪声的，我们首先对原始拓扑和节点属性分别进行预处理，得到它们的密集和非冗余的高阶特征。然后将这两个高阶特征水平连接，作为多层自动编码器的输入数据。与直接采用稀疏矩阵作为自编码器输入相比，采用预处理过程可以缓解稀疏性问题，滤除噪声信息。从而有利于提取拓扑结构与节点属性之间的内在相互作用。

增强模块:为了获得高质量的嵌入，我们对潜在的嵌入空间设计了一个增强模块。直观上，我们认为如果两个节点在原网络中具有较高的拓扑和属性接近性，那么它们应该被紧密嵌入。为此，我们构造一个融合链接和属性相似度的聚合图来衡量两个节点之间的接近度。基于接近性，我们在节点之间构造成对约束，并在模型中引入一个图正则化。增强模块增强原网络中具有相似结构和属性的节点，使其在嵌入空间中彼此接近。

4.2. Deep autoencoder for embedding

自动编码器是一种功能强大的无监督深度模型，它可以用来学习一种最接近原始数据的新表示。近年来，自动编码器在许多领域都取得了巨大的成功。自动编码器包含两个对称组件:编码器和解码器。

其中h 1/4 W 1ð Þ;W 2ð Þ;B 1ð Þ;B 2ð Þ为编码器和解码器中的参数，r ð Þ为非线性映射，如sigmoid函数r xð Þ 1/4 1 1þexp xð Þ。给定输入数据xi，编码器将原始数据xi映射为低维嵌入向量hi。习得的hi可以看作是xi的嵌入表示。然后用解码器重构输入数据xi， ^xi是解码器重构的数据。

自动编码器的目标是使重构数据与原始数据之间的差异最小化，使最后一层隐藏层能够最大程度地保留原始输入数据的特征。我们通过最小化重构误差来学习模型参数:

为了充分捕捉拓扑结构和节点属性中的高度非线性，本文的编码器和解码器由多个非线性函数组成。

相应的，k 1/4 1;2;。； K和K是层数，h K ð Þi表示第i个节点的低维表示。

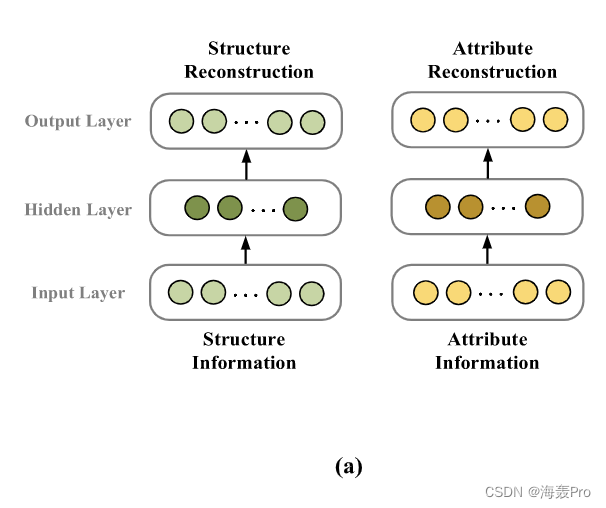
为了将网络结构A和节点属性T保持在一个统一的框架中，我们引入了三种拓扑结构和节点属性在最终表示中的融合方式，分别是分离模式、连接模式和预处理模式。

分离模式:如图3 (a)所示，将结构和属性数据结合起来，最直观的方法是采用两个自编码器模型分别学习。然后在最后一个隐层中，将表示拓扑结构的两个编码的h1 ð Þ和h2 ð Þ与节点属性值进行组合，得到最终的联合表示。该模式最大的局限性是无法探究结构与节点属性信息之间的相关性。

连接模式:另一种直接的方法是首先将这两种类型的信息作为输入连接到自动编码器。与独立模式相比，该模式能在一定程度上捕捉到两类信息之间的相关性。但是，由于网络结构和节点属性信息极其稀疏和冗余，因此该模型很难获得它们之间的交互关系。同时，当两个输入向量的长度有较大的散度时，该模式无效。

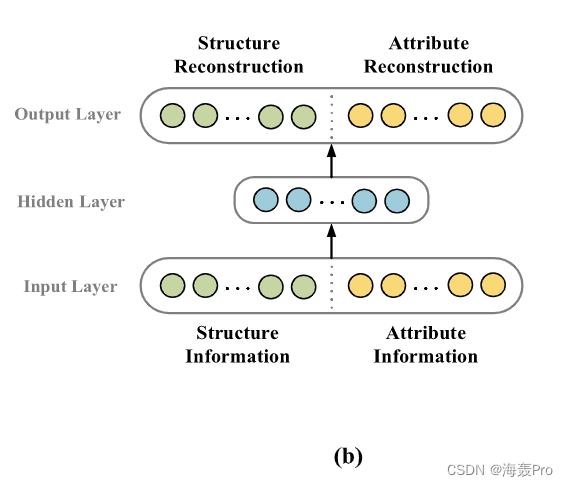
预处理模式:如图3 ©所示，为了更好地捕捉结构信息和属性信息之间的相互作用，我们引入了一种带有预处理层的自编码器学习方法。我们对每个信息使用预先训练的层，然后得到它们的密集和非冗余的高阶特征。然后，将高阶特征水平连接，前馈到模型中。与上述两种模式相比，采用预处理后的高阶特征作为自编码器输入有利于提取不同类型信息之间的内在相关性。

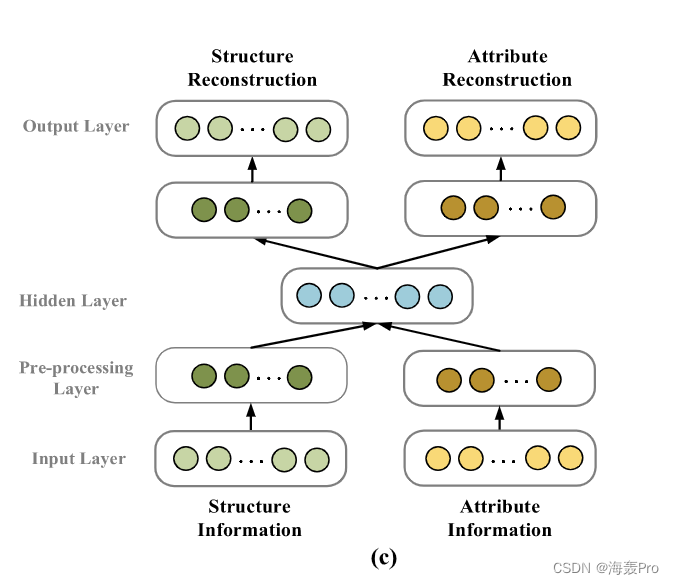
如前所述，为了更好地捕捉高度非线性的拓扑结构、节点属性信息以及它们之间的相关性，我们采用预处理模式。该模型分别对网络结构和节点属性进行预处理，可以滤除噪声和冗余信息。通过预训练算法，预处理层可以提取两类信息的高阶特征。然后，将高阶特征水平连接，作为多层自编码器的输入进行进一步学习，便于捕获它们之间的复杂相关性。值得注意的是，结构信息和节点属性信息的预处理层具有不同的权重矩阵。

4.3. Loss functions

本节在深度自编码器的基础上，介绍FSADA的损耗函数。我们首先描述了自动编码器模型如何利用二阶邻近性来保持网络结构。然后我们描述了该模型如何利用属性接近性来保留节点属性。

4.3.1. Preserving topological structure proximity

在本文中，我们利用二阶接近性来保持拓扑结构。二阶邻近性是指一对节点的邻域结构的相似性，它可以表征全局网络结构。论文[23]表明，与一阶邻近性相比，网络中具有二阶邻近性的节点较多。因此，二阶接近度能够在学习网络表示中提供进一步的信息。此外，利用二阶接近性可以缓解邻接矩阵的稀疏性问题。因此，现有的一些工作利用二阶接近度来捕捉网络结构。也有一些作品同时利用了一阶和二阶接近性。在我们的工作中，我们关注的是二阶接近度。这是可以接受的，因为在增强模块中已经在一定程度上考虑了一阶接近性。

我们通过重构邻域结构来获取二阶邻近性，确保具有相似邻域结构的节点将彼此紧密嵌入。对于网络，节点的邻域结构可以用邻接矩阵的相应行表示。因此，我们使用邻接矩阵A作为模型的输入。然而，可观察到的链接的数量是有限的，网络通常是极其稀疏的。两个节点之间没有可观察到的联系并不意味着它们不相似。此外，在邻接矩阵A中，零元素的个数远远多于非零元素的个数。为了解决这个问题，我们利用权重策略对非零元素的惩罚大于对零元素的惩罚。为了保持二阶接近性，我们将重构损失最小化如下:

其中Ba 1/4 b a i n i1/41, if a ij 1/4 0;B a ij 1/4 1，否则B a ij 1/4 g1 > 1ð Þ。这是阿达玛乘积。非零元素可以充分保存结构数据。我们将邻接向量放入多层自编码器中，具有相似邻接结构的节点将具有相似的潜在表示hi。

4.3.2. Preserving Node Attribute Proximity

除了拓扑结构外，节点属性的运用对网络嵌入有重要的改善作用。此外，加入更多类型的信息可以过滤掉噪声信息，准确地刻画网络，最终得到理想的网络表示。类似地，我们通过重构节点属性邻近性来学习节点表示，确保具有相似属性的节点将被紧密嵌入。属性接近性损失函数公式如下:

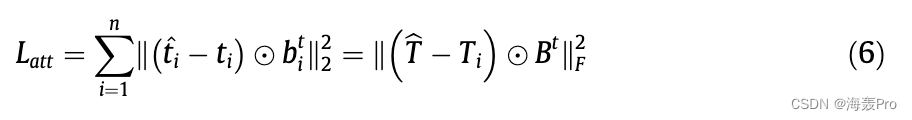
其中B t 1/4 B t in on i1/41, if t ij 1/4 0;B t ij 1/4 1，否则B a ij 1/4 g2 > 1ð Þ。该自编码器通过最小化重构损失，可以更好地捕获语义内容中隐藏的局部流形几何。因此，通过最小化重构损失，使属性向量相似的节点具有相似的低维表示，从而保持属性的接近性。为了同时保持结构接近性和属性接近性，我们将式5和式6结合得到目标函数:

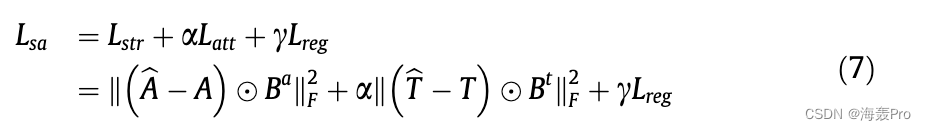
一个;C为正参数，用于平衡相应组件的贡献。Lreg是防止过拟合的正则项:

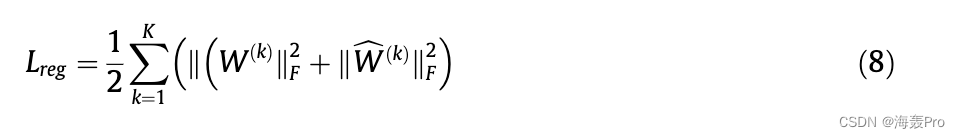
4.4. Enhancement module

为了进一步提高网络嵌入的有效性和效率，我们设计了一个增强模块，并通过在节点上构造成对约束和在目标函数中引入一种新的图正则化来实现该增强模块。受到拉普拉斯特征映射方法的启发，当高度相似的节点在潜在表示中映射得很远时，我们施加惩罚。我们首先引入两个节点之间的相似度来度量节点的接近度[43]。一般流程如图4所示。然后，我们在节点中定义成对约束以增强潜在表示。

首先，我们引入一种度量网络中两个节点之间的相似度的方法，将它们的链接强度与属性相似度融合在一起。对于每个顶点vi，计算其n个最相似内容的邻居。采用余弦相似度作为两个属性向量之间的相似度。两个内容向量的余弦相似度为:

对于vi的前n个邻居vj，一条边vi;vj被添加到内容边缘Ec。然后，我们将内容边集Ec和原始拓扑边集Et合并为边并Eu。在边缘联合Eu中，分别计算拓扑相似度和属性相似度。对于拓扑相似度，我们使用Simt 1/4 Sim ij thi1 /4 cosa i计算拓扑相似度;节点vi和它的邻居之间的Aj。对于属性相似度，我们使用Sim c 1/4 Sim ij ch i1/4 s ij计算节点vi与其邻居之间的属性相似度。在计算拓扑相似度和属性相似度后，将其归一化为0 - 1，将相似度值缩放为0;11

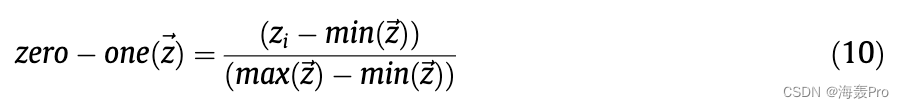
最后，我们选择Eu中最相关的边来保留一个新图G new。我们选择相似值最高的ffiffihijjp边保留，其中Hij为vi在Eu中的邻居数。

在得到图Gnew后，我们定义一个两两约束矩阵O 1/4 oij2rn n，其中如果节点vi和vj在Gnew中有边，则O ij 1/4 1;Oij 1/4 0否则。因此，我们可以将成对约束写成:

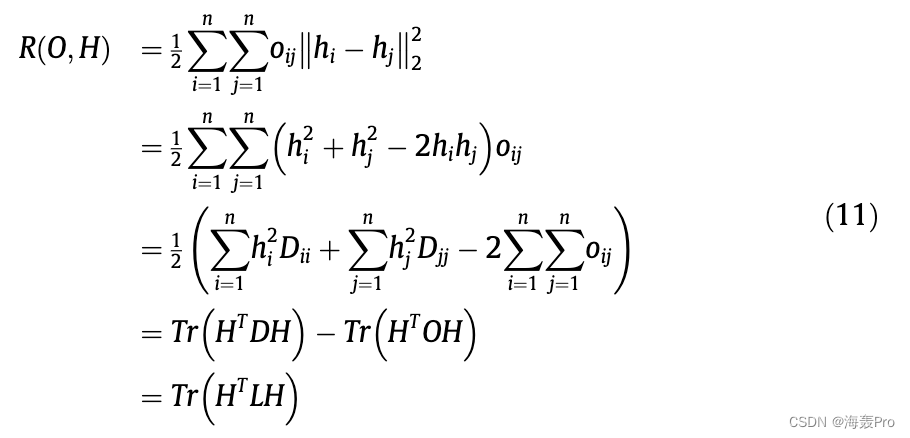
其中D是矩阵O的对角矩阵，D /4 Pn j1/41oij。拉普拉斯矩阵l1 /4 D O为图正则化矩阵，我们将式12中的函数视为图正则化项。通过最小化R O;h - ð Þ，我们惩罚结构和属性相似度高的节点在嵌入空间中会彼此远离。然后，将图正则化项合并到重构损失函数中，得到FSADA的总体损失函数为:

其中b为两个模块权重均衡的参数。

4.5. Optimization

Eq。12可以被反向传播优化随机梯度下降法。然而,由于很难获得最优结果的高非线性模型。因此，我们首先使用深度信念网络对参数进行预训练，找到合适的参数区域[44]。然后，在预训练权值的基础上进一步优化模型。算法框架总结为算法1。

5. Experiments

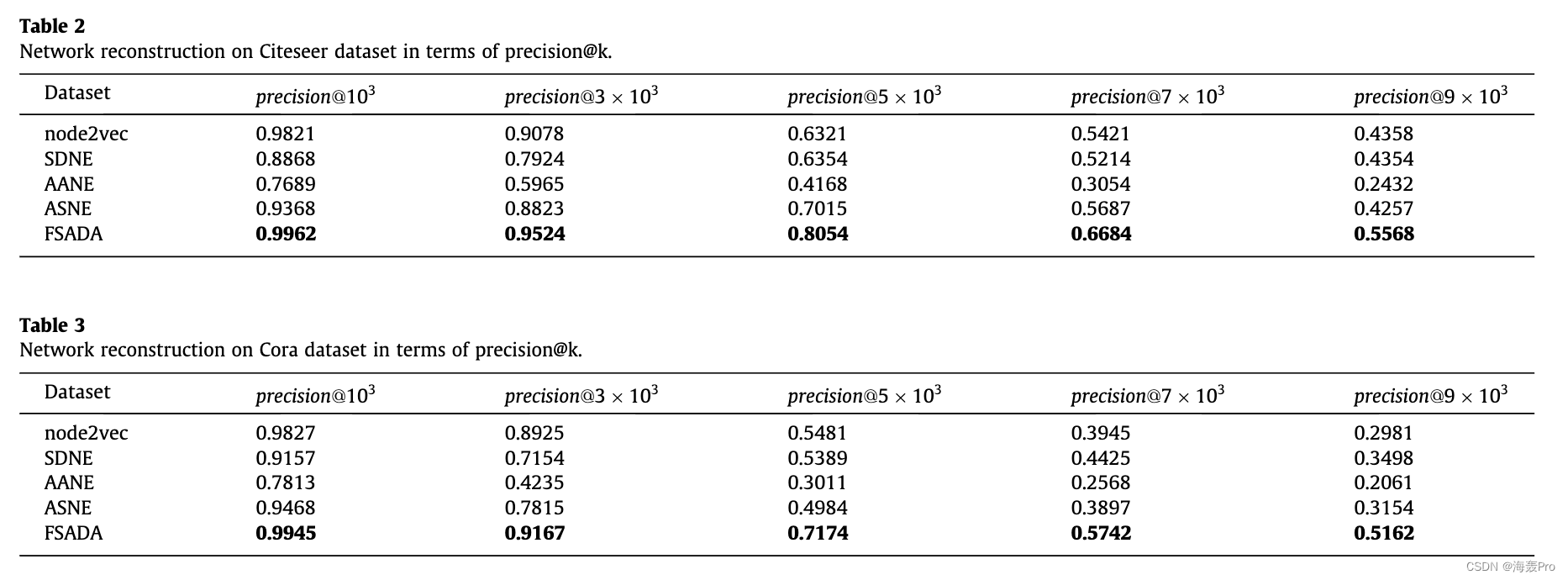
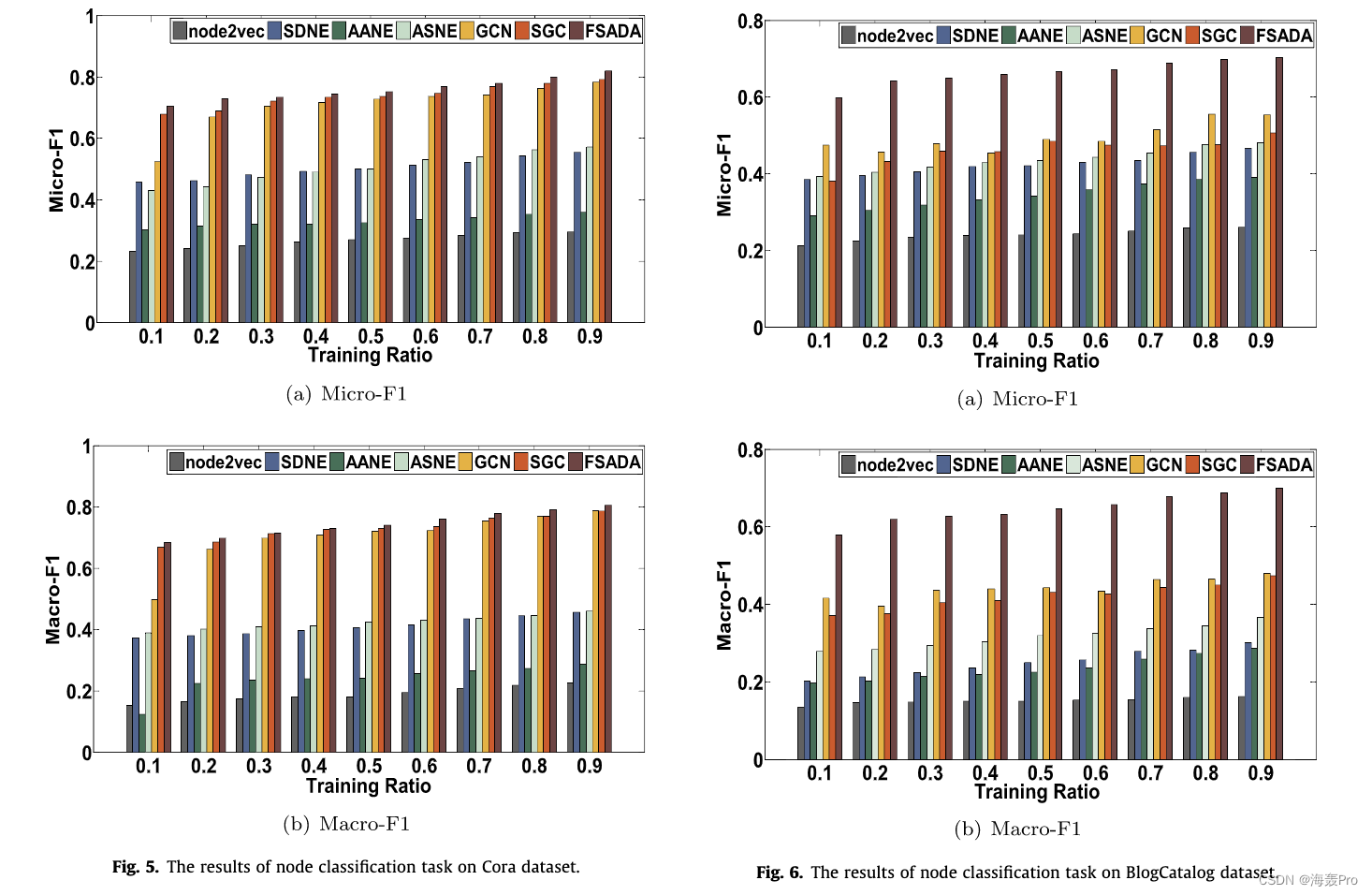
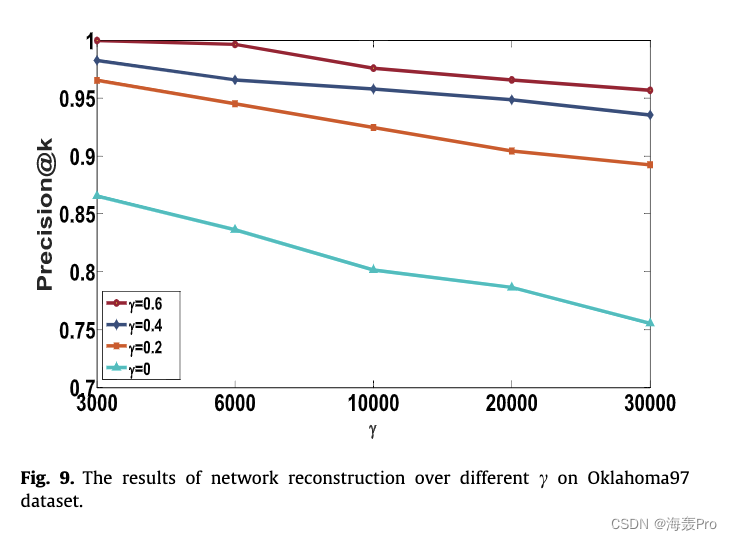
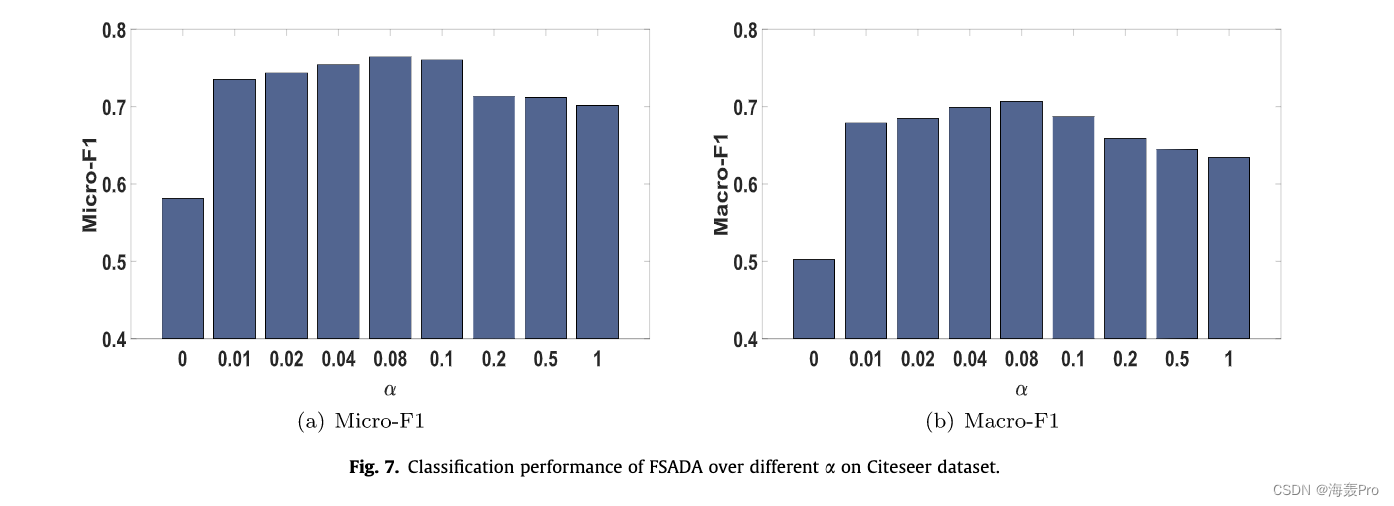
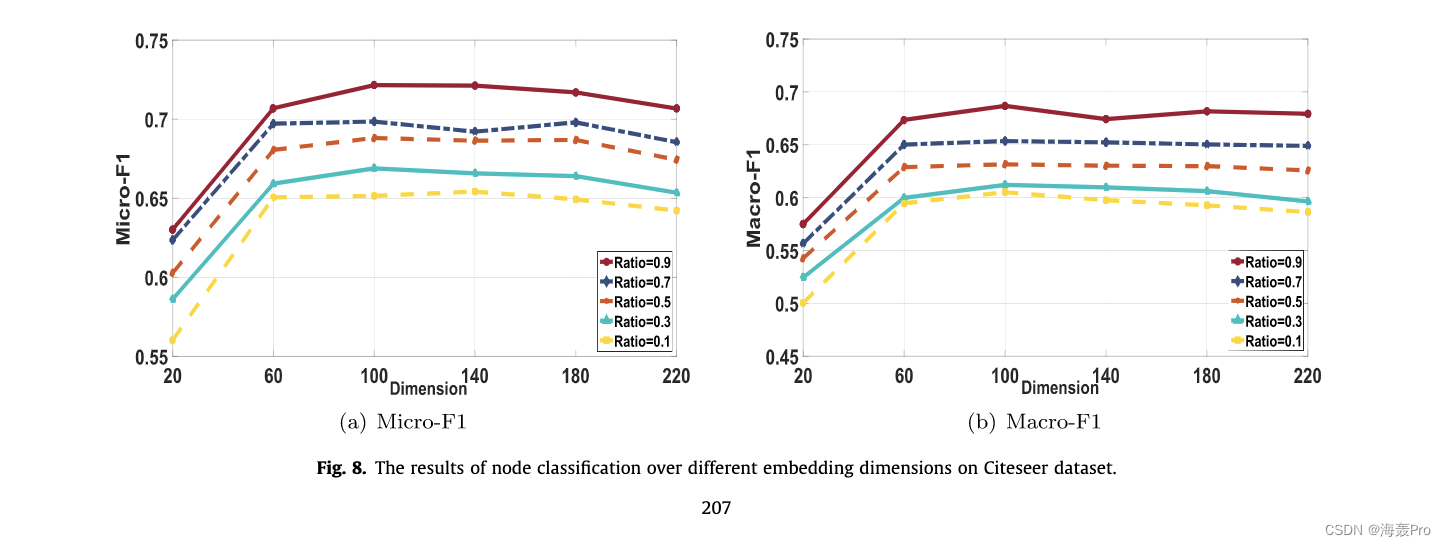
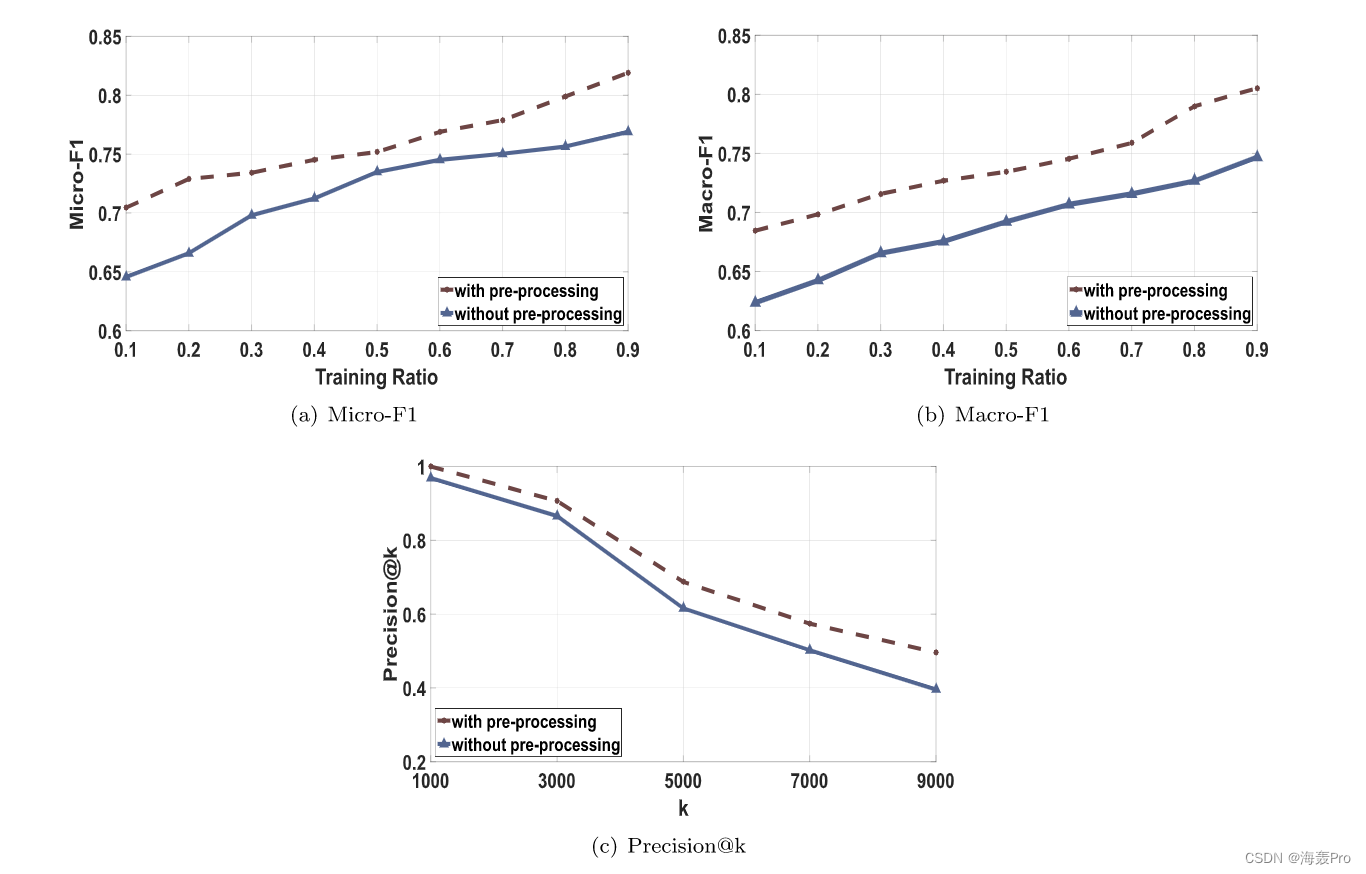
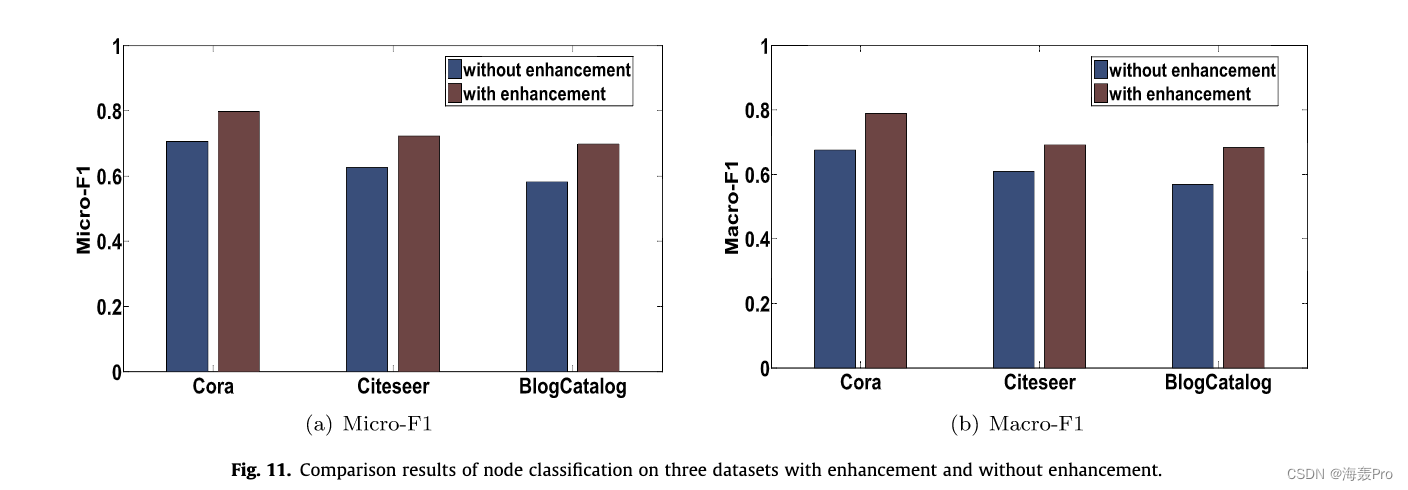
6. Conclusion

本文开发了一个深度网络嵌入框架FSADA。该框架可以在统一的框架中解决数据稀疏性、非线性结构和属性接近性的保持以及复杂关联的捕获等问题。更具体地说，我们提出了一种具有预处理过程的深度自编码器，它可以捕获非线性网络结构、节点属性以及它们之间的复杂相关性。它联合优化了二阶接近度和属性接近度的重构损失，以保持网络结构和节点属性。此外，我们实现了一个增强模块，并在节点上构造成对约束来增强潜在表示。实验结果表明，FSADA在网络重构和节点分类方面都能产生最有效的嵌入表示。

读后总结

分别对结构、属性进行编码（非线性）

然后水平拼接

再进行解码，以此得到嵌入

再对此嵌入进行一个加强操作（构造成对约束）

得到加强后的嵌入，最后再利用AE得到最终的嵌入

结语

文章仅作为个人学习笔记记录，记录从0到1的一个过程

希望对您有一点点帮助，如有错误欢迎小伙伴指正