@TOC

简介

Hello！
非常感谢您阅读海轰的文章，倘若文中有错误的地方，欢迎您指出～
 
ଘ(੭ˊᵕˋ)੭
昵称：海轰
标签：程序猿｜C++选手｜学生
简介：因C语言结识编程，随后转入计算机专业，获得过国家奖学金，有幸在竞赛中拿过一些国奖、省奖…已保研
学习经验：扎实基础 + 多做笔记 + 多敲代码 + 多思考 + 学好英语！
 
唯有努力💪
 
【每日一读】每天浅读一篇论文，了解专业前沿知识，培养阅读习惯（阅读记录 仅供参考）

论文简介

原文链接：https://ieeexplore.ieee.org/document/8807321

期刊：IEEE Transactions on Knowledge and Data Engineering ( Volume: 32, Issue: 4, 01 April 2020) （CCF A类）

年度：2020年4月1日（发表日期）

Abstract

图聚类在数据挖掘中发挥着重要作用

基于输入数据图，数据点被划分为集群

然而，大多数现有方法在聚类过程中保持数据图固定，因此它们仅限于利用隐含的数据流形并且高度依赖于初始图构造

受流形学习最近发展的启发，本文提出了一种用于图聚类的自适应一致性传播（ACP）方法

为了利用从不同角度捕获的特征，我们进一步提出了 ACP 模型（MACP）的多视图版本

主要贡献有三个：

• （1）通过从近到远传播数据点之间的拓扑连接，充分利用了输入数据的流形结构
• (2) 将图学习作为优化过程的一部分来学习聚类的最优图
• (3) 多视图聚类模型捕获异构特征之间的协商

在真实世界数据集上进行的大量实验验证了所提出的方法在单视图和多视图聚类上的有效性，并显示了它们优于最先进技术的性能

1 I NTRODUCTION

聚类是具有各种应用的数据挖掘领域的一项基础任务，在过去的几十年中吸引了许多研究人员

聚类的目的是将数据点划分为不同的聚类

为了实现这一目标，已经提出了很多方法，包括 k-means 聚类 [1]、层次聚类 [2]、谱聚类 [3]、谱嵌入聚类 [4]、最大边距聚类 [5]、支持向量聚类[6]，归一化切割[7]，多视图聚类[8]，非负矩阵分解[9]等

在现有的方法中，基于图的聚类方法（例如，Ratio-cut [10]，Normalized-cut [7 ]）由于对流形信息的利用而取得了相对较好的性能，并被广泛应用于各种应用，如图像分割[11]和蛋白质序列聚类[12]。

---

现有的大多数基于图的聚类方法[3]、[13]、[14]、[15]、[16]、[17]首先根据点的成对相似度构造数据图，然后进行图论对数据图进行优化

两阶段处理带来三个主要缺点

• 首先，在数据图中，只有邻居的相似性很大，然而，对于流形结构的数据，远点如果由连续的邻居链接，也可以保持高一致性。因此，这些方法仅限于发现底层数据结构
• 其次，一旦构建了数据图，它们在聚类期间就被固定了。那么传统方法无法学习到用于聚类的最优图，并且如果初始图的构建质量低，则往往会失败
• 第三，图论优化不能直接产生聚类结果，因此必须进行后处理（例如，k-means），这使得结果偏离最优解

最近，提出了一些方法 [18]、[19]、[20]、[21] 来解决最后两个问题

• 在优化阶段，他们自适应地更新数据图
• 通过这种方式，图学习成功地集成到了聚类过程中

受益于图学习，这些方法对初始图质量更加鲁棒

然而，这些方法仍然存在第一个问题

---

在本文中，开发了一种新的图聚类方法，即自适应一致性传播（ACP）来解决上述问题

还开发了 ACP 方法的多视图版本来处理从不同特征提取器获得的数据

本研究的主要贡献总结如下:

• 完全捕获点的拓扑一致性以研究数据流形。通过通过邻居传播一致性，该方法适用于处理具有多种结构的数据。
• 图学习被联合到聚类框架中。数据图在优化阶段进行了自适应优化，因此聚类受初始图质量的影响较小。
• 设计了所提出模型的多视图版本，该模型学习了多视图数据之间的相关性，并将它们与最佳组合进行了整合。

---

符号

• 在整篇论文中，向量被写成小写，矩阵被写成大写
• 对于矩阵M，M的第(i;j)个元素记为Mij，M的迹记为TrðMÞ
• 对于向量z，它的第i个元素记为zi，z的L2范数记为jjzjj2
• M 0 和z 0 表示M 和z 的所有元素都等于或大于零
• M 和 z 的转置分别用 MT 和 zT 表示。 I 表示单位矩阵

2 P RELIMINARY

为了获得更好的聚类性能，必须研究输入数据中隐含的流形结构 [22]

最近，一种基于传播的流形学习（PBML）方法[23]被提出用于人群运动检测，并显示出令人满意的性能

在本节中，首先重新审视 PBML 方法作为初步方法。

2.1 Propagation-Based Manifold Learning Method Revisited

Wang等人提出的基于传播的流形学习方法。 [23]旨在学习人群场景中个体的拓扑关系

给定一个个体的相似性图 G 2 Rn n（n 是个体的数量），PBML 假设具有大相似性的个体应该与任何其他点共享相似的拓扑相关性。 PBML 的目标函数定义为

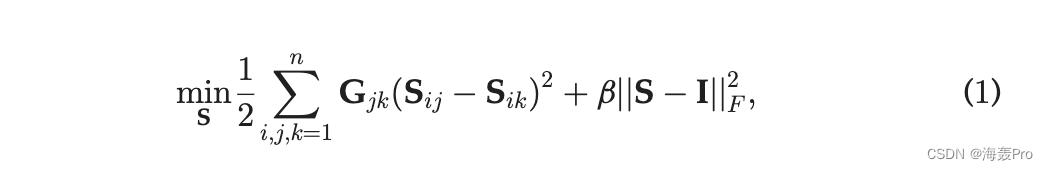
其中 S 2 Rn n 是所需的拓扑关系矩阵。在上面的等式中，如果 j 和 kare 相似，第一项确保个体 j 和 k 与个体 i 共享相似的拓扑关系。第二项阻止了平凡的解决方案，其中 S 中的所有元素共享相同的值。

根据方程式。 (1)，拓扑一致性通过相似度高的邻居传播，那么远的个体如果被连续的邻居联系起来，就会保持密切的关系。它在人群运动检测方面表现良好。然而，得到的拓扑关系矩阵 S 并没有表明明确的簇结构，因此需要进行后处理将点划分为簇。此外，它不能利用聚类数的先验，这在图聚类文献中总是给出。因此，PBML 方法不能直接用于聚类任务。

3 ADAPTIVE CONSISTENCY P ROPAGATION

在本节中，我们将 PBML 方法扩展到图聚类领域，并提出了自适应一致性传播方法。

3.1 Methodology

正如 Mohar 等人指出的那样。 [24]，如果图 S 2 Rn n 的拉普拉斯矩阵 LS 的秩为 n c，则图 S 2 Rn n 将包含恰好 c 个连通分量。假设点数为n，期望的簇数为c，则数据图S可以看作是一个指示矩阵，其中来自同一簇的点连接到同一个分量中

根据最近的图聚类方法[18]、[19]、[20]、[21]，如果我们在等式上施加约束rankðLS Þ 1/4 n c。 (1)、一旦得到最优S即可完成聚类任务，无需进行后处理。所以目标可以定义为

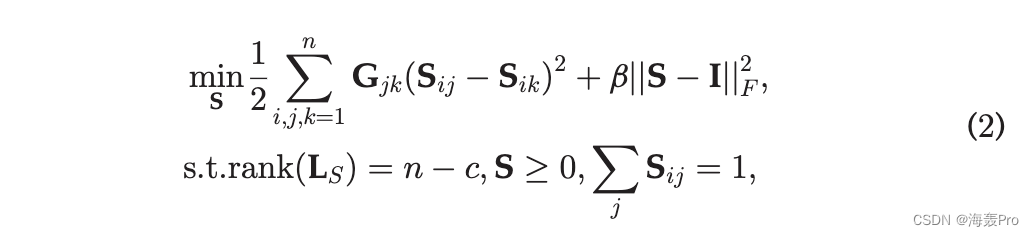
其中 LS 是 S 的拉普拉斯矩阵

然后在问题 (2) 中成功地利用了先验簇数 c。我们还约束 S 的每一行之和为 1，并且 S 的每个元素都是非负的。在问题（2）中，如果点 j 与许多相似的邻居相连，则会在很大程度上影响目标值。为了平等对待每个点，我们提出了等式的标准化版本。 (2) 如下：

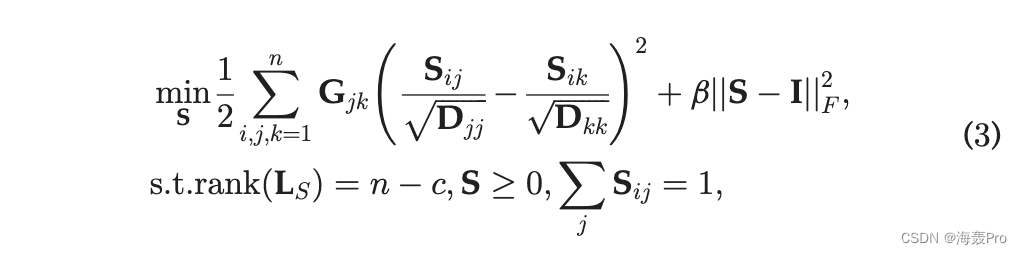
其中 D 是 G 的度矩阵。

问题 (3) 很难解决，因为等级约束取决于 S。As Nie 等人。 [18] 指出，rankðLS Þ 1/4 n c 等价于 Pc i1/41 siðLS Þ 1/4 0，其中 siðLS Þ 是 LS 的第 i 个最小特征值。则问题（3）转化为

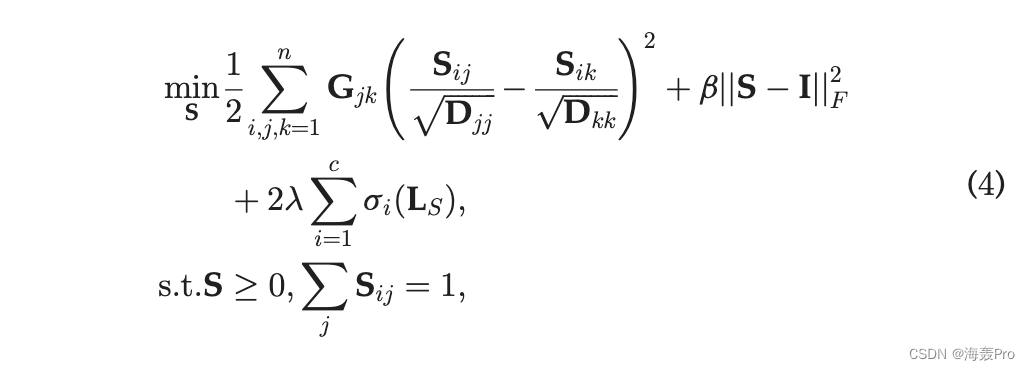
其中是一个足够大的参数来强制执行 Pc i1/41 siðLS Þ 1/4 0。

---

根据 Ky Fan 定理 [25]，我们有

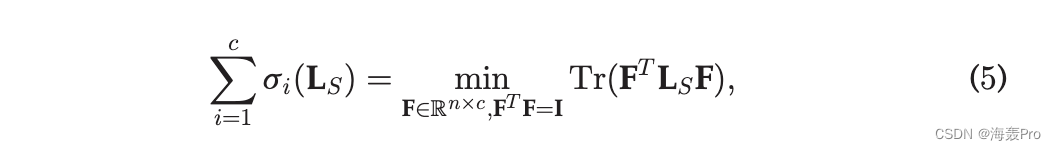
其中 F 是一个正交向量，它使 TrðFT LS FÞ 的值最小化。

结合方程式。 （4）和（5），我们得到以下问题

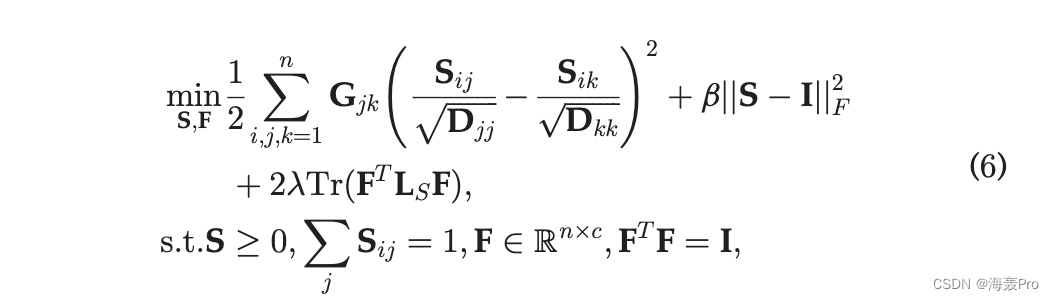
与问题（4）相比，这更容易解决。

在等式。 （6），图S通过邻居传播一致性，如果远点被相似点连接，则将它们拉到一起。此外，聚类结构在 S 中明确表示。因此，可以将所需的 S 视为聚类指标。一旦学习了最优S，就得到了最终的聚类结果。在接下来的部分中，提出了一种交替方法来解决问题（6）并自适应地学习最优 S。

4 M ULTI-V IEW A DAPTIVE C ONSISTENCY P ROPAGATION

在现实世界的应用程序中，对象可以从多个视图中表示。例如，在计算机视觉中，图像可以用不同的特征来描述，例如 SIFT [27]、HOG [28] 和 CENT [29]。每个特征捕获一个特定的统计属性，需要整合这些异构特征并利用互补信息。在本节中，我们提出了 ACP 模型 (MACP) 的多视图版本。

6 DISCUSSION

在本节中，我们研究了参数在 ACP 和 MACP 中的影响

如上所述，参数是通过启发式方式自动确定的，所以我们只讨论参数 b 的影响，它控制方程中平滑项和拟合项的平衡。 (6) 和 (16)

当我们将 b 的值从 f1、5、10、15、20、25g 变化时，聚类精度的方差如图 1 所示

如图所示，ACP 和 MACP 的性能对值不是很敏感b。所以我们在实验中简单地将 b 设置为 1。

7 CONCLUSION

在本文中，提出了自适应一致性传播及其多视图版本 MACP 用于聚类

大多数传统方法只关注具有相邻关系的数据点，并在优化过程中保持数据图不变

在我们的新方法中，局部一致性从近到远自适应地传播，因此来自同一簇的点可以全部拉到一起

此外，在合理的约束条件下，ACP 和 MACP 能够学习聚类的最优图，无需任何后处理即可同时完成聚类。单视图和多视图聚类的综合实验表明我们的方法在各种数据集上的优越性能

结语

文章仅作为个人学习笔记记录，记录从0到1的一个过程

希望对您有一点点帮助，如有错误欢迎小伙伴指正