二叉树中和为某一值的路径(一)(二)(三)(剑指offer)

二叉树中和为某一值的路径(一)

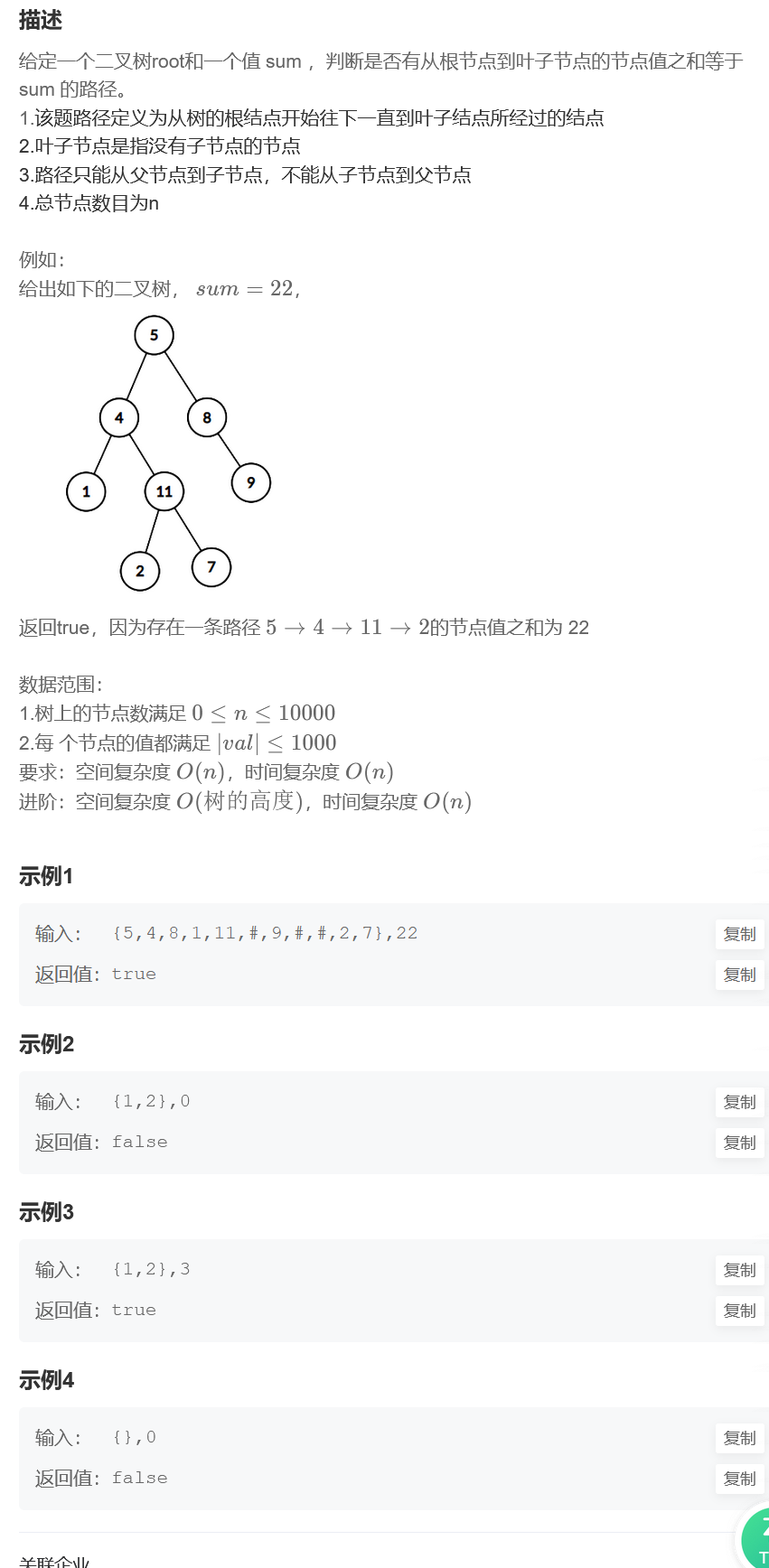
  //方法一:递归前序遍历
    public boolean hasPathSum (TreeNode root, int sum) {
        //路径不存在,出口!
         if(root==null) return false;
          //处理当前节点!
         sum-=root.val;//更新值!
        if(sum==0&&root.left==null&&root.right==null)
            return true;
        //遍历左右子树
        return hasPathSum(root.left,sum)||hasPathSum(root.right,sum);
    }

//层序遍历(关键每一层中的节点有不同的路径和,所以构造了一个内部类记录不同节点的路径和)
//内部类和路径相关联!
,    class Pair{
        TreeNode curNode =null;
        int curVal = 0;//记录当前路径和!
        public Pair(TreeNode curNode,int curVal){
            this.curNode = curNode;
            this.curVal = curVal;
        }
    }
    public boolean hasPathSum (TreeNode root, int sum) {
        // write code here
        //方法二:层序遍历
        //借助队列!
        if(root==null) return false;
        Queue<Pair> queue = new LinkedList<>();
        queue.offer(new Pair(root,root.val));
        while(!queue.isEmpty()){
                Pair cur = queue.poll();
                if(cur.curNode.left!=null){//左节点入队
                    queue.offer(new Pair(cur.curNode.left,cur.curVal+cur.curNode.left.val));
                }
                if(cur.curNode.right!=null){//右节点入队
                    queue.offer(new Pair(cur.curNode.right,cur.curVal+cur.curNode.right.val));
                }
                if(sum==cur.curVal&&cur.curNode.right==null&&cur.curNode.left==null){
                    return true;
                }
        }
        return false;
    }

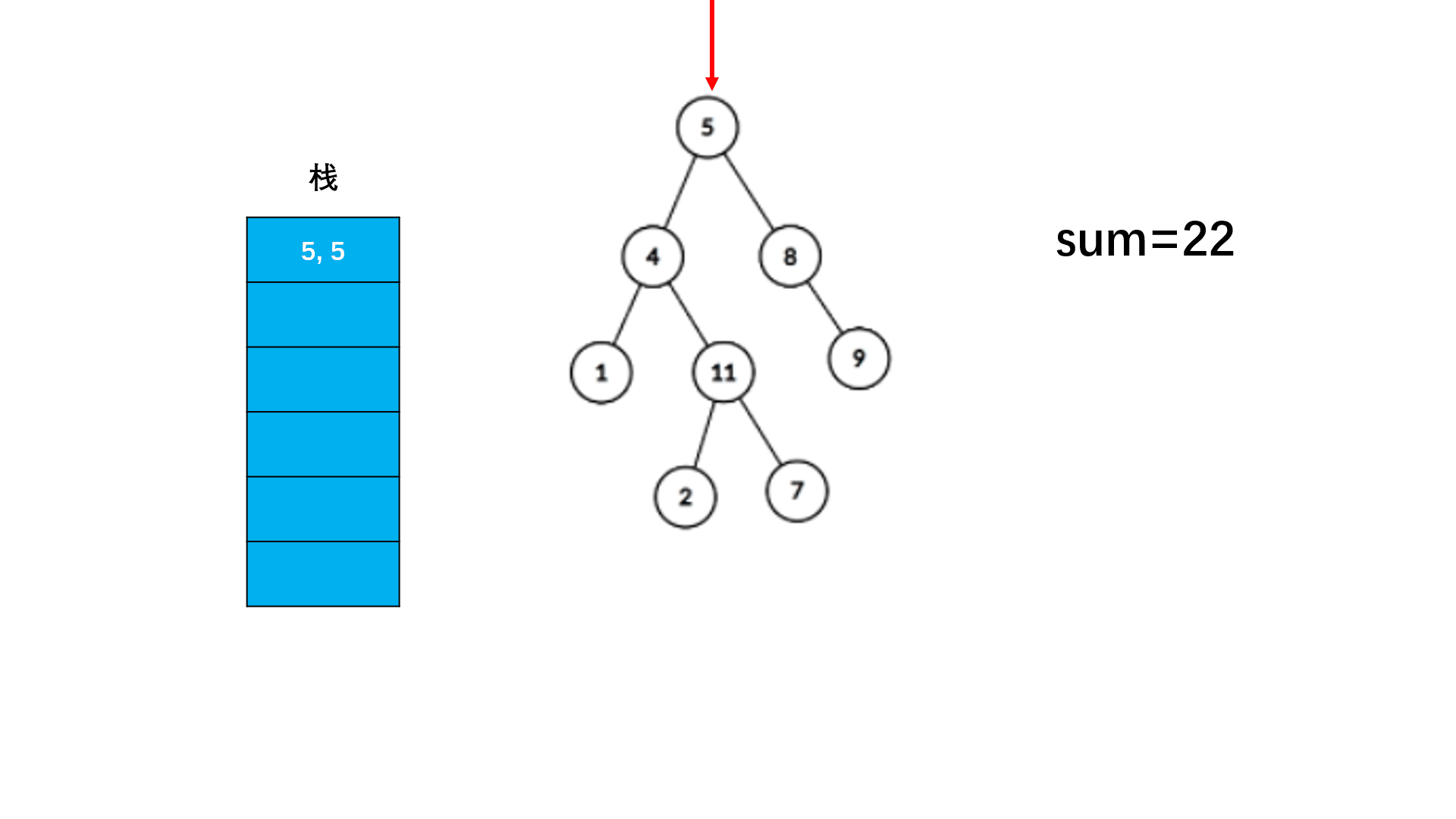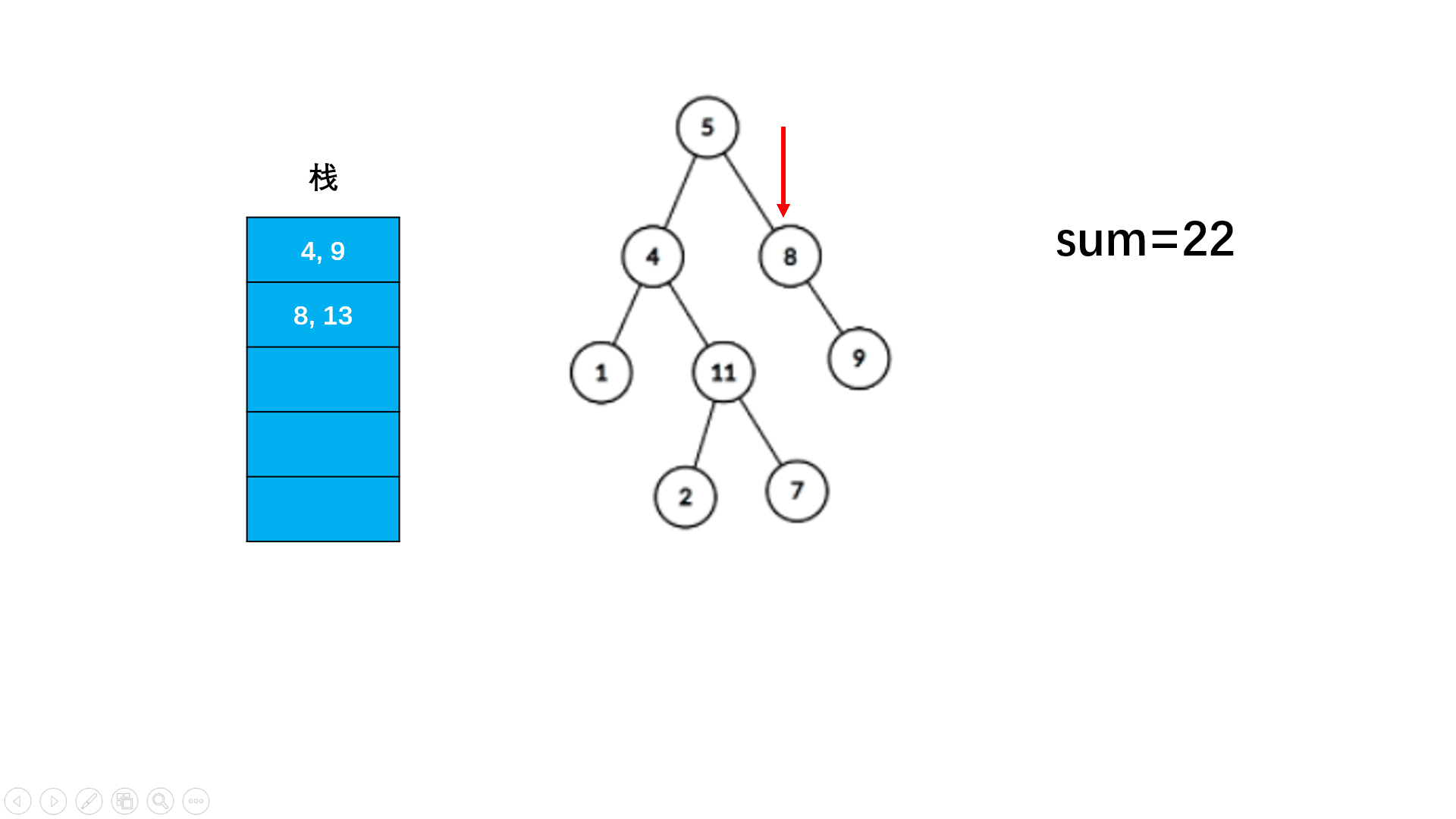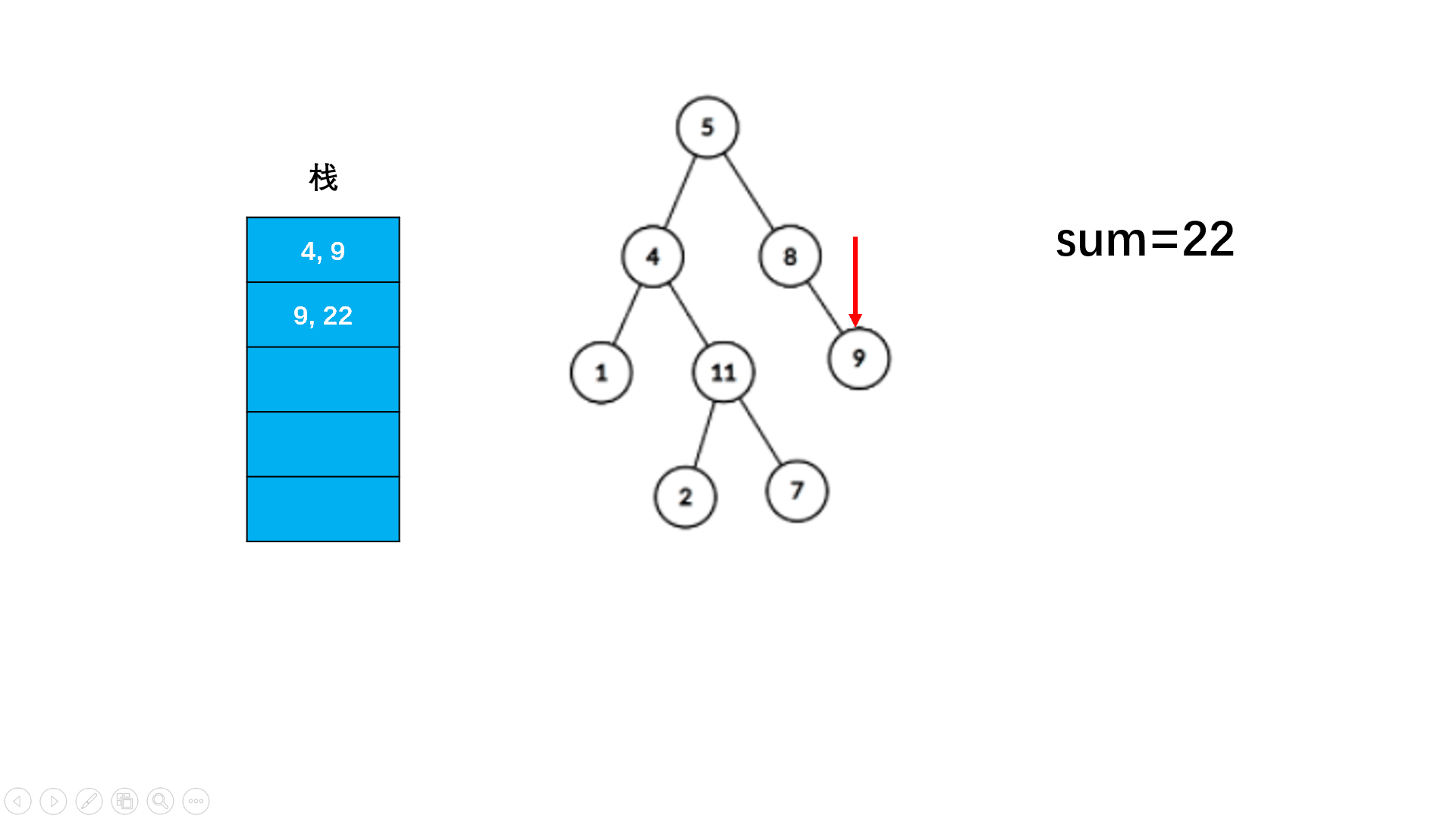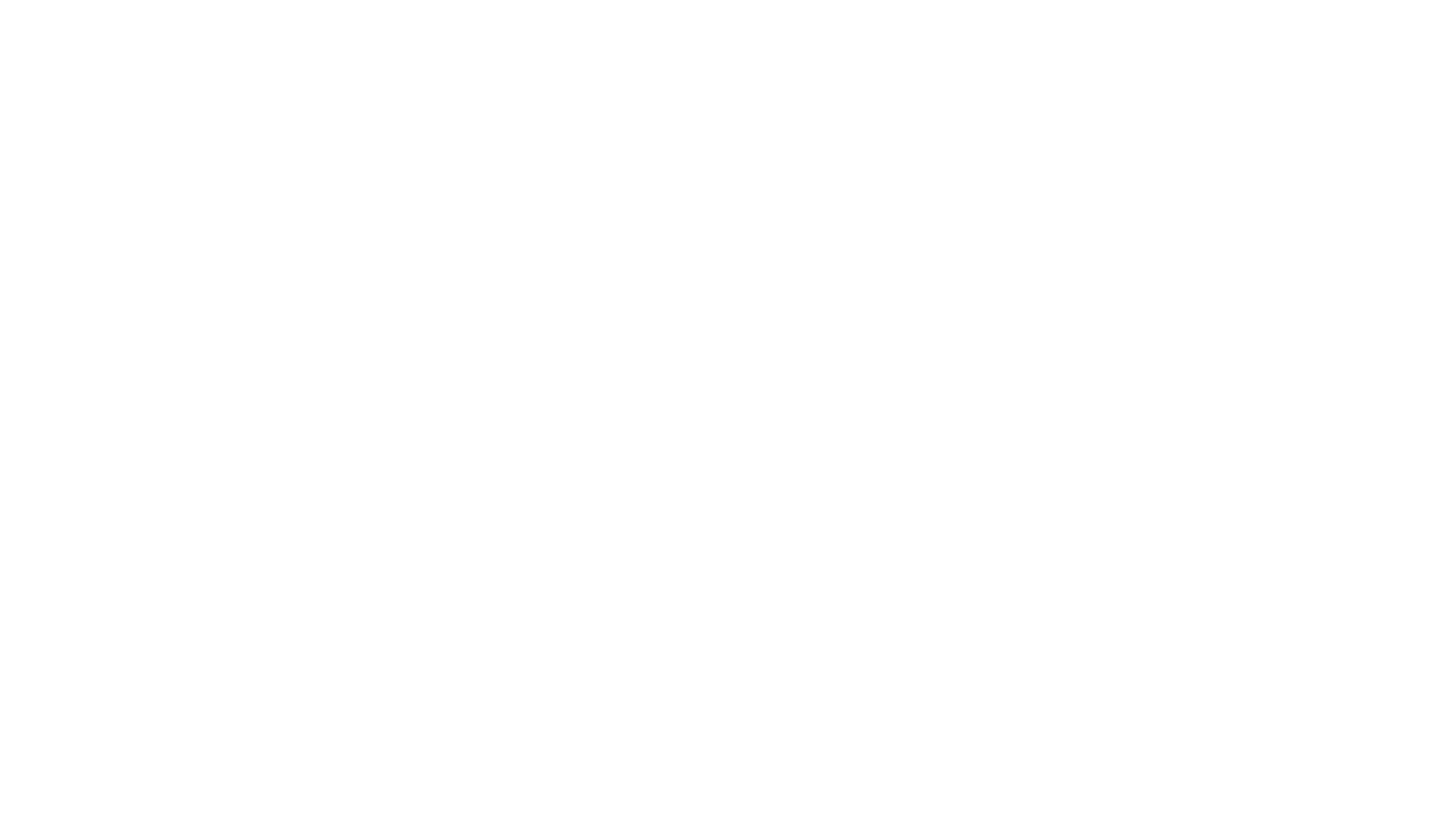
//非递归  
public boolean hasPathSum (TreeNode root, int sum) {
        // write code here
        //利用两个栈,一个栈存当前路径和,一个用于深度优先遍历!
        if(root==null) return false;
        Stack<TreeNode> stack1 = new Stack<>();
        stack1.add(root);
        Stack<Integer> stack2 = new Stack<>();
        stack2.add(root.val);
        while(!stack1.isEmpty()){
            TreeNode cur = stack1.pop();
            int curVal = stack2.pop();
            if(sum==curVal&&cur.left==null&&cur.right==null){
                return true;
            }
            if(cur.left!=null){
                //将左节点和对应的路径和入栈!
                stack1.push(cur.left);
                stack2.push(curVal+cur.left.val);
            }
             if(cur.right!=null){
                //将右节点和对应的路径和入栈!
                stack1.push(cur.right);
                stack2.push(curVal+cur.right.val);
            }
        }
        return false;
    }

• 这里采用两个栈,一个用于存节点,一个用于存对应路径和, 和刚刚通过层序遍历用Pair保存当前路径和作用类似!

二叉树中和为某一值的路径(二)

题目链接

描述:

这题和1一样,这里只不过需要借助数组集合保存结果集即可!

//回溯!
public class Solution {
    public ArrayList<ArrayList<Integer>> FindPath(TreeNode root,int expectNumber) {
       //这里采用回溯,深度优先遍历!
        //关键就是当访问某一子树后,回到该处时需要将该节点除去!
        ArrayList<ArrayList<Integer>> result = new ArrayList<>();
        if(root==null) return result;
        ArrayList<Integer> tmp = new ArrayList<>();
        FindPathHelp(root,expectNumber,0,result,tmp);
        return result;
    }
    
    public void FindPathHelp(TreeNode root,int expectNumber,int sum,ArrayList<ArrayList<Integer>> result,ArrayList<Integer> tmp){
        //出口,返回!
        if(root==null){//不满足,回退到上一层
            return;
        }
        //处理这一节点!
        tmp.add(root.val);
        sum += root.val;
        //检查是否满足条件!
        if(sum==expectNumber&&root.left==null&&root.right==null){
            result.add(new ArrayList<>(tmp));
            tmp.remove(tmp.size()-1);//tmp.remove ,return 二选一!
            return;
        }
        //处理下一层
        FindPathHelp(root.left,expectNumber,sum,result,tmp);
        FindPathHelp(root.right,expectNumber,sum,result,tmp);
        //回退!
        tmp.remove(tmp.size()-1);
        return;
    }
}

注意:

• 这里本层结果的判断不能在其左右节点判断

if(sum==expectNumber&&root==null)这样结果会重复添加2次!

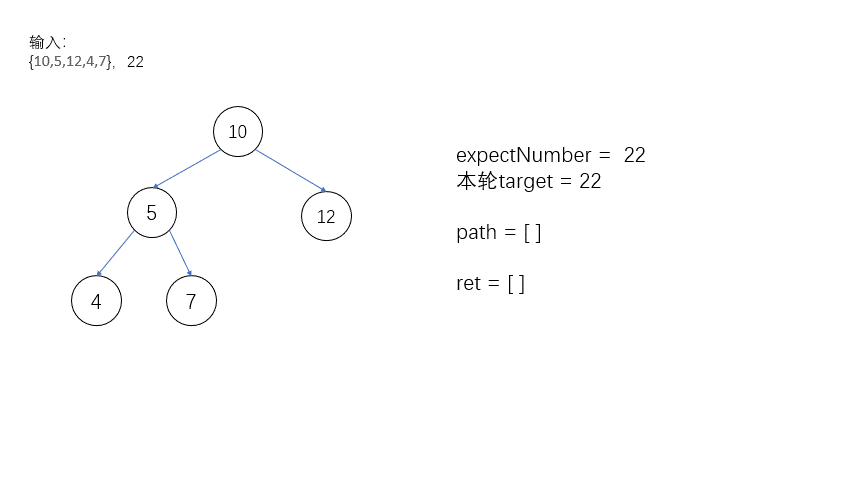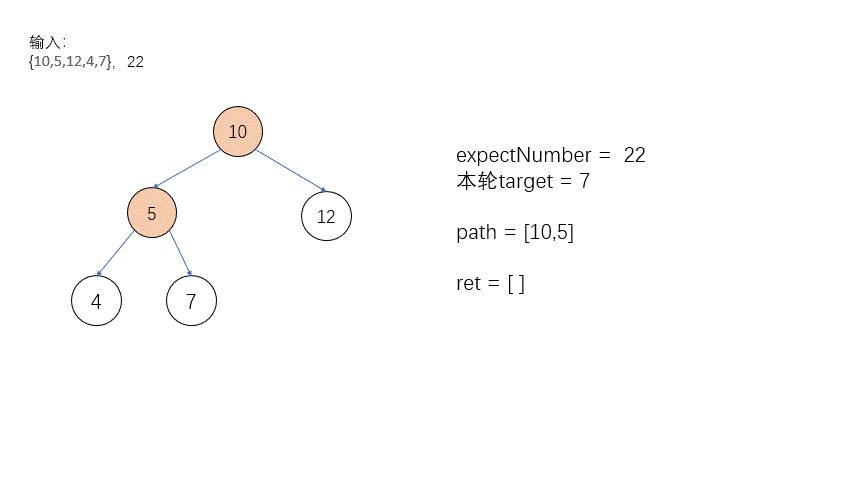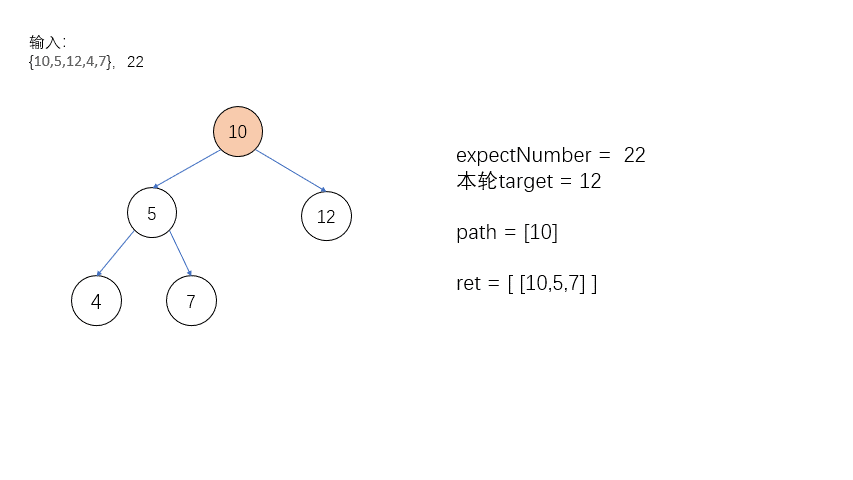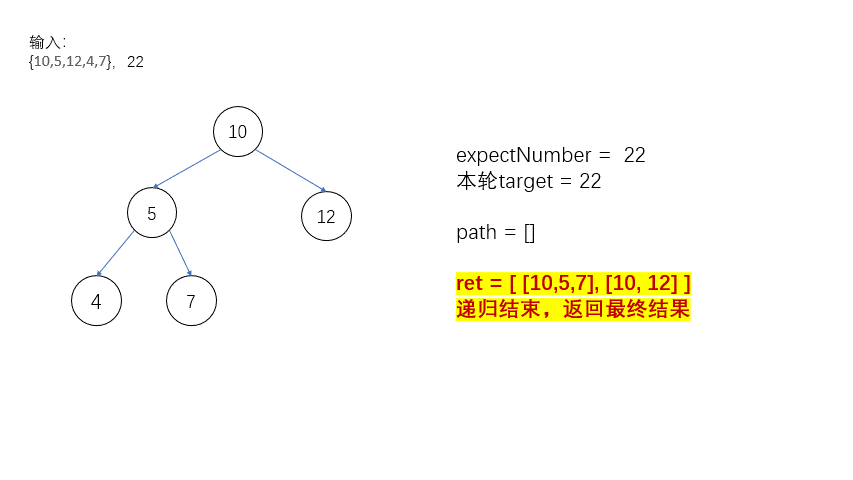
如图就是一整个回溯的过程!

二叉树中和为某一值的路径(三)

题目链接

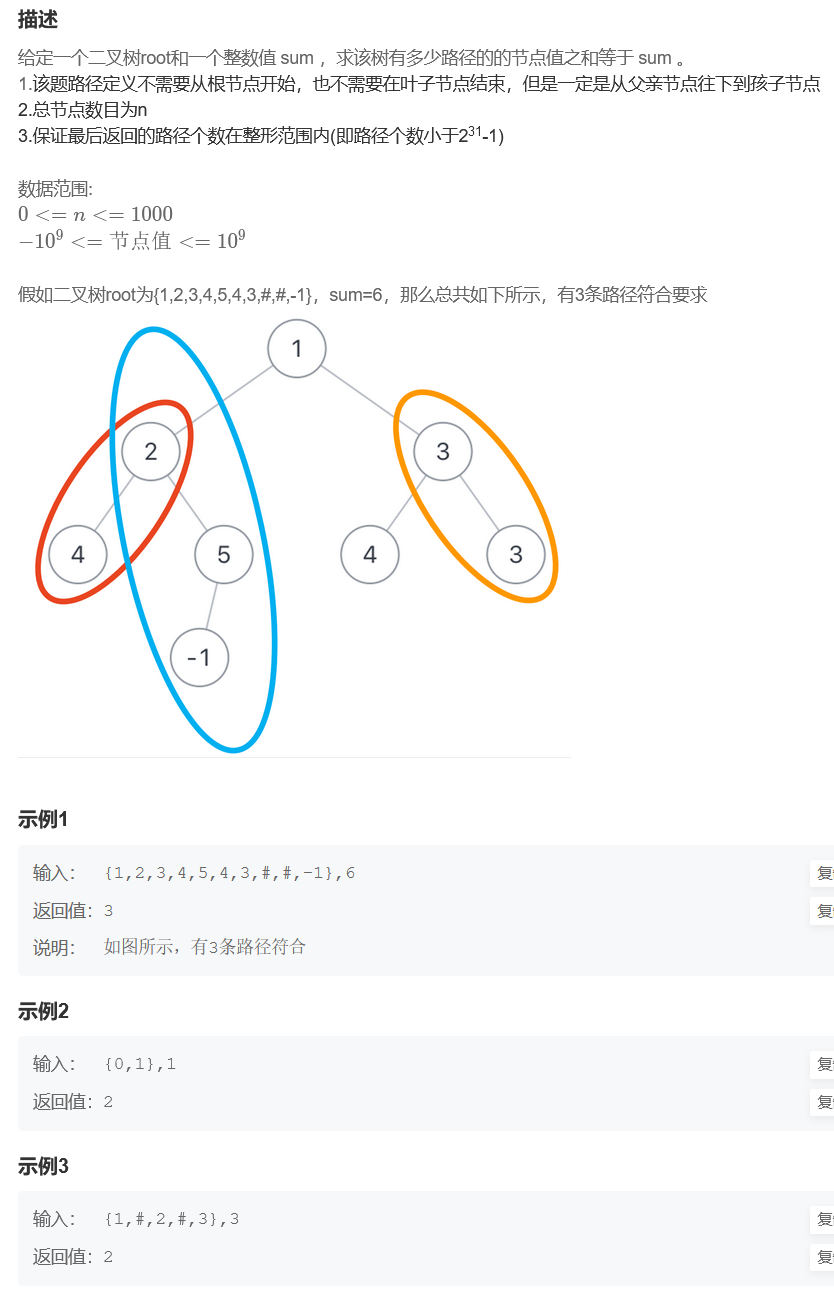
• 我们这里遇到的问题就是需要确定路径的开始位置根!
• 如果根确定了就转化成了上面的问题,所以我们可以通过递归来进行遍历根,达到路径起点不同的效果!
  • 所以这里的一层递归,加上上述递归!就通过两层递归解决了这个问题!

//两层递归! 
private int ret = 0;
    private void dfs(TreeNode root,int sum){
        if(root==null) return;
        sum -= root.val;
        if(sum==0) ret++;
        dfs(root.left,sum);
        dfs(root.right,sum);
        sum +=root.val;
        return;
    }
    public int FindPath (TreeNode root, int sum) {
        // write code here
        //二叉递归
        //一次递归根节点,第二次判断以该根节点为起始节点是否有匹配路径!
        //递归遍历该树,前序遍历避免了回溯了
        if(root==null) return ret;
        //计算该根起始匹配路径!
         dfs(root,sum);
        //遍历左右!
         FindPath(root.left,sum);
         FindPath(root.right,sum);
        return ret;
    }

• 时间复杂度:O(n^2)两层递归!
• 空间复杂度:O(n)每层递归最深就只有n

我们也可以通过递归+哈希解决这个问题!

我们这里最重要的就是实现路径起始节点的移动!

我们可以通过哈希表保存每条路径和出现的次数!

如果当到达一个节点后, 该节点位置的值加上上一层的路径和 - sum的值在hash表中,说明前面位置的位置的值可以用这个节点值代替,所以将hash表中的这个路径出现次数加在 res中!

这个方法不太好理解…

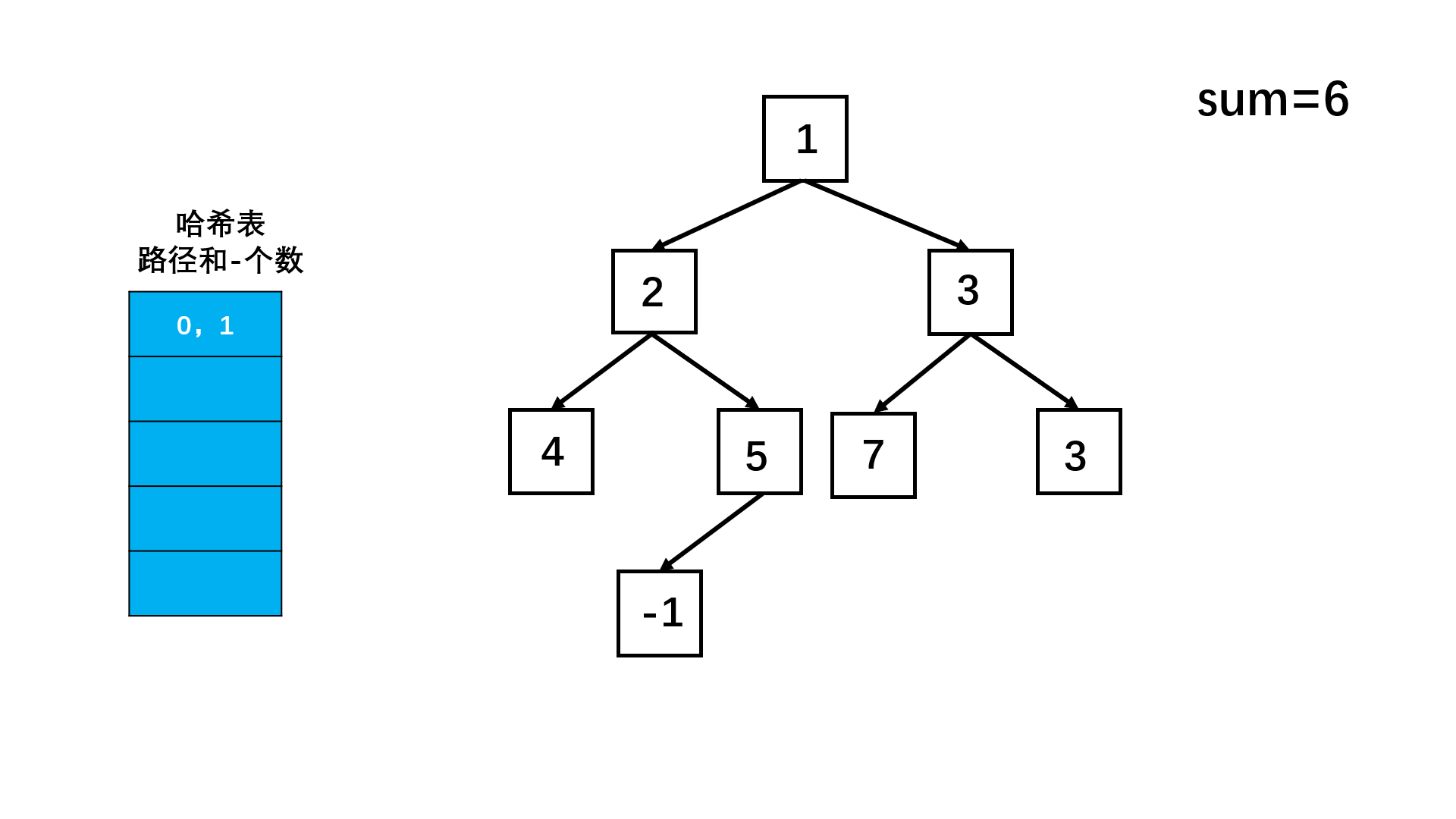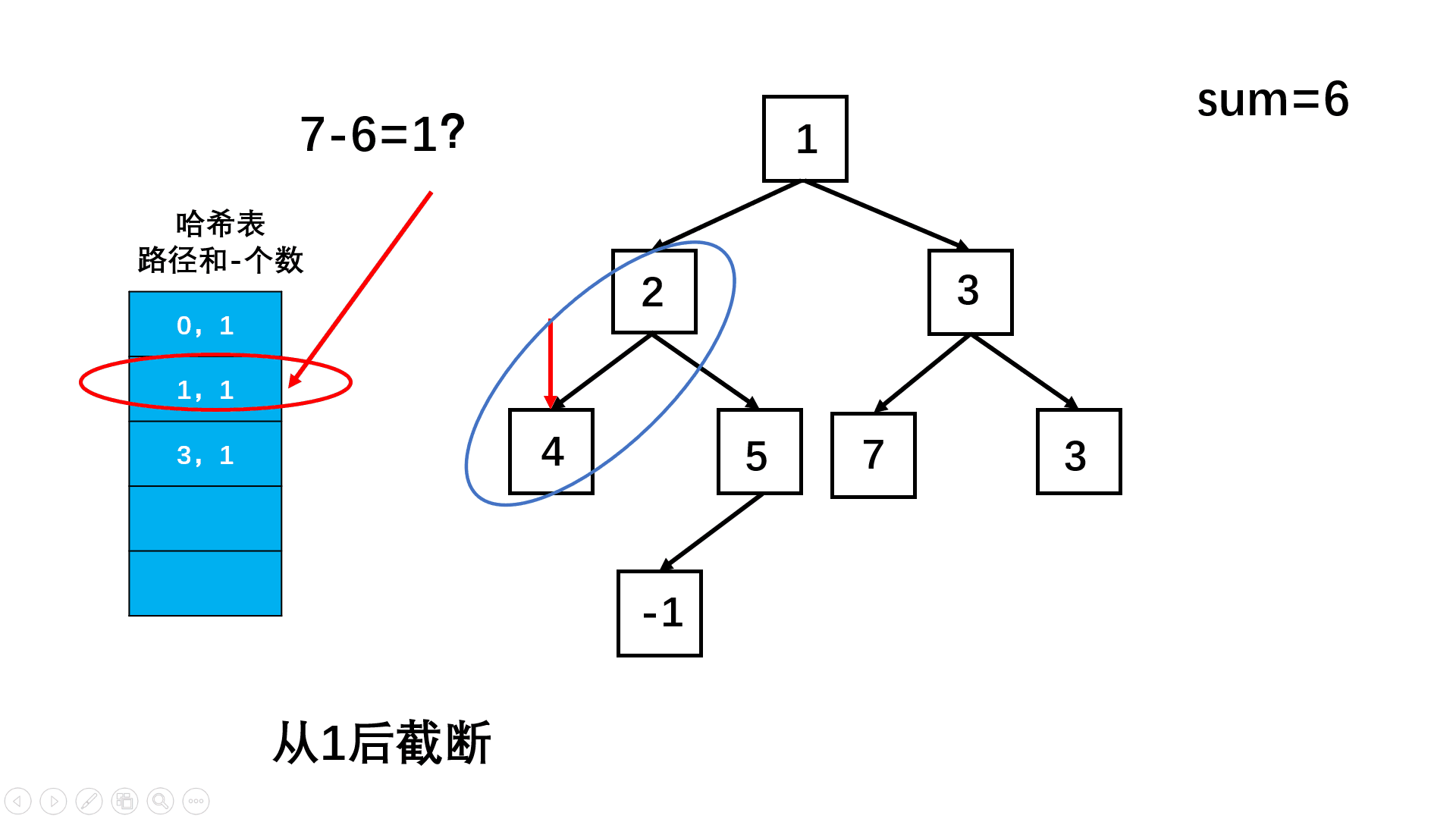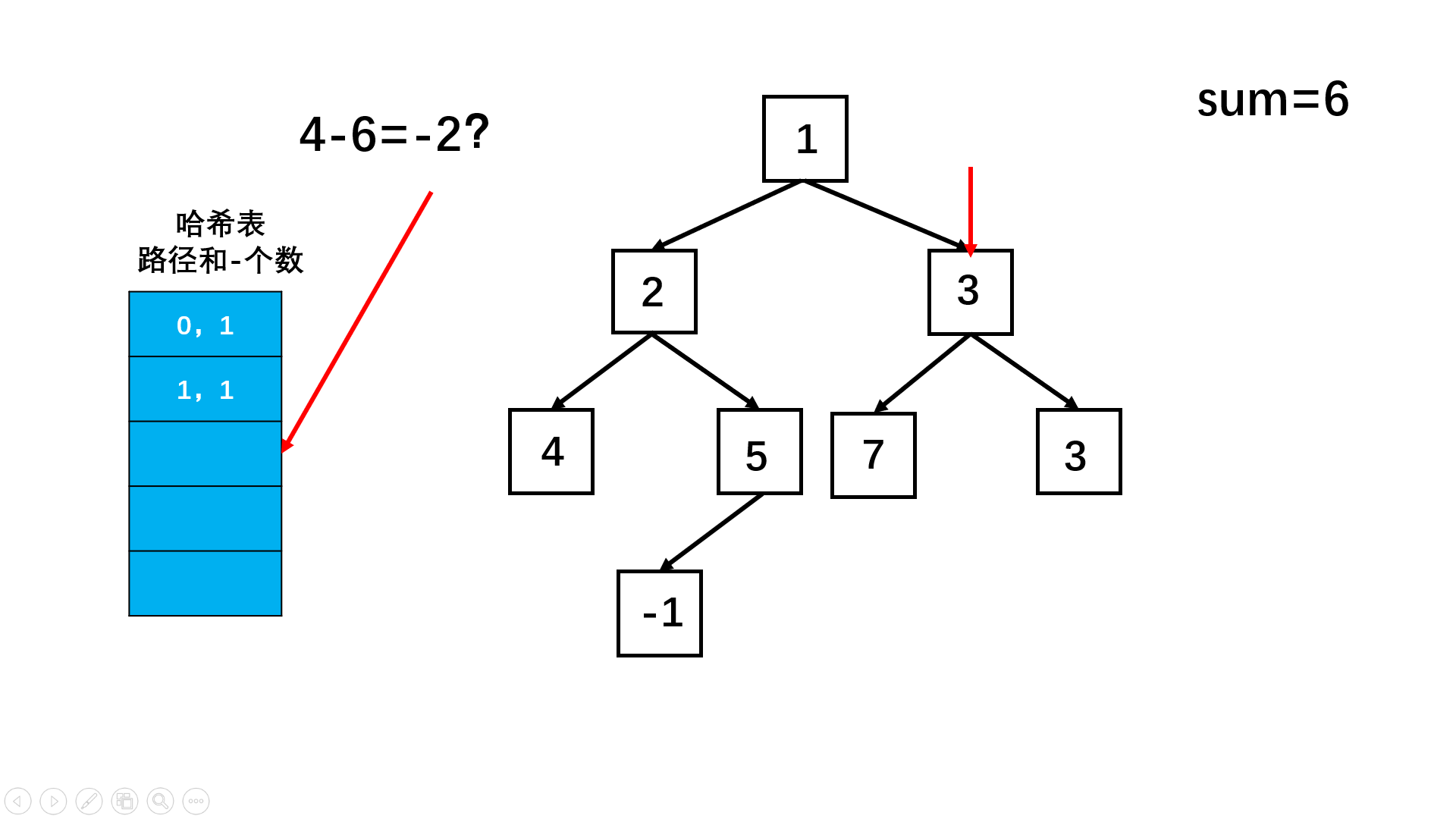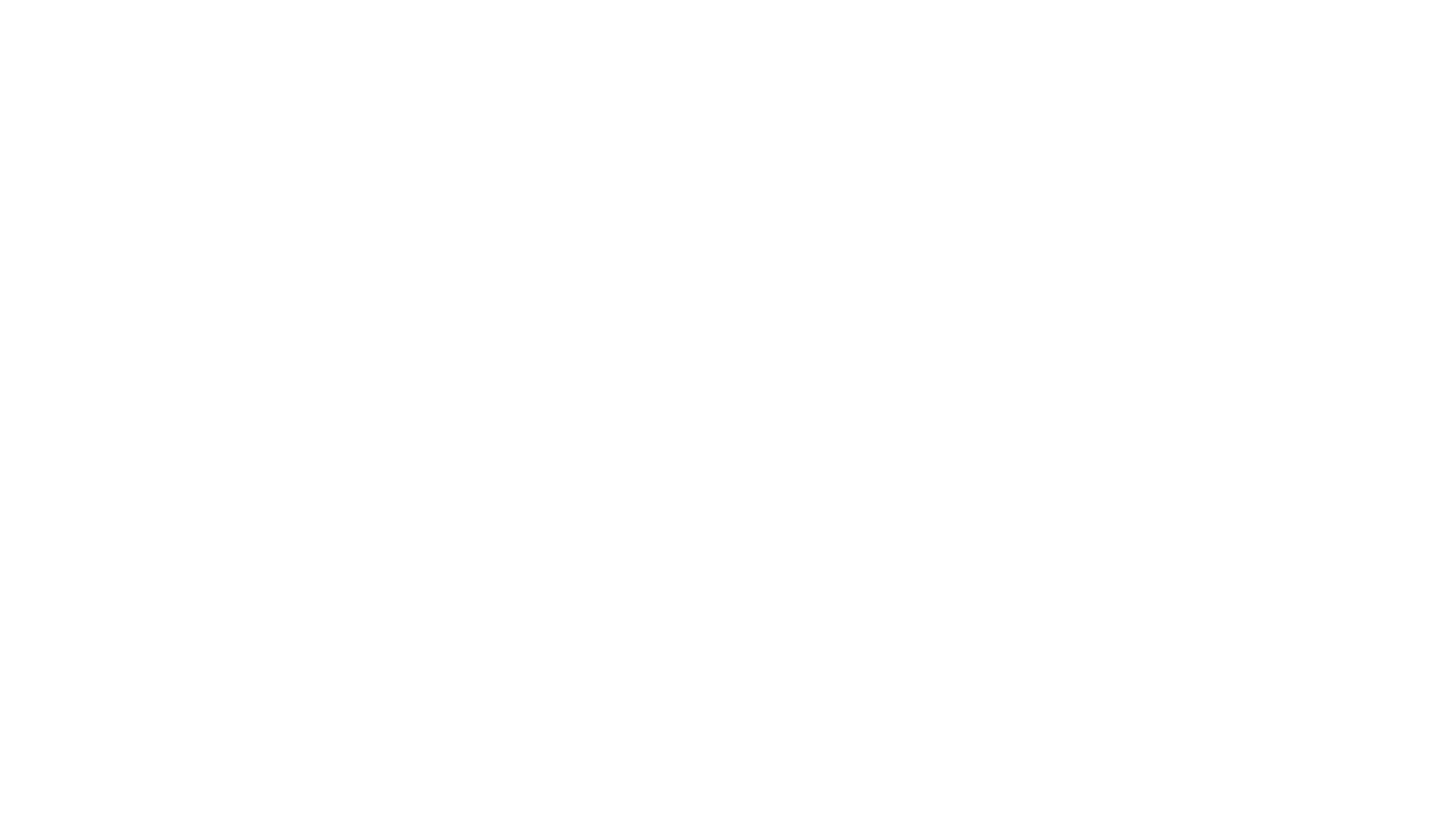
 private HashMap<Integer,Integer> mp = new HashMap<>();
    //上层路径和:last
    public int dfs(TreeNode root,int sum, int last){
        if(root==null) return 0;
        int res = 0;
        //到该节点路径和!
        int tmp = root.val + last; 
        //如果该路径和减去sum在哈希表中出现过,想当于减支!
        //也就是这个节点的效果等同于上面路径的某和,所以就需要下移,去掉前面的!
        if(mp.containsKey(tmp - sum)){
            //加上这个路径和出现的次数!
            res +=mp.get(tmp - sum);
        }
        //增加该路径和
        mp.put(tmp,mp.getOrDefault(tmp,0)+1);
        res += dfs(root.left,sum,tmp);
        res += dfs(root.right,sum,tmp);
        //回退!
        mp.put(tmp,mp.get(tmp)-1);
        return res;
    }
    public int FindPath (TreeNode root, int sum) {
        // write code here
        mp.put(0,1);
        return dfs(root,sum,0);
    }

• 时间复杂度：O(n)，其中n为二叉树的结点数，遍历一次二叉树，哈希表的操作都是O(1)
• 空间复杂度：O(n)，哈希表大小及递归栈最大为n