@TOC

简介

Hello！
非常感谢您阅读海轰的文章，倘若文中有错误的地方，欢迎您指出～
 
ଘ(੭ˊᵕˋ)੭
昵称：海轰
标签：程序猿｜C++选手｜学生
简介：因C语言结识编程，随后转入计算机专业，获得过国家奖学金，有幸在竞赛中拿过一些国奖、省奖…已保研
学习经验：扎实基础 + 多做笔记 + 多敲代码 + 多思考 + 学好英语！
 
唯有努力💪
 
【每日一读】每天浅读一篇论文，了解专业前沿知识，培养阅读习惯（阅读记录 仅供参考）

论文简介

原文链接：https://dl.acm.org/doi/10.1145/3488560.3498467

会议：WSDM '22: Proceedings of the Fifteenth ACM International Conference on Web Search and Data Mining （CCF B类）

代码：https://github.com/marhar19/GAGE-Geometry-Preserving-Attributed-GraphEmbeddings

年度：2022年2月15日

ABSTRACT

节点嵌入是提取网络中连接的某些实体的简洁和信息表示的任务

各种现实世界的网络以特征或时间序列数据的形式包含有关节点连接性和某些节点属性的信息

现代表示学习技术利用节点的连接性和属性信息以无监督的方式生成嵌入

在这种情况下，非常需要导出保留网络几何形状和属性向量的嵌入，因为它们将反映拓扑邻域结构和特征空间中的邻近性

虽然仅在观察网络的连通性或属性信息时保持这一点相当简单，但保留这两种信息的几何形状是具有挑战性的

同时保留两种信息 还是挺困难的

本文提出了一种用于属性网络中节点嵌入的新型张量分解方法，该方法保留了连接和属性的距离

此外，开发了一种有效且轻量级的算法来解决学习任务，并且具有多个最先进基线的明智实验表明，所提出的算法在下游任务中提供了显着的性能改进

1 INTRODUCTION

网络科学通过观察它们之间的相互作用来研究属于一个或多个社区的实体的行为[3]。网络和网络科学在科学和工程领域引起了相当大的关注，因为它们提供了各种物理、社会和工程系统的优雅抽象——以及分析它们的有效工具[12、25]。如今，网络在众多科学和工程学科中无处不在，包括社会、通信和生物网络，仅举几例。

网络通常由图表示，图是信息抽象并对系统中的交互进行建模。特别是，图表示通过一组边对不同实体（节点）的连接信息进行编码。网络中的连接信息很重要，它描述了网络中相对于其余节点的每个节点。在现实世界的网络中，实体不仅由它们与其他实体的连接性来定义，而且还可以由一组测量值或属性来描述，这些测量值或属性提供了单个级别的节点表征，并且通常信息量很大。尽管图提供了网络实体的优雅表示，但也需要实体的单独表示，这不一定由与社区子集的关系来描述。此外，当每个节点的属性都可用时（这在实践中通常是这种情况），必须将连接性和属性信息结合在一个单一的、通用的表示中，尽可能多地封装信息。此外，各种有趣的网络涉及数百万个节点，这使得节点的图形表示对于某些任务非常不切实际。

上述挑战强调了网络节点的简洁和信息表示的必要性，这有利于探索性分析以及下游应用程序。这激发了大量关于在低维向量空间中嵌入图节点的研究，以无监督的方式使用图和属性信息。该任务也称为无监督节点或图表示学习。无监督节点嵌入的目标是双重的。一方面，嵌入应该捕获图形和属性中存在的最大数量的知识，以避免信息丢失。为此，成功节点嵌入的关键是能够保留网络的几何形状，由节点的连接性和属性的接近度定义。另一方面，嵌入应该能够提高各种下游网络任务的性能，例如节点分类、链接预测和社区检测等。嵌入算法产生的简洁节点表示可以显着受益于基于特征的工具，例如逻辑回归、支持向量机，甚至神经网络——尤其是当只能访问有限的训练数据时。

已经提出了大量的方法来执行节点嵌入。早期的工作仅使用网络的连接信息来处理节点表示学习任务。他们中的一些人专注于正确定义连接信息的相似性度量并对其执行矩阵分解[1、4、5、26、29、32、34、36、39]。 [20] 中的工作执行耦合张量矩阵分解以在知识图的上下文中学习表示。随机游走也已成功用于生成节点嵌入，例如 [16, 27]。最近，研究的重点已经转移到为属性网络生成嵌入。[39] 中的工作将 deepwalk [27] 推广到属性可用的情况，而 [19] 在半监督设置中执行标签通知属性节点表示学习。用于网络科学任务的神经网络最近也受到了广泛关注。特别是，图卷积神经网络和图自动编码器在属性节点嵌入方面非常流行[6、10、13、21、22、37、38]。还提出了执行归纳嵌入的工作，例如 [17, 37]，其中使用多个图训练图卷积网络。最后，[2]中的工作采用了一个张量分解模型，并将传统的邻接关系与属性的𝑘-nearest邻居矩阵联合因式分解。

我们的工作受到以下问题的启发：我们能否生成节点嵌入，以便我们可以证明保留以下几何形状：

• 1）与网络的连接信息相关的距离
• 2）与网络的属性信息相关的距离，在无人监督的方式？

这是一个很好的问题，因为维护网络几何是表示学习的基本目标，并且正如我们将在本文中展示的那样，这样做可以显着提高几个下游任务的性能

这个问题可以非正式地表述如下：

• 给定:网络节点的连通性和属性信息。
• 产生:保留连接性和属性几何结构的低维节点表示。

我们提出了保持几何的属性图嵌入(GAGE)——一种以无监督方式提取节点嵌入的原则性方法

GAGE有几个有利的特性。

• 通过设计，生成的嵌入保留了节点的几何形状，这是从节点邻接矩阵和节点属性推断出来的。
• 节点嵌入是唯一的，因此排列不变，这意味着在邻接表示法中对节点的任何重新排序都会产生相同的嵌入。
• 该方法既适用于无向网络，也适用于有向网络。
• 该方法灵活，不需要每个节点的连通性和属性信息;可以为部分/完全缺少连通性或属性信息(但不能同时缺少两者)的节点生成嵌入。
• 该算法具有轻量级和可扩展性，能够有效地处理大型网络。

为了评估GAGE的性能，我们使用了三个真实的属性网络基准

实验结果表明，GAGE在这两个任务中都有很大的前景，显著优于基线

我们的工作贡献可以概括如下:

• 新颖的问题表述:该领域之前的工作没有形式化直观的需求，即嵌入应该能够(近似地)再现与连接性和属性信息相关的距离。
• 分析:我们表明，通过利用张量分解和多维缩放的有利特性，所提出的嵌入可以(近似地)再现连通性和属性距离。
• 算法:提出了一种新的张量因子分解算法来执行无监督嵌入任务。该算法利用了张量的特殊结构，具有快速、可扩展的特点，适用于大型网络。
• 实验验证:提出的方法在节点分类和链路预测设置下进行了评估，并在这两个任务中显示出非常有希望的结果。

可重复性:我们使用的数据集都是公开的;代码和数据可以在以下链接中找到

表示法:表1总结了我们的表示法。

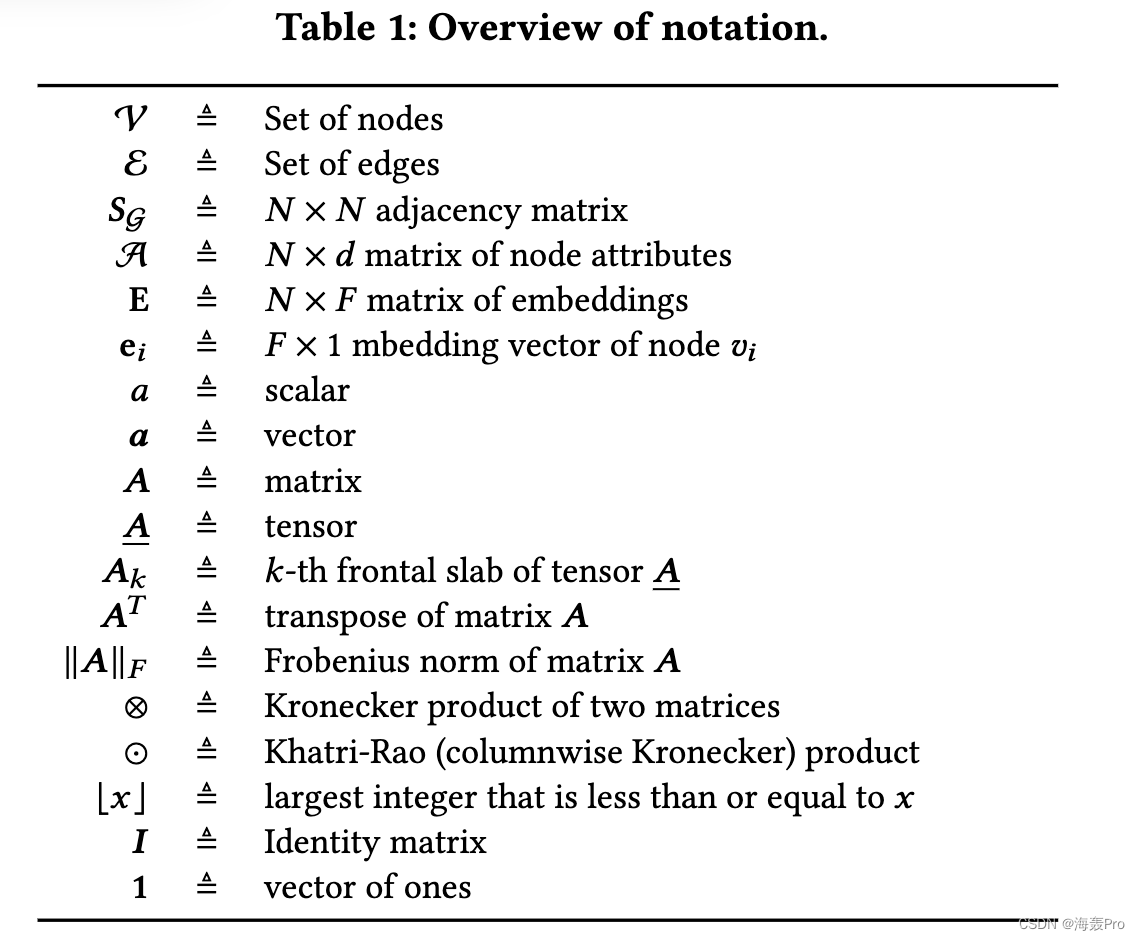
2 PRELIMINARIES

在进入论文的核心之前，我们简要讨论一些张量代数的预备知识，以方便阐述。读者可以参考 [23, 33] 了解更多关于张量的背景知识。

一个三阶张量𝑿∈R𝐼×𝐽×𝐾是三元素𝑿(𝑖,𝑗𝑘)。它包含三种模式——列𝑿(𝑖:𝑘):代表{1 , · · · , }结束,结束=𝐽这里),行𝑿(:,𝑗𝑘)和纤维𝑿(𝑖、𝑗:);和三种类型的板-水平𝑿(𝑖,:,:),垂直𝑿(:,𝑗:)和额𝑿(:,:,𝑘)。一个一阶张量𝒁∈R𝐼×𝐽×𝐾三个向量的外积,𝒂∈R𝐼𝒃∈R𝐽𝒄∈R𝐾,指示为𝒁=𝒂◦𝒃◦𝒄,◦外积算子。

任何三阶张量都可以分解为三路外积（一级张量）的总和，即

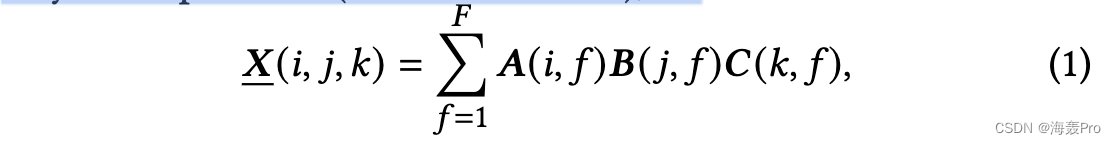
6 CONCLUSIONS

本文提出了一种新的基于张量的属性网络无监督节点嵌入方法GAGE

gag利用了多维缩放和标准多矢分解的有利特性，并提供了保留网络连接和属性的几何形状的嵌入

尽管所提出的方法适用于距离矩阵，而不是原始的邻接和属性，算法仍然可以利用图和属性的稀疏结构，并允许可伸缩和轻量级的实现

在真实世界的基准网络上的实验证明了所提出的GAGE在下游任务上的有效性

结语

文章仅作为个人学习笔记记录，记录从0到1的一个过程

希望对您有一点点帮助，如有错误欢迎小伙伴指正