进制转换、原码、反码、补码及位运算详解
目录
一、进制介绍
二进制是逢2进位的进位制,0、1是基本算符。
现代的电子计算机技术全部采用的是二进制,因为它只使用0、1两个数字符号,非常简单方便,易于用电子方式实现。计算机内部处理的信息,都是采用二进制数来表示的。二进制(Binary)数用0和1两个数字及其组合来表示任何数。进位规则是“逢2进1”,数字1在不同的位上代表不同的值,按从右至左的次序,这个值以二倍递增。
对于整数,有四种表示方式:
1、二进制:0,1.满2进1,以0b或0B开头。
2、十进制:0-9,满10进1。
3、八进制:0-7,满8进1,以数字0开头表示
4、十六进制:0-9及A(10)-F(15),满16进1,以0x或0X开头表示。此处的A-F不区分大小写。
二、二进制、八进制、十六进制转换为十进制
(1)二级制转换为十进制示例
规则:从最低位(右边)开始,将每个位上的数据提取出来,乘以2的(位数-1)次方,然后求和。
案例:将0b1011转为十进制的数
0b1011 = 1 * 2的(1-1)次方 + 1 * 2的(2-1)次方 + 0 * 2的(3-1)次方 + 1 * 2的(4-1)次方=
1 + 2 + 0 + 8 = 11
(2)八级制转换为十进制示例
规则:从最低位(右边)开始,将每个位上的数提取出来,乘以8的(位数-1),然后求和。
案例:将0234转为十进制的数
0234 = 4 * 8 ^ 0 + 3 * 8 ^ 1 + 2 * 8 ^ 2 = 4 + 24 + 128 = 156
(3)十六级制转换为十进制示例
规则:从最低位(右边)开始,将每个位上的数据取出来,乘以16的(位数-1)次方,然后求和。
案例:将0x23A转为十进制的数
0x23A = 10 * 16 ^ 0 + 3 * 16 ^ 1 + 2 * 16 ^ 2 = 10 + 48 + 512 = 570
三、十进制换行为二进制、八进制、十六进制
(1)十进制转换为二进制
规则:将该数不断除以2,直到商为0为止,然后将每步得到的余数倒过来,就是对应的二进制。
案例:将34转换为二进制 => 0B00100010 (不足一个字节8位,前面补两个0)
图解--
(2)十进制转换为八进制
规则:将该数不断除以8,直到商为0为止,然后将每步得到的余数倒过来,就是对应的二进制。
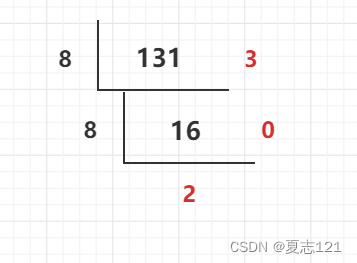
案例:将131转为八进制 => 0203
图解--
(3)十进制转换为十六进制
规则:将该数不断除以16,直到商为0为止,然后将每步得到的余数倒过来,就是对应的二进制。
案例:将237转为十六进制 => 0XED (14对应十六进制E,13对应十六进制D)
图解
四、二进制转换为八进制、十六进制
(1)二进制转换为八进制
规则:从低位开始,将二进制数每三位一组,转为对应的八进制即可。
案例:将0b11010101转为八进制
0b11(3)010(2)101(5)转为八进制 => 0325
(2)二进制转换为十六进制
规则:从低位开始,将二进制数每四位一组,转为对应的十六进制即可。
案例:将0b11010101转为十六进制
0b1101(13=>D)0101(5) = 0xD5
五、八进制、十六进制转换为二进制
(1)八进制转换为二进制
规则:将八进制数每1位,转为对应的一个3位的二进制数即可。
案例:将0237转成二进制
02(010)3(011)7(111) = 0b010011111
(2)十六进制转换为二进制
规则:将八进制数每1位,转为对应的一个4位的二进制数即可。
案例:将0x23B转为二进制
0x2(0010)3(0011)B(1011) = 0b001000111011
六、原码、反码、补码
1、二进制的最高位是符号位:0表示正数,1表示负数(口诀:0 => 0 1 => -)
2、正数的原码,反码,补码都一样(三码合一)
3、负数的反码=它的原码符号不变,其他位取反(0 => 1 1 => 0)
4、负数的补码 = 它的反码 + 1,负数的反码 = 负数的补码 - 1
5、0的反码,补码都是0
6、java没有无符号数,换而言之,java中的数都是有符号的
7、在计算机运算的时候,都是以补码的方式来运算的
8、当我们看运算结果的时候,要看他的原码(!!!)
七、位运算详解
java中有7个位运算(&、|、^、~、>>、<< 和 >>>)
分别是按位与&、按位或|、按位异或^、按位取反~,它们的运算规则是:
按位与&:两位全为1,结果为1,否则为0
按位或|:两位有一个为1,结果为1,否则为0
按位异或^:两位一个为0,一个为1,结果为1,否则为0
按位取反~:0 => 1,1 => 0
案例:
2&3
1、先得到2的补码 => 2的原码 00000000 00000000 00000000 00000010
2的补码 00000000 00000000 00000000 00000010(正数原码补码一样)
2、再得到3的补码 => 3的补码 00000000 00000000 00000000 00000011
3的补码 00000000 00000000 00000000 00000011(正数原码补码一样)
3、按位&
00000000 00000000 00000000 00000010
00000000 00000000 00000000 00000011
00000000 00000000 00000000 00000010 & 运算后的补码
运算后的原码也是 00000000 00000000 00000000 00000010
结果就是 2
~ -2
1、先得到-2的原码 1000000 00000000 00000000 00000010
2、-2的反码 11111111 11111111 11111111 11111101
3、-2的补码 11111111 11111111 11111111 11111110
4、~ -2 操作 0000000 00000000 00000000 0000001 运算后的补码
5、运算后的原码 就是 0000000 00000000 00000000 0000001 => 1
~ 2
1、得到2的补码 0000000 00000000 00000000 00000010 (正数原码和补码一样得出)
2、~ 2操作 11111111 11111111 11111111 11111101 运算后的补码
3、运算后的反码 11111111 11111111 11111111 11111100 (负数补码为-1)
4、运算后的原码 10000000 00000000 00000000 00000011 (负数反码符号不变,其他取反得出) => -3
还有3个位运算符>>、<< 和 >>>,运算规则:
1、算术右移>>:低位溢出,符号位不变,并用符号位补溢出的高位
2、算术左移<<:符号位不变,低位补0
3、>>> 逻辑右移也叫无符号右移,运算规则:低位溢出,高位补0
4、特别说明:没有 <<< 无符号
案例:
int a = 1 >> 2;//1=> 00000001 => 00000000 本质1 / 2 / 2 = 0
int c = 1 << 2; //1=> 00000001 => 00000100本质1 * 2 * 2 = 4
- 点赞
- 收藏
- 关注作者


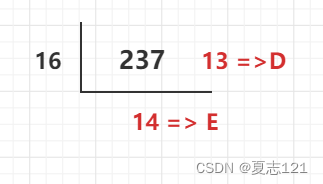

评论(0)