@TOC

简介

Hello！
非常感谢您阅读海轰的文章，倘若文中有错误的地方，欢迎您指出～
 
ଘ(੭ˊᵕˋ)੭
昵称：海轰
标签：程序猿｜C++选手｜学生
简介：因C语言结识编程，随后转入计算机专业，获得过国家奖学金，有幸在竞赛中拿过一些国奖、省奖…已保研
学习经验：扎实基础 + 多做笔记 + 多敲代码 + 多思考 + 学好英语！
 
唯有努力💪
 
【每日一读】每天浅读一篇论文，了解专业前沿知识，培养阅读习惯（阅读记录 仅供参考）

论文简介

原文链接：https://dl.acm.org/doi/10.1145/3488560.3498383

会议：WSDM '22: Proceedings of the Fifteenth ACM International Conference on Web Search and Data Mining （CCF B类）

年度：2022年2月15日

ABSTRACT

随机节点采样是大规模网络分析中的基本算法原语，许多现代图挖掘算法都严重依赖它

我们考虑在网络中生成大量随机节点的任务，假设查询访问受限（查询节点会显示其邻居集）

在当前的方法中，基于长随机游走，每个样本的查询数量与网络的混合时间成线性比例，这对于大型现实世界网络来说可能是令人望而却步的

我们提出了一种采样多个节点的新方法，该方法通过显式搜索网络中不易访问的组件来绕过混合时间的依赖性

我们在具有多达数千万个节点的各种现实世界和合成网络上测试了我们的方法，与现有技术相比，查询复杂度提高了 20 倍

1 INTRODUCTION

二十多年来，根据规定分布对节点进行随机抽样已广泛用于现代大型网络的分析[22, 32]

鉴于现代网络的巨大规模，以及它们通常可以通过节点（或边缘）查询访问的事实，随机节点采样提供了最自然的方法，有时甚至是唯一的方法，可以快速准确地解决网络分析任务

其中包括，例如，阶数估计 [29]、平均度数和度数分布 [11、15、59]、三角形数 [2]、聚类系数 [51] 和中介中心性 [7]，等等其他
此外，节点采样是许多标准网络算法用于快速探索网络的基本原语，例如，用于检测频繁的子图模式 [42] 或社区 [44, 57]，或用于减轻不希望的情况的影响，例如传送在 PageRank [ 21 ] 中

因此，近期大量研究致力于在大型社会和信息网络中生成随机节点的效率。参见例如 [8, 9, 26, 39, 41, 46, 60] 和其中的参考文献。

---

问题表述

我们考虑实现一个采样预言机的任务，该预言机允许一个人根据规定的分布（例如，均匀分布）对网络中的多个节点进行采样

采样节点的集合应该是独立同分布的

随机节点采样的标准算法假设查询访问网络的节点，其中查询节点会显示其邻居

作为起点，我们可以从网络访问单个节点，我们的目标是使用少量查询从所需分布中生成一组（可能很大）样本

一个典型的效率度量是摊销查询复杂度——节点查询的总数除以采样节点的数量

这扩展了 Chierichetti 等人提出的框架。 [8, 9]，他研究了对单个节点进行采样的查询复杂度

为简单起见，我们专注于均匀分布的重要情况，但我们的方法可以很容易地推广到任何自然分布

我们考虑所需的节点样本数N很大

---

随机游走及其局限性

以前关于节点采样的大多数工作都集中在基于随机游走的方法上，它自然地利用节点查询访问网络

它们用途广泛，可实现卓越的效率 [8, 10, 26, 39]

随机游走从种子节点开始，然后从当前节点继续到随机邻居，直到它（几乎）收敛到其平稳分布

然后，根据游走的平稳分布选择一个随机节点，如果它与期望的不同，可以适当修改[8]

随机游走（几乎）收敛到平稳分布之前的步数称为混合时间，通常用 $𝑡_{mix}$ 表示

基于 RW 的方法在具有良好扩展特性的高度连接网络中非常有效，其中混合时间是对数的 [25]

然而，在大多数现实世界的网络中，情况要复杂得多

到目前为止，众所周知的现象是，许多现实世界的社交网络中的混合时间大约为数百甚至数千，远高于理想化的扩展网络 [13, 40, 43]

作为这项工作的一部分，我们证明了对多个节点进行采样的下限：在网络结构的标准假设下，使用随机游走对𝑁（几乎）均匀且不相关的随机节点的集合进行采样可能需要 $Ω(𝑁 · 𝑡_{mix})$ 查询

鉴于 $𝑡_{mix}$中的乘法依赖，随着𝑁变大，这个界限变得令人望而却步

1.1 Our Contribution

根据以上讨论，我们提出以下问题：我们能否设计一种查询效率高的方法来对大量节点进行采样，而不是乘法地依赖于网络的混合时间？

我们通过提出一种用于采样节点的新算法来肯定地回答这个问题，其查询复杂度比最先进的随机游走算法小 20 倍

• 据我们所知，这是第一个不基于长随机游走的节点采样方法

随机游走的下限

• 我们提出了一个 $Ω(𝑁 · 𝑡_{mix})$ 下界，用于使用朴素随机游走（不尝试学习网络结构）从网络中采样 𝑁 均匀且独立的节点
• 我们的下界结构是一个图，由一个类似扩展器的大部分和许多通过桥连接到它的小组件组成，这种结构在大型社交网络中非常常见 [38]
• 主要的直觉是，从网络中采样𝑁节点需要步行访问许多小社区，从而跨越 Θ(𝑁 ) 桥，预计每个桥需要 $Θ(𝑡_{mix})$ 查询，总共需要 $Θ(𝑁 · 𝑡_{mix})$

绕过乘法依赖

• 我们提出了一种用于对多个节点进行采样的新算法 SampLayer，其查询复杂度不会乘法地依赖于混合时间
• 我们的算法将网络结构分解为一个高度连接的部分和许多小的外围组件
• 我们还展示了我们算法的一个更强大的变体 SampLayer+，它在更具表现力的查询模型中工作，其中查询一个节点还可以揭示其邻居的度数（而不仅仅是标识符）

我们的方法受到核心-外围的启发对社交网络的看法 [48]

• 首先使用偏向更高阶节点的随机游走来探索图
• 有了高度节点，我们构建了一个数据结构，将这些节点的所有非邻居划分为非常小的组件
• 然后，我们使用数据结构快速到达这些组件（并随后从中采样）；该过程涉及在到达的组件内运行 BFS，由于它的体积很小，不需要很多查询

我们从理论上将 SampLayer 的查询复杂性与几个网络参数联系起来，并表明它们在实践中表现良好

我们的算法生成的样本可以证明是独立的并且几乎是均匀的

---

改进的经验表现

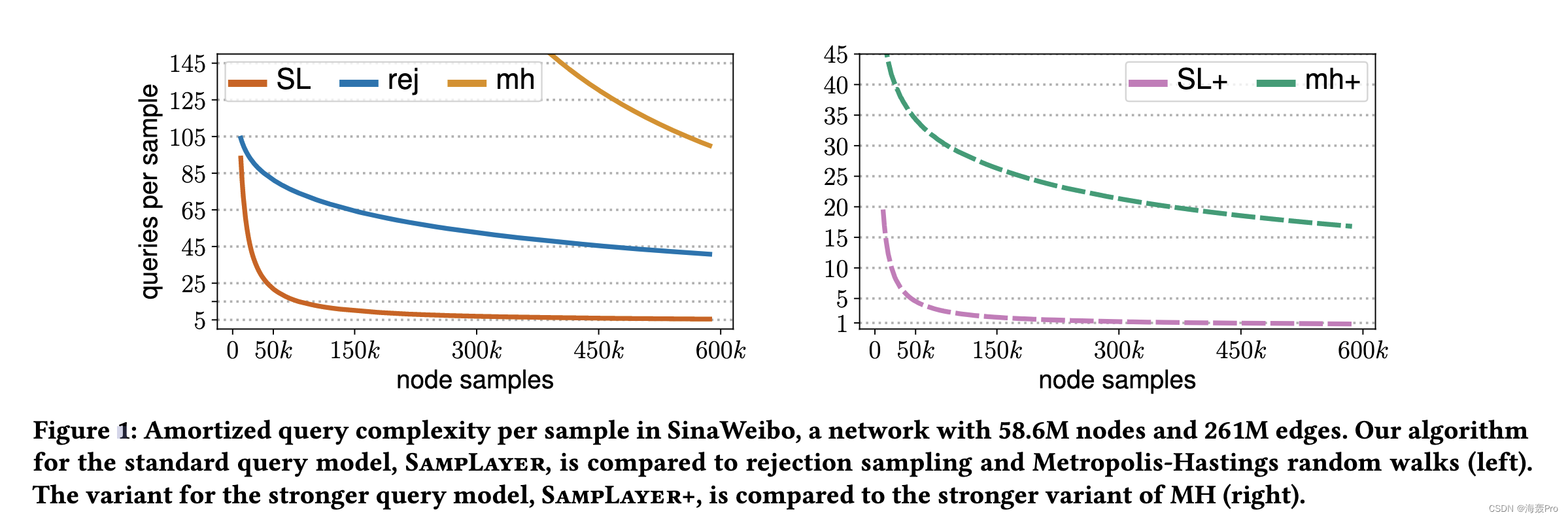
我们将 SampLayer 的摊销查询复杂度与节点采样、拒绝采样 (REJ) 和 Metropolis-Hastings (MH) 方法的两种最具代表性和标准的基于随机游走的方法进行比较； SampLayer+ 与 MH+ 进行比较，MH+ 是程度揭示模型中 MH 的类似物。有关 REJ、MH 和 MH+ 的完整描述以及对其查询复杂性的理论和实证分析，请参阅 Chierichetti 等人的工作。 [8]。我们对七个具有不同特征的现实世界社交和信息网络进行了比较，其中最大的是新浪微博[58]，它由超过 50M 的节点和 250M 的边组成。 图 1 和图 8 以及第 4.1 节中显示的结果表明，当 𝑁 不是非常小时，我们算法的查询复杂度明显优于基于随机游走的算法。 这既适用于标准查询模型（即 SampLayer 与 REJ 和 MH），也适用于更强的显示度数查询模型（SampLayer+ 与 MH+）。 在这两种模型中，对于所有七个网络，我们都将查询复杂性降低了至少 40% 和最多 95%。 值得注意的是，如图 1 所示，在某些情况下，即使 𝑁 小于网络大小的 1%，SampLayer 也可以实现每个样本低至 5 个查询的接近最优查询复杂度。 在 SampLayer+ 中，这更加引人注目，基本上实现了每个样本一个查询。

生成模型

对我们的发现的一种可能解释可能在于 Leskovec 等人的开创性工作。 [38]。在对大型现实世界社交和信息网络中的社区结构进行的最广泛分析之一中，他们检查了各个领域的 100 多个大型网络。他们发现当时的大多数经典生成模型都没有很好地捕捉社区结构和社交网络的其他各种属性（例如，社区的规模、它们与图的连接性、随时间的缩放等）。森林火灾生成模型 [36, 37] 的开发是为了填补这一空白，更符合实证研究结果。在这个现在已经成为标准且经过充分研究的模型中，添加边缘的方式会产生小的、几乎没有连接的片段，这些片段比随机的要大得多且密集得多。我们展示了我们的算法在此模型生成的网络上表现非常好（查询复杂度持续提高了 30-50%），即使对于微小的核心大小也是如此；见图 2。

1.2 Related Work

在过去的十年中，基于随机游走的节点采样方法得到了广泛的研究。 Chierichetti 等人的上述工作。 [8] 是最接近我们的，研究这种方法的查询复杂性。 Iwasaki 和 Shudo [26] 的分析还侧重于随机游走的平均查询复杂度。

使用随机节点抽样来确定大规模网络的属性可以追溯到 Leskovec 和 Faloutsos [34] 的开创性工作。从那时起，通过随机游走进行节点采样的性能在网络参数估计的背景下得到了广泛的考虑。例如，Katzir 等人。 [28, 29] 使用随机游走来估计网络顺序和基于采样和碰撞计数的聚类系数。库珀等人。 [10] 提出了一个基于随机游走的通用框架，用于估计各种网络参数；而里贝罗等人。 [46] 将这些方法扩展到有向网络。 Ribeiro 和 Towsley [45] 使用多维随机游走。伊甸园等人。 [ 16 – 18 ] 以及 Tětek 和 Thorup [ 55 ] 研究了在访问统一节点的情况下生成统一边的查询复杂性。 Bera 和 Seshadhri [5] 设计了一种精确的亚线性三角形计数算法，它只查询一小部分图边。有关网络估计工作的其他几个示例，请参阅 [20, 27, 30, 39, 41, 60]。

在许多这些工作中，通过放宽对独立样本的要求来提高查询复杂性。然而，了解采样节点之间的依赖关系如何影响结果，本质上需要针对所讨论的网络参数进行复杂的分析。我们的方法生成的节点不需要这样的分析，这些节点可以证明是独立的。从技术角度来看，我们对网络隔离组件的自适应探索与通过确定性探索 [50] 进行的节点采样和用于网络完成的节点探测方法（例如 [6, 33, 52, 53]）有一些相似之处 [24, 31 ]。鉴于访问网络的不完整副本，Soundarajan 等人。 [52, 53] 和 LaRock 等人。 [33] 通过自适应网络探索发现未观察到的部分；参见 Eliassi-Rad 等人的调查。 [19]。

将网络的核心-外围特征用于算法目的却很少受到关注。 最相关的工作是 Benson 和 Kleinberg [4] 关于链接预测的工作。 更弱相关的是社交网络的 𝑘-cores [1, 14] 的研究，其旨在通过迭代删除小度节点来捕获所有“参与”节点的子集。

2 LOWER BOUND FOR RANDOM WALKS

在本节中，我们快速介绍了使用随机游走对 𝑁（几乎）独立且均匀分布的节点进行采样所需的查询数量的 Ω(𝑁 · 𝑡mix) 下限。 请参阅完整版 [3] 中的证明草图。 为清楚起见，我们将分析重点放在最标准的随机游走上，它在任何给定时间从当前节点到其邻居之一，均匀随机； 这种随机游走用于拒绝抽样（REJ）。 类似的下界也适用于其他不学习网络结构特征的随机游走变体，包括 MH 和 MH+。

定理 2.1。 对于任何 𝑛 和 log 𝑛 ≪ 𝑡 ≪ 𝑛Θ(1) ，在 𝑛 顶点上存在一个图 𝐺，混合时间为 𝑡mix = Θ(𝑡)，满足以下条件：对于任何 𝑁 ≤ 𝑛Θ(1) ，任何基于采样算法 在输出（几乎）一致的𝑁节点集合的均匀随机游走上，必须执行 Ω(𝑁 · 𝑡mix) 查询。

3 ALGORITHM

5 CONCLUSIONS AND OPEN QUESTIONS

我们提出了一种算法，该算法支持对大型社交网络中的多个节点进行高效查询采样，在包括多达数千万个节点的各种数据集上展示了我们的算法与现有技术相比的效率

我们根据几个图形参数给出了算法复杂性的理论界限

然后，我们凭经验证实，在我们检查过的所有社交网络中，这些图参数表现良好

一个主要问题是普遍性问题。也就是说，我们的方法适用的网络范围是什么

如实验部分所述，我们的算法在我们测试过的所有社交网络上都给出了更好或可比较的结果，并且在 Forest Fire 模型（一种现实的生成模型）上的良好性能进一步暗示了广泛的适用性

---

与随机游走相比，我们的算法有一些缺点

• 首先，它要复杂得多，它的分析不直接依赖于网络的一个结构参数（例如随机游走的混合时间）
• 其次，它本质上依赖于具有高内存消耗的数据结构，并且可能并不总是适用于需要有限内存算法的情况
• 第三，它取决于𝐿0的大小，不同网络之间的大小不同，因此需要根据给定的网络进行微调
• 最后，它利用了社交网络的独特属性。 这些属性不适用于有界度图或现实世界的道路网络。 对于这样的图，我们期望我们的算法比随机游走表现更差。

说了这么多，我们的工作表明，在各种真实和合成的社交网络中，可以使用结构分解和仔细的预处理来显着节省查询复杂性

我们不认为我们的算法应该取代基于 RW 的方法

事实上，这些算法是节点采样的黄金标准，并在网络分析中提供了一个非常通用的原语

相反，当需要多个节点样本并且所讨论的网络具有合适的社区结构时，可以将我们的算法视为有用的替代方案

进一步探索将我们方法的查询效率与随机游走的灵活性相结合的方法将是非常有趣的

例如，我们的基于核心-外围的数据结构如何用于加速重要网络参数的计算，或者社区结构的检测？

结语

文章仅作为个人学习笔记记录，记录从0到1的一个过程

希望对您有一点点帮助，如有错误欢迎小伙伴指正