简介

Hello！
非常感谢您阅读海轰的文章，倘若文中有错误的地方，欢迎您指出～
 
ଘ(੭ˊᵕˋ)੭
昵称：海轰
标签：程序猿｜C++选手｜学生
简介：因C语言结识编程，随后转入计算机专业，获得过国家奖学金，有幸在竞赛中拿过一些国奖、省奖…已保研
学习经验：扎实基础 + 多做笔记 + 多敲代码 + 多思考 + 学好英语！
 
唯有努力💪
 
【每日一读】每天浅读一篇论文，了解专业前沿知识，培养阅读习惯（阅读记录 仅供参考）

论文简介

原文链接：https://dl.acm.org/doi/10.1145/3394486.3403065

会议：KDD '20: Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining （CCF A类）

代码：https://github.com/ChandlerBang/Pro-GNN

年度：2020年8月20日

ABSTRACT

注意力运算符已应用于文本等一维数据和图像和视频等高阶数据

在高阶数据上使用注意算子需要将空间或时空维度展平为一个向量，假设该向量遵循多元正态分布

这不仅会对计算资源产生过多的要求，而且无法保留数据中的结构

在这项工作中，我们建议通过假设数据遵循矩阵变量正态分布来避免扁平化

基于这种新观点，我们开发了直接对高阶张量数据进行操作的 Kronecker 注意算子 (KAO)

更重要的是，提议的 KAO 导致计算资源的显着减少

实验结果表明

• 我们的方法将所需的计算资源量减少了数百倍，对于高维和高阶数据的因子更大
• 具有 KAO 的网络优于没有注意力的模型，同时实现了与具有原始注意力算子的网络竞争的性能

1 INTRODUCTION

具有注意算子的深度神经网络在解决自然语言处理 [3, 19, 33]、计算机视觉 [26, 38] 和网络嵌入 [9, 34] 等各个领域的挑战性任务方面表现出强大的能力

注意力算子能够捕获远程依赖关系，从而显着提升性能[23、27]

虽然注意力算子最初是针对一维数据提出的，但最近的研究 [7, 35, 40] 试图将它们应用于高阶数据，例如图像和视频

然而，在高阶数据上使用注意力算子的一个实际挑战是对计算资源的过度要求，包括计算成本和内存使用

例如，对于二维图像任务，时间和空间复杂度都是输入特征图的高度和宽度乘积的二次方

随着空间或时空维度和输入数据顺序的增加，这个瓶颈变得越来越严重

先前的方法通过在注意力运算符 [35] 之前对数据进行下采样或限制注意力路径 [16] 来解决这个问题

在这项工作中，我们为高阶数据提出了新颖且高效的注意力算子，称为 Kronecker 注意力算子 (KAO)

我们从概率的角度研究上述问题，具体来说，常规注意力操作符将数据展平，并假设展平的数据遵循多元正态分布

这种假设不仅导致高计算成本和内存使用，而且无法保留数据的空间或时空结构

相反，我们建议使用矩阵变量正态分布对数据进行建模，其中 Kronecker 协方差结构能够捕捉空间或时空维度之间的关系

基于这种新观点，我们提出了我们的 KAO，它避免了扁平化并直接对高阶数据进行操作

实验结果表明，KAO 与原始注意力算子一样有效，同时大大减少了所需的计算资源量

特别是，我们使用 KAO 来设计一系列高效模块，从而产生了我们称为 Kronecker 注意力网络 (KANets) 的紧凑型深度模型

• KANets 在图像分类任务上显着优于先前的紧凑模型，参数更少，计算成本更低
• 此外，我们对图像分割任务进行了实验，以证明我们的方法在一般应用场景中的有效性

2 BACKGROUND AND RELATED WORK

在本节中，我们将描述注意力和相关的非局部算子，它们已应用于文本、图像和视频等各种类型的数据

2.1 Attention Operator

注意算子的输入包括一个查询矩阵 Q =(︀q 1, q2,⋯, qm ⌋︀ ∈ Rd×m，每个 qi ∈ Rd ，一个关键矩阵 K =(︀k 1, k2, ⋯, kn ⌋︀ ∈ Rd×n 与每个 ki ∈ Rd 和一个值矩阵 V = (︀ v 1, v2,⋯, vn ⌋︀ ∈ Rp×n 与每个 vi ∈ Rp

注意力操作通过参与计算查询向量 qi 的响应到 K 中的所有关键向量，并使用结果对 V 中的值向量进行加权求和

注意算子的逐层前向传播操作可以表示为

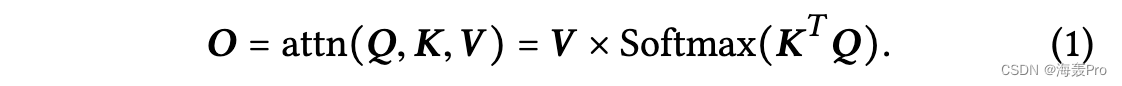
KT 和 Q 之间的矩阵相乘得到系数矩阵 E = KT Q，其中每个元素 ei j 由 kT i 和 qj 之间的内积计算。该系数矩阵 E 计算每个查询向量 qi 和每个关键向量 kj 之间的相似度得分，并通过按列的 softmax 算子进行归一化，以使每列总和为 1。输出 O ∈ Rp×m 是通过将 V 与归一化的E. 在自注意力运算符 [33] 中，我们有 Q = K = V。图 1 提供了注意力操作符的说明。等式中的计算成本。 1 是 O(m ×n × (d +p))。存储中间系数矩阵E所需的内存为O(mn)。如果 d = p 和 m = n，则时间和空间复杂度分别变为 O(m2 × d) 和 O(m2)。

还有其他几种从 Q 和 K 计算 E 的方法，包括高斯函数、点积、级联和嵌入式高斯函数。已经表明，点积是最简单但最有效的一种 [35]。因此，我们在这项工作中关注点积相似度函数。

在实践中，我们可以首先对每个输入矩阵进行单独的线性变换，得到以下注意算子：O = W V V Softmax((W K K)T W Q Q)，其中 W V ∈ Rp′×p ， W K ∈Rd′×d ， W Q ∈ Rd′×d 。为了符号简单，我们在下面的讨论中省略了线性变换。

注意力机制的介绍

2.2 Non-Local Operator

[35] 中提出的非局部算子将自注意力算子应用于图像和视频等高阶数据

以二维数据为例，非局部算子的输入是一个三阶张量 X ∈ Rh×w ×c ，其中 h、w 和 c 分别表示通道的高度、宽度和数量.

张量首先通过沿模式 3 [ 21 ] 展开转换为矩阵 X (3) ∈ Rc×hw，如图 2 所示

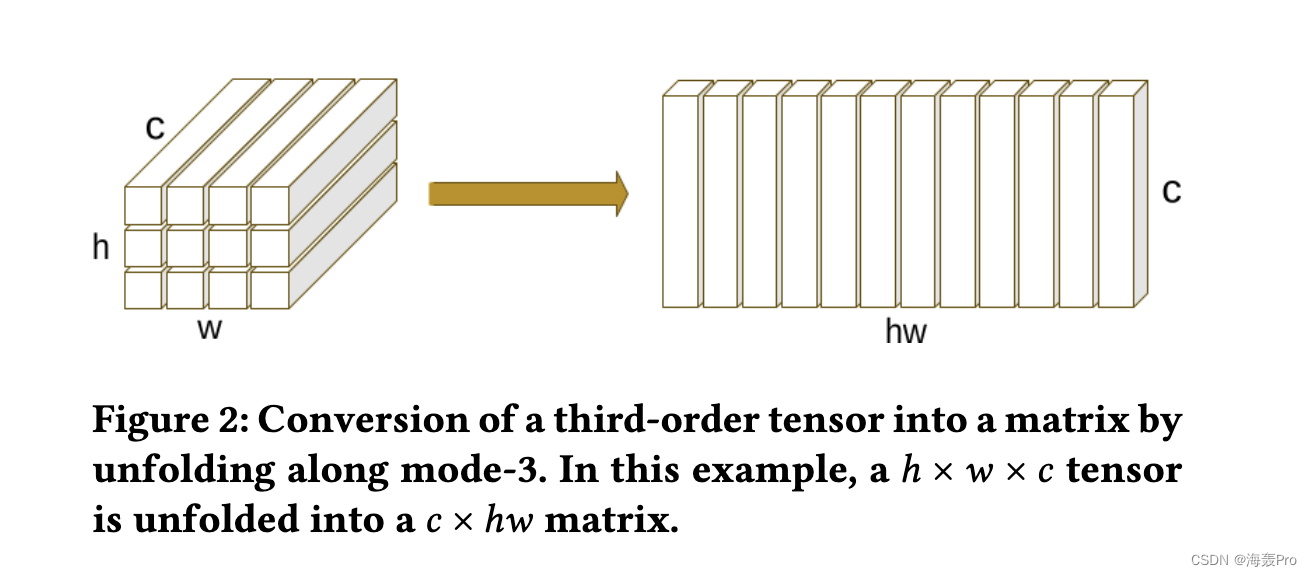
然后我们执行方程式中的操作。 1 通过设置 Q = K = V = X (3)。注意算子的输出被转换回三阶张量作为最终输出。

非本地算子的一个实际挑战是它消耗过多的计算资源

• 如果 h = w，则二维非局部算子的计算成本为 O(h4 × c)
• 用于存储中间系数矩阵的内存会产生 O(h4) 空间复杂度
• 高维和高阶数据的时间和空间复杂度高得令人望而却步

3 KRONECKER ATTENTION NETWORKS

在本节中，我们描述了我们提出的 Kronecker 注意算子，它们是高阶数据上高效且有效的注意算子

我们还描述了如何使用这些算子来构建 Kronecker 注意力网络

…

5 CONCLUSIONS

在这项工作中，我们提出了 Kronecker 注意算子来解决在高阶数据上应用注意算子的实际挑战

我们从概率的角度研究这个问题，并使用具有 Kronecker 协方差结构的矩阵变量正态分布

实验结果表明

• 我们的 KAO 将所需的计算资源量减少了数百倍
• 对于更高维和更高阶的数据具有更大的因子，我们使用 KAO 来设计一系列高效模块，从而产生了我们的 KANet

KANets 在图像分类任务上显着优于之前最先进的紧凑模型，参数更少，计算成本更低

此外，我们对图像分割任务进行了实验，以展示我们的 KAO 在一般应用场景中的有效性

读后总结

针对高阶数据的注意力计算算子

目前还用不到 哈哈 大概率是低阶的

结语

文章仅作为个人学习笔记记录，记录从0到1的一个过程

希望对您有一点点帮助，如有错误欢迎小伙伴指正

文章来源: haihong.blog.csdn.net，作者：海轰Pro，版权归原作者所有，如需转载，请联系作者。

原文链接：haihong.blog.csdn.net/article/details/127048040