【数学建模】线性规划
【摘要】 司守奎 《数学建模算法与应用》 第二版线性规划问题是在一组线性约束条件的限制下,求一线性目标函数最大或最小的问题。问题的约束条件记为s.t.(即subject to)。由于上面的目标函数及约束条件均为线性函数,故称为线性规划问题。 matlab求解线性规划问题matlab规定线性规划的标准形式式中:f,x,b,beq,lb,ub为列向量,其中f称为价值向量,b称为资源向量;A,Aeq为矩阵。...
司守奎 《数学建模算法与应用》 第二版
线性规划问题是在一组线性约束条件的限制下,求一线性目标函数最大或最小的问题。

问题的约束条件记为s.t.(即subject to)。
由于上面的目标函数及约束条件均为线性函数,故称为线性规划问题。
matlab求解线性规划问题
matlab规定线性规划的标准形式
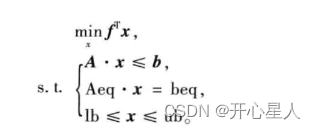
式中:f,x,b,beq,lb,ub为列向量,其中f称为价值向量,b称为资源向量;A,Aeq为矩阵。
Matlab中求解线性规划的命令为
[x,fval]linprog(f,A,b)
[x,fval]linprog(f,A,b,Aeq,beq)
[x,fval]linprog(f,A,b,Aeq,beq,lb,ub)
式中:x返回决策向量的取值;fval返回目标函数的最优值;f为价值向量;A和b对应线性不等式约束;Aeq和beq对应线性等式约束;lb和ub分别对应决策向量的下界向量和上界向量。
转换为标准形式
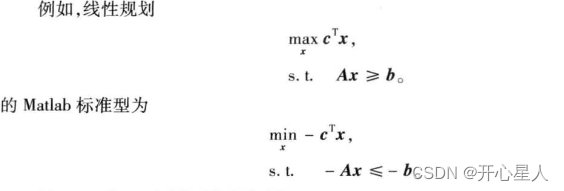
例题
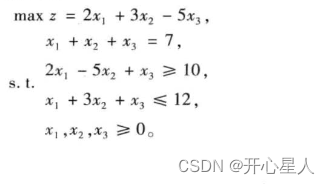
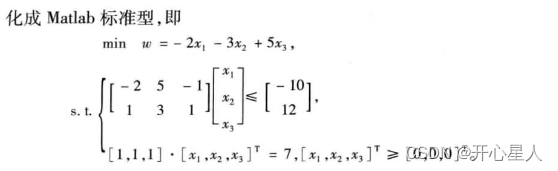
clc,clear;
f = [2; 3; -5];
a = [-2 5 -1; 1 3 1];
b = [-10; 12];
aeq = [1 1 1];
beq = 7;
lb = zeros(3, 1);
%//f取-f意为取反的最小值
[x, fval] = linprog(-f, a, b, aeq, beq, lb);
fprintf('x1=%.4f, x2=%.4f, x3=%.4f\nz=%.4f\n', x, -fval);
可以转换成线性规划的问题



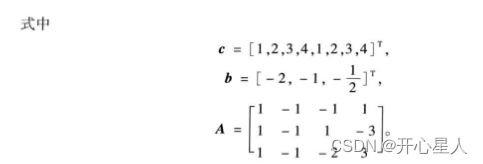

多目标规划问题

1)确定一个最大的风险率,所以可以将风险率放到约束条件中去了,而不是作为目标函数

2)确定一个最小的收益,所以可以将收益放到约束条件中去了,而不是作为目标函数

3)对不同的目标附上权重

【声明】本内容来自华为云开发者社区博主,不代表华为云及华为云开发者社区的观点和立场。转载时必须标注文章的来源(华为云社区)、文章链接、文章作者等基本信息,否则作者和本社区有权追究责任。如果您发现本社区中有涉嫌抄袭的内容,欢迎发送邮件进行举报,并提供相关证据,一经查实,本社区将立刻删除涉嫌侵权内容,举报邮箱:
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者


评论(0)