目录

前言

本文摘自以下文献，为个人学习笔记摘抄：

• 《多方安全计算研究综述》 —— 蒋凯元

百万富翁问题

1980 年代，姚期智院士提出了经典的 “百万富翁” 难题：两个百万富翁街头邂逅，他们都想炫一下富，比比谁更有钱。但是出于隐私，双方都不想让对方知道自己到底拥有多少财富。如何在不借助第三方的情况下，让两位富翁知道他们之间谁更有钱？

一个经典解决方案为：假设这两个富翁为张三、李四，拥有资产分别为：张三拥有 300 万，李四拥有 500 万。

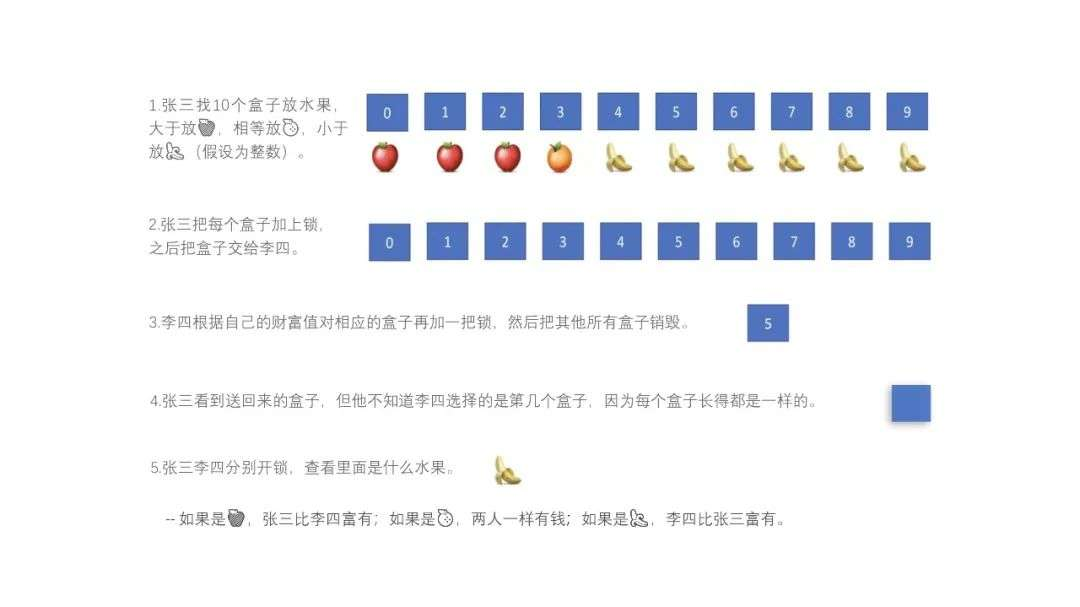
以上案例中，李四选了财富值对应的盒子并销毁了其他盒子，张三打开 “盲盒” 看到香蕉就可以明白，李四比自己更富有。双方在没有暴露自身资产金额的情况下，比较出了谁更富有。

多方安全计算

百万富翁难题在专业学者眼里，这其实是一个密码学的问题，可以表述为 “一组互不信任的参与方在需要保护隐私信息以及没有可信第三方的前提下进行协同计算的问题”，也被称为多方安全计算（Security Multi-Party Computation，简称 MPC，亦可简称 SMC 或 SMPC）。

MPC 可以保障多个参与方进行协同计算并输出计算结果的同时，使各个参与方除了计算结果之外无法获取任何其他信息，从技术层面实现数据的可用不可见。

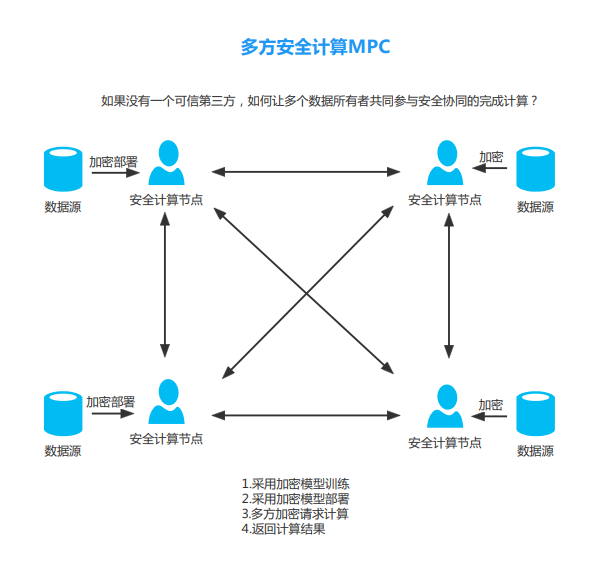
MPC 的数学定义为：假设存在ｎ 个参与方 P1,P2,…,Pn，每个参与方都有一个私有输入数据 xi，所有参与方共同计算某个函数 f(x1, x2, …, xn)，且要求在计算结束时，每个参与方 Pi 只能得到私有输入数据 xi 的输出，而不能获取其他参与方的输入信息及输出结果信息。

MPC 根据参与方数量的不同，可分为：两方计算（two party computation，简称 2PC）和多方计算（multi-party computation），这两者间存在本质的区别。

目前，通用的两方计算（2PC）已经具备了商用的条件。多方计算在某些特定场景下也已经没有太多的性能瓶颈；而通用计算协议在可扩展性层面依然不够成熟，这也是学术界一直在探索的方向。

在技术标准方面，中国通信标准化协会（CCSA）制定了：

• 《基于多方安全计算的数据流通产品技术要求与测试方法》
• 《隐私计算多方安全计算产品性能要求与测试方法》
• 《隐私计算 多方安全计算安全要求与测试方法》
• 等标准。

MPC 的发展历程

• 1978 Rivest 首次提出同态加密这一概念。

• 1979 Shamir 提出门限秘密分享协议。

• 1981 Rabin 提出不经意传输协议。

• 1982 Yao 提出多方安全计算协议（解决百万富翁问题）。

• 1986 Yao 提出混淆电路。

• 1987 Goldreich 提出基于秘密分享的 MPC。

• 1995 Chor 提出 PIR 协议。

• 1999 Paillier 提出半同态加密协议。

• 2004 Freedman 提出 PSI 协议。

• 2004 Malkhi 提出了一个名为 Fairplay 的多方安全计算平台。

• 2009 Gentry 提出全同态加密协议。

• 2009 Bogetoft 应用于丹麦甜菜拍卖。

• 2010 Burkhart 应用于隐私保护网络安全监控。

• 2016 Doerner 应用于隐私保护稳定匹配。

• 2017 Bestavros 应用于波士顿工资平等研究。

• 2018 年 3 月，Google 开源基于 TensorFlow 的 MPC 框架（https://github.com/tf-encrypted/tf-encrypted）。

• 2019 年 6 月，Google 开源 MPC 工具 Private Join and Compute（https://github.com/Google/private-join-and-compute）。

• 2019 年 10 月，Facebook 开源 MPC 框架 CrypTen（https://github.com/facebookresearch/CrypTen）。

MPC 的适用场景

数据可信交换

MPC 理论为不同机构见提供了一套构建在协同计算网络中的信息索引、查询、交换和数据跟踪的统一标准，可实现机构间数据的可信互联互通，解决数据安全性、隐私性问题，大幅降低数据信息交易抹茶和交易成本，为数据拥有方和需求方提供有效的对接渠道，形成互惠互利的交互服务网络。

数据安全查询

数据安全查询问题是 MPC 的重要应用领域。使用 MPC 技术，能保证数据查询方仅得到查询结果，但对数据库其他记录信息不可知。同时，拥有数据库的一方，不知道用户具体的查询请求。

联合数据分析

随着多数据技术的发展，社会活动中产生和搜集的数据和信息量急剧增加，敏感信息数据的收集、跨机构的合作以及跨国公司的经营运作等给传统数据分析算法提出了新的挑战，已有的数据分析算法可能会导致隐私暴露，数据分析中的隐私和安全性问题得到了极大的关注。

将 MPC 技术引入传统的数据分析领域，能够一定程度上解决该问题，其主要目的是改进已有的数据分析算法，通过多方数据源协同分析计算，使得敏感数据不被泄露。

MPC 的逻辑架构

安全多方计算主要分为 2 个参与方：

1. 枢纽节点：不参与实际协同计算，主要用于控制传输网络、路由寻址及计算逻辑传输。
2. 参与（MPC）节点：各个参与节点地位相同，可以发起协同计算任务，也可以选择参与其他方发起的计算任务。

此外，在去中心化的网络拓扑里，枢纽节点是可以删减的，参与节点可以与其他参与节点进行点到点连接，直接完成协同计算。

每个数据持有方可发起协同计算任务，并通过枢纽节点进行路由寻址，选择相似数据类型的其余数据持有方进行安全的协同计算。参与协同计算的多个数据持有方的参与节点会根据计算逻辑，从本地数据库中查询所需数据，共同就安全多方计算任务在密态数据流间进行协同计算。整个过程各方的明文数据全部在本地存储，并不会提供给其他节点。在保证数据隐私的情况下，枢纽节点将计算结果输出至整个计算任务系统，从而各方得到正确的数据结果。

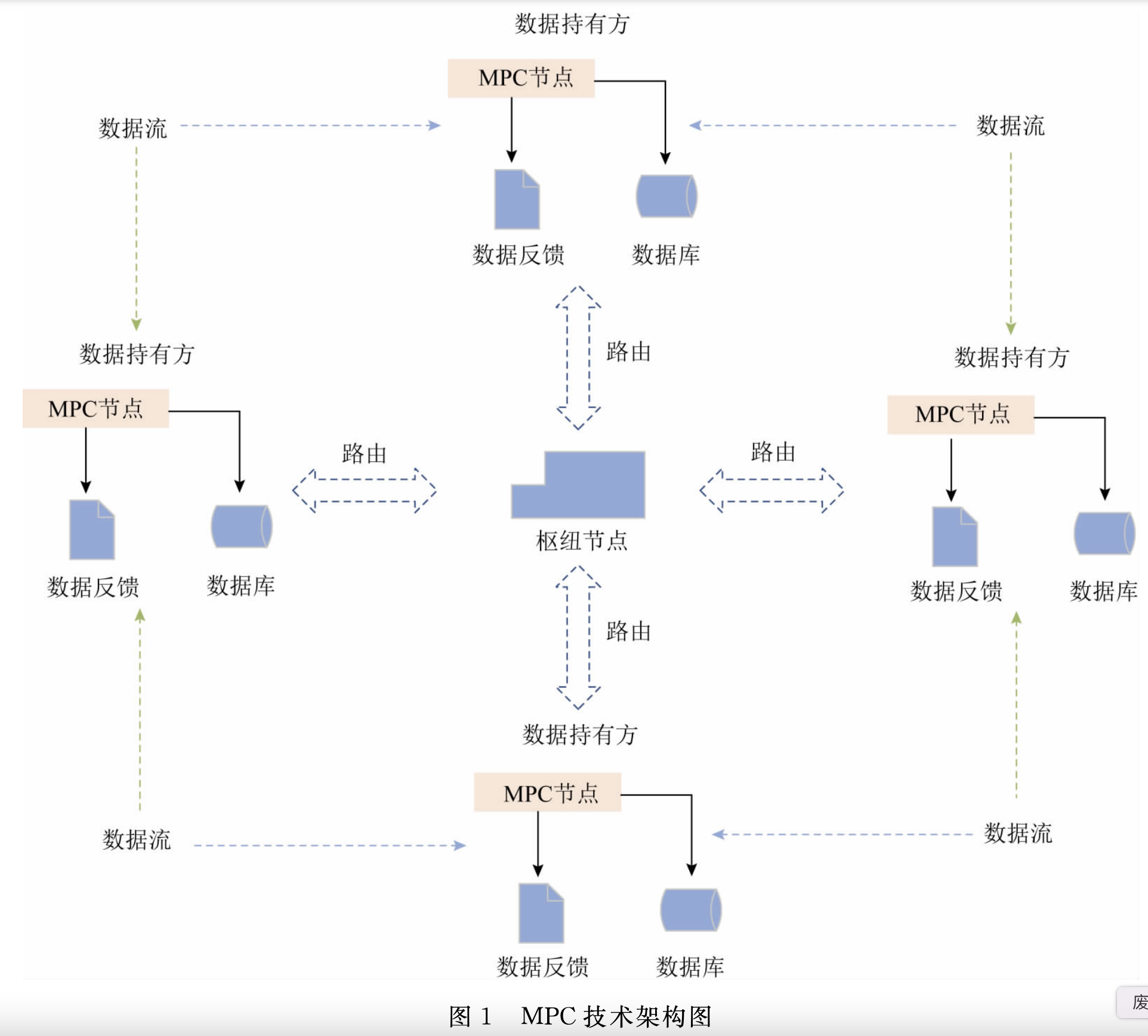
MPC 的特性

1. 输入隐私性：MPC 在进行计算任务时根据 MPC 节点的计算，从本地查询数据，再根据计算任务进行数据计算，整个过程中，数据都在本地数据库中保存，不存在数据泄露问题，因此保证了输入数据的隐私性。

2. 计算正确性：MPC 数据参与方根据约定进行任务计算，通过 MPC 协议进行计算数据的查询、协同计算，因此可以保证计算的正确性。

3. 去中心化：MPC 不存在有特权的参与方或可信第三方，而是采用协议的方式代替第三方，通过协议保证各数据参与方地位权力平等，任何数据拥有者都可开启计算任务。

MPC 模型组成部分

MPC 模型主要由４个部分组成：

1. 协议参与者
2. 协议攻击者
3. 网络条件
4. 通信信道

协议参与者

按照协议参与者在协议执行过程中的行为，可以把协议参与者分为：

1. 诚实的协议参与者：这类参与者是最理想的协议参与者，根据计算任务时约定好的过程，对照协议执行每个步骤。

2. 半诚实的协议参与者：这类参与者不会像诚实参与者一样按照协议进行每个步骤，它根据现实情况私下收集所需数据，推导其他参与者的输入数据和输入值，但不会主动攻击或联合其他数据参与者破坏协议。由于这类参与者由于不主动攻击和联合其他参与者，一般很难被检测到，这对协议的安全性影响很大，一旦半诚实参与者被买通或攻破，其收集到的数据就会被泄露。

3. 恶意参与者：这类参与者容易被攻击者买通，或者就是攻击者伪装形成的参与者，以此非法获取有用数据。

在现实情况下，主要存在的是半诚实协议参与者和恶意参与者，因此设计了半诚实模型和恶意敌手模型：

1. 半诚实模型（the semi-honst model）：在协议执行时参与者按照协议规定的流程执行，但是可能会被恶意攻击者监听获取到在协议执行过程中参与者的输入输出以及在协议运行过程中获得的信息。

2. 恶意敌手模型（the malicious mode）：在协议执行时，攻击者可以通过在其控制下的参与方进行不合法的输入，或者恶意篡改输入等方法来分析诚实参与者的隐私信息．还可以通过提前终止和拒绝参与等方式导致协议的终止。

协议攻击者

协议攻击者和协议恶意参与者参与协同计算的目的相同，都是通过非法途径来获取数据．与恶意参与者行为不同的是，它可以控制参与者，篡改协议参与者的步骤，使参与者按照其意愿继续执行协议来获取信息。

攻击者对不诚实参与者的控制可以分为以下 2 种情况：

1. 被动攻击/窃听者：仅仅窃听信道或者获取不诚实参与者在协同计算过程中所得到的信息，不诚实参与者仍然按照协议约定执行协议步骤。
2. 被动攻击者：攻击者会改变不诚实参与者的行为，不仅仅窃听或者获取不诚实参与者在协议进行中所得到的信息，还使其按照自己的意愿参与协议来达到窃取信息的目的。

网络条件

MPC 的各数据所有者在进行协同计算任务时都需要通过网络媒介进行连接。

• 在同步网络媒介中，所有的数据参与者将共同拥有同一个、全局性的时钟．所有的信息会在同一个时间段内送达，并且每个数据参与者都能在下一时间段内收到属于自己的数据信息。

• 在非同步网络媒介中，所有数据参与者无法拥有同一个、全局性的时钟。信息从某个数据参与者的本地数据库中发出去，需要经过若干个时间段，数据参与者的接收方才能收到属于自己的数据信息，并且收到的数据信息由于来自不同参与者，接收到的数据信息顺序可能不是真实的发送顺序。

通信信道

MPC 的参与者之间的网络媒介需要信道相连，来完成与其他参与者的数据交换。由于协议攻击者会对不诚实协议参与者进行一定程度的控制，所以将通信信道分为 3 个级别：

1. 安全信道：攻击者对于安全信道没有控制能力；
2. 非安全信道：攻击者对非安全信道可以窃听参与者的通信信息，但不能篡改内容；
3. 未认证信道：攻击者对未认证信道可以完全控制，甚至可以伪装成诚实的参与者参与协议。

MPC 的关键技术

实现 MPC 的关键密码学技术主要包括：

1. 同态加密（Homomorphic Encryption，HE）
2. 秘密共享（Secret Sharing，SS）
3. 混淆电路（Garbled Circuit，GC）
4. 不经意传输（Oblivious Transfer，OT）
5. 等。

目前来说，MPC 主要是通过混淆电路和秘密共享这两种方式来实现。

• 基于混淆电路的协议更适用于两方逻辑运算，通讯负担较低，但拓展性较差。
• 基于秘密分享的安全多方计算其拓展性较强，支持无限多方参与计算，计算效率高，但通讯负载较大。

秘密共享

秘密共享常被用于多方安全签名，用于保护重要信息不被丢失、不被篡改。

通过秘密共享机制，秘密信息会被拆分，每个参与者仅持有该秘密的一部分，个人持有部分碎片无法用于恢复秘密，需要凑齐预定数量 (或门限) 的碎片才可以。

例子：假设，A、B 和 C 想知道三人的平均薪资，但又不想透露自己的具体薪资，那么要用什么方法达到这个目的呢？

解决方法 1：传统的，如果有可信第三方的话，问题很容易解决。比如，A、B 和 C 有一个共同信任的老板，大家可以各自把自己的工资告诉老板，老板保证不泄漏任何一位的薪资，并计算出三人的平均薪资。最后，将平均薪资告诉大家。

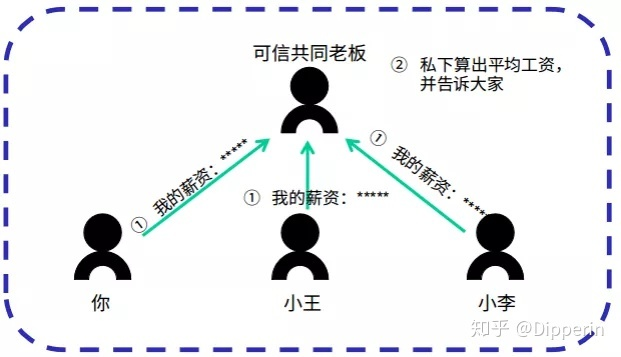
解决方法 2：现实中并不是总能找到这样的可信第三方。在这种情况下，就能使用安全多方计算来解决问题了。简而言之，就是用算法代替可信第三方。

一种容易理解的基于秘密共享的 MPC 协议。首先我们需要回顾一下一个简单的数学理论，2 点可以确定一条直线，3 点确定一条抛物线。

1. A、B 和 C，各自选择一条抛物线，抛物线和 Y 轴的交点是自己的工资数。比如 A 的工资是 100，选择了一条抛物线 y = 2x2 + x + 100，然后，在这条抛物线上取出 3 个点（1, 103），（2, 110），（3, 121）。自己保留一个点（1 , 103），并秘密地将另外两个点（2, 110），（3, 121）的信息分别加密传给 B 和 C。同样的，B 和 C 也做这样的操作，将 x=1 的点秘密地传给 A，x=2 的点给 B，x=3 的点给 C。

2. 此时，每人都拥有了 3 个密码碎片（不同抛物线上的点），A 拥有（1, 103），来自 B 的（1, y2），C 的（1, y3）。A 就可以算出一个点（1, 103+y2+y3）。这个点在一条特殊的抛物线上，这条抛物线与 y 轴的截距正好是 3 人的薪资之和。

3. 三人将各自算出的不同的 3 个点，一起还原出一条抛物线。得到抛物线的截距。将截距除以 3，得到的值就是三个人的薪资之和了。

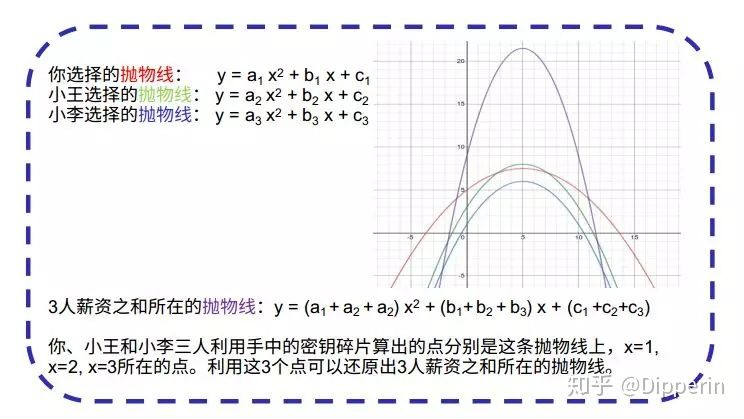
这种秘密共享的方案下，一方面，三个人的薪资是保密的。因为，每个人只得到了对方抛物线的一个点，无法还原出对方的抛物线，因此无法算出截距，也就是别人的工资。并且，如果 B 和 C 合谋，他们也是无法算出 A 的薪资的，因为他们手中关于 A 薪资的抛物线，只掌握了 2 个点。但 2 个点仍然无法还原出抛物线，因为，3 点确定一条抛物线。另一方面， 还可以计算出三个人的薪资之和。A，B 和 C，三条抛物线之和得到的抛物线，的截距必定等于三个抛物线的截距之和。

混淆电路（Garbled Circuit）

混淆电路是一种密码学协议，遵照这个协议，两个参与方能在互相不知晓对方数据的情况下计算某一函数。

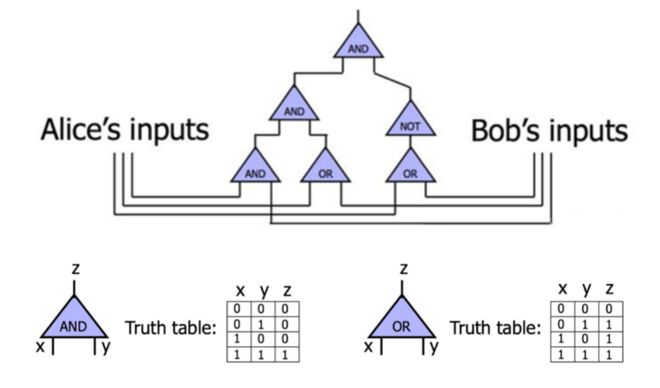
不经意传输（Oblivious Transfer）

不经意传输是一种密码学协议，它解决了问题：Alice 手上有两组密封的密码组合，Bob 只能获得一组密码且 Bob 希望 Alice 不知道他选择哪一组密码。这时候就能利用不经意传输来完成交易。

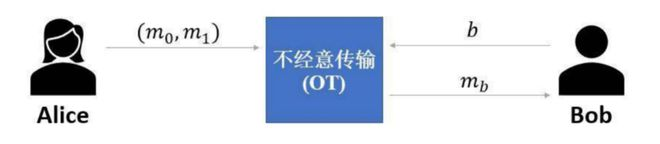
零知识证明

零知识证明存在双方或多方角色：

• 示证者（Prover）：宣称某一命题为真。
• 验证者（Verifier）：确认该命题是否为真。

零知识证明指的是示证者能够在不向验证者提供任何有用的信息的情况下，使验证者相信某个论断是正确的。

MPC 的开源项目

1. 谷歌开源了多方安全计算工具 Private Join and Compute，以帮助组织和机构协同处理机密数据集；
2. 脸书将安全机器学习（Secure Machine Learning）框架 CrypTen 开源。
3. 华控清交基于多方安全计算技术，实现了高性能通用的安全计算框架 PrivPy 平台。
4. 矩阵元推出了隐私机器学习开源框架 Rosetta。

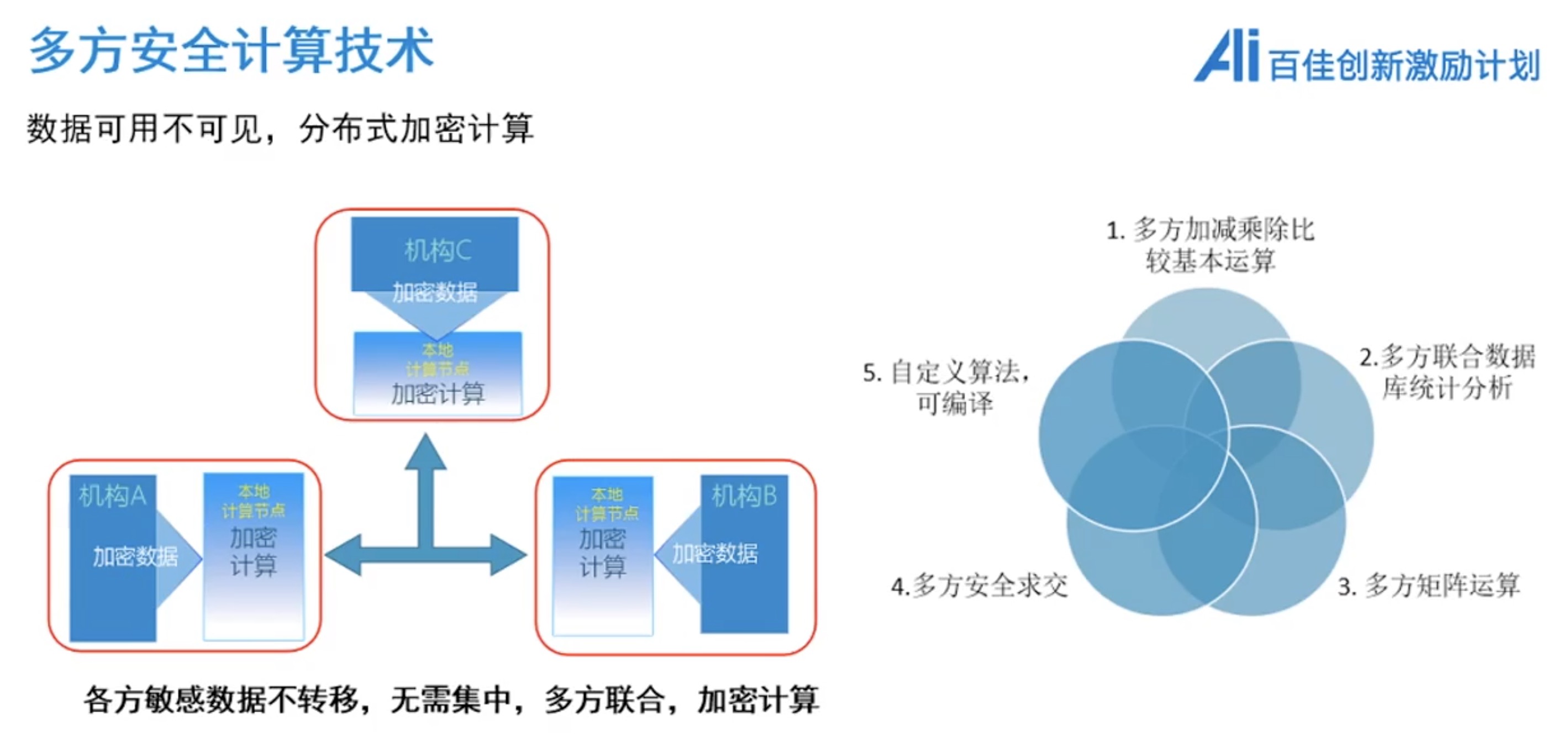
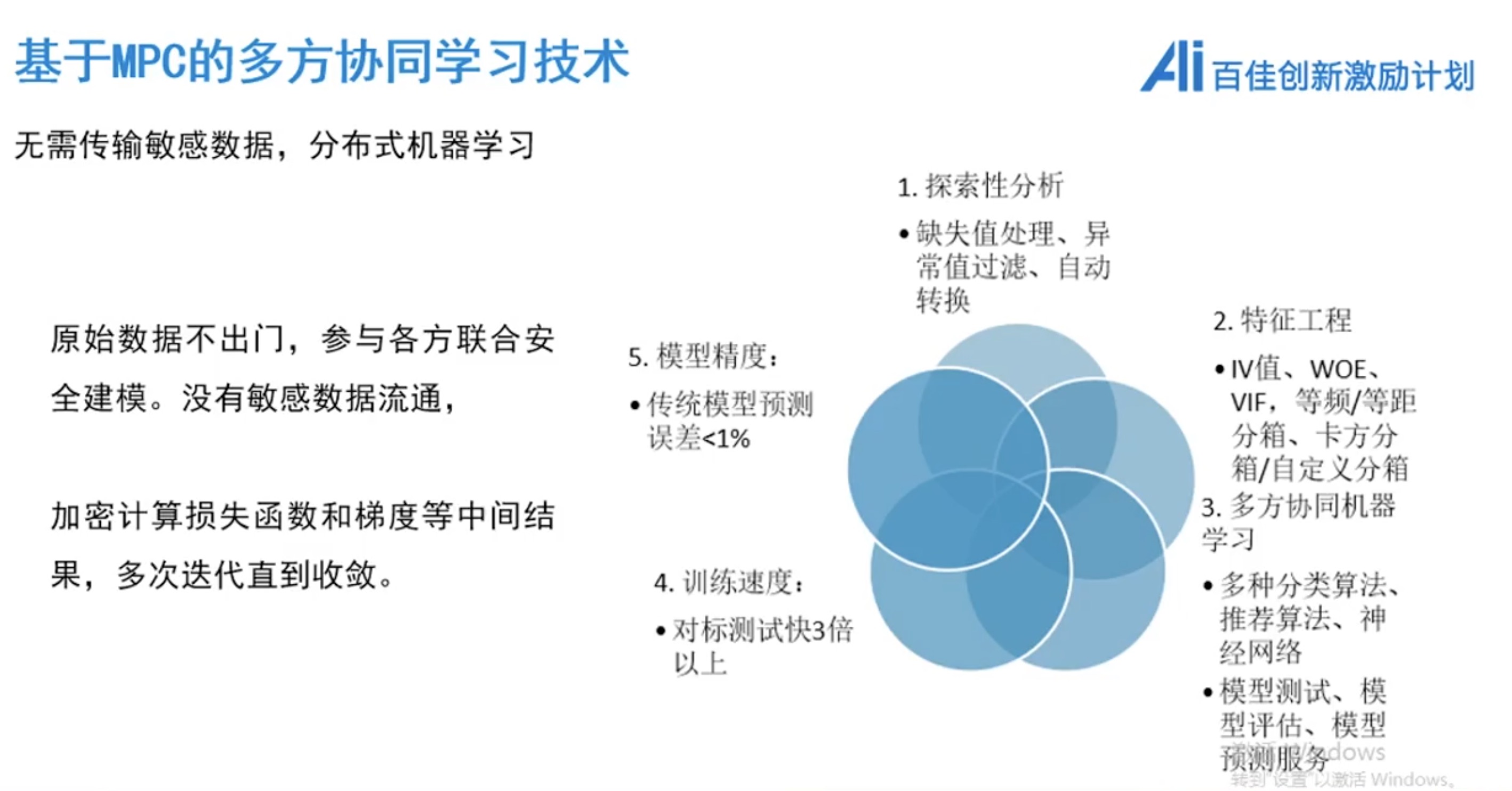
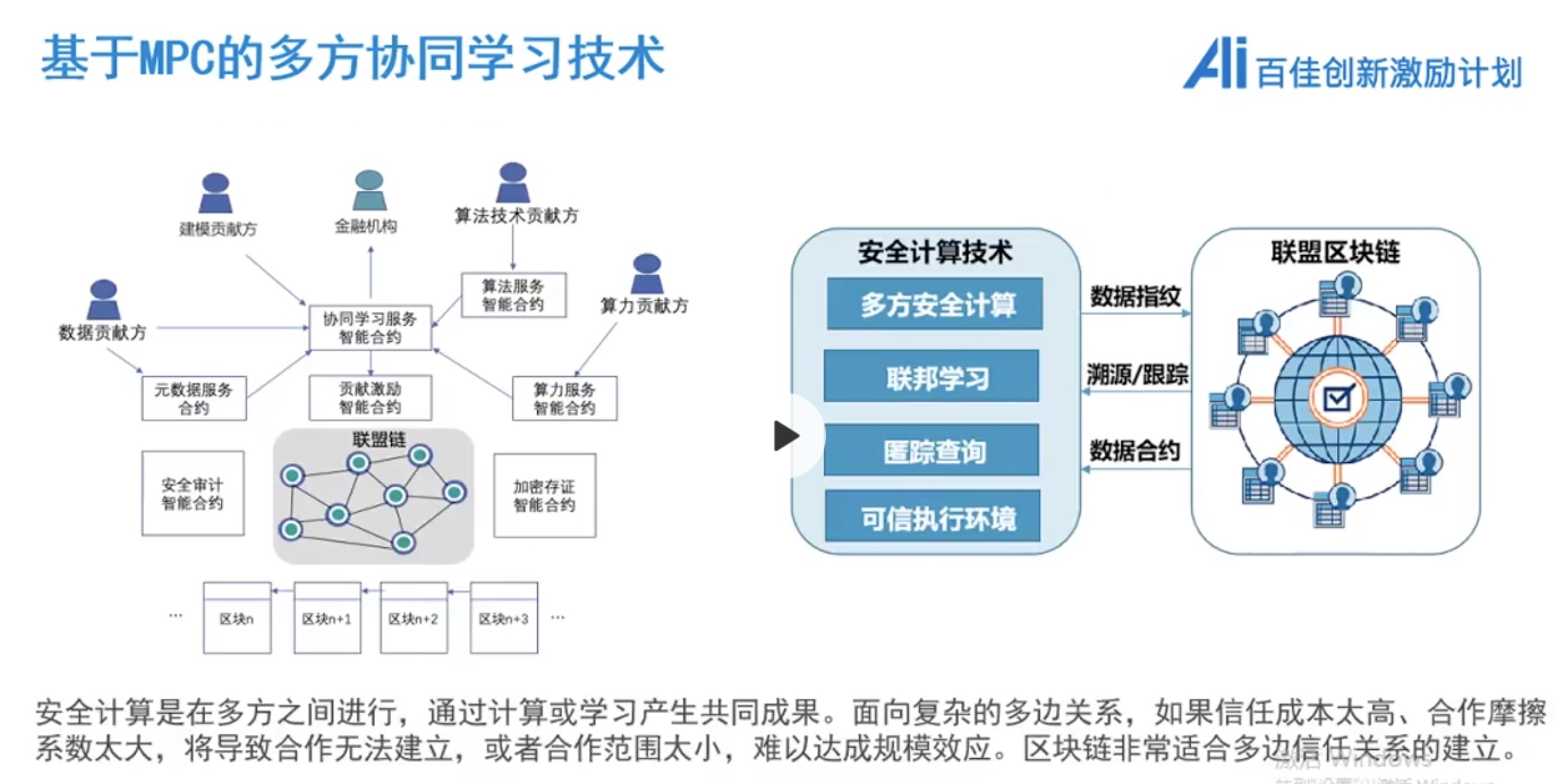
MPC + 联邦学习

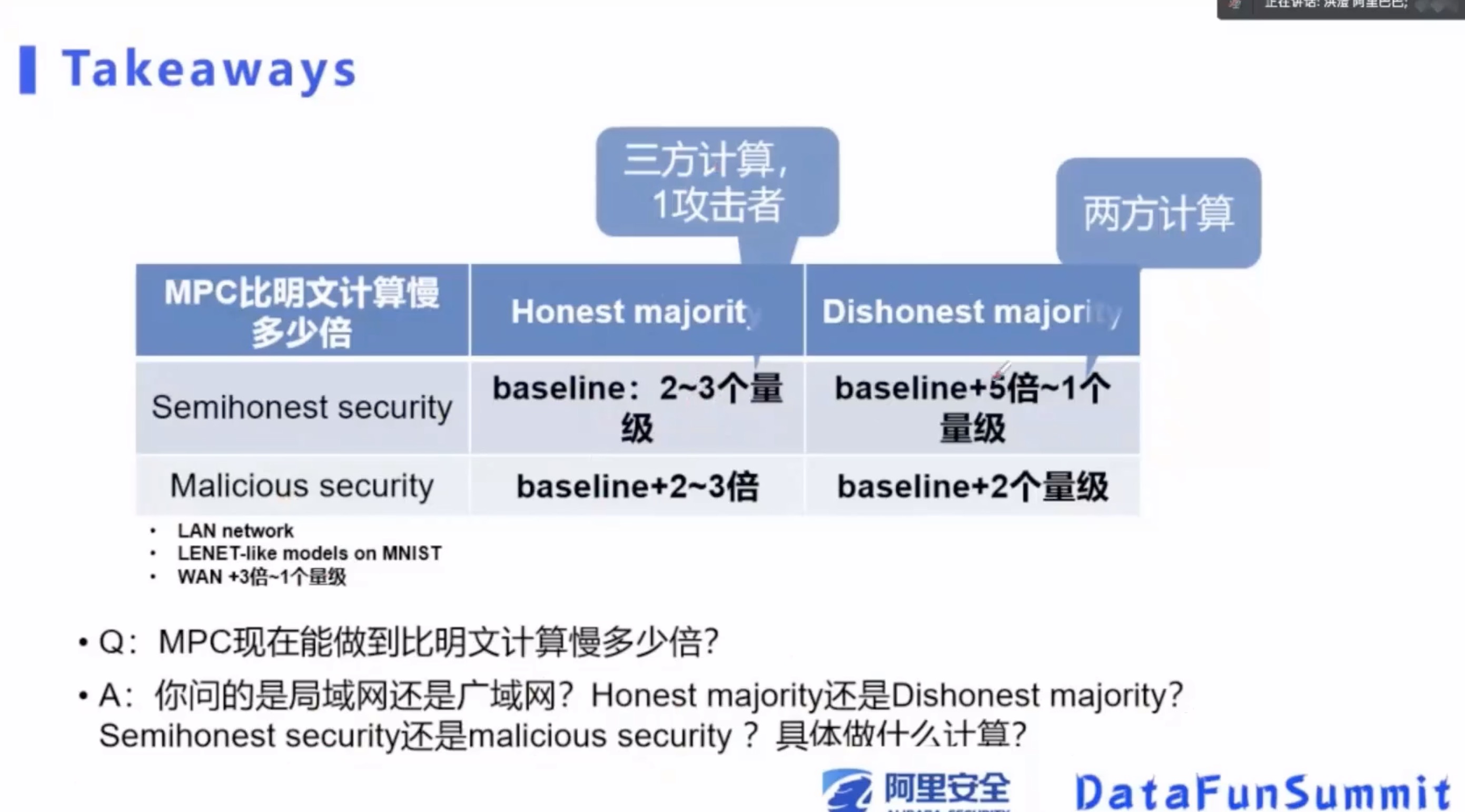
MPC 的性能问题

文章来源: is-cloud.blog.csdn.net，作者：范桂飓，版权归原作者所有，如需转载，请联系作者。

原文链接：is-cloud.blog.csdn.net/article/details/125746037