数据挖掘从入门到放弃（四）：手撕（绘）关联规则挖掘算法

友情提示:篇幅较长、多图（手绘）,请备好流量。

关联规则简介

关联规则挖掘可以让我们从数据集中发现项与项之间的关系，它在我们的生活中有很多应用场景，“购物篮分析”就是一个常见的场景，这个场景可以从消费者交易记录中发掘商品与商品之间的关联关系，进而通过商品捆绑销售或者相关推荐的方式带来更多的销售量。

1. 搞懂关联规则中的几个重要概念：支持度、置信度、提升度

2. Apriori 算法的工作原理

3. 在实际工作中，我们该如何进行关联规则挖掘

关联规则中重要的概念

我举一个超市购物的例子，下面是几名客户购买的商品列表：

订单编号	购买商品
1	牛奶、面包、尿布
2	可乐、面包、尿布、啤酒
3	牛奶、尿布、啤酒、鸡蛋
4	面包、牛奶、尿布、啤酒
5	面包、牛奶、尿布、可乐

支持度

支持度是个百分比，它指的是某个商品组合出现的次数与总次数之间的比例。支持度越高，代表这个组合出现的频率越大。

我们看啤酒出现了3次，那么5笔订单中啤酒的支持度是3/5=0.6。同理，尿布出现了5次，那么尿布的支持度是5/5=1。尿布和啤酒同时出现的支持度是3/6=0.6。

置信度

它指的就是当你购买了商品 A，会有多大的概率购买商品 B。

我们可以看上面的商品，购买尿布的同时又购买啤酒的订单数是3，购买啤酒的订单数是3，那么（尿布->啤酒）置信度= 3/3=1。

再看购买了啤酒同时购买尿布的订单数是3，购买尿布的订单数是5，那么（啤酒->尿布）置信度=3/5=0.6。

提升度

提升度代表的是“商品 A 的出现，对商品 B 的出现概率提升的”程度。所以我们在做商品推荐的时候，重点考虑的是提升度。

我们来看提升度公式： 那么我们来计算下尿布对啤酒的提升度是多少： 

怎么解读1.67这个数值呢？

1. 提升度 (A→B)>1：代表有提升

2. 提升度 (A→B)=1：代表有没有提升，也没有下降

3. 提升度 (A→B)<1：代表有下降。

其实看上面提升度的公式，我们就可以理解，也就是AB同时出现的次数越多，单独出现B的次数越少，那么支持度也就越大也就是B的出现总是伴随着A的出现，那么A对B出现的概率就越有提升！

Apriori 的工作原理

我们一起来看下经典的关联规则 Apriori 算法是如何工作的。

Apriori 算法其实就是查找频繁项集 (frequent itemset) 的过程，所以我们需要先了解是频繁项集。

频繁项集就是支持度大于等于最小支持度阈值的项集，所以小于最小值支持度的项目就是非频繁项集，而大于等于最小支持度的项集就是频繁项集。

下面我们来举个栗子：

假设我随机指定最小支持度是0.2。首先，我们先计算单个商品的支持度：

购买商品	支持度
牛奶	4/5
面包	4/5
尿布	5/5
可乐	2/5
啤酒	3/5
鸡蛋	1/5

因为最小支持度是 0.2，所以你能看到商品 鸡蛋 是不符合最小支持度的，不属于频繁项集，于是经过筛选商品的频繁项集如下：

购买商品	支持度
牛奶	4/5
面包	4/5
尿布	5/5
可乐	2/5
啤酒	3/5

在这个基础上，我们将商品两两组合，得到两个商品的支持度：

购买商品	支持度
牛奶、面包	3/5
牛奶、尿布	4/5
牛奶、可乐	1/5
牛奶、啤酒	2/5
面包、尿布	4/5
面包、可乐	2/5
面包、啤酒	2/5
尿布、可乐	2/5
尿布、啤酒	3/5
可乐、啤酒	1/5

筛选大于最小支持度（0.2）的数据后

购买商品	支持度
牛奶、面包	3/5
牛奶、尿布	4/5
牛奶、啤酒	2/5
面包、尿布	4/5
面包、可乐	2/5
面包、啤酒	2/5
尿布、可乐	2/5
尿布、啤酒	3/5

在这个基础上，我们再将商品三个组合，得到三个商品的支持度：

购买商品	支持度
牛奶、面包、尿布	3/5
牛奶、面包、可乐	1/5
牛奶、面包、啤酒	1/5
面包、尿布、可乐	1/5
面包、尿布、啤酒	2/5
尿布、可乐、啤酒	1/5

筛选大于最小支持度（0.2）的数据后

购买商品	支持度
牛奶、面包、尿布	3/5
面包、尿布、啤酒	2/5

在这个基础上，我们将商品四个组合，得到四个商品的支持度：

购买商品	支持度
牛奶、面包、尿布、可乐	1/5
牛奶、面包、尿布、啤酒	1/5
面包、尿布、可乐、啤酒	1/5

再次筛选大于最小支持度（0.2）数据的话，就全删除了，那么，此时算法结束，上一次的结果就是我们要找的频繁项，也就是{牛奶、面包、尿布}、{面包、尿布、啤酒}。

我们来总结一下上述Apriori算法过程：

1. K=1，计算 K 项集的支持度

2. 筛选掉小于最小支持度的项集

3. 如果项集为空，则对应 K-1 项集的结果为最终结果

4. 否则 K=K+1，重复 1-3 步

我们可以看到 Apriori 在计算的过程中有以下几个缺点：

1. 可能产生大量的候选集。因为采用排列组合的方式，把可能的项集都组合出来了

2. 每次计算都需要重新扫描数据集，来计算每个项集的支持度

这就好比我们数据库中的“全表扫描”查询一样，非常浪费IO和时间。在数据库中我们都知道使用索引来快速检索数据，那Apriori 能优化吗？

Apriori 的改进算法：FP-Growth 算法

FP-growth算法是基于Apriori原理的，通过将数据集存储在FP树上发现频繁项集，但不能发现数据之间的关联规则。FP-growth算法只需要对数据库进行两次扫描，而Apriori算法在求每个潜在的频繁项集时都需要扫描一次数据集，所以说Apriori算法是高效的。其中算法发现频繁项集的过程是：(1)构建FP树；(2)从FP树中挖掘频繁项集。

创建项头表

概念知识不在这凑字数了，我们直接来干货！假设我们从以下数据中来挖掘频繁项。

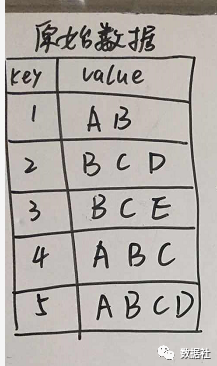
首先创建，项头表，这一步的流程是先扫描一遍数据集，对于满足最小支持度的单个项按照支持度从高到低进行排序，这个过程中删除了不满足最小支持度的项（假设最小支持度是0.2）。

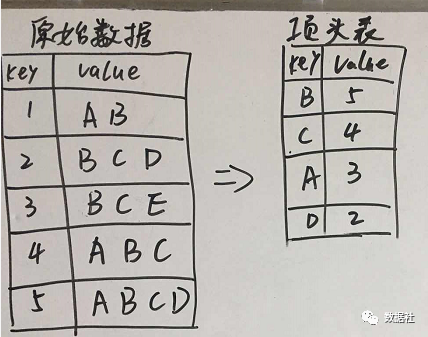
构建FP树

整个流程是需要再次扫描数据集，对于每一条数据，按照支持度从高到低的顺序进行创建节点（也就是第一步中项头表中的排序结果），节点如果存在就将计数 count+1，如果不存在就进行创建。同时在创建的过程中，需要更新项头表的链表。

先把原始数据按照支持度排序，那么原始数据变化如下：

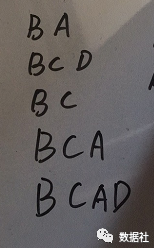
下面我们把以上每行数据，按照顺序插入到FP树中，注意FP树的根节点记为 NULL 节点。

接下来插入第二行数据，由于第二行数据第一个数据也是B，和已有的树结构重合，那么我们保持原来树结构中的B位置不变，同时计数加1，C、D是新增数据，那么就会有新的树分叉，结果如下图：

以此类推，读取下面的三行数据到FP树中

最后生成的FP数如下：

根据FP数挖掘频繁项

我们终于把FP树建立好了，那么如何去看这颗树呢？得到 FP 树后，需要对每一个频繁项，逐个挖掘频繁项集。具体过程为：首先获得频繁项的前缀路径，然后将前缀路径作为新的数据集，以此构建前缀路径的条件 FP 树。然后对条件 FP 树中的每个频繁项，获得前缀路径并以此构建新的条件 FP 树。不断迭代，直到条件 FP 树中只包含一个频繁项为止（反正我第一次看完这句话是没理解）。

FP树是从下往上看了，也就是根据子节点找父节点，接下来还是来图解~

首先，我们看包含A的频繁项：

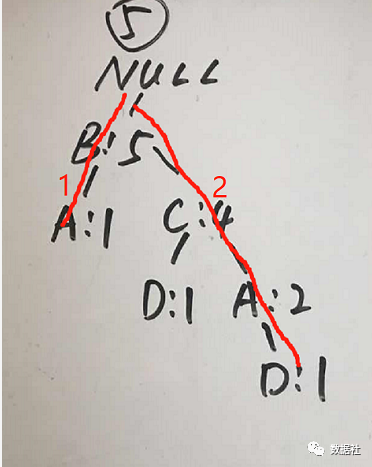
我们可以看到包含A的树有两个，我们先看树2，可以得到路径{B:2,C:2}，此处的2是根据A出现的次数定的。接着我们创建FP树，具体的创建过程和上面创建 FP 树的过程一样，如下图：

注意此时头指针表中包含两个元素，所以对每个元素，需要获得前缀路径，并将前缀路径创建成条件 FP 树，直到条件 FP 树中只包含一个元素时返回。

• 对元素 B，获得前缀路径为{}，则频繁项集返回{A:2,B:2};

• 对元素 C，获得前缀路径{B:2}，则将前缀路径创建成条件 FP 树，如下图  所示。

  注意此时条件 FP 树中只包含一个元素，故返回频繁项集{A:2,C:2,B:2}。由于元素 C 也是频繁项，所以{A:2,C:2}也是频繁项集。

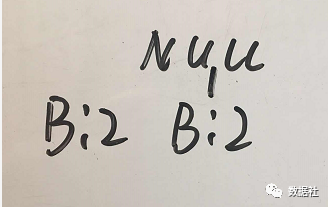
再加上{A:2}本身就是频繁项集，所以 A 对应的频繁项集有：{A:2},{A:2,C:2} ,{A:2,B:2},{A:2,C:2,B:2}。

同理，我们来看树1，树1比较简单，就一个路径{B:1}，根据上述方法我们得到此分支频繁项为{A:1,B:1},{A:1}。

综上，我们可以看到两个分支都包含频繁项{A,B},{A}的，此时我们进行合并两个分支，得到包含A的频繁项：{A:3},{A:3,B:3},{A:2,C:2} ,{A:2,C:2,B:2}，我们用出现的次数转换下，即 (A,): 3, (A, B): 3, (A, C): 2, (A, B, C): 2。

同理，按照上述方法，我们可以依次找到包含B的频繁项是(D): 2, (C, D): 2, (B, D): 2, (B, C, D): 2,  (C): 4, (B, C): 4, (B): 5。

实践总结

经典的算法，很多大神已经实现，我们直接拿来用就行了，比如上面的FP-GROWTH算法，介绍一款专门的包pyfpgrowth。

代码：

import pyfpgrowth as fp

itemsets = [['A','B'], ['B','C','D'],['B','C'],['A','B','C'],['A','B','C','D']]

# 频数删选  频数大于2
patterns = fp.find_frequent_patterns(itemsets, 2)

print(patterns)

{('D',): 2, ('C', 'D'): 2, ('B', 'D'): 2, ('B', 'C', 'D'): 2, ('A',): 3, ('A', 'B'): 3, ('A', 'C'): 2, ('A', 'B', 'C'): 2, ('C',): 4, ('B', 'C'): 4, ('B',): 5}

很对人会问算法原理看着很费劲，直接两行代码搞定。我们还看原理干嘛，直接写（抄）代码不就行了。我举个例子哈，记得上小学3年级的时候，有一次数学考试，老师出了一道附加题：

附加题（10分）：求1+2+3+…+99+100的和。提示：参考梯形面积计算公式。

当然，对于一个初中生，这道题很好解答，但对于一个小学三年级的学生来说还是比较难的。但是，我知道梯形的计算公式：

梯形面积 = （上底+下底）×高÷2

所以，就按照这个计算了

1+2+3+…+99+100 = (1 + 100)x100÷2

其实，算法原理也是一样，我们了解后，可以举一反三的使用，并不一定总是在一个场景下使用的。

---

历史好文推荐

1. 数据挖掘从入门到放弃（一）：线性回归和逻辑回归
   

2. 数据挖掘从入门到放弃（二）：决策树
   

3. 数据挖掘从入门到放弃（三）：朴素贝叶斯
   

4. kafka实战宝典：手动修改消费偏移量的两种方式

5. Kafka实战宝典：如何跨机房传输数据