前言

Hello！
非常感谢您阅读海轰的文章，倘若文中有错误的地方，欢迎您指出～
 
自我介绍 ଘ(੭ˊᵕˋ)੭
昵称：海轰
标签：程序猿｜C++选手｜学生
简介：因C语言结识编程，随后转入计算机专业，获得过国家奖学金，有幸在竞赛中拿过一些国奖、省奖…已保研。
学习经验：扎实基础 + 多做笔记 + 多敲代码 + 多思考 + 学好英语！
 
唯有努力💪
 

知其然 知其所以然！

 
本文仅记录自己感兴趣的内容

题目1

取整函数 $\lfloor x\rfloor ，\lceil x\rceil$满足$x-1<\lfloor x\rfloor \le x\le \lceil x\rceil <x+1$，设$a,b,n$为正整数，证明如下

（1）$\lceil \frac{n}{a}\rceil \le \frac{n}{a}+\frac{a-1}{a}$

（2）$\lceil \frac{\lceil \frac{n}{a}\rceil }{b}\rceil =\lceil \frac{n}{ab}\rceil$

（3）$\lfloor \frac{n}{2}\rfloor +\lceil \frac{n}{2}\rceil =n$

证明：

$\frac{n}{2}-1<\lfloor \frac{n}{2}\rfloor \le \frac{n}{2}$

同时加上$\frac{n}{2}$

$\frac{n}{2}-1+\frac{n}{2}<\lfloor \frac{n}{2}\rfloor +\frac{n}{2}\le \frac{n}{2}+\frac{n}{2}$

即

$n-1<\lfloor \frac{n}{2}\rfloor +\frac{n}{2}\le n$

因为$n$是正整数

$\lfloor \frac{n}{2}\rfloor$也一定是一个正整数

若$\frac{n}{2}$不是整数，则一定有

$n-1<\lfloor \frac{n}{2}\rfloor +\frac{n}{2}<n$

若$\frac{n}{2}$是整数，则一定有

$n-1<\lfloor \frac{n}{2}\rfloor +\frac{n}{2}<=n\Rightarrow \lfloor \frac{n}{2}\rfloor +\frac{n}{2}=n$

所以

$\lfloor \frac{n}{2}\rfloor +\frac{n}{2}$的上限就是$n$

综上，下面等式成立

$n-1<\lfloor \frac{n}{2}\rfloor +\lceil \frac{n}{2}\rceil <=n$

即

$\lfloor \frac{n}{2}\rfloor +\lceil \frac{n}{2}\rceil =n$

（4）$\lfloor n+1\rfloor =\lfloor n\rfloor +1$

题目2

参考资料

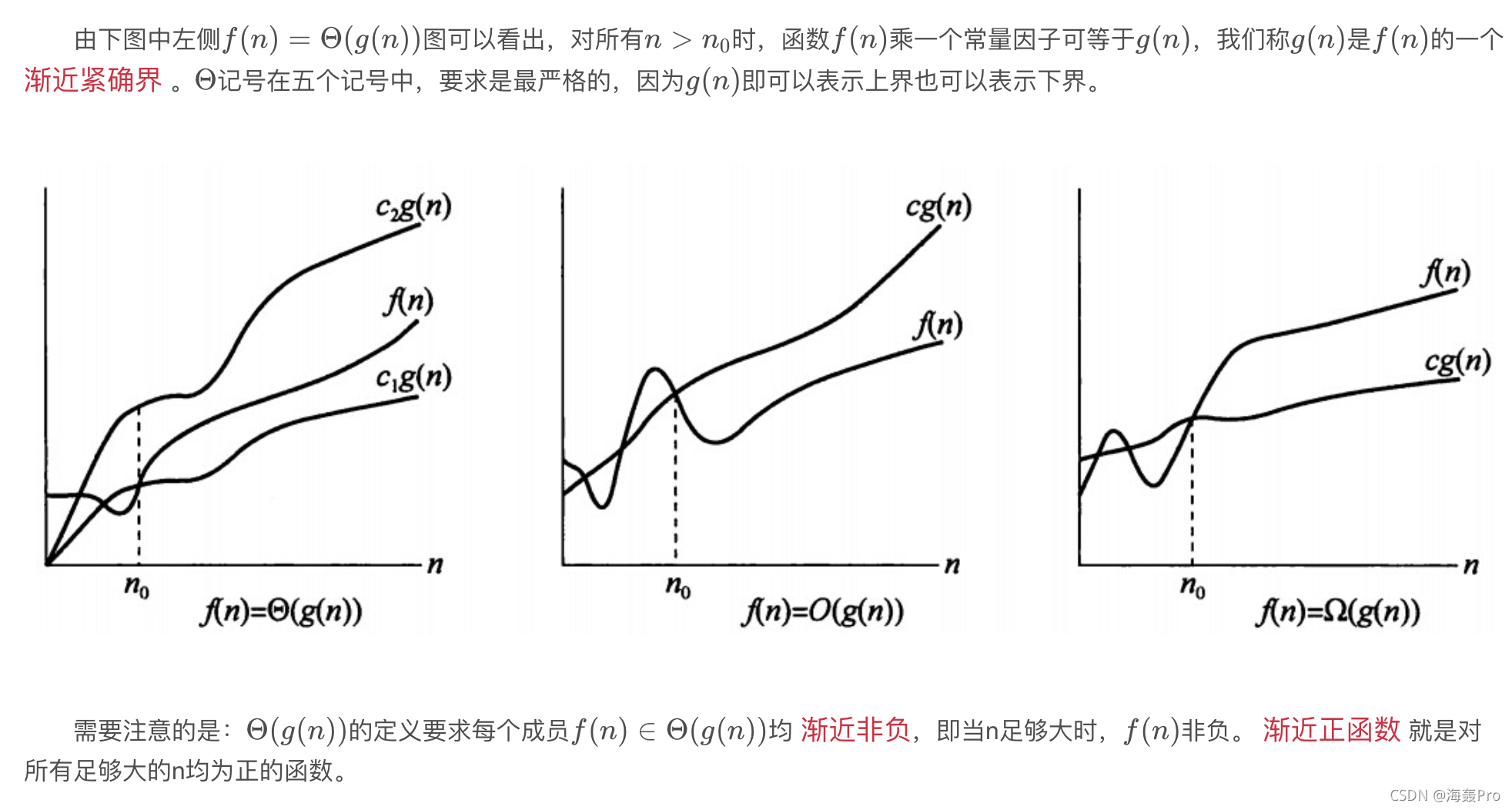
注：有些不全 来自师兄师姐的复习资料 字太多了 打不完

结语

文章仅作为个人学习笔记记录，记录从0到1的一个过程

希望对您有一点点帮助，如有错误欢迎小伙伴指正

文章来源: haihong.blog.csdn.net，作者：海轰Pro，版权归原作者所有，如需转载，请联系作者。

原文链接：haihong.blog.csdn.net/article/details/126847136