【数据结构】栈与队列
文章目录
3.栈与队列
3.1 概述
-
比较重要,且应用广泛的两种线性结构:栈 Stack、队列 Queue。
-
栈和队列 与 线性表不同之处:栈和队列可被看成是两种
操作受限的特殊线性表。
3.2 栈
3.2.1 定义
-
栈是一个特殊的线性表,插入和删除只允许在
栈顶Top(线性表的尾端)进行操作。 -
术语:
-
栈顶Top:允许进行插入和删除的一端。
-
栈底Bottom
-
入栈push:栈的插入操作。
-
出栈pop:栈的删除操作。
-

-
栈特点:后进先出(Last In First Out、LIFO)、先进后出(First In Last Out、FILO)。
3.2.2 出入栈练习(卡特兰数)
-
需求:若将ABCD依次入栈,则出栈的序列是?(进出栈可以交替进行)
// 入栈个数 1/2/3/4 Ain Aout Bin Bout Cin Cout Din Dout --> ABCD Ain Aout Bin Bout Cin Din Dout Cout --> ABDC Ain Aout Bin Cin Cout Din Dout Bout --> ACDB Ain Aout Bin Cin Cout Bout Din Dout --> ACBD Ain Aout Bin Cin Din Dout Cout Bout --> ADCB Ain Bin Bout Aout Cin Cout Din Dout --> BACD Ain Bin Bout Aout Cin Din Dout Cout --> BADC Ain Bin Bout Cin Cout Aout Din Dout --> BCAD Ain Bin Bout Cin Cout Din Dout Aout --> BCDA Ain Bin Bout Cin Din Dout Cout Aout --> BDCA Ain Bin Cin Cout Din Dout Bout Aout --> CDBA Ain Bin Cin Cout Bout Din Dout Aout --> CBDA Ain Bin Cin Cout Bout Aout Din Dout --> CBAD Ain Bin Cin Din Dout Cout Bout Aout --> DCBA
-
进出栈是最经典的
卡特兰数Cn2nn+1https://zhuanlan.zhihu.com/p/97619085
3.3 顺序栈
3.3.1 定义
-
顺序栈:使用数组实现的栈。
-
约定:
-
空栈:
top == 0 -
满栈:
top == stackElem.length -
长度:
top -
栈顶元素:
stackElem[top - 1]
-
3.3.2 栈类
public class SqStack {
private Object[] stackElem; //栈对象数组
private int top; //长度、下一个存储位置 等
}
3.3.3 算法:入栈【重点】
-
算法1:
public void push(Object x) {
if(top == stackElem.length) { //栈满
throw new RuntimeException("栈满");
} else {
stackElem[top] = x;
top++;
}
}
-
算法2:
public void push(Object x) {
if(top == stackElem.length) { //栈满
throw new RuntimeException("栈满");
} else {
stackElem[top++] = x;
}
}
3.3.4 算法:出栈【重点】
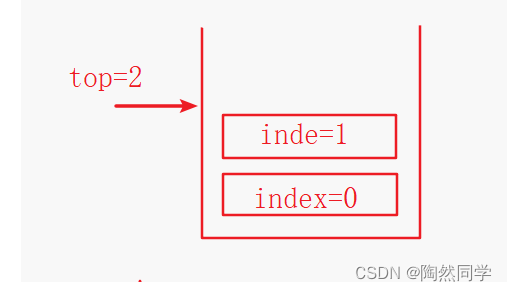
-
算法1:
public Object pop() { if(top == 0) { return null; //空栈 } else { top--; return stackElem[top]; } } -
算法2:
public boolean isEmpty() { //是否为空 return top == 0; } public Object pop() { if(isEmpty()) { return null; //空栈 } else { return stackElem[--top]; } }
3.4 链栈
3.4.1 定义
-
使用链式存储的栈,就是链栈。进行插入和删除操作在栈顶进行,也就是链表的尾端。
-
存储单元2部分组成:数据域 data 和指针域 next。
-
使用top栈顶指针用于指向栈尾。

3.4.2 栈类
public class LinkStack {
private Node top; //栈顶指针
}
3.4.3 算法:入栈
-
需求:将新结点p,压入到栈顶
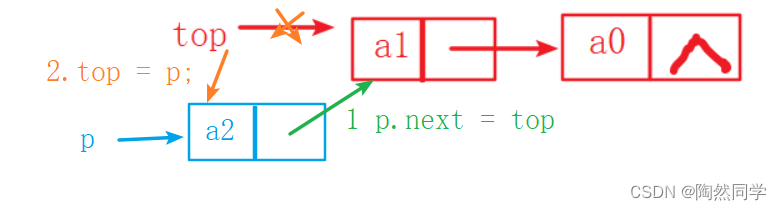
public void push(Object x) {
Node p = new Node(x); // 创建新结点p
p.next = top; // 1.p的指针域指向栈顶元素
top = p; // 2.栈顶指针top指向新结点p
}
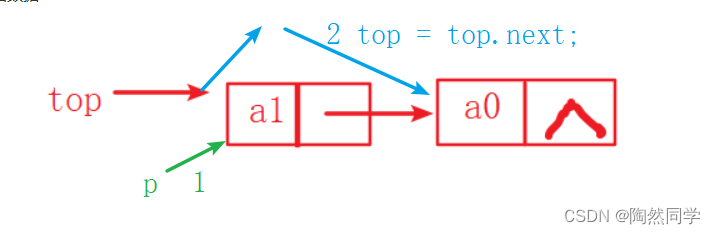
3.4.4 算法:出栈
-
需求:弹出栈顶元素,需要返回数据

public Object pop() {
if(top == null) { //空栈 isEmpty()
return null;
} else {
Node p = top; // 1 存放栈顶元素
top = top.next; // 2 将top指向栈顶的下一个元素
return p.data; // 3 返回栈顶元素数据
}
}
3.5 栈的应用
3.5.1 大数加法
p76
9992992347234947324732498327427342472987427427984724274 + 9990920943824283492834824820984028348204209384029293
-
思路:9293 + 978
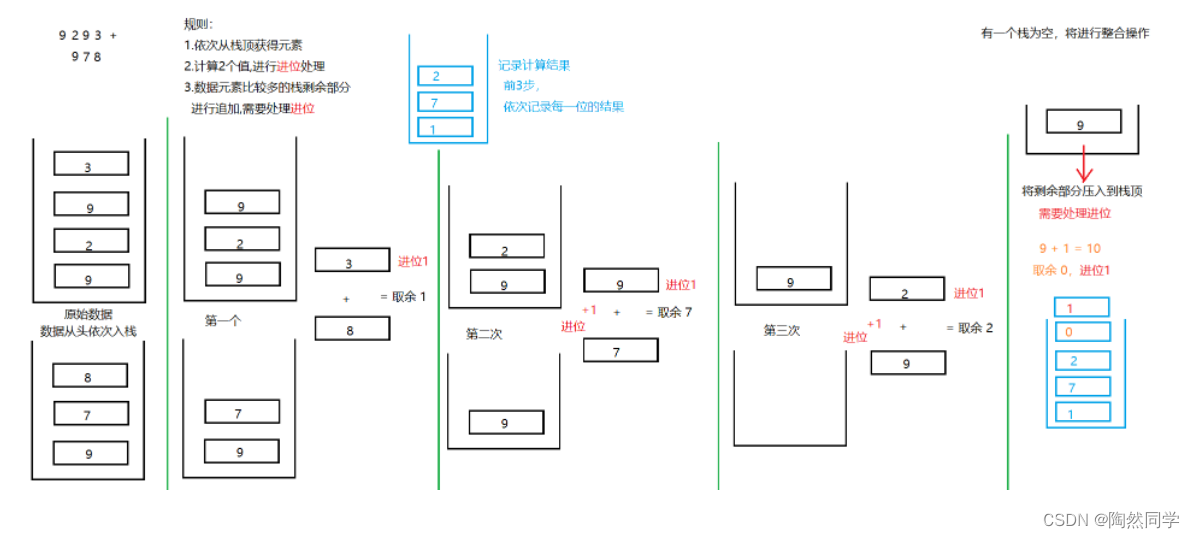
3.5.2 后缀表达式
p79
-
中序表达式:日常生活中编写的都是中序表达式。
a + b - c
-
后缀表达式:把运算符写在后面的表达式,也称为
逆波兰记法中序:a+b 后缀:ab+ 中序:a + b - c 后缀:ab+c- 中序:a + b * c 后缀:abc*+
-
除运算符之外的内容,依次填写
-
使用一个栈记录运算符
-
入栈:新入栈的运算符比栈里的运算符优先级要高。如果是
(进行入栈操作 -
出栈:新入栈的运算符没有栈里的运算符优先级高,栈里的运算符需要出栈,新运算符入栈。如果是
)出栈直到(
-
-
-
将以下
中序表达式转换成后续表达式
中序:8-(3+2*6)/5+2^2 后缀:8326*+5/-22^+ 中序:2*9+3-2*(10-3)/14 后缀:29*3+2103-*14/- 中序:A+B*(C*D-E) 后缀:ABCD*E-*+ 中序:a+b*c+(d*e+f)*g 后缀:abc*+de*f+g*+ 中序:9+(3-1)*3+10/2 后缀:931-3*+102/+
3.5.3 汉诺塔 Hanoi
-
游戏规则 (P84)
共3个柱子,在一根柱子上,从下往上按照大小顺序摞着N片圆盘。把圆盘开始按大小顺序重新摆放在另一根柱子上 规定:在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。
-
算法
package hanoi;
/**
* @author 桐叔
* @email liangtong@itcast.cn
*/
public class TestHanoi {
private static int count = 0;
/**
*
* @param n 需要移动的盘子数
* @param x 第一个柱子 起始
* @param y 第二个柱子 过渡
* @param z 第三个柱子 最后
*/
public static void hanoi(int n, char x, char y , char z) {
if(n == 1) { //只有一个盘子
move(x, 1, z);
} else {
hanoi(n-1, x, z ,y); // n上面的盘子,从x柱子,通过z柱子,移动到y柱子
move(x, n, z); //n盘子,从x柱子,移动到z柱子
hanoi(n-1, y, x, z); // n上面的盘子目前在y柱子,从y柱子,通过x柱子,移动到z柱子。
}
}
/**
*
* @param x 第一个柱子
* @param n 需要移动的盘子号
* @param z 第三个柱子
*/
private static void move(char x, int n, char z) {
count++;
System.out.println("第"+count+"次移动"+n+"号盘子,从"+x+"柱子到"+z+"柱子");
}
public static void main(String[] args) {
hanoi(4,'x','y','z');
}
}
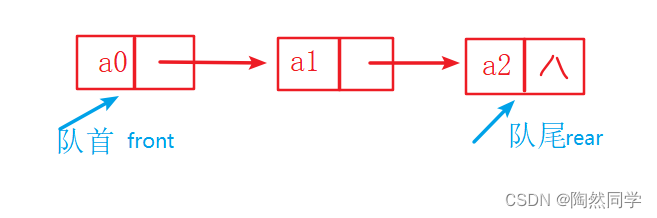
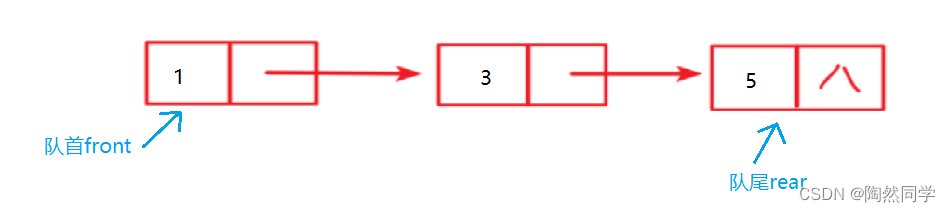
3.6 队列
3.6.1 定义
-
队列是一个特殊的线性表。
-
只允许在表尾进行插入操作
-
只允许在表头进行删除操作
-
-
队列操作特点:
-
先进先出(FIFO,First In First Out)
-
or 后进后出(LILO,Last In Last Out)
-
-
术语:
-
队尾rear:进行插入操作的一端。
-
队首front:进行删除操作的一端。
-
入队offer:进行插入操作,称为入队。
-
出队poll:进行删除操作,称为出队。
-
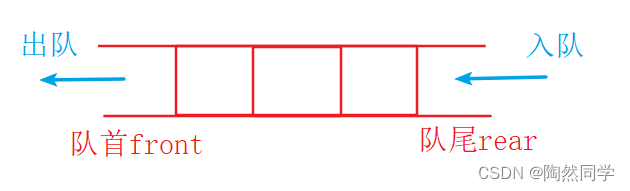
-
队列两种存储结果分类:
-
使用顺序存储的称为顺序队列
-
使用链式存储称为链队列。
-
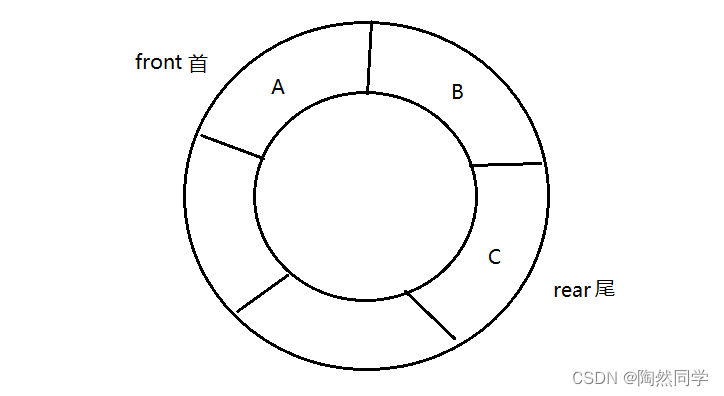
3.7 顺序队列
3.7.1 顺序队列
-
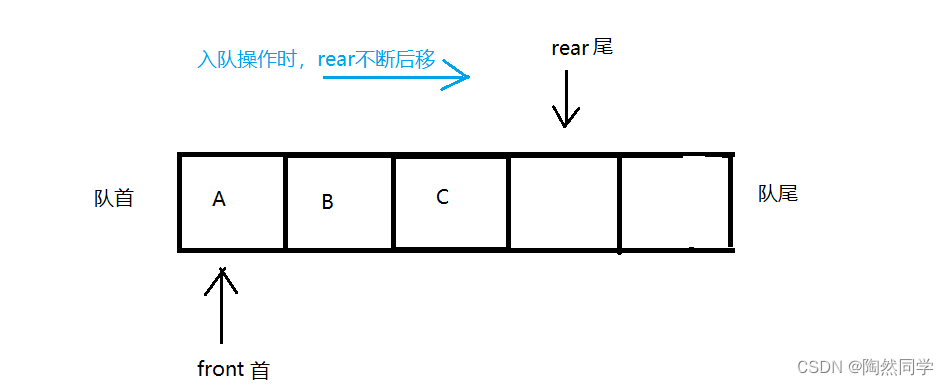
顺序队列的存储结构中,需要分配一块地址连续的存储区域来一次存放队列中从队首到队尾的所有元素。
-
操作总结:
-
front表示队首,进行出队操作时,front进行计数。
-
rear表示队尾,进行入队操作时,rear进行计数。
-
front == rear == 0 空队列。
-
-
操作步骤:
-
入队操作:

-
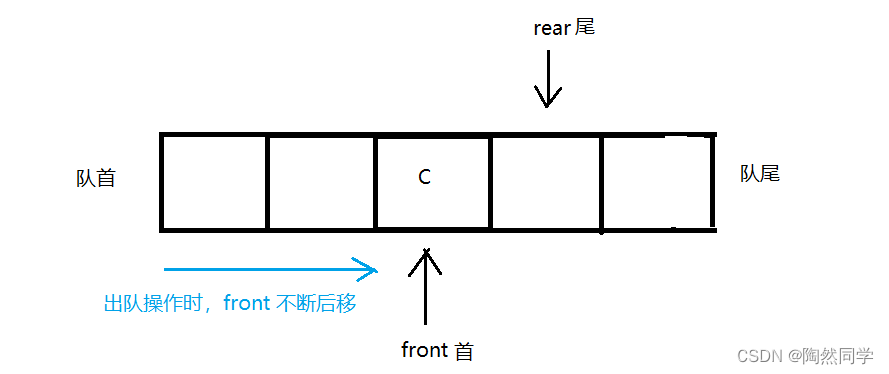
出队操作

-
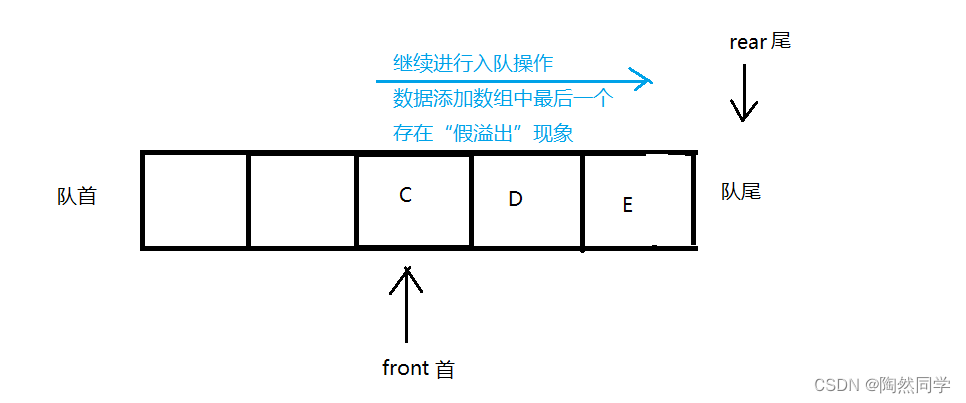
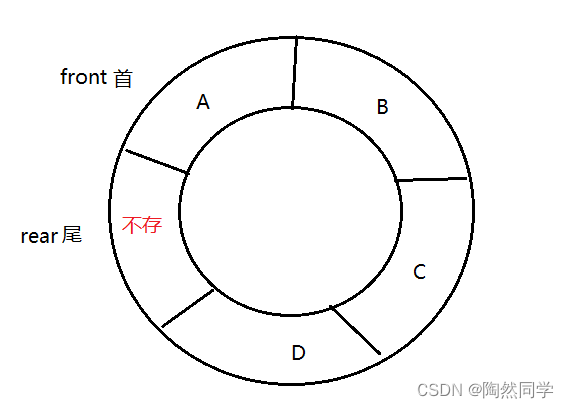
存在问题:假溢出,数组的最后一个元素已经添加数据,但队列没有满。

-
解决方案:使用
循环顺序队列解决“假溢出”问题。
-
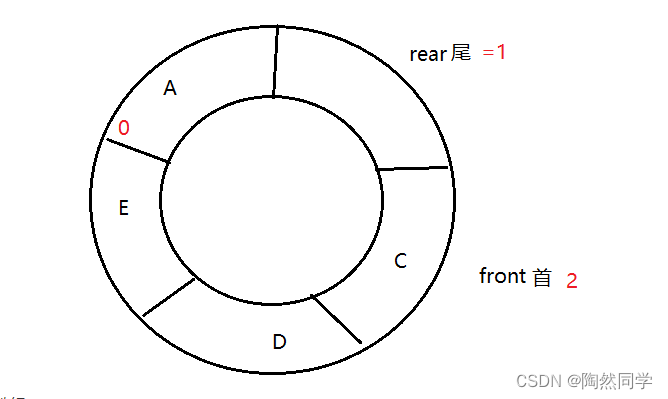
3.7.2 循环顺序队列
-
循环顺序队列:就是在逻辑上队首和队尾连接在一起。
-
存在问题:队首front和队尾rear重叠时,无法表示队列是满了,还是空的。
-
解决方案:
-
方案1:设计一个计数器(整数变量num,入队+1,出队-1,如果num=0就是空)
-
方案2:设计一个标识变量(flag=0出队,flag=1入队,重叠后0表示空,1表示满)
-
方案3:少用一个存储单位

// 队列空 front == rear; // 队列满 (rear + 1) % maxSize == front; //余数操作 5 % 5 = 0; 2 % 5 = 2;
-
3.7.3 循环顺序队列类
-
循环顺序队列,在
逻辑上是一个循环,也就是队首和队尾连接。
-
循环顺序队列,物理上就是一个数组。

public Class CircleQueue {
private Object[] queueElem; //物理数组
private int front; //队首
private int rear; //队尾
}
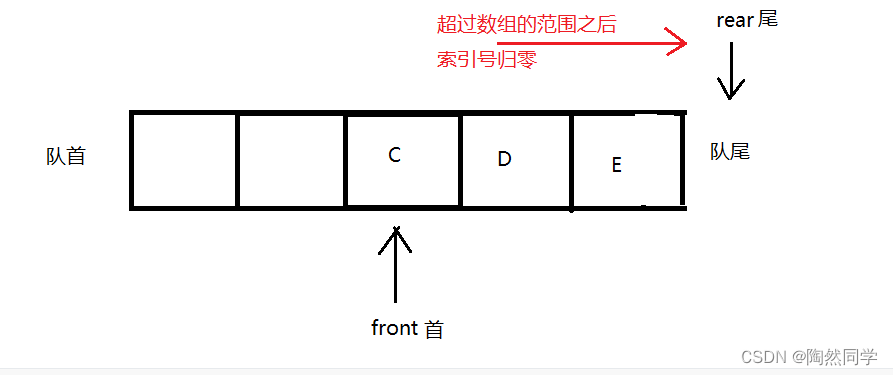
3.7.4 算法:循环顺序队列入队【重点】
public void offer(Object x) {
if( (rear+1) % queueElem.length == front ) { // 1.判断,如果已经满了,抛异常
throw new RuntimeException('队列满了');
} else {
queueElme[ rear ] = x; // 2.没有满进行入队操作
rear = (rear + 1) % queueElem.length; // 3.队尾rear累加1,但最后时需要归零
}
}
3.7.5 算法:循环顺序队列出队【重点】
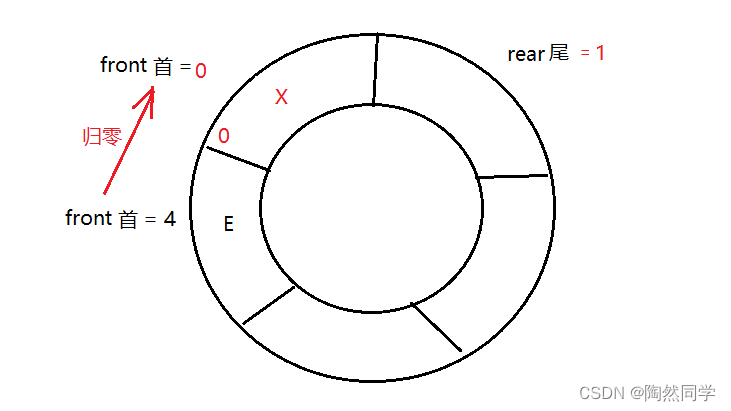
public Object poll() {
if( front == rear ) { // 判断 空 返回null
return null;
}
Object data = queueElem[front]; // 如果不为空,获得队首front元素
front = (front + 1) % queueElem.length; // 队首+1,且需要归零
return data;
}
3.8 链队列
3.8.1 定义
-
链队列:使用链式存储的队列,使用不带头结点head的单链表。
-
front结点:队首元素
-
rear结点:队尾元素

-
3.8.2 链队列类
public class LinkQueue {
private Node front; //队首(出队/删除)
private Node rear; //队尾(入队/插入)
}
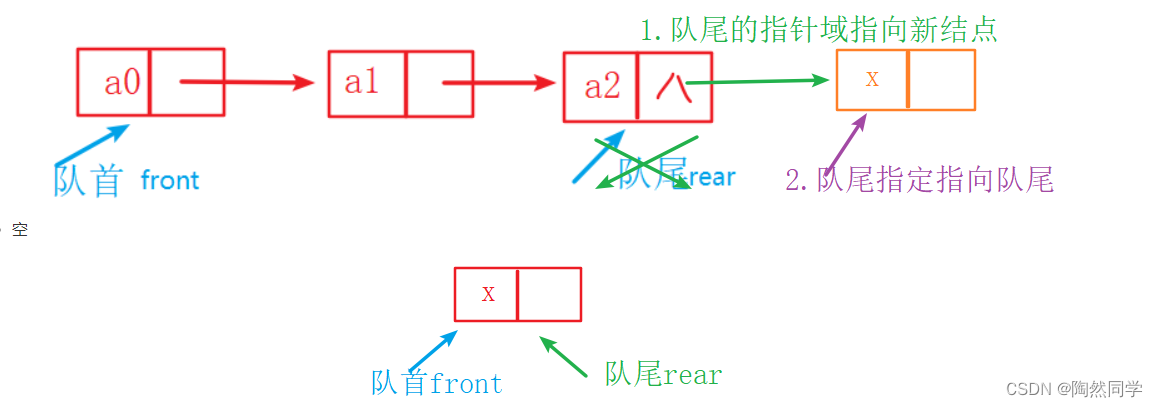
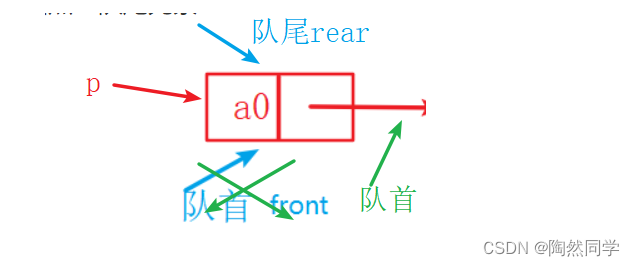
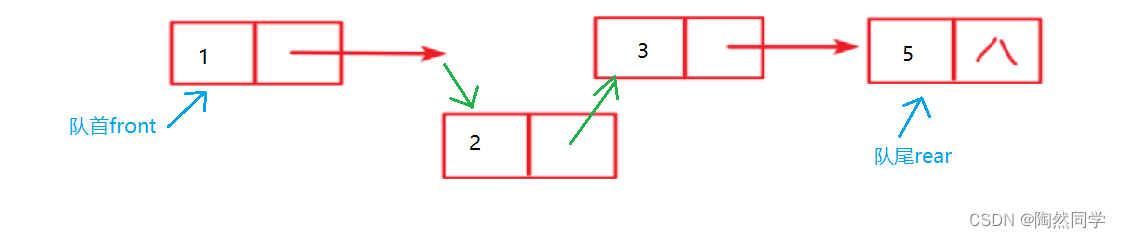
3.8.3 算法:链队列入队【重点】
-
分析:
-
非空

-
空
-
public void offer(Object x) {
Node p = new Node(x);
if(front == null) { //空
front = rear = p;
//front = p;
//rear = p;
} else { //非空
rear.next = p; //1.尾指针的指针域指向新结点
rear = p; //2.尾指针指向队尾
}
}
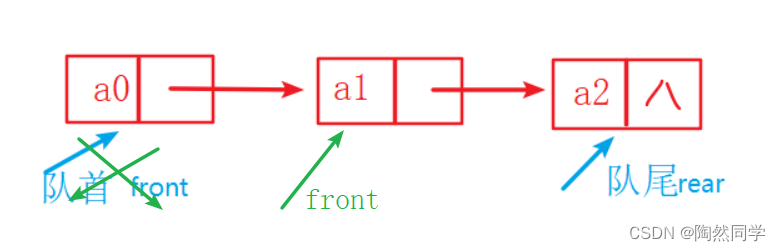
3.8.4 算法:链队列出队【重点】
-
分析:空队列、一个元素、很多元素
-
很多元素

-
一个元素:需要额外的处理队尾,将其设置成null

-
空队列:返回null即可
-
public Object poll() {
if(front != null) { //非空
Node p = front; //记录队首元素
front = front.next; //队首移动到下一个
if(p == rear) { //只有一个元素时,队首和队尾相同
rear = null; //队首已经是null,队尾也应该是null
}
return p.data; //返回之前队首元素的数据
} else { //空
return null;
}
}
3.9 优先级队列
3.9.1 定义
-
优先级队列:就是一种带优先级的队列,也就是内部需要根据
关键字的值进行排序的队列。-
与普通队列基本操作一致,队首删除。
-
区别:进行==插入==操作时,不在是队尾,对队伍中找到合适的位置。
-
-
优先级队列也可以使用两种存取方式,但常用链式存储。
-
默认队列

-
插入操作:数字小的优先级越高

-
3.9.2 优先级队列相关类
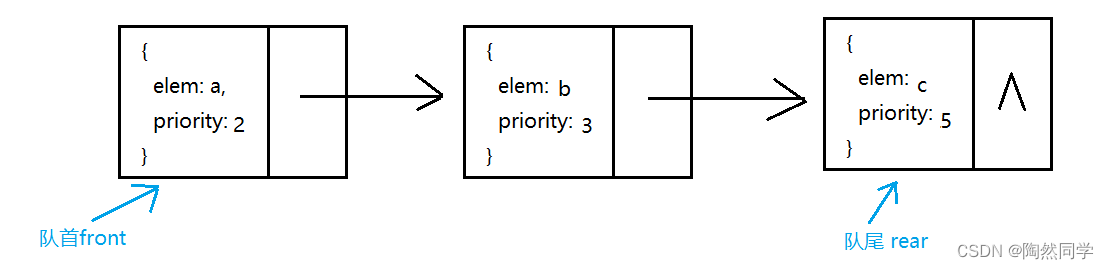
-
数据对象:数据元素的值、结点的优先级
/* { elem: a, priority: 1} */ public class PriorityData { public Object elem; //数据元素的值 public int priority; //结点的优先级 } -
队列对象
public class PriorityQueue { private Node front; //队首 private Node rear; //队尾 } -
数据之间关系
node.next //指针域 node.data //数据域,存放的数据类型是 PriorityData
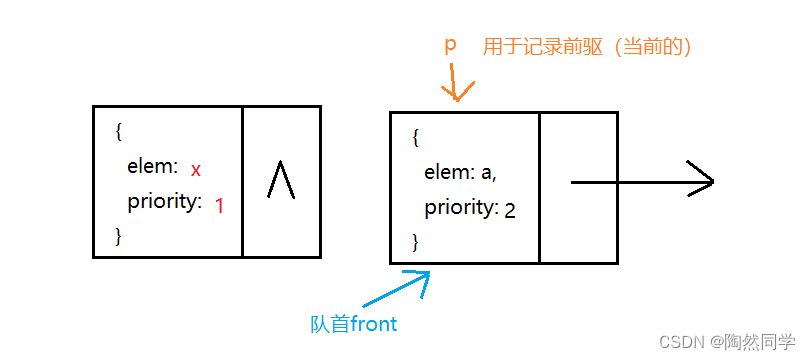
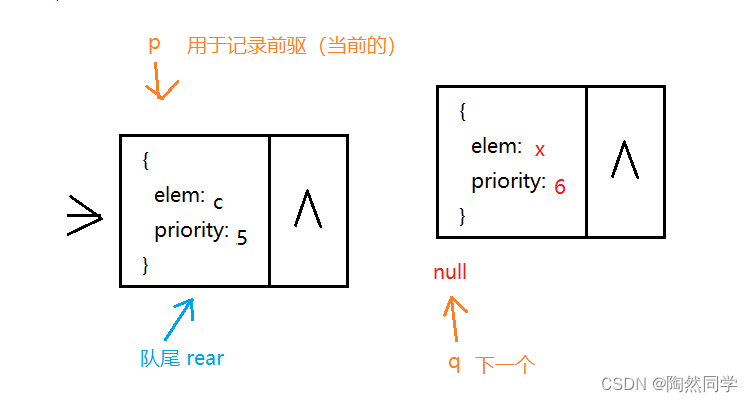
3.9.3 算法:优先级队列入队
-
需求:数字越==小==优先级越高。
-
分析:
-
前提:从队首进入,依次进行比较
-
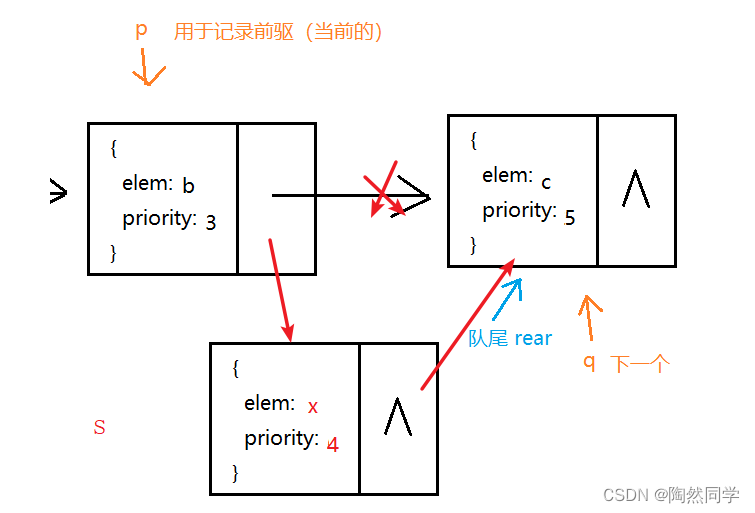
情况1:队首插入(p如果指向队首front,表示新结点优先级的数字小)

-
情况2:队尾插入 (q为null 或 p等于队尾rear)

-
情况3:剩余的中间

-
public void offer(PriorityData x) {
Node s = new Node(x); //构建新结点
// 如果空
if(front == null) { //空
front = rear = s;
} else { //非空
// 1) 移动:按照优先级进行移动,优先级大就需要继续移动
Node p = front; //用于记录前驱(之前的)
Node q = front; //用于记录下一个
while( q != null && (x.priority >= q.data.priority )) {
p = q; //记录前驱
q = p.next;
}
// 2) 插入
if(q==front) { // 2.1 队首
s.next = front; //新结点s指向队首front
front = s; //队首指针,指向队列的开始
} else if (q == null) { // 2.2 队尾
rear.next = s; //队尾指针域next,指向新结点
rear = s; //队尾指针,指向队尾
} else { // 2.3 中间
p.next = s;
s.next = q;
}
}
}
3.10 递归
3.10.1 定义
-
程序调用自身的编程技巧称为递归( recursion),由两部分组成:递推、回归。
-
递推:方法依次调用,没有返回。
-
回归:程序准备依次返回。
-
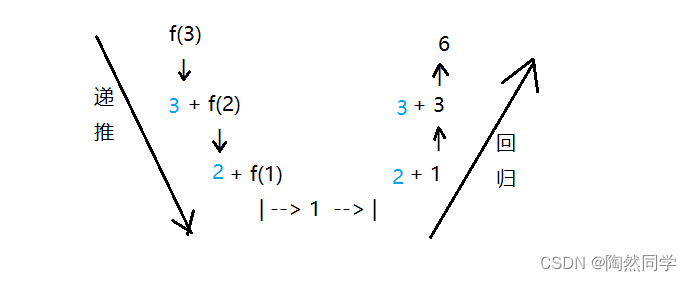
3.10.2 算法:1-n和
package recursion;
/**
* @author 桐叔
* @email liangtong@itcast.cn
*/
public class TestSum {
public static void main(String[] args) {
System.out.println(sum(10));
}
/**
* 求1-n的和
* @param n
* @return
*/
private static int sum(int n) {
if(n == 1) {
return 1;
}
return n + sum(n-1);
}
}
3.10.3 算法:n!
package recursion;
/** 测试阶乘:
* n! = 1 * 2 * 3 * 4 * .... * n
* @author 桐叔
* @email liangtong@itcast.cn
*/
public class TestFactorial {
public static void main(String[] args) {
System.out.println(factorial(4));
}
private static int factorial(int n) {
if(n == 1) {
return 1;
}
return n * factorial(n-1);
}
}
3.10.4 算法:斐波那契数列
-
定义
0、1、1、2、3、5、8、13、21、34 .... n 固定值 f(0) = 0 f(1) = 1 后面的每一项都是前两项的和 f(2) = f(0) + f(1) f(n) = f(n-1) + f(n-2)
-
算法
package recursion;
/**
* @author 桐叔
* @email liangtong@itcast.cn
*/
public class TestFibonacci {
public static void main(String[] args) {
// 斐波那契数列
for(int i = 0 ; i <= 10 ; i ++) {
System.out.print(fibonacci(i) + "、");
}
}
/**
* 计算斐波那契数列的第n项
* f(0) = 0
* f(1) = 1
* ...
* f(n) = f(n-1) + f(n-2)
* @param n
* @return
*/
private static int fibonacci(int n) {
if(n == 0) {
return 0;
}
if(n == 1) {
return 1;
}
return fibonacci(n-1) + fibonacci(n-2);
}
}
文章来源: blog.csdn.net,作者:陶然同学,版权归原作者所有,如需转载,请联系作者。
原文链接:blog.csdn.net/weixin_45481821/article/details/126794383
- 点赞
- 收藏
- 关注作者


评论(0)