【数据结构】二叉树的遍历
文章目录
5.3 二叉树的遍历
5.3.1 概述
-
二叉树的遍历:沿着某条搜索路径对二叉树中的结点进行访问,使得每个结点均被访问一次,而且仅被访问一次。“访问”的含义较为广泛,例如:输出结点信息。
-
二叉树有3条搜索路径:
-
先上后下
-
先左后右
-
先右后左
-
-
对应3条搜索路径,二叉树有7种遍历方式:
-
先上后下
-
层次遍历
-
-
先左后右 (D data根、 L left左、R right 右)
-
DLR (先根遍历、先序遍历、先根序遍历)
-
LDR (中根遍历、中序遍历、中根序遍历)
-
LRD (后根遍历、后序遍历、后根序遍历)
-
-
先右后左
-
DRL
-
RDL
-
RLD
-
-
-
需要遍历的二叉树
A
B
C
D
E
F
G
H
K
5.3.2 遍历方式【重点】
1) 层次遍历
-
若二叉树为空,则为空操作;否则,按自上而下先访问第0层的根节点,然后再从左到右依次访问各层次中的每一个结点。
-
层次遍历序列
ABECFDGHK
2)先根(序)遍历 DLR
-
若二叉树为空,则为空操作,否则
-
访问根节点
-
先根遍历左子树
-
先根遍历右子树
-

-
-
先根遍历序列
ABCDEFGHK
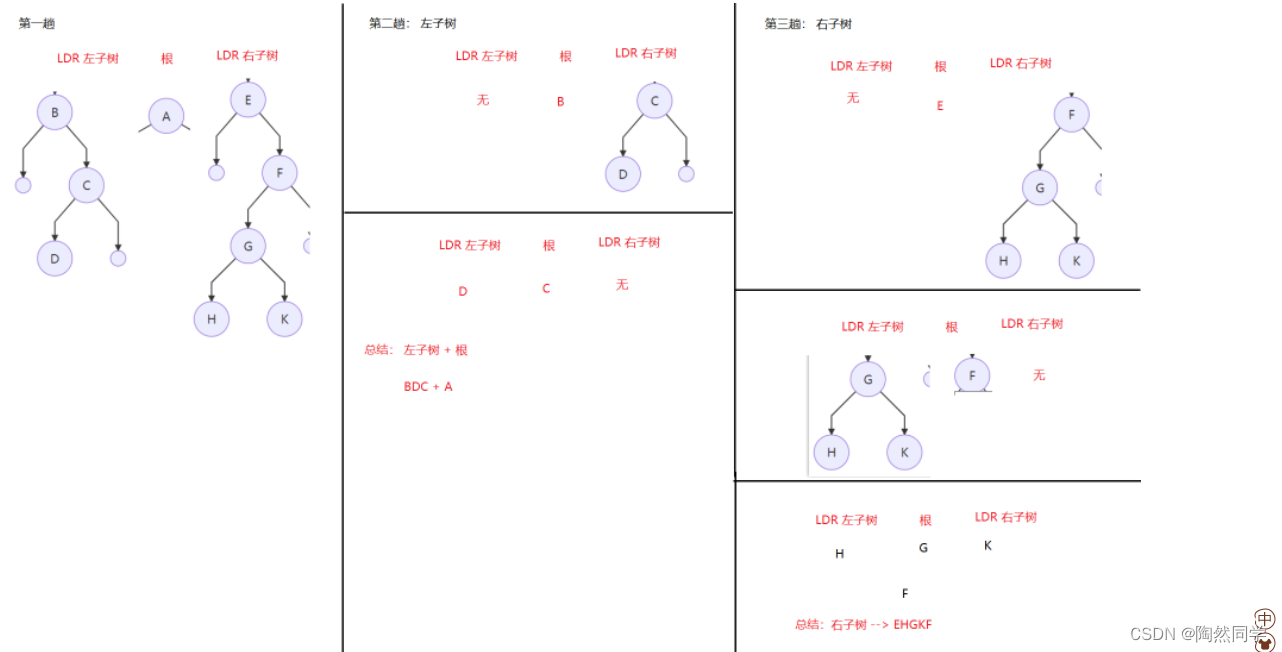
3)中根(序)遍历 LDR
-
若二叉树为空,则为空操作;否则
-
中根遍历左子树
-
访问根节点
-
中根遍历右子树
-
-
中根遍历序列
BDCAEHGKF
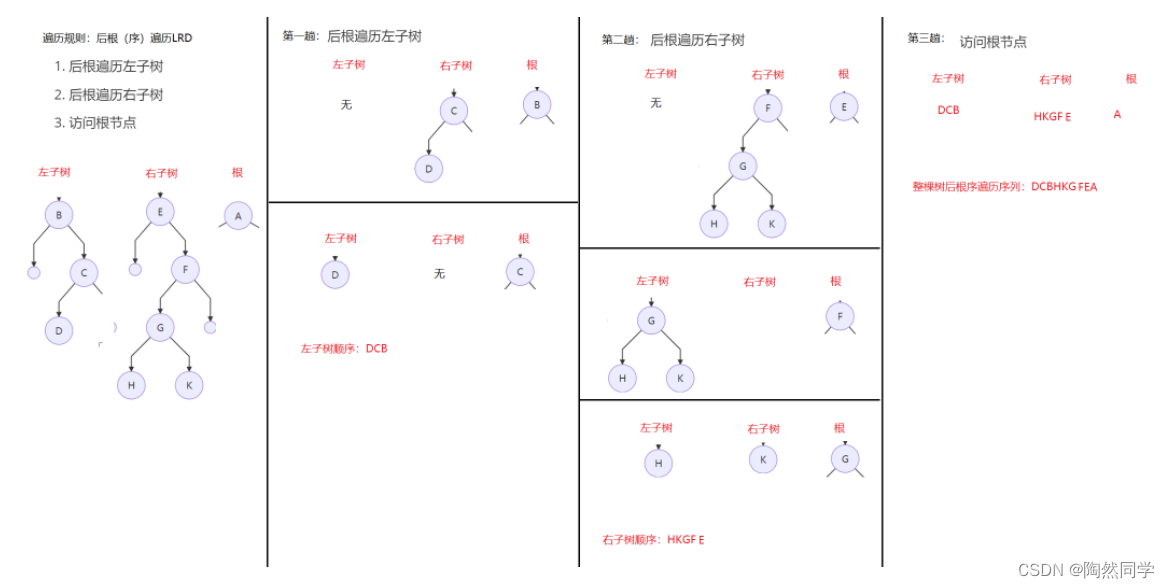
4)后根(序)遍历LRD
-
若二叉树为空,则为空操作;否则
-
后根遍历左子树
-
后根遍历右子树
-
访问根节点
-
-
后根遍历序列
DCBHKGFEA
5)练习
-
练习1:

先根序遍历:ABDEGCFH
中根序遍历:DBGEAFHC
后根序遍历:DGEBHFCA
-
练习2:

先根序遍历:ABDEGJHCFIKL
中根序遍历:DBJGEHACKILF
后根序遍历:DJGHEBKLIFCA
-
练习3:

先根序遍历:ABCDEFGHK
中根序遍历:BDCAEHGKF
后根序遍历:DCBHKGFEA
5.3.3 遍历方式:递归实现【重点】
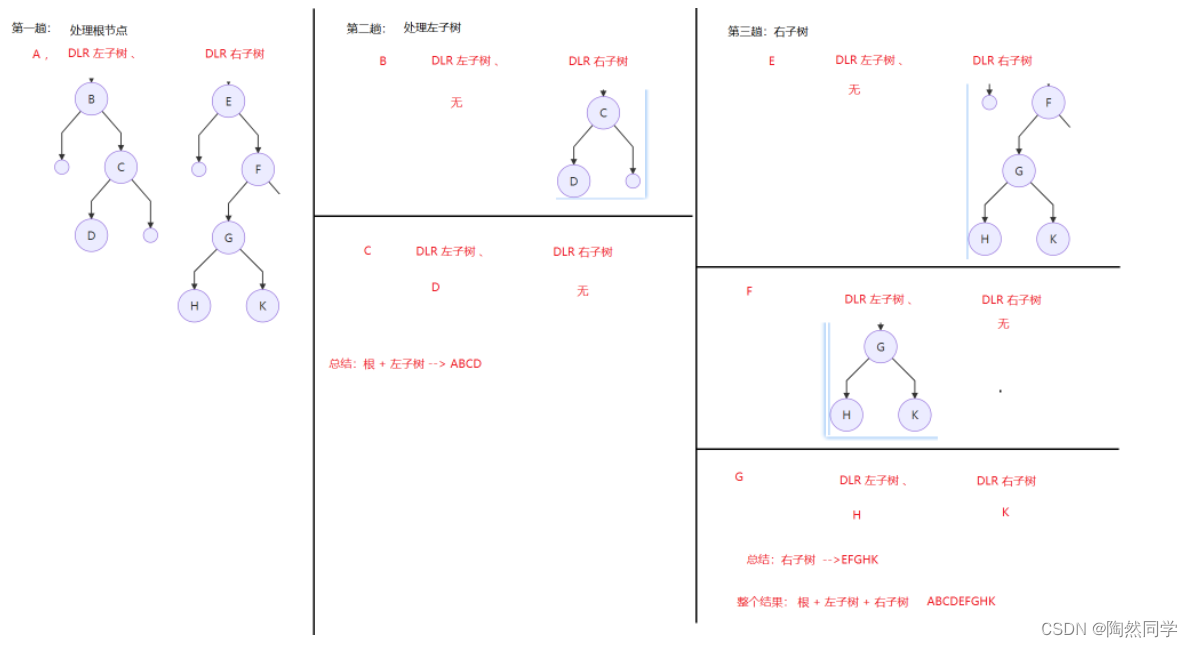
1)算法:先根(序)遍历 DLR
public void preRootTraverse(BiTreeNode T) {
if(T != null) {
System.out.print(T.data); //输出根元素
preRootTraverse(T.lchild); //先根遍历左子树
preRootTraverse(T.rchild); //先根遍历右子树
}
}
2)算法:中根(序)遍历 LDR
public void inRootTraverse(BiTreeNode T) {
if(T != null) {
inRootTraverse(T.lchild); //中根遍历处理左子树
System.out.print(T.data); //访问根节点
inRootTraverse(T.rchild); //中根遍历处理右子树
}
}
3)算法:后根(序)遍历LRD
public void postRootTraverse(BiTreeNode T) {
if(T != null) {
postRootTraverse(T.lchild); //后根遍历左子树
postRootTraverse(T.rchild); //后根遍历右子树
System.out.print(T.data); //访问根结点
}
}
4)动画演示:后根遍历
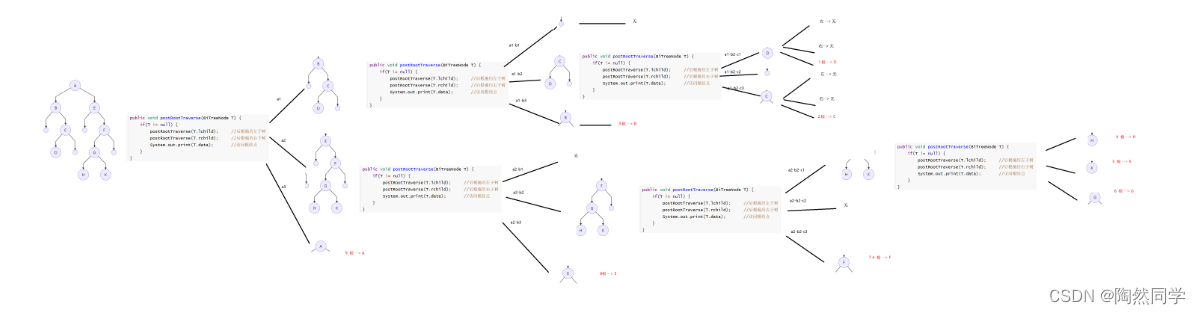
5.3.4 遍历方式:非递归实现
1)分析:先根(序)遍历 DLR
-
借助一个==栈==来记录当前被访问结点的右孩子结点,以便遍历完一个结点的左子树后,可以继续遍历该结点的右子树。
-
实现思想:
-
将根节点压栈
-
从栈顶获得需要遍历的结点A,并访问结点A。
-
此时结点A有左孩子直接访问,结点A有右孩子压入栈顶
-
同时沿着左子树继续搜索,重复步骤3
-
当左子树访问完成后,重复步骤2依次访问对应的右子树
-
2)算法:先根(序)遍历 DLR【重点】
public void preRootTraverse() {
BiTreeNode T = root;
if( T != null ) {
LinkStack S = new LinkStack(); // 创建栈记录没有访问过的右子树
S.push(T); // 将根节点压入栈顶
while(!S.isEmpty()) { // 栈中只要有数据,表示继续遍历
T = S.pop(); // 弹出栈顶数据
System.out.print(T.data); // 结点被访问
while(T != null) { // T指针,访问每一个左孩子
if(T.lchild != null) { // 输出左孩子
System.out.print(T.lchild.data);
}
if(T.rchild != null) { // 将右孩子压栈
T.push(T.rchild);
}
T = T.lchild; // 访问下一个左孩子
}
}
}
}
3)分析:中根(序)遍历 LDR
-
借助一个==栈==来记录遍历过程中所经历的而未被访问的所有结点,以便遍历完左子树后能顺利的返回到它的父节点。
-
实现思想
-
从非空二叉树的根节点出发
-
沿着该结点的左子树向下搜索,在搜索过程中将遇到的每一个结点依次压栈,直到二叉树中最左下结点压栈为止,
-
然后从栈中弹出栈顶结点并对其进行访问,访问完成后再进入该结点的右子树,
-
并用上述相同的方法去遍历该结点的右子树,直到二叉树中所有的结点都被访问。
-
4)算法:中根(序)遍历 LDR
public void inRootTraverse() {
BiTreeNode T = root;
if(T != null) {
LinkStack S = new LinkStack();
S.push(T); //将根节点压入到栈顶
while( !S.isEmpty() ) { //栈中有数据,表示遍历未完成
//1 将所有的左孩子压栈
while(S.peek() != null) { //栈顶的元素不为空,注意:不是弹栈
// 获得栈顶,
BiTreeNode temp = (BiTreeNode)S.peek();
// 并将左孩子压入栈顶
S.push(temp.lchild);
}
S.pop(); //将栈顶的空元素弹出
//2 依次弹出栈,访问当前节点,如果有右孩子继续压栈
if(! S.isEmpty()) {
T = (BiTreeNode)S.pop();
System.out.print(T.data); //访问栈顶
S.push(T.rchild);
}
}
}
}
5)分析:后根(序)遍历LRD
-
借助一个栈用记载遍历过程中所经历而未被访问的所有结点。
-
确定顶点结点是否能访问,需要知道该结点的右子树是否被遍历完成。
-
引入两个变量,一个访问标记变量flag和一个结点指针p
-
flag永不标记当前栈顶结点是否被访问
-
p指向当前遍历过程中最后一个被访问的结点。
-
-
-
实现思想
-
从非空二叉树的根节点出发
-
将所有的左孩子相继压栈,
-
然后获得栈中每个结点A,如果该结点A没有右孩子或右孩子已经访问过,将访问结点A
-
如果结点A有右孩子或右孩子未被访问过,继续压栈
-
通过标记,使程序开始出了新添加进入的结点。
-
6)算法:后根(序)遍历LRD
public void postRootTraverse() {
BiTreeNode T = root;
if( T != null) {
LinkStack S = new LinkStack();
S.push(T);
// 声明两个变量
Boolean flag; //用于记录是否被访问
BiTreeNode p; //用于记录上一次处理的结点
while(! S.isEmpty() ) {
//1 将所有的左孩子压栈
while(S.peek() != null) { //栈顶的元素不为空,注意:不是弹栈
// 获得栈顶,
BiTreeNode temp = (BiTreeNode)S.peek();
// 并将左孩子压入栈顶
S.push(temp.lchild);
}
S.pop(); //将栈顶的空元素弹出
while( !S.isEmpty() ) {
T = (BiTreeNode) S.peek();
if(T.rchild == null || T.rchild == p) { // 没有右孩子 或 已经访问过
System.out.print(T.data);
S.pop(); //弹出
p = T; //记录刚才访问过的
flag = true; //没有新元素,继续访问
} else {
S.push(T.rchlid);
flag = false; //新右子树添加
}
if(!flag) {
break; //如果有右子树,需要重新开始
}
}
}
}
}文章来源: blog.csdn.net,作者:陶然同学,版权归原作者所有,如需转载,请联系作者。
原文链接:blog.csdn.net/weixin_45481821/article/details/126794643
- 点赞
- 收藏
- 关注作者




评论(0)