【数字信号去噪】基于matlab麻雀算法优化VMD信号去噪(目标函数为包络熵局部极小值)【含Matlab源码 2111期】

一、鲸鱼算法优化VMD信号去噪简介

1 VMD算法
VMD(variational mode decomposition)是一种将信号非递归分解成数个具有准正交性的带限本征模态函数的算法，其基本原理可以表示为一个约束变分问题的求解，构造的约束变分问题表示为

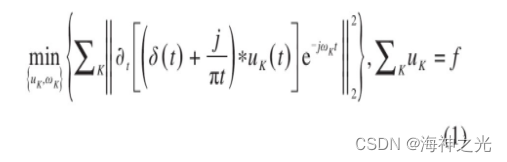
式中：uK为VMD分解后的第K个IMF分量；ωK为第K个IMF分量的瞬时频率；δ(t)为狄拉克函数；∗为卷积符号；

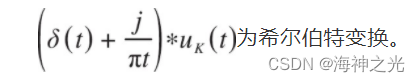
引入二次惩罚因子α和拉格朗日乘子λ使变分问题不受约束，构造的增广拉格朗日函数如下：

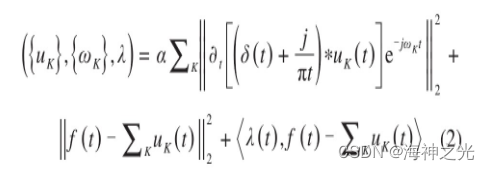
采用乘子交替方向算法交替更新得到K个IMF及其对应的中心频率。

从式(2)可以看出：K和α影响着VMD的分解性能。若设置的K较小，则信号的多个分量可能同时包含在1个模态中；若K较大，则会导致1个分量包含在多个模态中，迭代得到的中心频率也会重叠。对α而言，若α很大，则带宽限制就会很窄，从而导致有用的频率成分被消除；反之，冗余频率成分将会被保留下来。因此，本文提出鲸鱼优化算法来优化确定最佳参数组合(K，α)。

2 麻雀搜索算法
SSA算法是Xue等于2020年提出的一种新的优化算法，可以概括为寻找-跟随-预警的抽象模型，它模拟了麻雀的觅食过程以获取待优化问题的解。

设M是麻雀觅食的优化搜索空间集，存在N只麻雀个体，第x只麻雀处在M集的位置表示为Sx=[sx1,⋯,sxd,sx M],x=1,2,3,⋯,N,sxd表示麻雀x在M集中居d维的位置，寻找者位置更新表达式为：

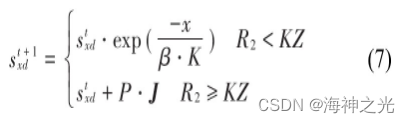
其中：t为当前迭代数；K为最大迭代数；β是属于区间(0,1]的均匀随机数；P是服从N(0,1)分布的随机数；J为1×d的单位矩阵；R2∈[0,1]为预警值，KZ∈[0.5,1]为安全值。而跟随者位置更新可表达为：

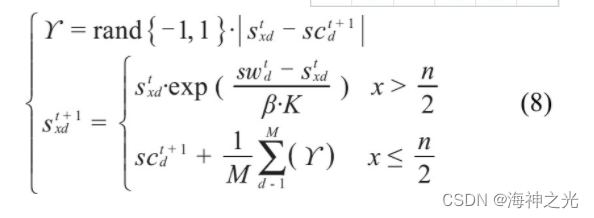
式中：swdt为麻雀群进行t次迭代时处在d维最差的位置；反之scdt+1为t+1次迭代时最好的位置；当x>n/2，表示适应度较低，需扩大搜索范围；当x≤n/2时，表示适应度较高，可在sc位置周围随机觅食。预警麻雀位置迭代为：

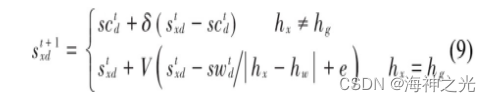
式中：δ为服从N (0,1)的随机数；V为[-1,1]的随机数，表示麻雀移动的方向，同时控制步长；e是避免分母为零而设的极小值；hx为处于位置x时麻雀的适应度值，hw为当前麻雀的最差适应度值，hg则为最优值。通常，预警麻雀个数占总种群的15%，为兼顾优化准确性和计算效率，本文设置种群数和最大迭代数[N,M]=[30,20]。

在对VMD的k、α进行优化时，需考虑SSA算法中一关键点，即适应度函数值的构建。本文选取包络熵为麻雀优化算法的适应度函数值，包络熵可以很好评价信号的稀疏性，反映所研究信号分解情况的概率分布特性。

二、部分源代码

clc
clear
close all
addpath(‘toolf’)
warning off

% 读取数据
[file,path,indx] = uigetfile({’.xlsx’;’.xls’;’.txt’;’.*’},‘File Selector’);
if indx == 1||indx==2
data=xlsread(strcat(path, file));
elseif indx == 3
data=load(strcat(path, file));
else
warning(‘请选择数据集进行实验’);
return;
end

%采样频率
fs=12800;
% 读取前1000长度的信号
len=1000;
s=data(1:len);
% 采样时间
t = (0:len-1)/fs;

%% 设定麻雀搜索算法参数
popsize =6; % 种群大小
iter = 30; % 最大迭代次数
dim = 2; % 变量个数
lb = [100 3]; % alpha范围 K范围 下限
ub = [2000 7]; % 上限

%% 麻雀搜索算法SSA优化VMD参数

tic , % 开始计时

SSA_VMD(popsize,iter,dim,lb,ub,0); % 0表示不保存IMF，1，导出IMF并保存

toc, % 结束计时

三、运行结果

四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1]褚惟,王贵勇,刘韬,王振亚.麻雀算法参数优化VMD联合K-SVD滚动轴承故障诊断[J].噪声与振动控制. 2022,42(04)

3 备注
简介此部分摘自互联网，仅供参考，若侵权，联系删除

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/126803747