puzzle(025)多米诺骨牌
目录
38多米诺骨牌(3)53(4)68(5)81(6)94(7)
106 多米诺骨牌(12)119(8)130(9)142(10)150(11)
数邻
找出棋盘上所有的相邻数对。每两个数字组成的数对只能出现一次。
4*5
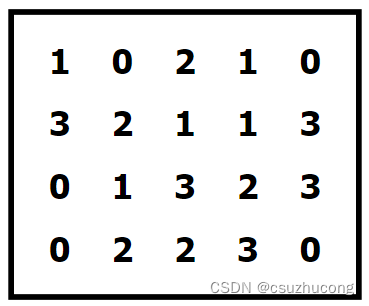

5*6


6*7

首先很容易推出 (2,2)


智力游戏 多米诺骨牌
智力游戏中的关卡。
11多米诺骨牌(1)

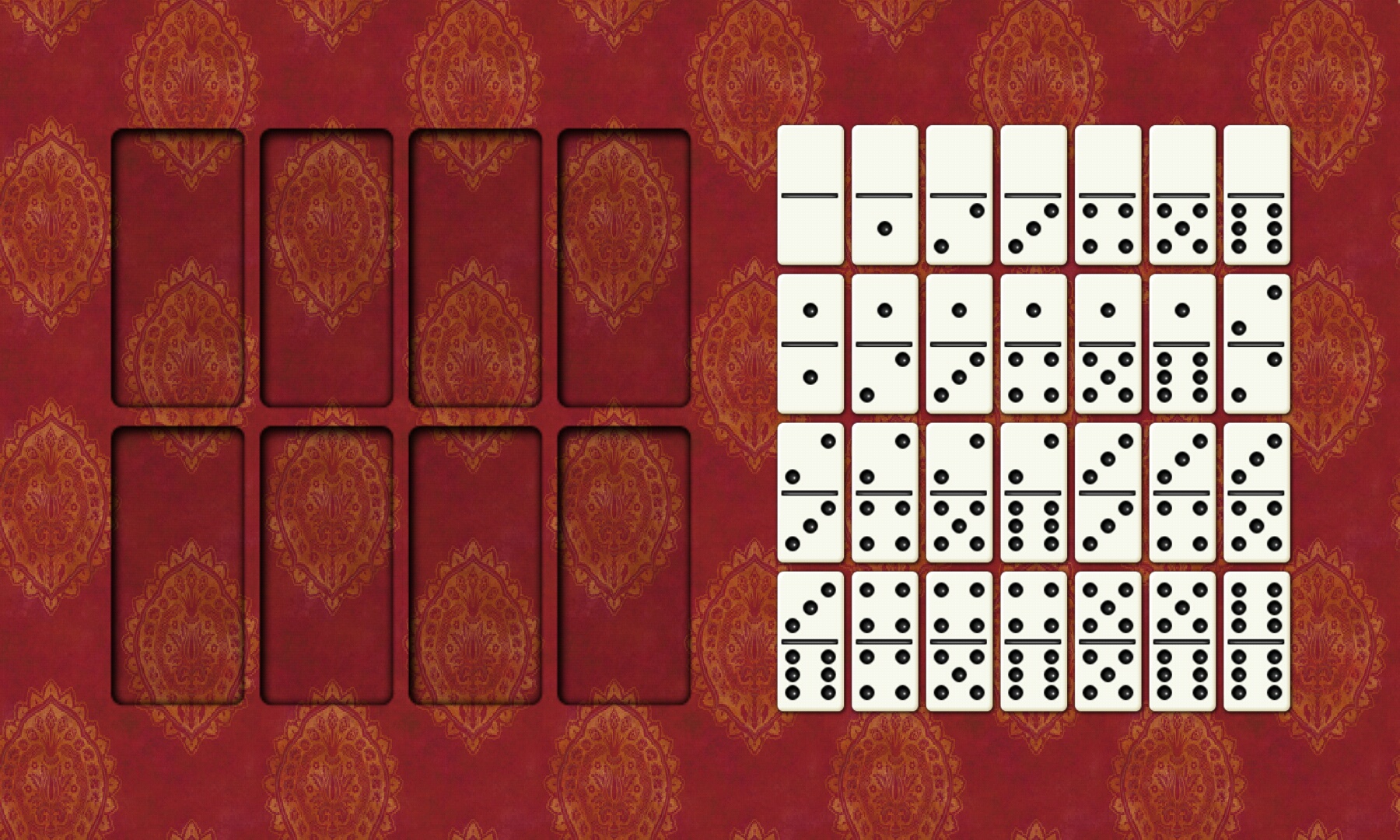
这个是4*4的多米诺骨牌,规则类似幻方。
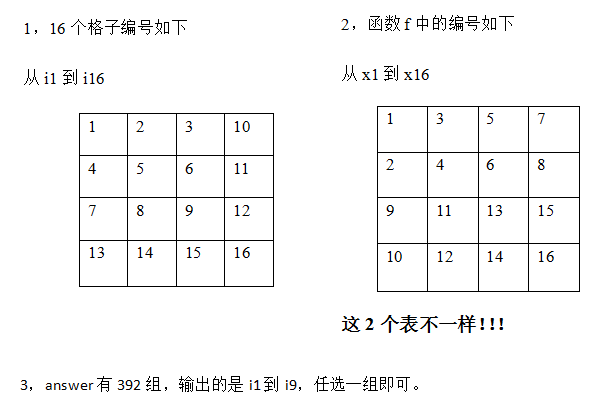
代码:
-
#include<iostream>
-
using namespace std;
-
-
int ifsame(int a, int b, int c, int d)//判断(a,b)和(c,d)是否相同
-
{
-
if (a == c && b == d || a == d && b == c)return 1;
-
return 0;
-
}
-
-
int f(int x1, int x2, int x3, int x4, int x5, int x6, int x7, int x8, int x9, int x10, int x11, int x12, int x13, int x14, int x15, int x16)
-
判断这8组有没有相同的
-
{
-
int shuzu[16] = { x1, x2, x3, x4, x5, x6, x7, x8, x9, x10, x11, x12, x13, x14, x15, x16 };
-
for (int i = 0; i < 16; i += 2)for (int j = i + 2; j < 16; j += 2)
-
if (ifsame(shuzu[i], shuzu[i + 1], shuzu[j], shuzu[j + 1]))return 0;
-
return 1;
-
}
-
-
int main()
-
{
-
cout << "answer:" << endl;
-
int n = 1;
-
for (int i1 = 0; i1 < 7; i1++)for (int i2 = 0; i2 <= 6 - i1; i2++)for (int i3 = 0; i3 <= 6 - i1 - i2; i3++)
-
for (int i4 = 0; i4 <= 6 - i1; i4++)for (int i5 = 0; i5 <= 6 - i4; i5++)
-
for (int i6 = 0; i6 <= 6 - i4 - i5; i6++)for (int i7 = 0; i7 <= 6 - i1 - i4; i7++)
-
{
-
int i8 = i1 + i1 + i2 + i3 + i4 - i6 + i7 - 6;
-
int temp = 18 - i1 - i1 - i2 - i3 - i4 - i5 - i5 - i6 - i7 - i8;
-
if (temp % 2 == 0 && i8 >= 0 && temp >= 0)
-
{
-
int i9 = temp / 2, i10 = 6 - i1 - i2 - i3, i11 = 6 - i4 - i5 - i6, i12 = 6 - i7 - i8 - i9;
-
int i13 = 6 - i1 - i4 - i7, i14 = 6 - i2 - i5 - i8, i15 = 6 - i3 - i6 - i9, i16 = 6 - i1 - i5 - i9;
-
if (i14 >= 0 && i12 >= 0 && i15 >= 0 && i16 >= 0)if (f(i1, i4, i2, i5, i3, i6, i10, i11, i7, i13, i8, i14, i9, i15, i12, i16))
-
cout << n++ << " " << i1 << " " << i2 << " " << i3 << " " << i4 << " " << i5 << " " << i6 << " " << i7 << " " << i8 << " " << i9 << endl;
-
}
-
}
-
cout << "一共有" << n-1 << "组";
-
system("pause > nul");
-
return 0;
-
}
结果:

23多米诺骨牌(2)

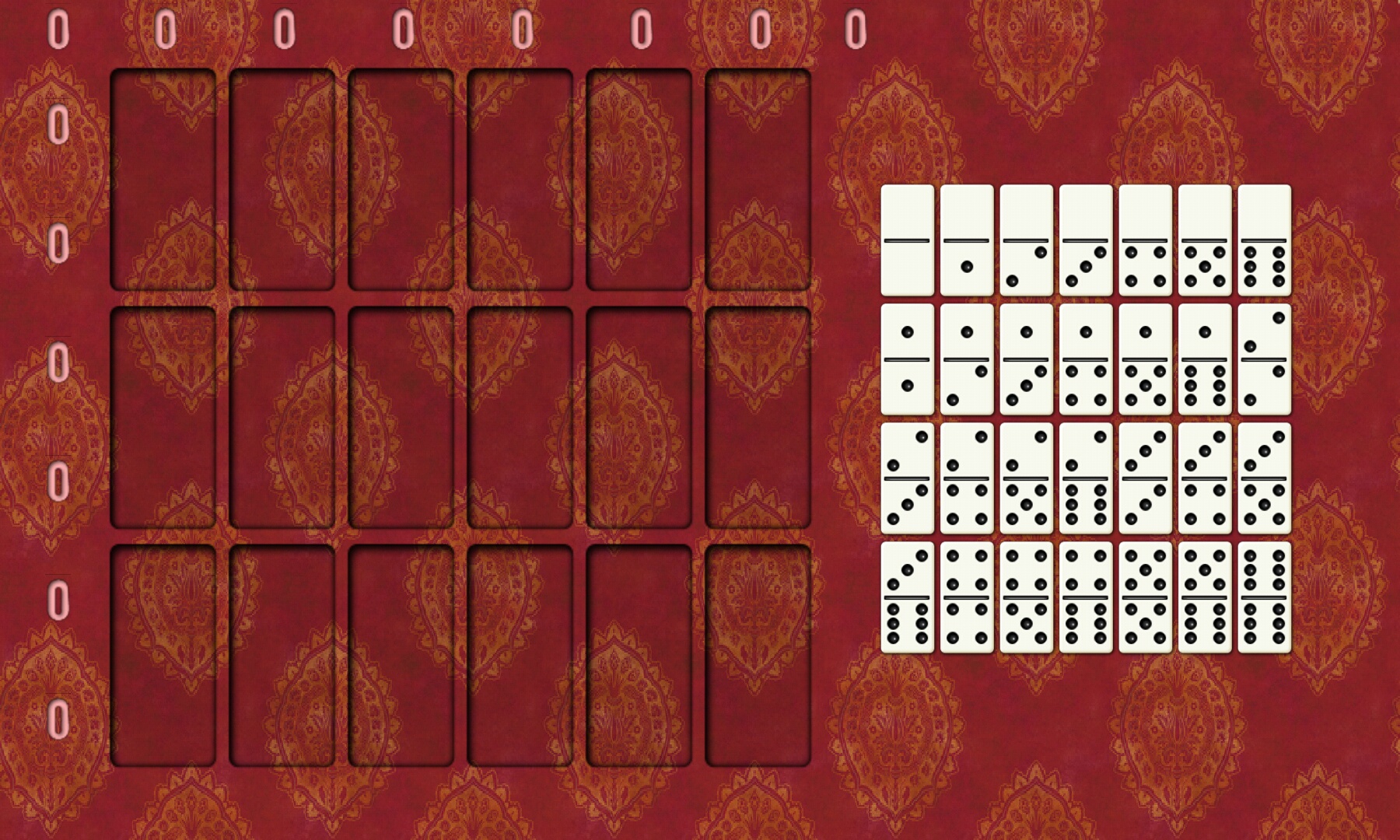
多米诺骨牌问题都可以大致分成2大步
第一步,让每一行每一列的和符合要求
第二步,仅仅通过调整行和列的顺序,使得对角线也符合要求
第一步是肯定可以实现的,但是实现了第一步之后,能否继续实现第二步就不一定了。
第一步,要使每行每列以及两对角线的和均为13
注意到,28块每块的2个数之和分别为012233444555,666677788899,10,10,11,12
其中任意18块的和最小为76
现在要找出18块,和为78,因为和76隔的不多,所以肯定有一些规律可循。
最后的结果是:01223344455666必选,剩余的4块只有4种情况,分别为6777,5688,5679,5778
将18个数字分成6组(对应着6列),每组的和都是13,可以手算出来所有的情况:
012233444556666777有3种分组方法
067 166 247 256 337 445
067 166 247 247 355 346
067 157 247 256 346 346
012233444555666688有1种分组方法
058 148 256 256 346 346
012233444555666679有5种分组方法
067 139 256 256 346 445
049 157 256 256 346 346
049 166 256 256 337 445
067 166 229 346 355 445
049 166 247 256 346 355
012233444555666778有7种分组方法
058 157 247 256 346 346
067 157 256 238 346 445
067 148 256 256 337 445
058 166 247 256 337 445
067 148 247 256 346 355
067 166 238 247 355 445
058 166 247 247 346 355
然后将18个数字分成3组(对应着3大行),上面显示的每3个连续的数都分别出现在不同的组中,每组的和都是26
这个自己试试就能解决,也可以编程求出所有的解,毕竟不一定所有的情况都能顺利完成第二步。
分组代码:
-
#include<iostream>
-
using namespace std;
-
-
int change(int n) //将3位数abc换成cab
-
{
-
int c = n % 10;
-
int ab = n / 10;
-
return ab + c * 100;
-
}
-
-
int main()
-
{
-
int num[6], nu[6]; //nu的作用是把abc换成acb
-
int number[6][6]; //number的一行就是abc,cab,bca,acb,bac,cba
-
//如果abc3个数字有重复的,只要让nu为0,那么后面3个就都是0,这么做是为了避免输出重复
-
//而且还可以减少一些重复计算
-
int sum36 = 0; //sum36是输入的18个数码的和,也就是36个点数之和
-
for (int i = 0; i < 6; i++)
-
{
-
cin >> num[i]; sum36 += num[i] / 100 + (num[i] / 10) % 10 + num[i] % 10;
-
int c = num[i] % 10;
-
int ab = num[i] / 10;
-
nu[i] = ab * 10 - ab % 10 * 9 + c * 10;
-
if (nu[i] == num[i] || nu[i] == change(num[i]) || nu[i] == change(change(num[i])))
-
nu[i] = 0;//判断abc3个字母有没有重复的
-
number[i][0] = num[i]; number[i][3] = nu[i];
-
for (int j = 0; j < 5; j++)if (j != 2)
-
number[i][j + 1] = change(number[i][j]);
-
}
-
sum36 /= 3;
-
int n1, n2, n3, n4, n5, n6, sum;
-
for (int j1 = 0; j1 < 6; j1++)if (number[1][j1])
-
for (int j2 = 0; j2 < 6; j2++)if (number[2][j2])
-
for (int j3 = 0; j3 < 6; j3++)if (number[3][j3])
-
for (int j4 = 0; j4 < 6; j4++)if (number[4][j4])
-
for (int j5 = 0; j5 < 6; j5++)if (number[5][j5])
-
for (int j6 = 0; j6 < 6; j6++)if (number[0][j6])
-
{
-
n1 = number[1][j1], n2 = number[2][j2], n3 = number[3][j3];
-
n4 = number[4][j4], n5 = number[5][j5], n6 = number[0][j6];
-
sum = n1 + n2 + n3 + n4 + n5 + n6;
-
if (sum != sum36 * 111)continue;
-
if ((n1 % 10 + n2 % 10 + n3 % 10 + n4 % 10 + n5 % 10 + n6 % 10) != sum36)continue;
-
printf("%03d,%03d,%03d,%03d,%03d,%03d\n", n1, n2, n3, n4, n5, n6);
-
}
-
cout << "end§";
-
system("pause>nul");
-
return 0;
-
}
输入:067 166 247 256 337 445
输出:
166,247,625,733,445,670
166,247,526,733,544,670
166,247,526,733,454,760
166,724,562,373,454,607
......
661,742,625,337,445,076
661,742,625,337,454,067
661,742,526,337,544,076
end§
这样,任选一行就可以完成差不多第一步了。
比如,我就选第一行:166,247,625,733,445,670
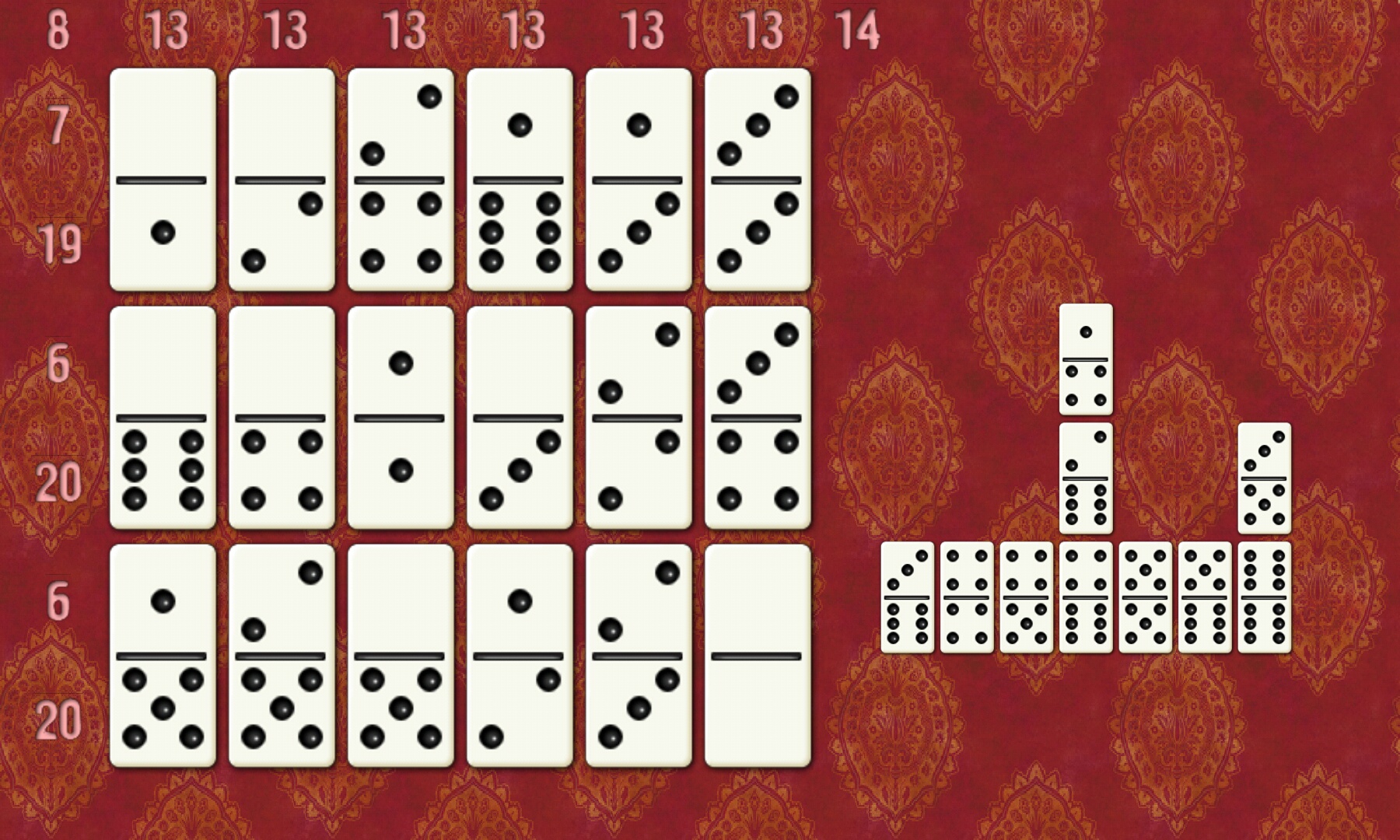
最后一小步是把某些块上下倒置,使得每一行的和都为13
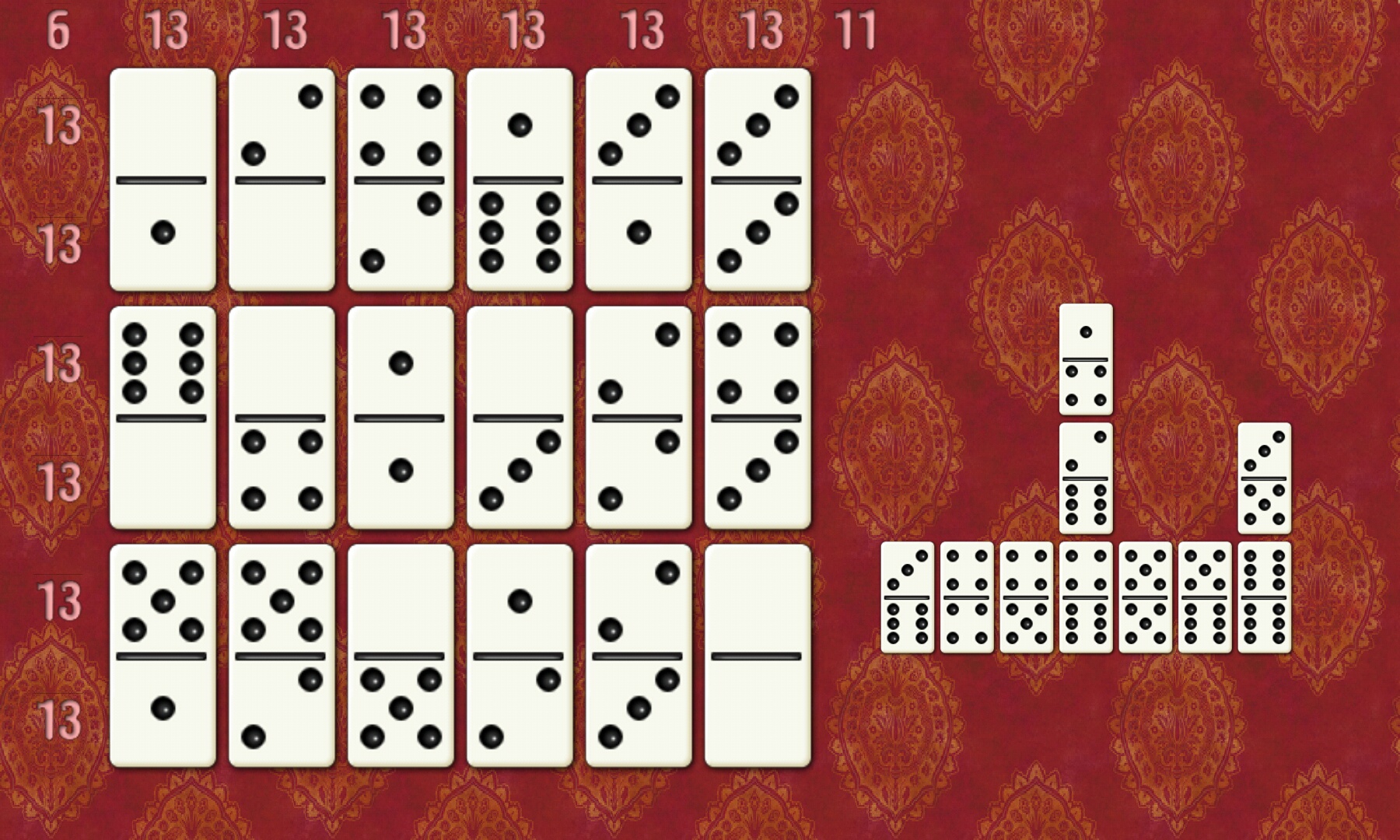
第二步,仅仅通过调整行和列的顺序,使得对角线的和也为13
这个手动实现比较麻烦,但是编程却比较容易,无法就是枚举各种顺序
把上图中的36个数字硬编码到数组num中,运行即可得到答案
代码:
-
#include<iostream>
-
using namespace std;
-
-
int num[6][6]=
-
{0,2,4,1,3,3,
-
1,0,2,6,1,3,
-
6,0,1,0,2,4,
-
0,4,1,3,2,3,
-
5,5,0,1,2,0,
-
1,2,5,2,3,0
-
}
-
;需要硬编码进来
-
-
void change_column(int j1, int j2) //把这2列的数据交换
-
{
-
for (int i = 0; i < 6; i++)
-
{
-
int temp = num[i][j1];
-
num[i][j1] = num[i][j2];
-
num[i][j2] = temp;
-
}
-
}
-
-
void change_row(int i1, int i2) //把这2行的数据交换
-
//这个函数除了在choose中调用外,只能被调用成change_row(0,1)、change_row(2,3)、change_row(4,5)三种
-
//而且由于对称性,change_row(2,3)是不需要调用的
-
{
-
for (int j = 0; j < 6; j++)
-
{
-
int temp = num[i1][j];
-
num[i1][j] = num[i2][j];
-
num[i2][j] = temp;
-
}
-
}
-
-
void choose(int i) //这个函数只能被调用成choose(0)、choose(2)、choose(4)三种情况
-
{
-
change_row(i, 2);
-
change_row(i + 1, 3);
-
}
-
-
bool ok(int sum) //检查2条对角线的和是否和1列的和相同
-
{
-
int t = 0;
-
for (int i = 0; i < 6; i++)t += num[i][i];
-
if (t != sum)return false;
-
t = 0;
-
for (int i = 0; i < 6; i++)t += num[i][5 - i];
-
if (t != sum)return false;
-
return true;
-
}
-
-
int out()
-
{
-
for (int i = 0; i < 6; i++)
-
{
-
for (int j = 0; j < 6; j++)cout << num[i][j] << " ";
-
cout << endl;
-
}
-
system("pause>nul");
-
return 0;
-
}
-
-
int main()
-
{
-
int sum = 0;
-
for (int i = 0; i < 6; i++)sum += num[i][0];
-
for (int i = 0; i < 6; i++)
-
{
-
change_column(0, i);
-
for (int i = 1; i < 6; i++)
-
{
-
change_column(1, i);
-
for (int i = 2; i < 6; i++)
-
{
-
change_column(2, i);
-
for (int i = 3; i < 6; i++)
-
{
-
change_column(3, i);
-
for (int i = 4; i < 6; i++)
-
{
-
change_column(4, i);
-
for (int i = 5; i < 6; i++)
-
{
-
change_column(5, i);
-
for (int i = 0; i < 6; i += 2)
-
{
-
choose(i);
-
if (ok(sum))return out();
-
change_row(4, 5);
-
if (ok(sum))return out();
-
change_row(0, 1);
-
if (ok(sum))return out();
-
}
-
}
-
}
-
}
-
}
-
}
-
}
-
}
输出:
6 2 1 0 4 0
0 2 1 3 3 4
5 2 0 1 0 5
1 3 5 2 0 2
0 3 4 1 3 2
1 1 2 6 3 0
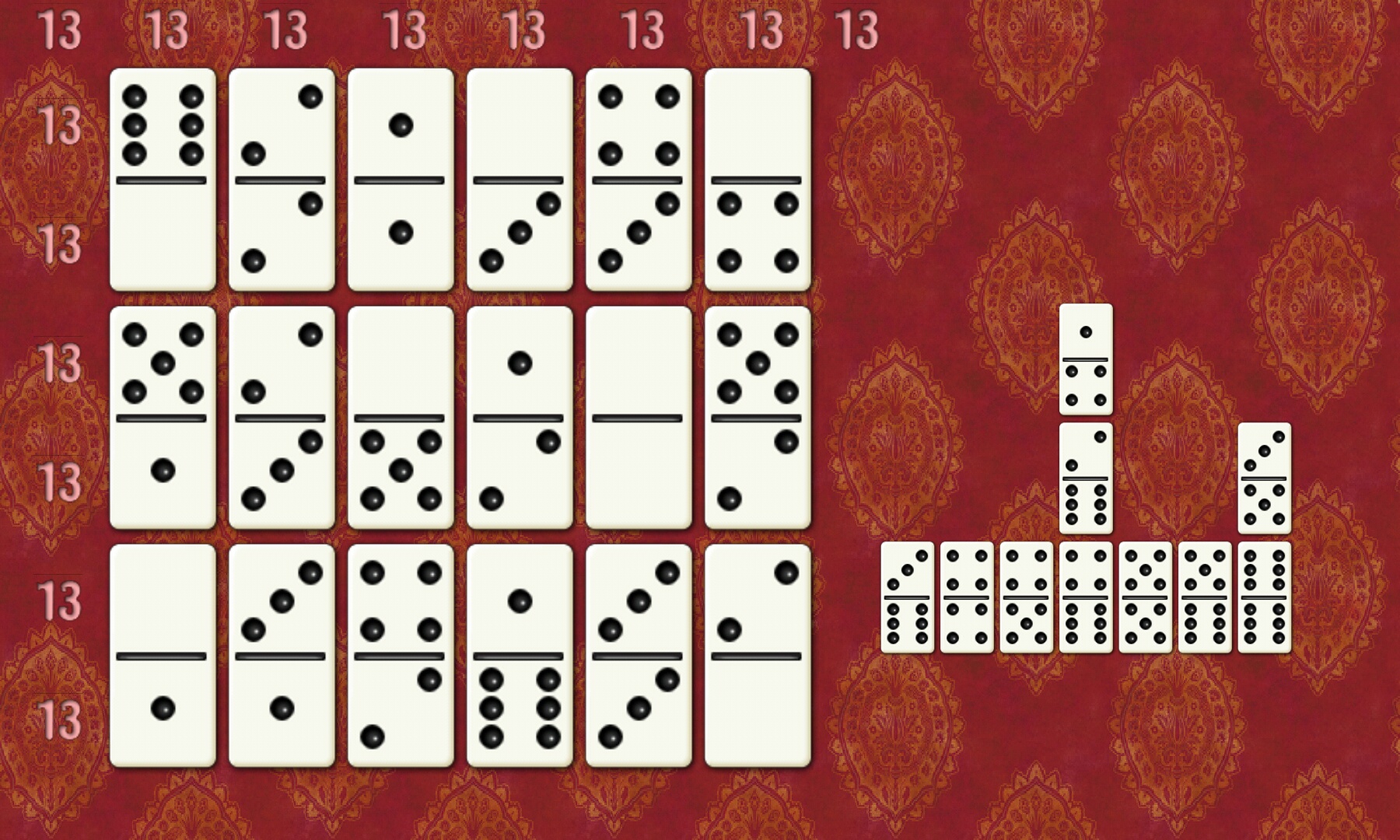
这样便过关了。
38多米诺骨牌(3)53(4)68(5)81(6)94(7)
这5关规则都和23多米诺骨牌(2)一样,所以方法也是一样:
第一步,让每一行每一列的和符合要求
第二步,仅仅通过调整行和列的顺序,使得对角线也符合要求
不过数字和分别变成了14、15、16、17、18
这样,就很容易完成第一步,基本上不会遇到障碍,这一点和和为13的情况是不一样的。
这就好像用2个骰子丢出和为2的2个数字很难,但是丢出和为7的2个数字就很容易,道理是一样的。
所以,这4关,我都是直接完成第一步,没有障碍,然后运行23多米诺骨牌(2)里面的代码完成第二步即可。
38多米诺骨牌(3)
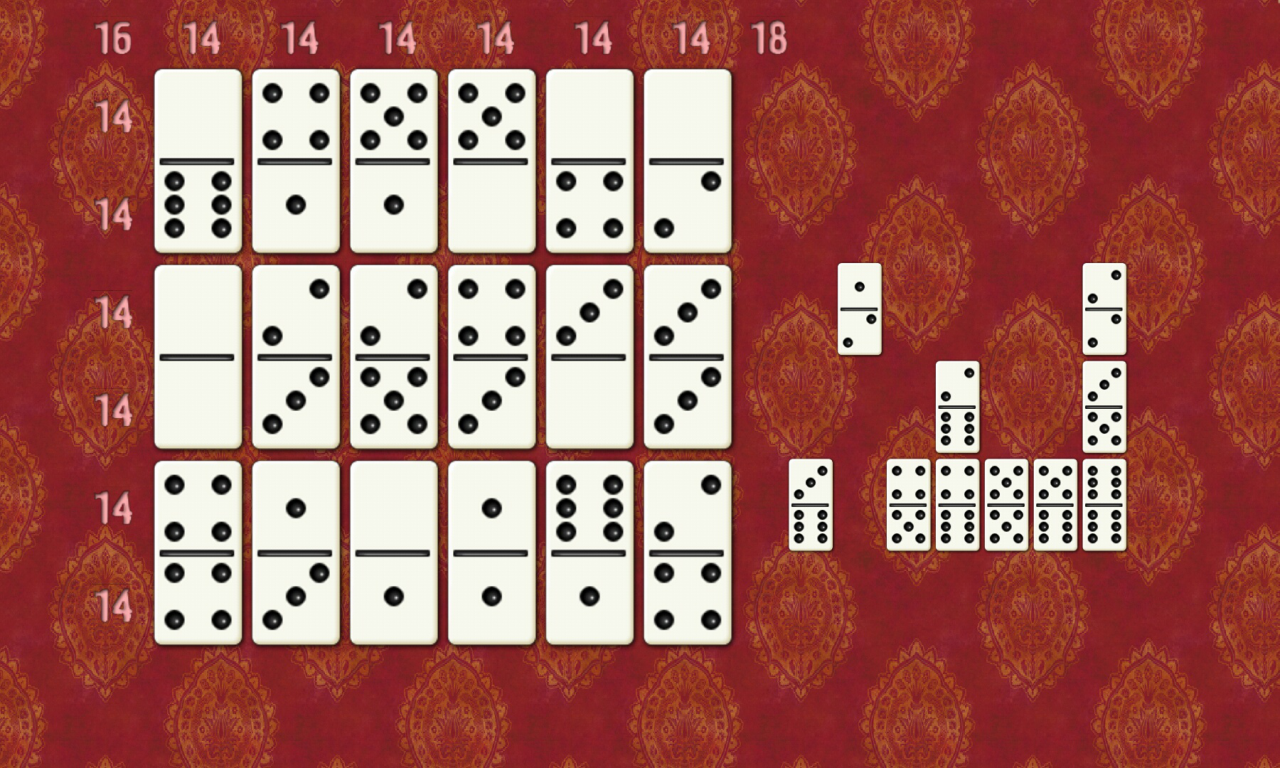
将代码的最前面的“int num[6][6] ;需要硬编码进来”改成
int num[6][6] = {0, 4, 5, 5, 0, 0,6, 1, 1, 0, 4, 2,0, 2, 2, 4, 3, 3,0, 3, 5, 3, 0, 3,4, 1, 0, 1, 6, 2,4, 3, 1, 1, 1, 4 };
运行得到
0 4 5 0 0 5
6 1 0 2 4 1
4 1 1 2 6 0
4 3 1 4 1 1
0 2 4 3 3 2
0 3 3 3 0 5
所以对应的解决方案是

53多米诺骨牌(4)
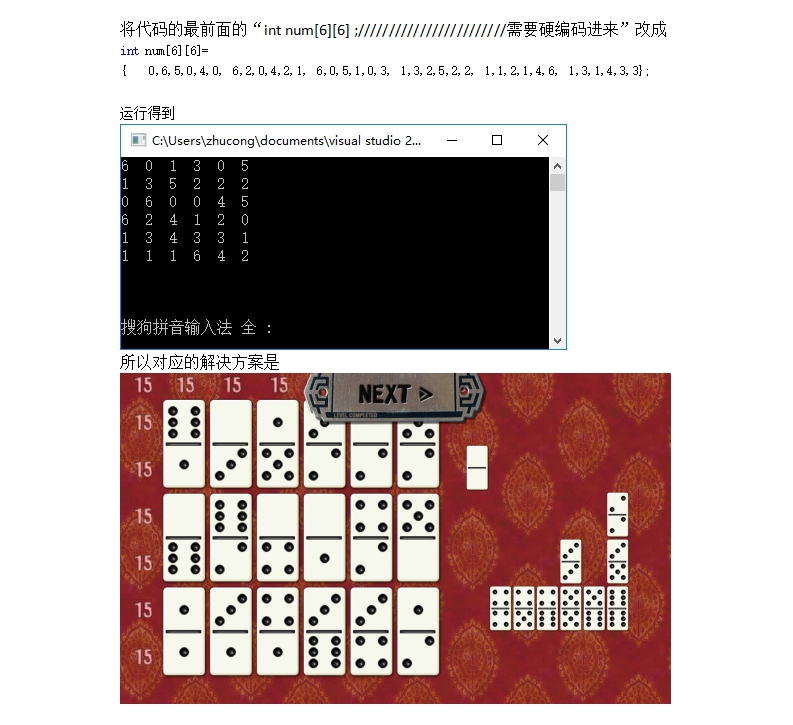
68多米诺骨牌(5)

81多米诺骨牌(6)

94(7)
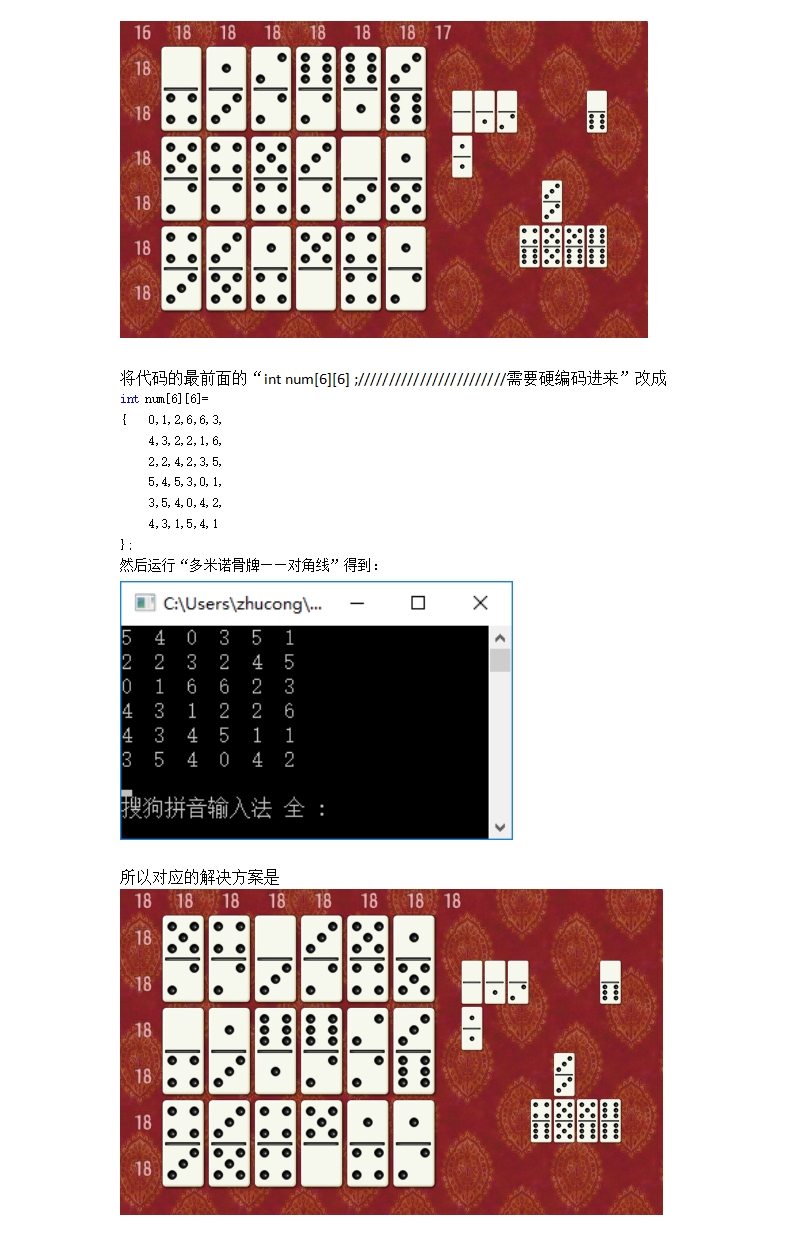
106 多米诺骨牌(12)119(8)130(9)142(10)150(11)
在23多米诺骨牌(2)、38多米诺骨牌(3)53(4)68(5)81(6)94(7)中,分别解决了行和、列和、对角线和均为13、14、15、16、17、18的问题。
根据对称性,如果把6*6的矩阵中的每个数都从k换成6-k,那么原先行和、列和、对角线和均为n的局面就恰好换成了行和、列和、对角线和均为36-n的局面。
也就是说,根据13、14、15、16、17的答案,可以直接得到23、22、21、20、19的答案
106 多米诺骨牌(12)
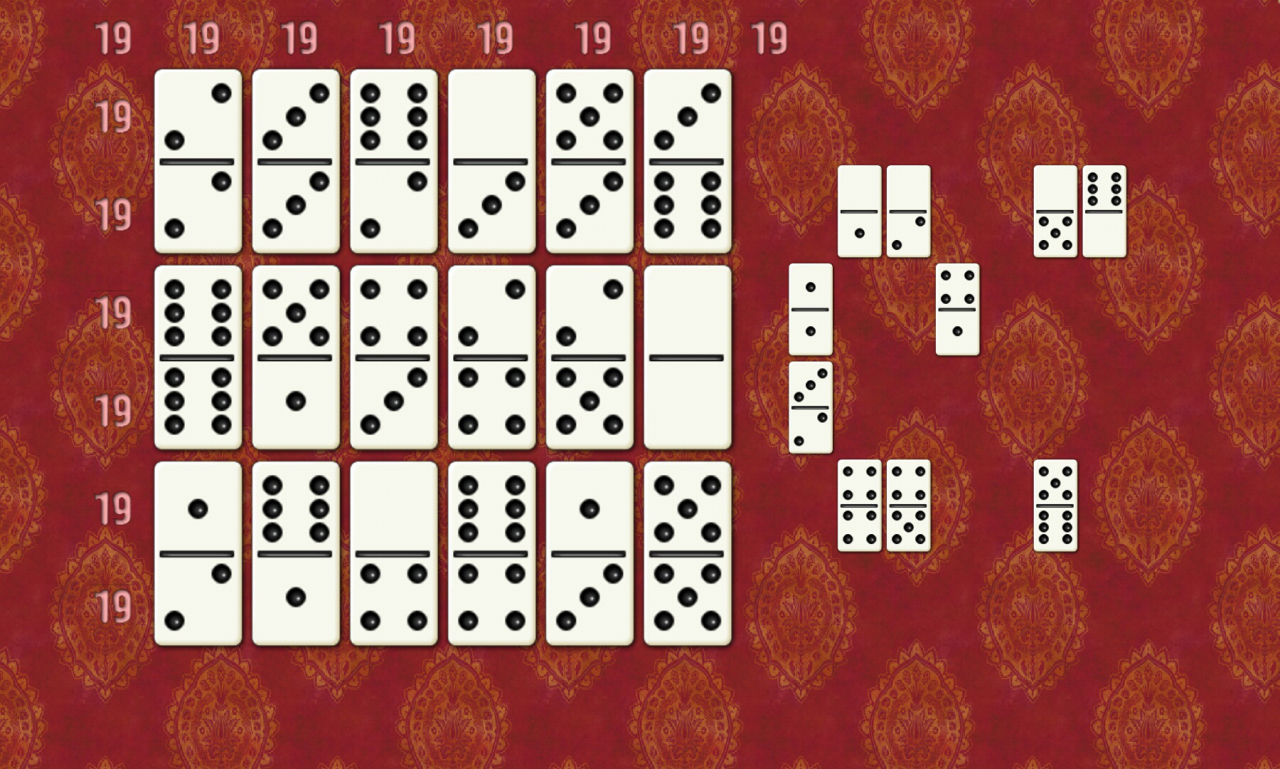
119(8)
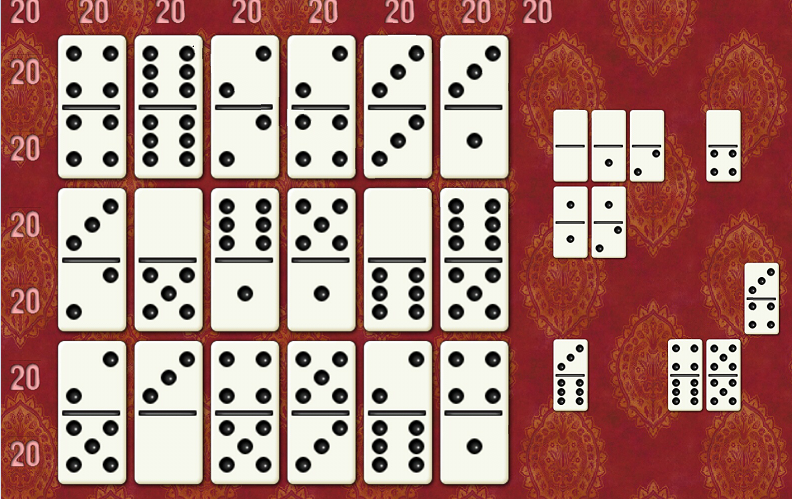
130(9)

142(10)

150(11)

Domino(逻辑数字)
重排骨牌,使得相邻的2个骨牌数字相同。
简单


普通


困难

文章来源: blog.csdn.net,作者:csuzhucong,版权归原作者所有,如需转载,请联系作者。
原文链接:blog.csdn.net/nameofcsdn/article/details/126672852
- 点赞
- 收藏
- 关注作者



评论(0)