@TOC

简介

Hello！
非常感谢您阅读海轰的文章，倘若文中有错误的地方，欢迎您指出～
 
ଘ(੭ˊᵕˋ)੭
昵称：海轰
标签：程序猿｜C++选手｜学生
简介：因C语言结识编程，随后转入计算机专业，获得过国家奖学金，有幸在竞赛中拿过一些国奖、省奖…已保研
学习经验：扎实基础 + 多做笔记 + 多敲代码 + 多思考 + 学好英语！
 
唯有努力💪
 
本文仅记录自己感兴趣的内容

比赛结果

很久没有参加比赛了， 稍微有点紧张

第一题犹豫了一会

第二题直接就暴力模拟了

第三题思路想到了，DFS，不过写的时候没有注意优化，其实可以再简化一下的…

第四题，不会…

第五题，超时了，意料之中，因为没有想到正确的解法，这里是使用回溯模拟所有的情况，然后再使用滑动窗口（应该就是回溯那里有问题 直觉告诉应该有简便的方法）

总的结果还是挺满意的，不过也发现了很多不足的地方

再接再厉！好好学习！

1. 气温变化趋势

力扣城计划在两地设立「力扣嘉年华」的分会场，气象小组正在分析两地区的气温变化趋势，对于第 i ~ (i+1) 天的气温变化趋势，将根据以下规则判断：

• 若第 i+1 天的气温 高于 第 i 天，为 上升 趋势
• 若第 i+1 天的气温 等于 第 i 天，为 平稳 趋势
• 若第 i+1 天的气温 低于 第 i 天，为 下降 趋势

已知 temperatureA[i] 和 temperatureB[i] 分别表示第 i 天两地区的气温

组委会希望找到一段天数尽可能多，且两地气温变化趋势相同的时间举办嘉年华活动。请分析并返回两地气温变化趋势相同的最大连续天数。

即最大的 n，使得第 i~i+n 天之间，两地气温变化趋势相同

思路：

• 直接模拟，统计趋势相同的数量
• 最后return 最大值即可

代码：

class Solution {
public:
    int temperatureTrend(vector<int>& temperatureA, vector<int>& temperatureB) {
        int cnt = 0;
        int ans = 0;
        int n = temperatureA.size();
        for(int i = 1; i < n; ++i) {
            if((temperatureA[i] - temperatureA[i-1]) > 0 && (temperatureB[i] - temperatureB[i-1]) > 0) {
                ++cnt;
            } else if((temperatureA[i] - temperatureA[i-1]) < 0 && (temperatureB[i] - temperatureB[i-1]) < 0) {
                ++cnt;
            } else if((temperatureA[i] - temperatureA[i-1]) == 0 && (temperatureB[i] - temperatureB[i-1]) == 0) {
                ++cnt;
            } else {
                ans = max(ans, cnt);
                cnt = 0;
            }
        }
        ans = max(ans, cnt);
        return ans;
    }
};

2. 交通枢纽

为了缓解「力扣嘉年华」期间的人流压力，组委会在活动期间开设了一些交通专线。path[i] = [a, b] 表示有一条从地点 a通往地点 b 的 单向 交通专线。

若存在一个地点，满足以下要求，我们则称之为 交通枢纽：

• 所有地点（除自身外）均有一条 单向 专线 直接 通往该地点；
• 该地点不存在任何 通往其他地点 的单向专线。

请返回交通专线的 交通枢纽。若不存在，则返回 -1。

注意：

• 对于任意一个地点，至少被一条专线连通。

示例 1：

思路：

• 先使用unordered_set 记录所有出现的节点
• 同时使用unordered_map记录节点，及其指向这个节点的节点集
• 然后遍历unordered_map，查看对应节点集的数量，如果等于总数-1
• 那么就再查看此时节点是否出现在path中节点对的第一个元素中

本质还是暴力模拟，哈哈哈（没有想到其他解法）

代码：

class Solution {
public:
    int transportationHub(vector<vector<int>>& path) {
        unordered_set<int> us;
        unordered_map<int, vector<int>> um;
        int n = path.size();
        for(int i = 0; i < n; ++i) {
            us.insert(path[i][0]);
            us.insert(path[i][1]);
            um[path[i][1]].push_back(path[i][0]);
        }
        for(auto it : um) {
            if(it.second.size() == us.size() - 1) {
                int node = it.first;
                bool flag = true;
                for(int  i = 0; i < n; ++i) {
                    if(path[i][0] == node) {
                        flag = false;
                        break;
                    }
                }
                if(flag == true) {
                    return node;
                }
            }
        }
        return -1;
    }
};

3. 弹珠游戏

欢迎各位来到「力扣嘉年华」，接下来将为各位介绍在活动中广受好评的弹珠游戏。

N*M 大小的弹珠盘的初始状态信息记录于一维字符串型数组 plate 中，数组中的每个元素为仅由 “O”、“W”、“E”、"." 组成的字符串。其中：

• “O” 表示弹珠洞（弹珠到达后会落入洞中，并停止前进）；
• “W” 表示逆时针转向器（弹珠经过时方向将逆时针旋转 90 度）；
• “E” 表示顺时针转向器（弹珠经过时方向将顺时针旋转 90 度）；
• “.” 表示空白区域（弹珠可通行）。

游戏规则要求仅能在边缘位置的 空白区域 处（弹珠盘的四角除外）沿 与边缘垂直 的方向打入弹珠，并且打入后的每颗弹珠最多能 前进 num 步。请返回符合上述要求且可以使弹珠最终入洞的所有打入位置。你可以 按任意顺序 返回答案。

注意：

• 若弹珠已到达弹珠盘边缘并且仍沿着出界方向继续前进，则将直接出界。

思路：

• 这道题是常规DFA的一个改版
• 就是需要判断此时弹珠下一步前进的方向（标记方向）
• 同时有了步数的限制以及W、E的一下限制

这里就直接if_else了
哈哈
开始没有理解到题目，后面又漏了一些判断条件…
代码肯定是可以再简化的，没有时间了 ，只能这样了

代码：

class Solution {
public:
    bool dfs(vector<string>& plate, int row, int col, int steps, int num, int flag) {
        if(steps > num) {
            return false;
        }
        int m = plate.size(), n = plate[0].size();
        if(row < 0 || row >= m || col < 0 || col >= n) {
            return false;
        }
        if(plate[row][col] == 'O') {
            return true;
        }
        if(plate[row][col] == 'W') {
            if(flag == 0) {
                return dfs(plate, row + 1, col, steps + 1, num, flag = 3);
            } else if(flag == 1) {
                return dfs(plate, row, col - 1, steps + 1, num, flag = 0);
            }  else if(flag == 2) {
                return dfs(plate, row - 1, col, steps + 1, num, flag = 1);
            } else if(flag == 3) {
                return dfs(plate, row, col + 1, steps + 1, num, flag = 2);
            }
        }
        if(plate[row][col] == 'E') {
            if(flag == 0) {
                return dfs(plate, row - 1, col, steps + 1, num, flag = 1);
            } else if(flag == 1) {
                return dfs(plate, row, col + 1, steps + 1, num, flag = 2);
            }  else if(flag == 2) {
                return dfs(plate, row + 1, col, steps + 1, num, flag = 3);
            } else if(flag == 3) {
                return dfs(plate, row, col - 1, steps + 1, num, flag = 0);
            }
        }
        if(plate[row][col] == '.') {
            if(flag == 0) {
                return dfs(plate, row, col - 1, steps + 1, num, flag = 0);
            } else if(flag == 1) {
                return dfs(plate, row - 1, col, steps + 1, num, flag = 1);
            }  else if(flag == 2) {
                return dfs(plate, row, col + 1, steps + 1, num, flag = 2);
            } else if(flag == 3) {
                return dfs(plate, row + 1, col, steps + 1, num, flag = 3);
            }
        }
        return false;
    }
    vector<vector<int>> ballGame(int num, vector<string>& plate) {
        vector<vector<int>> ans;
        int m = plate.size(), n = plate[0].size();
        for(int j = 1; j < n - 1; ++j) {
            if(plate[0][j] != 'O' && plate[0][j] != 'W' && plate[0][j] != 'E' && dfs(plate, 0, j, 0, num, 3)) {
                ans.push_back({0, j});
            }
        }
        for(int j = 1; j < n - 1; ++j) {
            if(plate[m - 1][j] != 'O' && plate[m - 1][j] != 'W' && plate[m - 1][j] != 'E' && dfs(plate, m - 1, j, 0, num, 1)) {
                ans.push_back({m - 1, j});
            }
        }
        for(int i = 1; i < m - 1; ++i) {
            if(plate[i][0] != 'O'  && plate[i][0] != 'W' && plate[i][0] != 'E' &&  dfs(plate, i, 0, 0, num, 2)) {
                ans.push_back({i, 0});
            }
        }
        for(int i = 1; i < m - 1; ++i) {
            if(plate[i][n-1] != 'O'  && plate[i][n-1] != 'W' && plate[i][n-1] != 'E' &&  dfs(plate, i, n - 1, 0, num, 0)) {
                ans.push_back({i, n - 1});
            }
        }
        return ans;
    }
};

4. 二叉树灯饰

「力扣嘉年华」的中心广场放置了一个巨型的二叉树形状的装饰树。每个节点上均有一盏灯和三个开关。节点值为 0 表示灯处于「关闭」状态，节点值为 1 表示灯处于「开启」状态。每个节点上的三个开关各自功能如下：

• 开关 1：切换当前节点的灯的状态；
• 开关 2：切换 以当前节点为根 的子树中，所有节点上的灯的状态，；
• 开关 3：切换 当前节点及其左右子节点（若存在的话） 上的灯的状态；

给定该装饰的初始状态 root，请返回最少需要操作多少次开关，可以关闭所有节点的灯。

感觉有点像灯泡开关2这道题，但是没有想出来方法，哎

5. 舒适的湿度

力扣嘉年华为了确保更舒适的游览环境条件，在会场的各处设置了湿度调节装置，这些调节装置受控于总控室中的一台控制器。
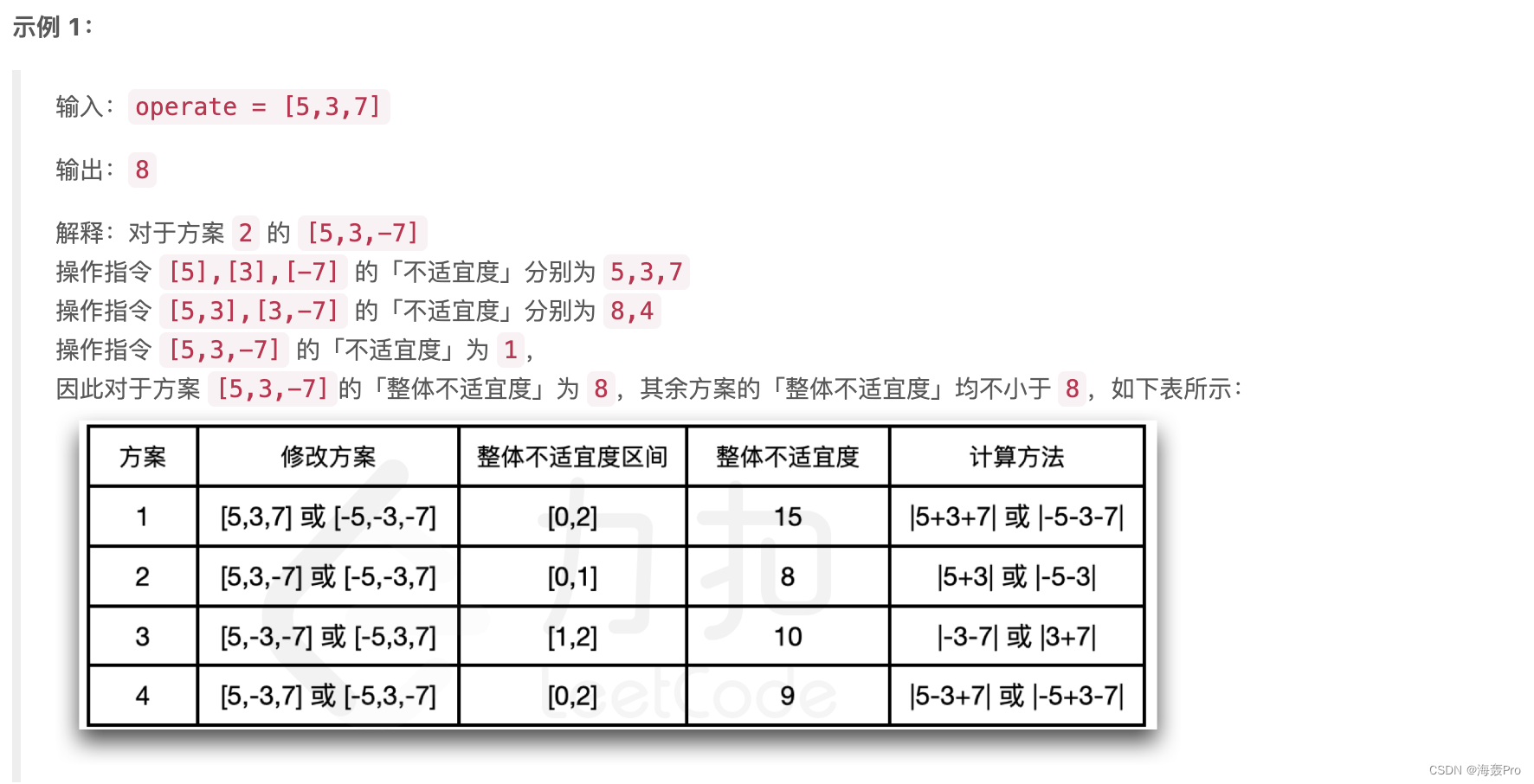
控制器中已经预设了一些调节指令，整数数组operate[i] 表示第 i 条指令增加空气湿度的大小。现在你可以将任意数量的指令修改为降低湿度（变化的数值不变），以确保湿度尽可能的适宜：

• 控制器会选择 一段连续的指令 ，从而进行湿度调节的操作；
• 这段指令最终对湿度影响的绝对值，即为当前操作的「不适宜度」
• 在控制器所有可能的操作中，最大 的「不适宜度」即为「整体不适宜度」

请返回在所有修改指令的方案中，可以得到的 最小 「整体不适宜度」。

思路：

• 先使用回溯找出所有operate的可能（添加负号）
• 然后再使用滑动窗口进行计算

写完就感觉到 肯定会超时了
一般应该是不需要回溯模拟的
奈何没有想到更好的方法
还是得多练习啊

代码：

class Solution {
public:
    vector<vector<int>> arr;
    vector<int> tmp;
    void backTracing(vector<int>& operate, int idx) {
        int n = operate.size();
        if(tmp.size() == n) {
            arr.push_back(tmp);
            return ;
        }
        tmp.push_back(operate[idx]);
        backTracing(operate, idx + 1);
        tmp.pop_back();
        
        tmp.push_back(-1 * operate[idx]);
        backTracing(operate, idx + 1);
        tmp.pop_back();
    }
    int getA(vector<int>& res) {
        int n = res.size();
        int ans = INT_MIN;
        for(int cnt = 0; cnt < n; ++cnt) {
            int max_num = getAbsMax(res, cnt + 1);
            ans = max(ans, max_num);
            // cout << ans << endl;
        }
        return ans;
    }
    int getAbsMax(vector<int>& res, int len) {
        int ans = INT_MIN;
        int w = 0;
        for(int i = 0; i < len; ++i) {
            w += res[i];
        }
        for(int i = 0; i < res.size() - len + 1; ++i) {
            ans = max(ans, abs(w));
            w -= res[i];
            if(i + len < res.size()) {
                w += res[i + len];
            }
        }
        return ans;
    }
    int unSuitability(vector<int>& operate) {
        int n = operate.size();
        backTracing(operate, 0);
        int ans = INT_MAX;
        for(int i = 0; i < arr.size(); ++i) {
            ans = min(ans, getA(arr[i]));
        }
        return ans;
    }
};

结语

文章仅作为个人学习笔记记录，记录从0到1的一个过程

希望对您有一点点帮助，如有错误欢迎小伙伴指正