【C语言】带你走进函数
目录
前言😄
大家好啊,C语言中函数这一块内容是比较重要的,而且内容是比较多的。接下来,我会用这一篇博客来介绍函数的相关知识。函数的实现太过于重要,通过调用不同的函数,可以帮助实现功能,同时,函数的模块化设计,高内聚低耦合,封装性,使代码看起来更加合理整洁。对于我们非常重要。希望本篇博客能够对你有帮助,同时,觉得不错的话,也可以收藏起来哦。
下面,进入我们的主题——函数👇
什么是函数?🍁
函数我们从数学开始就已经在打交道了,那C语言的函数又是什么呢?😖
在计算机科学中,子程序(英语:Subroutine, procedure, function, routine, method, subprogram, callable unit),是一个大型程序中的某部分代码, 由一个或多个语句块组 成。它负责完成某项特定任务,而且相较于其他代 码,具备相对的独立性。
一般会有输入参数并有返回值,提供对过程的封装和细节的隐藏。这些代码通常被集成为软 件库。
了解完函数的基本概念之后,我们在来看看函数类型
C语言函数的分类🍁
1.库函数
2.自定义函数
1.库函数
什么是库函数呢?这不得不说库函数的由来了📄
我们学习C语言编程的时候,总是在一个代码编写完成之后迫不及待的想知道结果,这个时候我们会频繁的使用一个功能:将信息按照一定的格 式打印到屏幕上(printf)。
在编程的过程中我们会频繁的做一些字符串的拷贝工作(strcpy)。
在编程是我们也计算,总是会计算n的k次方这样的运算(pow)。 像上面我们描述的基础功能,它们不是业务性的代码。我们在开发的过程中每个程序员都可能用的到, 为了支持可移植性和提高程序的效率,所以C语言的基础库中提供了一系列类似的库函数,方便程序员 进行软件开发。
对于库函数来说,我们该怎么去学习呢?
首先,我们可以尝试前往官网::www.cplusplus.com
打开以后,就是这样子的,可千万别因为是英文就跑路了!😠
其实在学习编程的过程中遇到英文是比较常见的事情,我们更应该适应英文的环境,当然,如果看不懂的时候可以翻译一下。
先来说一说,C语言常用的库函数都有🆕
IO函数
字符串操作函数
字符操作函数
内存操作函数
时间/日期函数
数学函数
其他库函数
下面,我们基于上述官网简单演示一下如何使用🚑
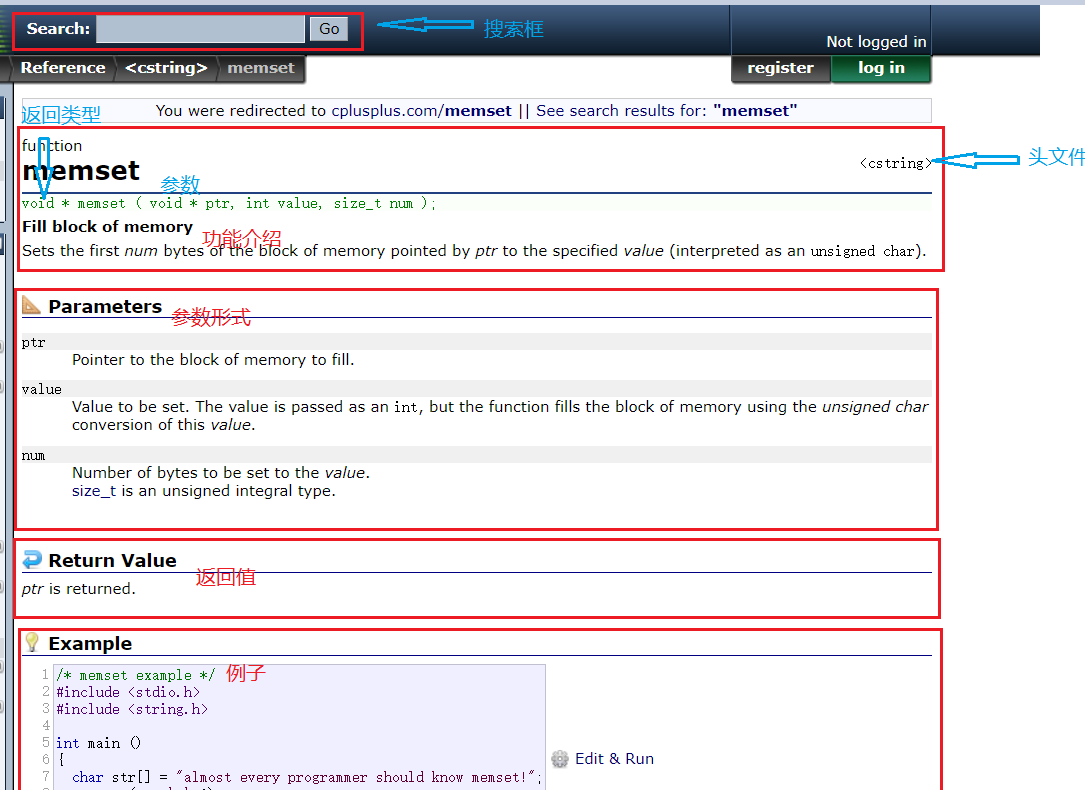
这里以memset函数为介绍:
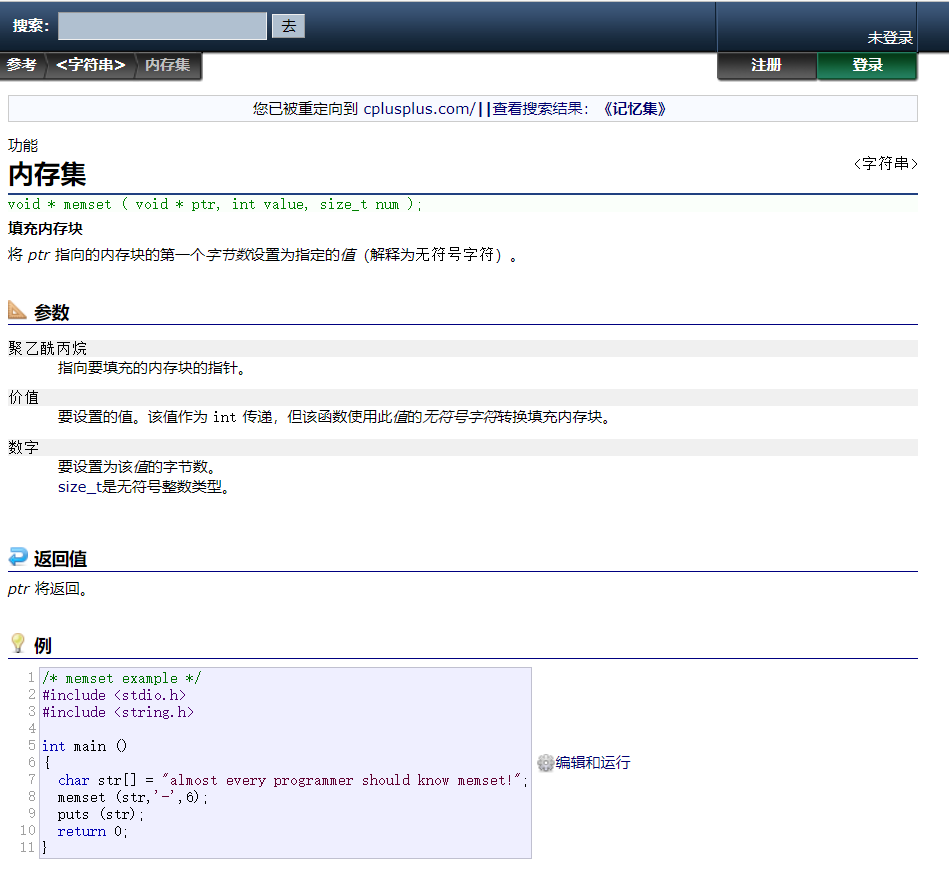
英文实在看不懂的话,那就直接翻译了✅
对于一些库函数,我们可能没怎么用过,这时候就可以查查怎么使用了
注意点: 但是库函数必须知道的一个秘密就是:使用库函数,必须包含 #include 对应的头文件。 这里对照文档来学习上面几个库函数,目的是掌握库函数的使用方法。
2.怎么使用?
你能会在想:需不需要全都记下来?NO❎
我们可以用到插库函数的工具有:MSDN,以及上述官网等等
自定义函数
库函数并不能解决所有的问题,如果库函数能干所有的事情,那还要程序员干什么?
更加重要的是自定义函数。 自定义函数和库函数一样,有函数名,返回值类型和函数参数。 但是不一样的是这些都是我们自己来设计。 函数的基本形式:
ret_type fun_name(para1, * )
{
statement;//语句项
}
ret_type 返回类型
fun_name 函数名
para1 函数参数
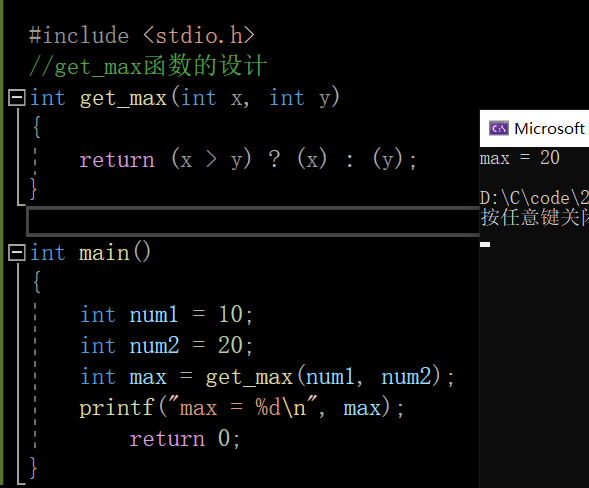
我们可以简单来举个例子理解理解,比如自定义实现找两个数中的较大数(打开vs新建文件)
这里并不存在形参改变不了实参的问题,这里有变量去接收返回值,别搞混了🔥这里给出代码,显示一下形参改变不了实参的情况:
好啦,关于函数的分类就先介绍到这里了
函数的参数🍁
实际参数(实参)
真实传给函数的参数,叫实参。 实参可以是:常量、变量、表达式、函数等。 无论实参是何种类型的量,在进行函数调用时,它们都必须有确定的值,以便把这些值传送给形参。
形式参数(形参)
形式参数是指函数名后括号中的变量,因为形式参数只有在函数被调用的过程中才实例化(分配内 存单 元),所以叫形式参数。形式参数当函数调用完成之后就自动销毁了。因此形式参数只在函数中有 效。
怎么去理解呢?我们以上述例子为说明:
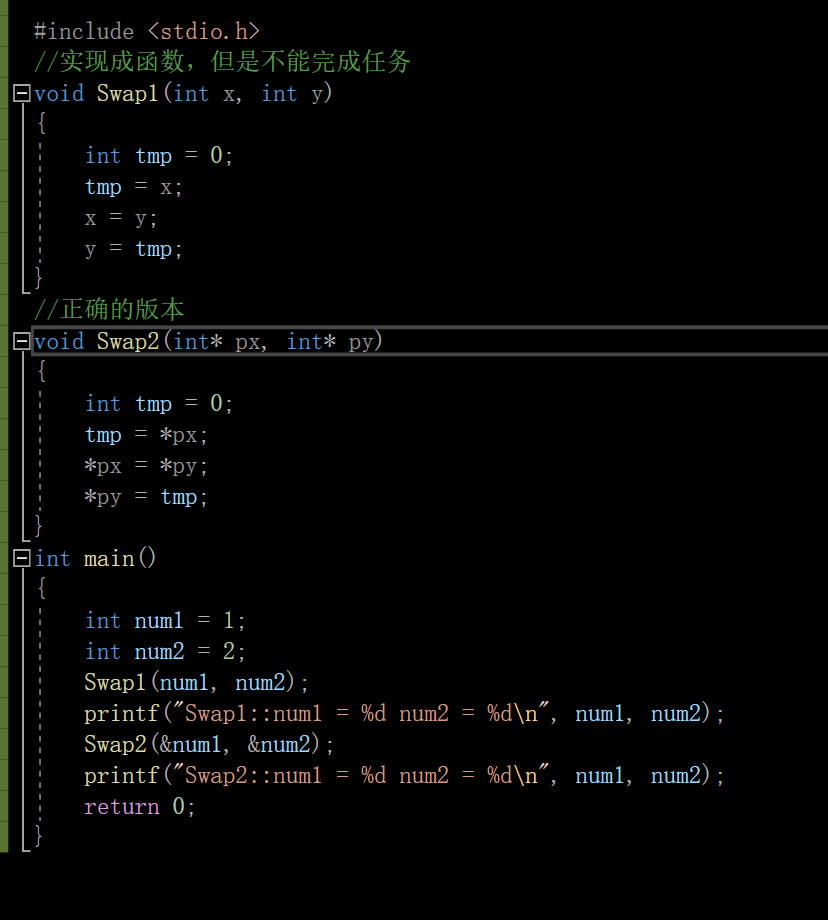
上面 Swap1 和 Swap2 函数中的参数 x,y,px,py 都是形式参数。在main函数中传给 Swap1 的 num1 , num2 和传 给 Swap2 函数的 &num1 , &num2 是实际参数。
函数的调用🍁
函数调用有两种方式:传值调用,传址调用(Swap1就是传值调用,Swap2就是传址调用)
传值调用
函数的形参和实参分别占有不同内存块,对形参的修改不会影响实参。
传址调用
传址调用是把函数外部创建变量的内存地址传递给函数参数的一种调用函数的方式。 这种传参方式可以让函数和函数外边的变量建立起真正的联系,也就是函数内部可以直接操 作函数外部的变量。
基于传值调用和传址调用,我们可以根据不同的实际情况做出不同的设计。
基于此,可以看看我之前写过的博客:
函数的嵌套调用和链式访问🍁
函数的嵌套调用
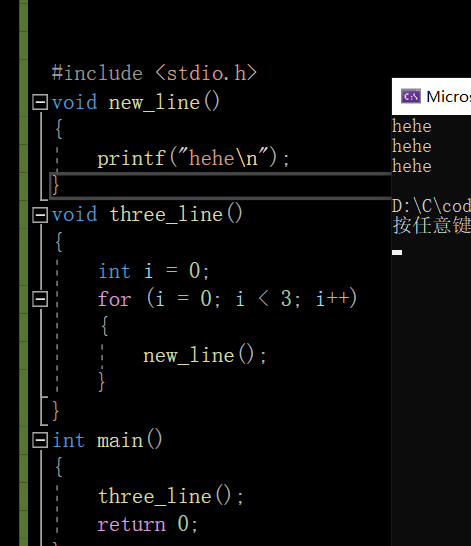
函数与函数直接也是可以建立起联系的🔗可以相互嵌套既可以相互调用。简单举个例子🌰
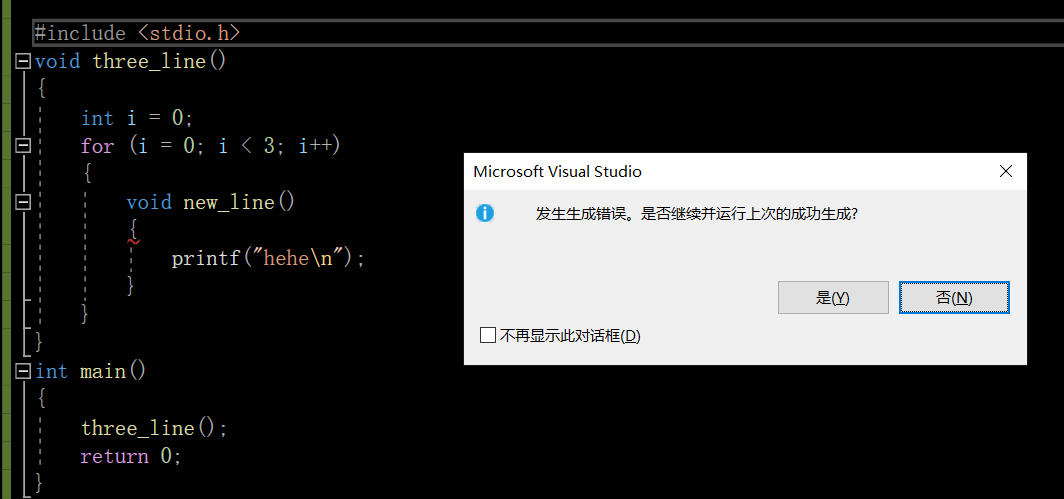
注意:函数虽然可以嵌套调用,但是不能认为可以嵌套定义!!!🇪🇷
改一下上面代码⏬
编译直接出错🚫
函数的链式访问
什么是链式访问呢?把一个函数的返回值作为另外一个函数的参数。📶这其实意味着函数要有返回值!
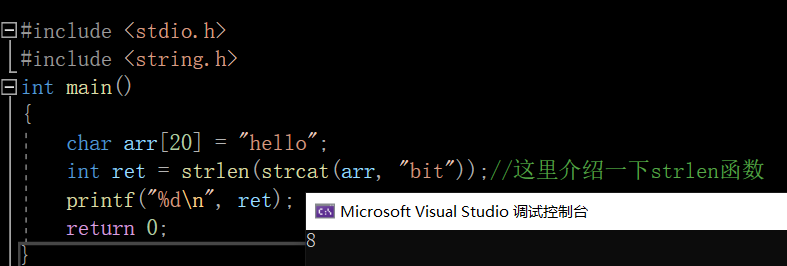
下面我们来举个例子练习一下,加深印象
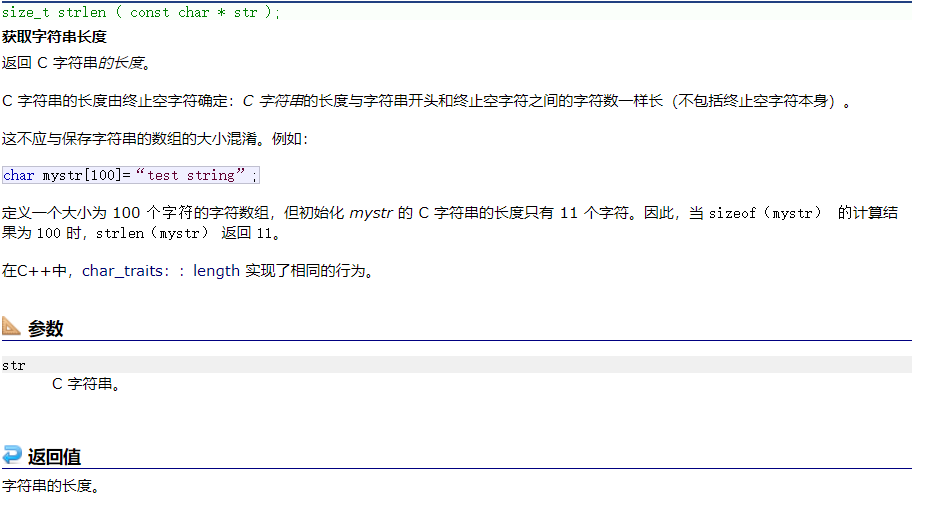
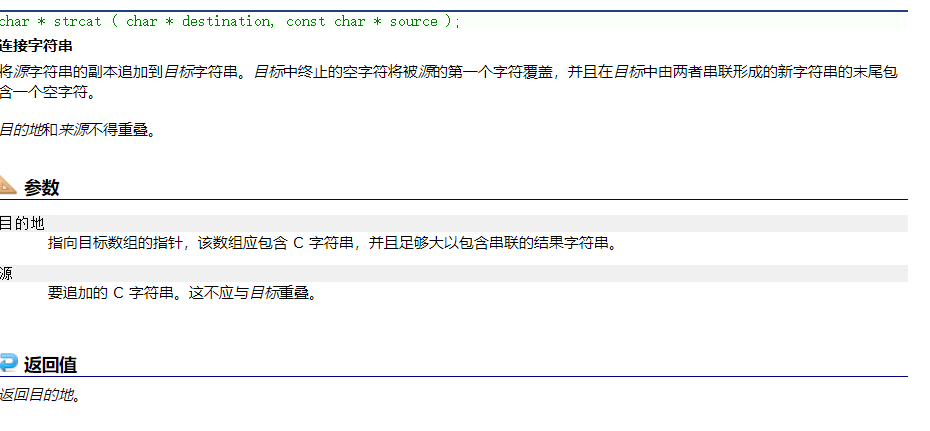
这时候肯定有人要问了,strlen是什么,strcat又是什么???😏
简单介绍一下,strlen返回字符串长度,strcat连接字符串
好了,基于对这两个函数的理解,我们不难知道为什么会输出8了。
下面,在来看看我们自认为很熟悉的printf函数的链式访问会发生什么
你真的对printf函数很熟悉吗?printf其实是有返回值的:
好了,基于上面的了解,我们来看看代码:
首先先打印出43,然后43会返回2,2会返回1,所以会输出4321!
你学废了吗?
函数的声明和定义🍁
函数的声明:函数声明只是对编译系统的一个说明:.函数声明是对定义的函数的返回值的类型说明,以通知系统在本函数中所调用的函数是什么类型。
函数的定义是指函数的具体实现,交待函数的功能实现。函数的定义其实就是自定义函数,自己怎么去设计,有没有返回值、参数,参数的类型是什么,该怎么去实现等等问题
其实我比较不喜欢的就是学校的很多教材都喜欢把函数的声明写在前面,但是其实我们放在主main()函数的时候就不要去声明了。
然后函数的声明真正的用法是在于模块化设计,体现程序的高内聚低耦合
函数递归🍁
什么是递归?
程序调用自身的编程技巧称为递归( recursion)。 递归做为一种算法在程序设计语言中广泛应用。 一个过程或函数在其定义或说明中有直接或间接 调用自身的 一种方法,它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解, 递归策略 只需少量的程序就可描述出解题过程所需要的多次重复计算,大大地减少了程序的代码量。
递归的主要思想方式在于:大事化小!
许多题目可能用递归方法做起来反而更加简单,比如后续学数据结构二叉树中的遍历时,采用递归的方法往往更加简单,但是可能又考虑到效率问题,一些题目存在于对时间复杂度有要求等,这时候我们往往需要学会把递归的实现方式转换为非递归的实现方式。
递归的必要条件
存在限制条件,当满足这个限制条件的时候,递归便不再继续。
每次递归调用之后越来越接近这个限制条件
递归必须存在条件,不然的话只能层层递归不返回
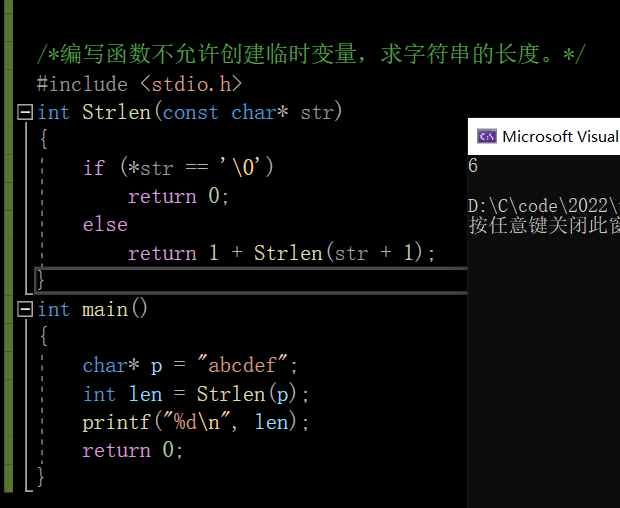
一些递归题目在我上面提到的博客也有介绍到,这里以一道题来作为例子把:
主要思想:当字符串为空的时候自然返回0,然后调用自己,完后走一位,走之前先加1直到结束
然后关于一些其他的递归题目我就在这里不展开说了,斐波那契数列我在那一篇博客也有介绍到
关于递归我主要想说的是一个非常典型的递归问题:
汉诺塔问题
汉诺塔问题
汉诺塔问题是什么?
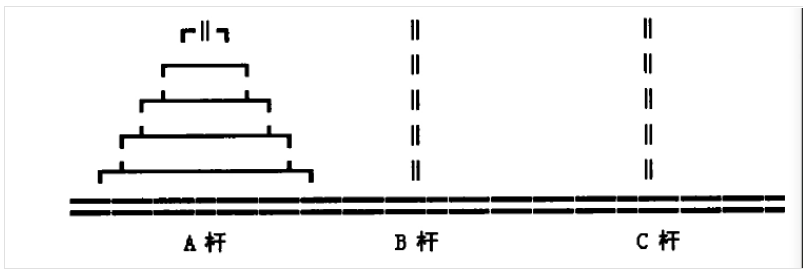
相传在古印度圣庙中,有一种被称为汉诺塔(Hanoi)的游戏。该游戏是在一块铜板装置上,有三根杆(编号A、B、C),在A杆自下而上、由大到小按顺序放置64个金盘(如图1)。游戏的目标:把A杆上的金盘全部移到C杆上,并仍保持原有顺序叠好。操作规则:每次只能移动一个盘子,并且在移动过程中三根杆上都始终保持大盘在下,小盘在上,操作过程中盘子可以置于A、B、C任一杆上。
怎么解决,具体思路:
(1)以C盘为中介,从A杆将1至n-1号盘移至B杆;
(2)将A杆中剩下的第n号盘移至C杆;
(3)以A杆为中介;从B杆将1至n-1号盘移至C杆
但是只有第二步可直接完成,而第一、三步又成为移动的新问题。以上操作的实质是把移动n个盘子的问题转化为移动n-1个盘,那一、三步如何解决?事实上,上述方法设盘子数为n, n可为任意数,该法同样适用于移动n-1个盘。因此,依据上法,可解决n -1个盘子从A杆移到B杆(第一步)或从B杆移到C杆(第三步)问题。现在,问题由移动n个盘子的操作转化为移动n-2个盘子的操作。依据该原理,层层递推,即可将原问题转化为解决移动n -2、n -3… … 3、2,直到移动1个盘的操作,而移动一个盘的操作是可以直接完成的。至此,我们的任务算作是真正完成了。而这种由繁化简,用简单的问题和已知的操作运算来解决复杂问题的方法,就是递归法。
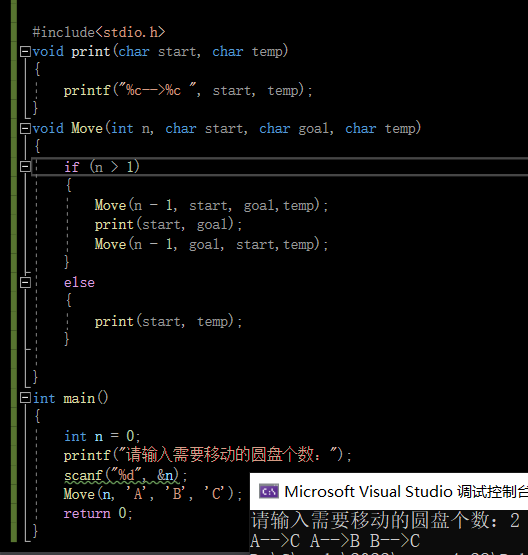
代码实现:
结束语😄
好啦,本次博客有关函数的介绍就到这里结束了,感谢你的支持哦🌹
- 点赞
- 收藏
- 关注作者










评论(0)