python3 高斯函数
【摘要】
1.涉及公式
1.1 高斯分布公式
概率密度函数
1.2 二项分布公式
换句话说,一枚公平的硬币有正面结果的概率(正面)p = 0.5。如果你掷硬币 20 次,平均值为 20 * 0.5 ...
1.涉及公式
1.1 高斯分布公式
概率密度函数
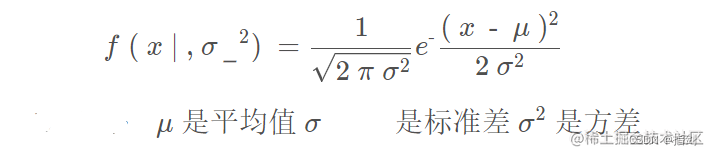
1.2 二项分布公式
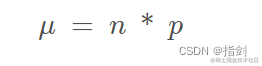
换句话说,一枚公平的硬币有正面结果的概率(正面)p = 0.5。如果你掷硬币 20 次,平均值为 20 * 0.5 = 10;你会期望得到10个正面
1.3 方差
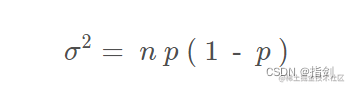
继续以硬币为例,n 是投掷硬币的次数,p 是正面朝上的概率
1.4 标准差
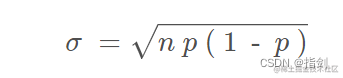
换句话说,标准差是方差的平方根。
1.5 概率密度函数
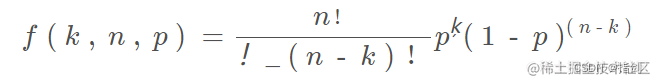
2.编写高斯类
import math
import matplotlib.pyplot as plt
class Gaussian():
""" 高斯分布类,用于计算和可视化高斯分布.
Attributes:
均值(float),表示分布的均值。stdev(float)表示分布数据的标准偏差。_ list(float列表):从数据文件中提取的浮点列表
"""
def __init__(self, mu = 0, sigma = 1):
self.mean = mu
self.stdev = sigma
self.data = []
def calculate_mean(self):
"""函数计算数据集的平均值.
Args:
None
Returns:
float: mean of the data set
"""
avg = 1.0 * sum(self.data) / len(self.data)
self.mean = avg
return self.mean
def calculate_stdev(self, sample=True):
"""函数计算数据集的标准偏差.
Args:
sample (bool): 数据是代表样本还是总体
Returns:
float: 数据集的标准偏差
"""
if sample:
n = len(self.data) - 1
else:
n = len(self.data)
mean = self.mean
sigma = 0
for d in self.data:
sigma += (d - mean) ** 2
sigma = math.sqrt(sigma / n)
self.stdev = sigma
return self.stdev
def read_data_file(self, file_name, sample=True):
"""函数从txt文件读入数据。txt文件应该具有每行一个数字(浮动)。这些数字存储在数据属性中。读取文件后,计算平均值和标准偏差
Args:
file_name (string): name of a file to read from
Returns:
None
"""
with open(file_name) as file:
data_list = []
line = file.readline()
while line:
data_list.append(int(line))
line = file.readline()
file.close()
self.data = data_list
self.mean = self.calculate_mean()
self.stdev = self.calculate_stdev(sample)
def plot_histogram(self):
"""函数使用matplotlib pyplot库输出实例变量数据的直方图.
Args:
None
Returns:
None
"""
plt.hist(self.data)
plt.title('Histogram of Data')
plt.xlabel('data')
plt.ylabel('count')
def pdf(self, x):
"""高斯分布的概率密度函数计算器.
Args:
x (float): 计算概率密度函数的点
Returns:
float: 输出的概率密度函数
"""
return (1.0 / (self.stdev * math.sqrt(2*math.pi))) * math.exp(-0.5*((x - self.mean) / self.stdev) ** 2)
def plot_histogram_pdf(self, n_spaces = 50):
"""函数绘制数据的归一化直方图,并沿相同范围绘制概率密度函数
Args:
n_spaces (int): number of data points
Returns:
list: x values for the pdf plot
list: y values for the pdf plot
"""
mu = self.mean
sigma = self.stdev
min_range = min(self.data)
max_range = max(self.data)
# 计算x值之间的间隔
interval = 1.0 * (max_range - min_range) / n_spaces
x = []
y = []
# calculate the x values to visualize
for i in range(n_spaces):
tmp = min_range + interval*i
x.append(tmp)
y.append(self.pdf(tmp))
# make the plots
fig, axes = plt.subplots(2,sharex=True)
fig.subplots_adjust(hspace=.5)
axes[0].hist(self.data, density=True)
axes[0].set_title('Normed Histogram of Data')
axes[0].set_ylabel('Density')
axes[1].plot(x, y)
axes[1].set_title('Normal Distribution for \n Sample Mean and Sample Standard Deviation')
axes[0].set_ylabel('Density')
plt.show()
return x, y
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
- 166
- 167
3.测试高斯类
import unittest
class TestGaussianClass(unittest.TestCase):
def setUp(self):
self.gaussian = Gaussian(25, 2)
def test_initialization(self):
self.assertEqual(self.gaussian.mean, 25, 'incorrect mean')
self.assertEqual(self.gaussian.stdev, 2, 'incorrect standard deviation')
def test_pdf(self):
self.assertEqual(round(self.gaussian.pdf(25), 5), 0.19947,\
'pdf function does not give expected result')
def test_meancalculation(self):
self.gaussian.read_data_file('numbers.txt', True)
self.assertEqual(self.gaussian.calculate_mean(),\
sum(self.gaussian.data) / float(len(self.gaussian.data)), 'calculated mean not as expected')
def test_stdevcalculation(self):
self.gaussian.read_data_file('numbers.txt', True)
self.assertEqual(round(self.gaussian.stdev, 2), 92.87, 'sample standard deviation incorrect')
self.gaussian.read_data_file('numbers.txt', False)
self.assertEqual(round(self.gaussian.stdev, 2), 88.55, 'population standard deviation incorrect')
tests = TestGaussianClass()
tests_loaded = unittest.TestLoader().loadTestsFromModule(tests)
unittest.TextTestRunner().run(tests_loaded)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
文章来源: blog.csdn.net,作者:指剑,版权归原作者所有,如需转载,请联系作者。
原文链接:blog.csdn.net/fly1574/article/details/126438008
【版权声明】本文为华为云社区用户转载文章,如果您发现本社区中有涉嫌抄袭的内容,欢迎发送邮件进行举报,并提供相关证据,一经查实,本社区将立刻删除涉嫌侵权内容,举报邮箱:
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者



评论(0)