递归巧解古印度汉诺塔问题
汉诺塔(又称河内塔)问题是源于印度一个古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。
汉罗塔问题背景介绍
汉诺塔问题,是心理学实验研究常用的任务之一。该问题的主要材料包括三根高度相同的柱子和一些大小及颜色不同的圆盘,三根柱子分别为起始柱A、辅助柱B及目标柱C。
相传在古印度圣庙中,有一种被称为汉诺塔(Hanoi)的游戏。该游戏是在一块铜板装置上,有三根杆(编号A、B、C),在A杆自下而上、由大到小按顺序放置64个金盘。游戏的目标:把A杆上的金盘全部移到C杆上,并仍保持原有顺序叠好。操作规则:每次只能移动一个盘子,并且在移动过程中三根杆上都始终保持大盘在下,小盘在上,操作过程中盘子可以置于A、B、C任一杆上。(摘自百度百科)
从上面的资料我们可以提取出一个问题:
Hanoi(汉诺)塔问题。古代有一个梵塔,塔内有3个座A,B,C。开始时A座上有64个盘子,盘子大小不等,大的在下,小的在上。有一个先知想把这64个盘子从A座移到C座,但规定每次只允许移动一个盘,且在移动过程中在3个座上都始终保持大盘在下,小盘在上。在移动过程中可以利用B座。你能帮这位先知实现他的想法吗?要求编程序输出移动盘子的步骤。
解题思路:
这位先知会这样想: 假如有另外一位先知能有办法将上面63个盘子从A座移到B座。那么,问题就解决了。此时先知只须这样做:
① 联系他的好朋友第2个先知将63个盘子从A座移到B座;
② 自己将1个盘子(最底下的、最大的盘子)从A座移到C座;
③ 再让第2个先知将63个盘子从B座移到C座。
第2个先知又想: 如果有人能将62个盘子从一个座移到另一座,我就能将63个盘子从A座移到B座,他是这样做的:
① 联系他的好朋友第3个先知将62个盘子从A座移到C座;
② 自己将1个盘子从A座移到B座;
③ 再让第3个先知将62个盘子从C座移到B座。
……
以此类推

为了便于理解,我们将盘子数量降低到3个,所以首先分析将A座上3个盘子移到C座上的过程:
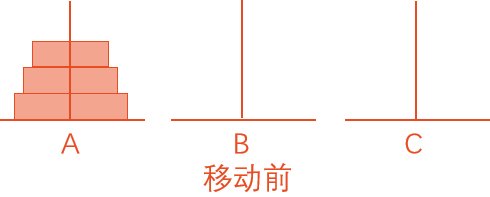
① 将A座上2个盘子移到B座上(借助C座)。

② 将A座上1个盘子移到C座上。

③ 将B座上2个盘子移到C座上(借助A座)。

其中第②步可以直接实现。第①步又可用递归方法分解为:
- 将A座上1个盘子从A座移到C座;
- 将A座上1个盘子从A座移到B座;
- 将C座上1个盘子从C座移到B座。
第③步可以分解为:
- 将B座上1个盘子从B座移到A座上;
- 将B座上1个盘子从B座移到C座上;
- 将A座上1个盘子从A座移到C座上。
将以上综合起来,可得到移动3个盘子的步骤为:
A→C,A→B,C→B,A→C,B→A,B→C,A→C。
共经历7步。由此可推出: 移动n个盘子要经历(2^n^-1)步。
由上面的分析可知: 将n个盘子从A座移到C座可以分解为以下3个步骤:
① 将A座上n-1个盘借助C座先移到B座上;
② 把A座上剩下的一个盘移到C座上;
③ 将n-1个盘从B座借助于A座移到C座上。
可以把上面3个步骤分成两类操作:
① 将n-1个盘从一个座移到另一个座上(n>1)。这就是先知让他的朋友第2个先知做的工作,它是一个递归的过程,即先知将任务层层下放,直到第64个先知为止。——hanoi函数
② 将1个盘子从一个座上移到另一座上。这是先知自己做的工作。——move函数
#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
/*Hanoi(汉诺)塔问题。古代有一个梵塔,塔内有3个座A,B,C。
开始时A座上有64个盘子,盘子大小不等,大的在下,小的在上。
有一个先知想把这64个盘子从A座移到C座,但规定每次只允许移动一个盘,
且在移动过程中在3个座上都始终保持大盘在下,小盘在上。
在移动过程中可以利用B座。你能帮这位先知实现他的想法吗?
要求编程序输出移动盘子的步骤。*/
void hanoi(int n, char a, char b, char c);////定义hanoi函数
//将n个盘从a座借助b座,移到c座
void move(char x, char y);
int main()
{
int lay = 0;
scanf("%d", &lay);
hanoi(lay, 'A', 'B', 'C');//输入盘子个数
//最终输出移动方案
return 0;
}
void move(char x, char y)
{
printf("%c->%c\n", x, y);
}
void hanoi(int n, char a, char b, char c)
{
if (n == 1)
move(a, c);
else
{
hanoi(n - 1, a, c, b);//借c将a移动至b
move(a, c);
hanoi(n - 1, b, a, c);//借a将b移动至c
}
}
根据这个代码让我们来运行一下我们举过移动三个圆盘的例子。

一共7步,与我们举例得出的结果一致。
- 点赞
- 收藏
- 关注作者


评论(0)