虚数是什么
例题:
上海市竞赛题,解方程x³-1=0,求x所有的解。
答:
1、立方差公式拆开可得:
(x-1)(+x+1)=0
题解1:(x-1)=0有x=1
2、由于让求所有解,故而要求(+x+1)=0也有解,需要使用求根公式可得:
题解2:虚数解
以上示例中可以看到,我们平时解题的时候只注意到了实数解,很多时候还会有虚数解,所以在做题的时候要注意题目的要求,这里是要x所有的解,就包含虚数;如果说求x所有的实数解,答个1就行了。
目录
虚数是什么
在数学中,虚数就是形如a+b*i的数,其中a,b是实数,且b≠0,i² = - 1。虚数这个名词是17世纪著名数学家笛卡尔创立,因为当时的观念认为这是真实不存在的数字。后来发现虚数a+b*i的实部a可对应平面上的横轴,虚部b与对应平面上的纵轴,这样虚数a+b*i可与平面内的点(a,b)对应。
可以将虚数bi添加到实数a以形成形式a + bi的复数,其中实数a和b分别被称为复数的实部和虚部。一些作者使用术语纯虚数来表示所谓的虚数,虚数表示具有非零虚部的任何复数。
定义
在数学里,将偶指数幂是负数的数定义为纯虚数。所有的虚数都是复数。定义为i²=-1。但是虚数是没有算术根这一说的,所以±√(-1)=±i。对于z=a+bi,也可以表示为e的iA次方的形式,其中e是常数,i为虚数单位,A为虚数的幅角,即可表示为z=cosA+isinA。实数和虚数组成的一对数在复数范围内看成一个数,起名为复数。虚数没有正负可言。不是实数的复数,即使是纯虚数,也不能比较大小。
符号
1777年瑞士数学家欧拉(Euler,或译为欧勒)开始使用符号i表示虚数的单位。而后人将虚数和实数有机地结合起来,写成a+bi形式 (a、b为实数,a等于0时叫纯虚数,ab都不等于0时叫复数,b等于0时就是实数)。
而在工程运算中,为了不与其他符号(如电流的符号)相混淆,有时也用j或k等字母来表示虚数的单位。
通常,我们用符号C来表示复数集,用符号R来表示实数集。
实际意义
我们可以在平面直角坐标系中画出虚数系统。如果利用横轴表示全体实数,那么纵轴即可表示虚数。整个平面上每一点对应着一个复数,称为复平面。横轴和纵轴也改称为实轴和虚轴。在此时,一点P坐标为P (a,bi),将坐标乘上i即点绕圆心逆时针旋转90度。
不能满足于上述图像解释的同学或学者可参考以下题目和说明:
若存在一个数,它的倒数等于它的相反数(或者它的倒数的相反数为其自身),这个数是什么形式?
根据这一要求,可以给出如下方程:
-x = (1/x)
不难得知,这个方程的解x=±i (虚数单位)
由此,若有t'=ti,我们将i理解为从t的单位到t'的单位之间的转换单位,则t'=ti将被理解为
-t' = 1/t
即
t' = - 1/t
这一表达式在几何空间上的意义不大,但若配合狭义相对论,在时间上理解,则可以解释若相对运动速度可以大于光速c,相对时间间隔产生的虚数值,实质上是其实数值的负倒数。也就是所谓回到过去的时间间隔数值可以由此计算出来。
虚数成为微晶片和数字压缩算法设计中的核心工具,虚数是引发电子学革命的量子力学的理论基础。
虚数是用来表示事物中无法构成抽象概念的因素的抽象概念。
一切事物的值都可表示为:a+bi,而不是单有实数。
i的性质
i 的高次方会不断作以下的循环:
i^1 = i,
i^2= - 1,
i^3 = - i,
i^4 = 1,
i^5 = i,
i^6 = - 1.
...
i^n具有周期性,且最小正周期是4.
∴ i^(4n)=1,
i^(4n+1)=i,
i^(4n+2)=-1,
i^(4n+3)=-i.
由于虚数特殊的运算规则,出现了符号i
当ω=-1/2+(√3)/2i或ω=-1/2-(√3)/2i时:
ω2 + ω + 1 = 0
ω3 = 1
表达式
a=a+i
含义为与一切事物皆无联系的概念,无论a任何变化,i都不会变。
- 点赞
- 收藏
- 关注作者

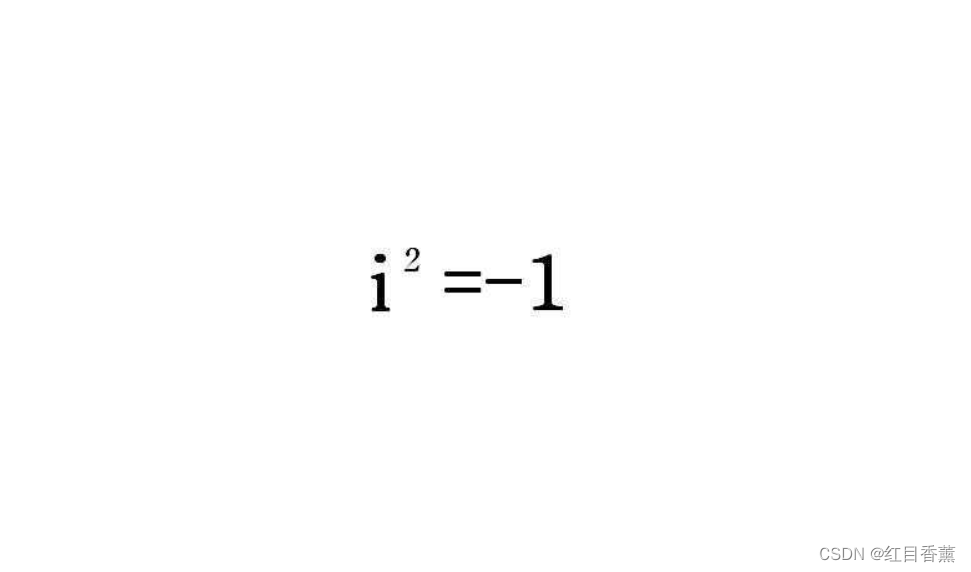


评论(0)