【算法｜习题总结】算法分析与计算复杂性在线测试Ⅰ
【摘要】 @TOC 前言Hello！非常感谢您阅读海轰的文章，倘若文中有错误的地方，欢迎您指出～ 自我介绍 ଘ(੭ˊᵕˋ)੭昵称：海轰标签：程序猿｜C++选手｜学生简介：因C语言结识编程，随后转入计算机专业，获得过国家奖学金，有幸在竞赛中拿过一些国奖、省奖…已保研。学习经验：扎实基础 + 多做笔记 + 多敲代码 + 多思考 + 学好英语！ 唯有努力💪 知其然 知其所以然！ 本文仅记录自己感兴趣的内...
@TOC
前言
Hello！
非常感谢您阅读海轰的文章，倘若文中有错误的地方，欢迎您指出～
自我介绍 ଘ(੭ˊᵕˋ)੭
昵称：海轰
标签：程序猿｜C++选手｜学生
简介：因C语言结识编程，随后转入计算机专业，获得过国家奖学金，有幸在竞赛中拿过一些国奖、省奖…已保研。
学习经验：扎实基础 + 多做笔记 + 多敲代码 + 多思考 + 学好英语！
唯有努力💪
知其然 知其所以然！
本文仅记录自己感兴趣的内容
题目一
内容
奇数数列求和
下面是奇数的数列：
1,3,5,7,9,…
请编写程序，输入奇数数列的项数 n，求奇数数列前 n 项的和 s。
输入格式
n
输出格式
s
输入样例
2
输出样例
4
注：题目保证 n 和 s 的值都在 long long int 类型的表示范围内。
参考Demo
#include<iostream>
using namespace std;
int main(){
long long n ;
cin >> n;
cout << n * n << endl;;
return 0;
}
题目二
内容
计科Z支书为了讲解遍历算法，专门买了三个容量分别为A,B,C的水瓶。开始时A,B水瓶为空，而C装满水。可以把水从一个水瓶倒入另一个水瓶，但每次必须把倒出的水瓶倒空或者把倒入的水瓶装满。
求当水瓶A为空的时候，C水瓶中剩下的所有水量。
输入格式:
单独的一行包括三个整数 A,B 和 C (1≤A,B,C≤40)。
输出格式:
只有一行，列出当A 是空的时候，水瓶C中装有的所有水量，按水量升序排列输出。
数字间用空格分开，同时第一个数字前面和最后一个数字后面不能留空格。
输入样例:
8 9 10
输出样例:
1 2 8 9 10
注：比如把C中的水倒出8至A，剩下的2倒入B，再把A中的水全部倒入C，则C中留有水量8。
参考Demo
#include <iostream>
#include <string.h>
#include <algorithm>
using namespace std;
int temp[1001], ont = 0;
int arr[41][41][41];
int A, B, C;
void dfs(int a, int b, int c)
{
if (!arr[a][b][c])
{
arr[a][b][c] = 1;
if (a == 0)
temp[ont++] = c;
if (a)
{
if ((a + b <= B && !arr[0][a + b][c]) || (a - B + b >= 0 && !arr[a - B + b][B][c]))
dfs(max(0, a - B + b), min(a + b, B), c);
if ((a + c <= C && !arr[0][b][a + c]) || (a - C + c >= 0 && !arr[a - C + c][b][C]))
dfs(max(0, a - C + c), b, min(C, c + a));
}
if (b)
{
if ((a + b <= A && !arr[a + b][0][c]) || (b - A + a >= 0 && !arr[A][b - A + a][c]))
dfs(min(A, a + b), max(0, b - A + a), c);
if ((c + b <= C && !arr[a][0][b + c]) || (b - C + c >= 0 && !arr[a][b - C + c][C]))
dfs(a, max(0, b - C + c), min(C, c + b));
}
if (c)
{
if ((b + c <= B && !arr[a][c + b][0]) || (C - B + b >= 0 && !arr[a][B][C - B + b]))
dfs(a, min(c + b, B), max(0, c - B + b));
if ((a + c <= C && !arr[a + c][b][0]) || !arr[A][b][c - A + a])
dfs(min(A, a + c), b, max(0, c - A + a));
}
}
}
int main()
{
cin >> A >> B >> C;
memset(temp, 0, sizeof(temp));
memset(arr, 0, sizeof(arr));
dfs(0, 0, C);
sort(temp, temp + ont);
for (int i = 0; i < ont - 1; i++)
cout << temp[i] << " ";
cout << temp[ont - 1] << endl;
return 0;
}
题目三
内容
如下的 6 x 6 的棋盘，有六个棋子（皇后）被放置在棋盘上，使得每行、每列、每条对角线(包括 两条主对角线的所有对角线)上都至多有一个棋子。
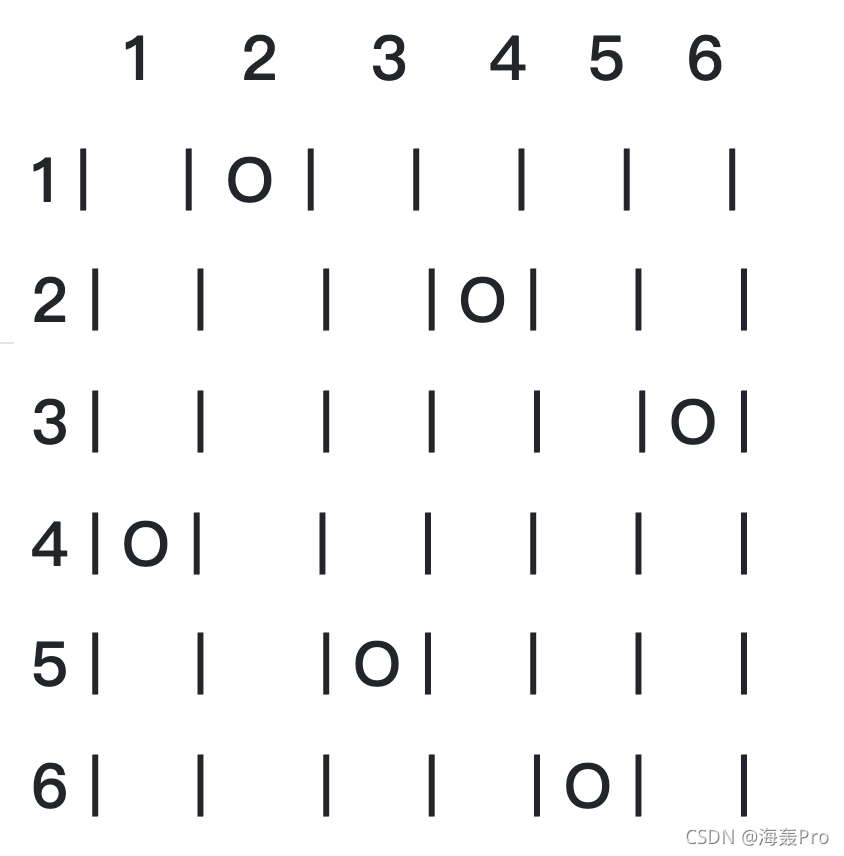
上面的布局可以用序列 2 4 6 1 3 5 来描述，第 i 个数字表示在第i 行的相应位置有一个棋子(1≤i≤6)，如下:
行号 1 2 3 4 5 6
列号 2 4 6 1 3 5
这只是跳棋放置的一个解，找出所有跳棋放置的解，并把它们以上面的序列方法输出。 解按字典顺序排列，输出前 3 个解，最后一行是解的总个数。
输入格式:
一个数字 N (6≤N≤13) 表示棋盘是 N×N 大小的。
输出格式:
前三行为前三个解，每个解的两个数字之间用一个空格隔开，第四行只有一个数字表示解的总数。
输入样例:
在这里给出一组输入。例如：
6
输出样例:
在这里给出相应的输出。例如：
2 4 6 1 3 5
3 6 2 5 1 4
4 1 5 2 6 3
4
参考Demo
#include<iostream>
#include<vector>
#include<unordered_set>
using namespace std;
vector<string> generateBoard(vector<int> &queens, int n) {
auto board = vector<string>();
for (int i = 0; i < n; i++) {
string row = string(n, '.');
row[queens[i]] = 'Q';
board.push_back(row);
}
return board;
}
void backtrack(vector<vector<string> > &solutions, vector<int> &queens, int n, int row, unordered_set<int> &columns, unordered_set<int> &diagonals1, unordered_set<int> &diagonals2) {
if (row == n) {
vector<string> board = generateBoard(queens, n);
solutions.push_back(board);
} else {
for (int i = 0; i < n; i++) {
if (columns.find(i) != columns.end()) {
continue;
}
int diagonal1 = row - i;
if (diagonals1.find(diagonal1) != diagonals1.end()) {
continue;
}
int diagonal2 = row + i;
if (diagonals2.find(diagonal2) != diagonals2.end()) {
continue;
}
queens[row] = i;
columns.insert(i);
diagonals1.insert(diagonal1);
diagonals2.insert(diagonal2);
backtrack(solutions, queens, n, row + 1, columns, diagonals1, diagonals2);
queens[row] = -1;
columns.erase(i);
diagonals1.erase(diagonal1);
diagonals2.erase(diagonal2);
}
}
}
vector<vector<string> > solveNQueens(int n) {
auto solutions = vector<vector<string> >();
auto queens = vector<int>(n, -1);
auto columns = unordered_set<int>();
auto diagonals1 = unordered_set<int>();
auto diagonals2 = unordered_set<int>();
backtrack(solutions, queens, n, 0, columns, diagonals1, diagonals2);
return solutions;
}
int main(){
int n ;
cin >> n;
vector<vector<string> > a = solveNQueens(n);
for(int i = 0; i < 3; ++i) {
vector<int> temp(n);
for(int j = 0; j < a[i].size(); ++j){
temp[j] = a[i][j].find('Q') + 1;
}
for(int k = 0; k < temp.size() - 1; ++ k) {
cout << temp[k] << " ";
}
cout << temp[temp.size() - 1] ;
cout << endl;
}
cout << a.size() << endl;
return 0;
}
暴力取巧：最后两个测试用例一个是n=12一个是n=13，直接return即可
题目四
内容
由相同数量的左括号’(‘和右括号’)'构成的字符串，只需要将一定长度（可以为0）的前缀移动到字符串的末尾，就可以使其中的左右括号匹配成功，即成为括号语句。在这里，我们不用数学方法去证明该命题的正确性，而是编程求出所有可行的前缀长度。
输入格式:
- 输入在一行中给出由’(‘和’)'构成的字符串，长度不超过 。
- 题目保证字符串中左右括号的数量相同。
输出格式:
- 在一行中输出所有可行的前缀长度，按升序排列。
- 数值间用空格分开，末尾的值后面没有空格。
输入样例:
(()))))()(())((()))()(((
输出样例:
7 9 13 19 21
注：上述长度的前缀各自移动到末尾后得到的括号语句如下：
长度7： ()(())((()))()((((()))))
长度9： (())((()))()((((()))))()
长度13：((()))()((((()))))()(())
长度19：()((((()))))()(())((()))
长度21：((((()))))()(())((()))()
参考Demo - 1
#include <cstdlib>
#include <iostream>
#include <queue>
#include <stack>
using namespace std;
bool isQTrue(vector<char>& q) {
if (q.size() == 0) {
return true;
}
stack<char> stack;
for (int i = 0; i < q.size(); i++) {
char c = q[i];
if (c == '(') {
stack.push(c);
}
if (c == ')') {
if (stack.empty()) {
return false;
}
char one = stack.top();
if (c == ')' && one != '(') {
return false;
}
stack.pop();
}
}
if (!stack.empty()){
return false;
}
return true;
}
int main()
{
vector<char> q;
int flag = 0;
string s;
cin >> s;
for (int i = 0; i < s.length(); i++) {
q.push_back(s[i]);
}
if (isQTrue(q)) {
cout << 0;
flag = 1;
}
for (int i = 1; i < s.length(); i++) {
q.push_back(q[0]);
vector<char>::iterator k = q.begin();
q.erase(k);
if (isQTrue(q)) {
if (flag == 1) {
cout << " ";
cout << i;
}
else {
cout << i;
flag = 1;
}
}
}
return 0;
}
参考Demo - 2
#include <iostream>
#include <algorithm>
#include<unordered_map>
#include <vector>
#include <stack>
using namespace std;
bool isValid(string s) {
if(s == ""){
return true;
}
vector<char> stack;
stack.push_back(s[0]);
for(int i=1; i<s.size(); i++){
if(stack.empty() == true){
stack.push_back(s[i]);
}else if(s[i] - stack.back() == 1 || s[i] - stack.back() == 2){
stack.pop_back();
} else {
stack.push_back(s[i]);
}
}
return stack.empty();
}
int main()
{
string s;
cin >> s;
int n = s.length();
vector<int> ans;
for (int i = 0; i < n; ++i)
{
string ss= s;
string s1 = ss.substr(0, i);
ss = ss + s1;
ss = ss.substr(i, n);
if (isValid(ss))
{
ans.push_back(i);
}
}
for(int i = 0; i < ans.size()- 1; ++i) {
cout << ans[i] << " ";
}
cout << ans[ans.size()- 1] << endl;
return 0;
}
题目五
内容
合并排序是经典的排序算法，主要包含两个任务：
一、 把两个子序列（数组）分别按从大到小的顺序排序。
二、合并两个子序列，要求 (1) 不得改变同一个子序列中的数值间的先后顺序（间距可变）；(2) 合并后的序列字典序必须最大（与满足(1)的其它合并结果相比）。
本来刘大师想把合并排序加入考试题目，但遭到G队长的强烈反对，认为两个任务太多，学生"鸭梨"大，需要"减负"。经过激烈的争论(dou)，最终说(gan)不过队长的刘大师只得把任务一去掉，留下第二个任务让学生完成。
输入格式:
- 输入第一行给出两个正整数 ，分别表示两个序列的长度。
- 接下来两行，第一行含N个正整数，用空格隔开
- 第二行包括M个正整数。保证所有数值都在区间[1,1000]以内。
输出格式:
- 输出一行整数，即两个序列合并后的结果。
- 数值间用空格分开，末尾的数值后面没有空格。
输入样例1:
4 2
5 7 8 3
6 4
输出样例1:
6 5 7 8 4 3
输入样例2:
5 4
5 4 7 4 3
6 4 4 6
输出样例2:
6 5 4 7 4 4 6 4 3
参考Demo
#include<iostream>
#include<algorithm>
using namespace std;
int main(){
int a,b;
cin>>a>>b;
int num_a[a];
int num_b[b];
for(int i=0;i<a;i++){
cin>>num_a[i];
}
for(int i=0;i<b;i++){
cin>>num_b[i];
}
//string res;
int num_ans[a+b];
int index_1=0,index_2=0;
int now_z=0;
while(index_1<a && index_2<b){
if(num_a[index_1]<num_b[index_2]){
num_ans[now_z]=num_b[index_2];
++index_2;
now_z++;
}
else if(num_a[index_1]>num_b[index_2]){
num_ans[now_z]=num_a[index_1];
++index_1;
now_z++;
}
else {
int i1=index_1,i2=index_2;
while(i1<a && i2<b && num_a[i1]==num_b[i2]){
++i1;
++i2;
}
if(i1==a || num_a[i1]<num_b[i2]){
num_ans[now_z]=num_b[index_2];
++index_2;
now_z++;
}
else{
num_ans[now_z]=num_a[index_1];
++index_1;
now_z++;
}
}
}
if(index_1==a){
while(index_2<b){
num_ans[now_z]=num_b[index_2];
now_z++;
index_2++;
}
}
else{
while(index_1<a){
num_ans[now_z]=num_a[index_1];
now_z++;
index_1++;
}
}
for(int i=0;i<a+b;i++){
if(i==a+b-1){
cout<<num_ans[i];
}
else{
cout<<num_ans[i]<<" ";
}
}
cout<<endl;
}
注：一次课程在线测试的个人记录
结语
文章仅作为个人学习笔记记录，记录从0到1的一个过程
希望对您有一点点帮助，如有错误欢迎小伙伴指正
【版权声明】本文为华为云社区用户原创内容，未经允许不得转载，如需转载请自行联系原作者进行授权。如果您发现本社区中有涉嫌抄袭的内容，欢迎发送邮件进行举报，并提供相关证据，一经查实，本社区将立刻删除涉嫌侵权内容，举报邮箱：
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者
评论（0）