【课程作业】西瓜书 机器学习课后习题 : 第六章
【摘要】 @TOC 简介Hello!非常感谢您阅读海轰的文章,倘若文中有错误的地方,欢迎您指出~ ଘ(੭ˊᵕˋ)੭昵称:海轰标签:程序猿|C++选手|学生简介:因C语言结识编程,随后转入计算机专业,获得过国家奖学金,有幸在竞赛中拿过一些国奖、省奖…已保研学习经验:扎实基础 + 多做笔记 + 多敲代码 + 多思考 + 学好英语! 唯有努力💪 本文仅记录自己感兴趣的内容 说明作业要求:每章从课后习题中选...
@TOC

简介
Hello!
非常感谢您阅读海轰的文章,倘若文中有错误的地方,欢迎您指出~
ଘ(੭ˊᵕˋ)੭
昵称:海轰
标签:程序猿|C++选手|学生
简介:因C语言结识编程,随后转入计算机专业,获得过国家奖学金,有幸在竞赛中拿过一些国奖、省奖…已保研
学习经验:扎实基础 + 多做笔记 + 多敲代码 + 多思考 + 学好英语!
唯有努力💪
本文仅记录自己感兴趣的内容
说明
作业要求:每章从课后习题中选取3道题做就可以了
答案来源:题目的解答过程来自于网络,依据个人所学进行了一些修改、总结
仅供参考
6.1
试证明样本空间中任意点x到超平面(w,b)的距离为式(6.2)

6.2
试使用LIBSVM,在西瓜数据集3.0α上分别用线性核和高斯核训练一个SVM,并比较其支持向量的差别。
答:实验代码如下:
from sklearn import svm
X=[
[ 0.697, 0.46 ],
[ 0.774, 0.376],
[ 0.634, 0.264],
[ 0.608, 0.318],
[ 0.556, 0.215],
[ 0.403, 0.237],
[ 0.481, 0.149],
[ 0.437, 0.211],
[ 0.666, 0.091],
[ 0.243, 0.267],
[ 0.245, 0.057],
[ 0.343, 0.099],
[ 0.639, 0.161],
[ 0.657, 0.198],
[ 0.36 , 0.37 ],
[ 0.593, 0.042],
[ 0.719, 0.103]
]
y=[1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0]
plt.figure(figsize=(18,6))
for i in range(0, len(X)):
plt.subplot(1,3,1)
if y[i] == 1:
plt.scatter(X[i][0],X[i][1],c='r',marker='*')
else:
plt.scatter(X[i][0],X[i][1],c='g',marker='*')
print("-"*20+"线性核"+"-"*20)
clf1=svm.SVC(C = 1,kernel='linear')
print("交叉验证评分",cross_val_score(clf1,X,y,cv=5,scoring='accuracy').mean())
clf1.fit(X,y)
print("支持向量数目:",clf1.n_support_.sum())
print("支持向量:")
print(clf1.support_vectors_)
for i in X:
res=clf1.predict(np.array(i).reshape(1, -1))
plt.subplot(1,3,2)
if res > 0:
plt.scatter(i[0],i[1],c='r',marker='*')
else :
plt.scatter(i[0],i[1],c='g',marker='*')
print("-"*20+"高斯核"+"-"*20)
clf2=svm.SVC(C=1,kernel='rbf')
print("交叉验证评分",cross_val_score(clf2,X,y,cv=5,scoring='accuracy').mean())
clf2.fit(X,y)
print("支持向量数目",clf2.n_support_.sum())
print("支持向量:")
print(clf2.support_vectors_)
for i in X:
res=clf2.predict(np.array(i).reshape(1, -1))
plt.subplot(1,3,3)
if res > 0:
plt.scatter(i[0],i[1],c='r',marker='*')
else :
plt.scatter(i[0],i[1],c='g',marker='*')
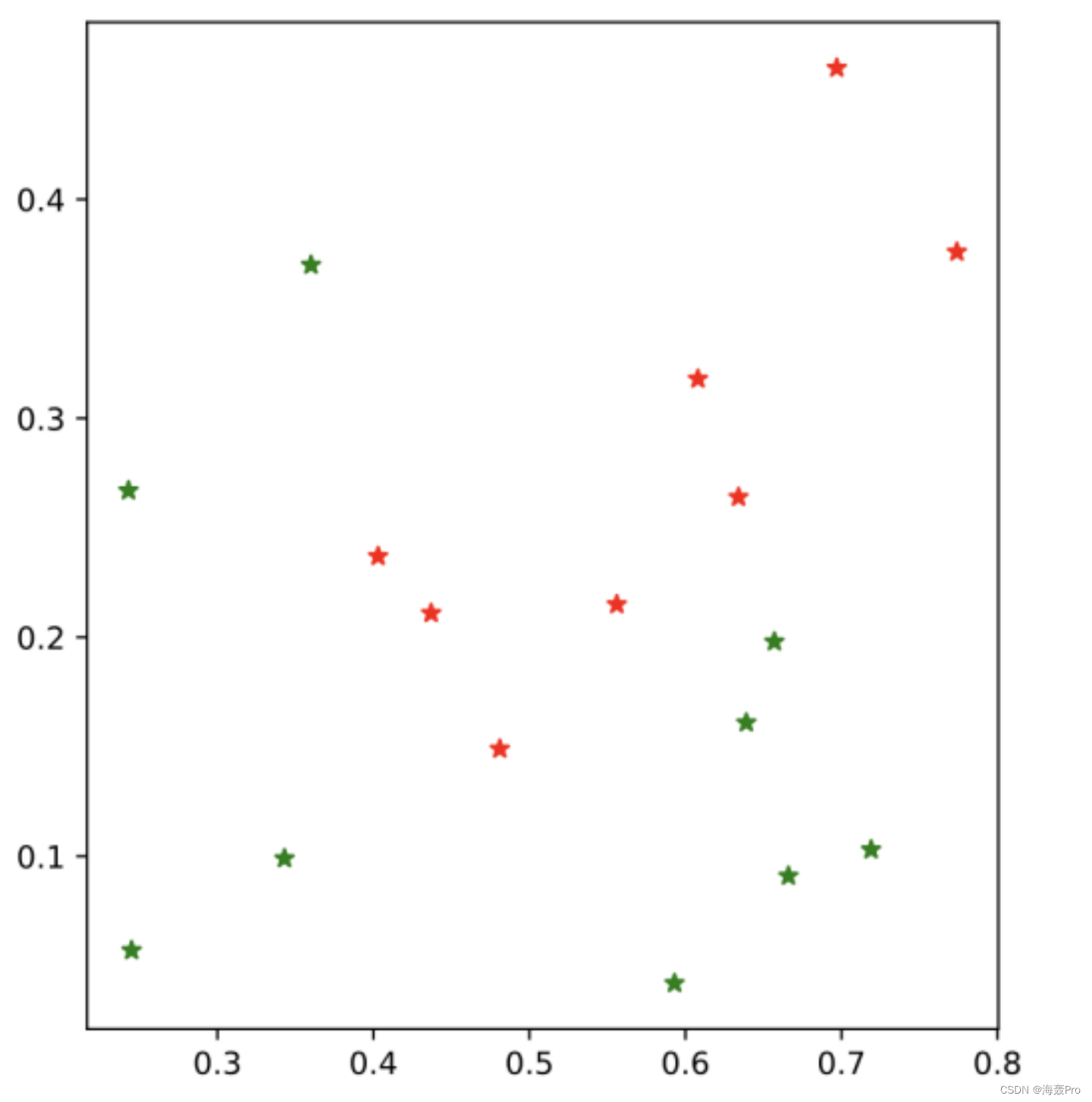
西瓜数据集3.0α的可视化,其中绿色代表好瓜,红色代表坏瓜
分别使用线性核与高斯核训练一个SVM的实验结果
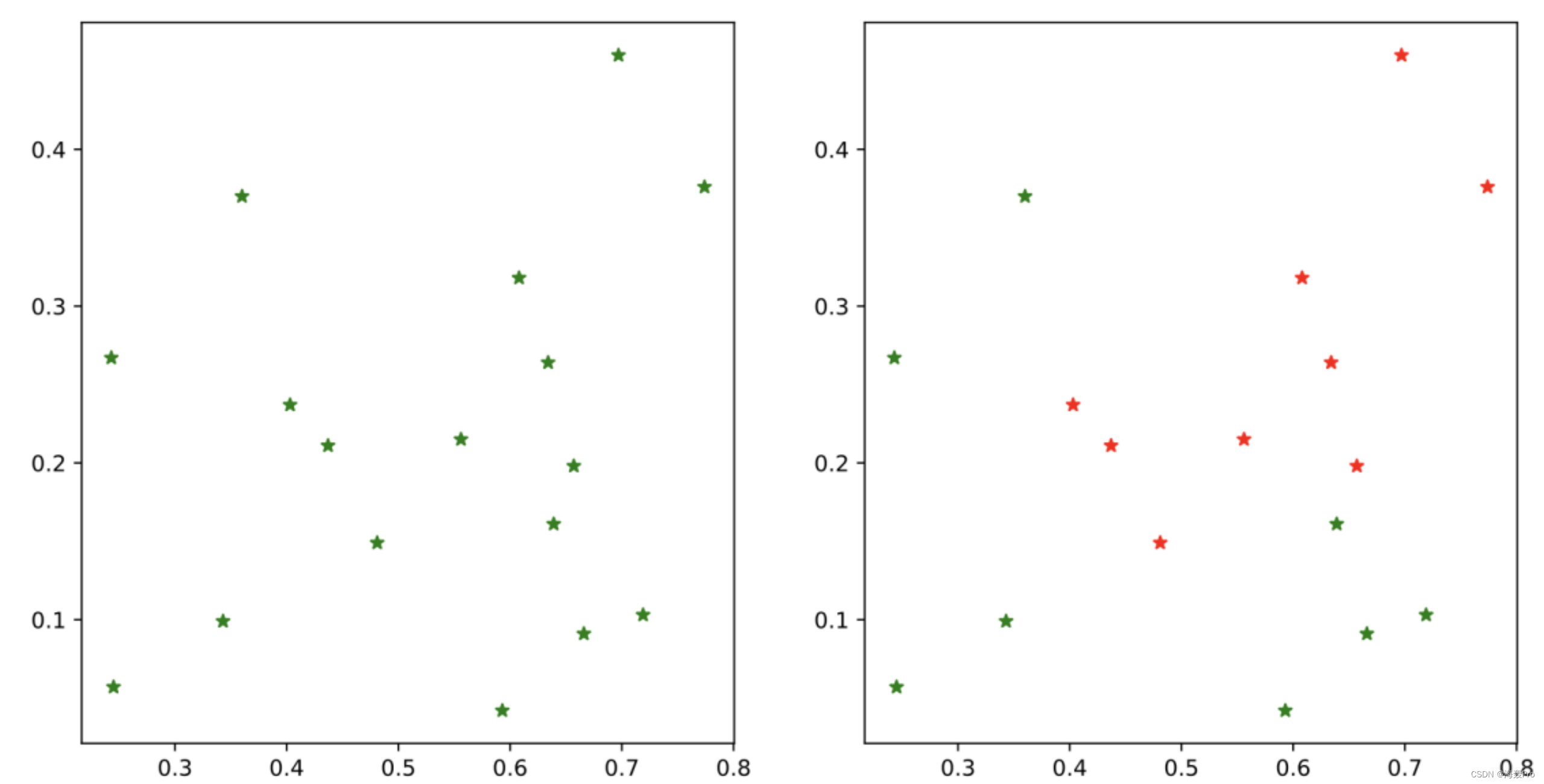
实验分析:当惩罚系数C都为1时,采用线形核的svm分类效果非常不好,高斯核表现较好,支持向量数理也多于线性核,随着C的不断增大,线性核的效果开始变好
6.6
试析SVM对噪声敏感的原因
答:SVM的目的是求出与支持向量有最大化距离的直线,以每个样本为圆心,该距离为半径做圆,可以近似认为圆内的点与该样本属于相同分类。如果出现了噪声,那么这个噪声所带来的错误分类也将最大化,所以SVM对噪声是很敏感的。
结语
文章仅作为个人学习笔记记录,记录从0到1的一个过程
希望对您有一点点帮助,如有错误欢迎小伙伴指正

【版权声明】本文为华为云社区用户原创内容,未经允许不得转载,如需转载请自行联系原作者进行授权。如果您发现本社区中有涉嫌抄袭的内容,欢迎发送邮件进行举报,并提供相关证据,一经查实,本社区将立刻删除涉嫌侵权内容,举报邮箱:
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者


评论(0)