二叉树的下一个结点 _二叉搜索树的第k个节点

二叉树

二叉树的下一个结点

二叉树的下一个结点


/*
public class TreeLinkNode {
    int val;
    TreeLinkNode left = null;
    TreeLinkNode right = null;
    TreeLinkNode next = null;

    TreeLinkNode(int val) {
        this.val = val;
    }
}
*/
//方法一:中序遍历,保存节点!
// import java.util.*;
// public Solution {
//     ArrayList<TreeLinkNode> result = new ArrayList<>();
//     public void inOrder(TreeLinkNode root){
//         if(root==null){
//             return;
//         }
//         inOrder(root.left);
//         result.add(root);
//         inOrder(root.right);
//     }
//     public TreeLinkNode GetNext(TreeLinkNode pNode) {
//         //找到根节点!
//         TreeLinkNode pcur = pNode;
//         while(pcur.next!=null){
//             pcur = pcur.next;
//         }
//         //中序遍历
//         inOrder(pcur);
//         for(int i = 0;i<result.size()-1;i++){
//             if(pNode==result.get(i)){
//                 return result.get(i+1);
//             }
//         }
//         return null;
//     }
// }
//方法二:分类讨论!
public class Solution {
    public TreeLinkNode GetNext(TreeLinkNode pNode) {
        //分类讨论:
        //1.节点有右子树,右子树的最左节点就是结果!
        //2.节点没有右节点,并且该父节点的右节点不是该节点,节点是父节点的左节点 结果就是父节点!
        //3.节点没有右节点,并且该父节点的右节点就是本身,节点是父节点的右节点,结果就是根节点!
        // 1).有可能是左子树的最后一个节点,那么久返回根节点即可!
        // 2).右子树最后一个节点,返回null!
        // 使用 ppar.next.right==ppar判断区分这两种情况!
        
        // 情况一
        if(pNode.right != null) {
            TreeLinkNode rchild = pNode.right;
            // 一直找到右子树的最左下的结点为返回值
            while(rchild.left != null) rchild = rchild.left;
            return rchild;
        }
         
        // 情况二
        if(pNode.next != null && pNode.next.left == pNode) {
            return pNode.next;
        }
         
        // 情况三
        if(pNode.next != null) {
            TreeLinkNode ppar = pNode.next;
            // 沿着左上一直爬树，爬到当前结点是其父节点的左自己结点为止
            while(ppar.next != null && ppar.next.right == ppar){
                //ppar.next.right 区别该节点是否为右子树最后一个节点或者是左子树最后一个节点!
                //1.左子树最后一个节点: 左子树根节点 ppar.next.right!=ppar 返回 根!
                //2.右子树最后一个节点: 右子树根节点 ppar.next.right==ppar 返回 null!
                ppar = ppar.next;
            }
            return ppar.next;
        }
        return null;
    }
}

二叉搜索树的第k个节点

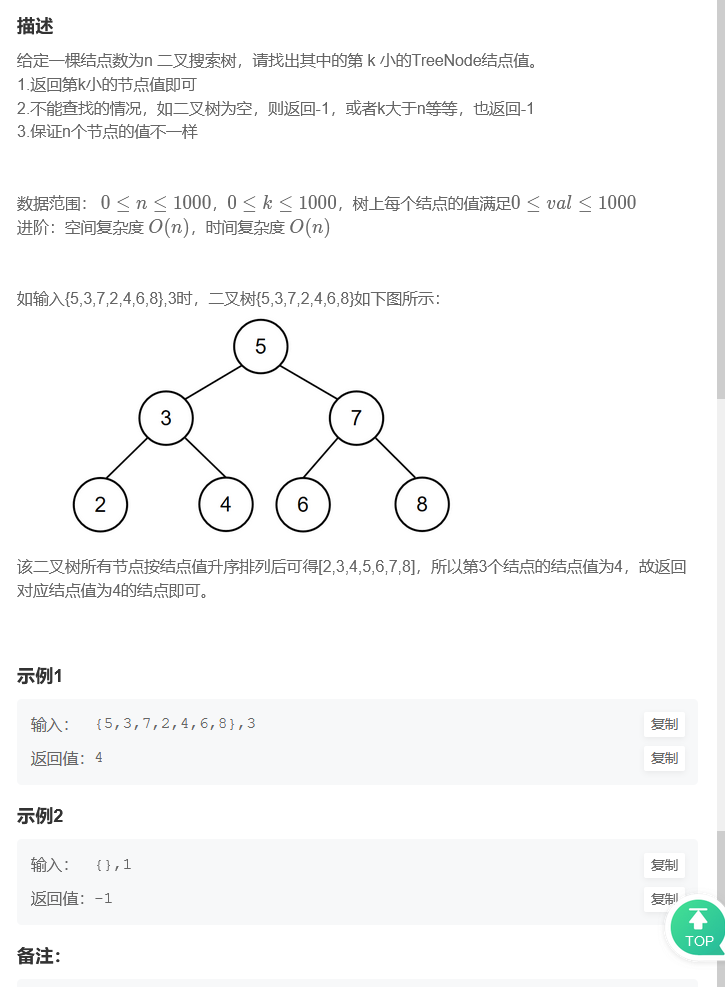
//1.用数组保存所有节点值!
     private void Inord(ArrayList<Integer> result,TreeNode root){
         if(root==null) return;
         Inord(result,root.left);
         result.add(root.val);
         Inord(result,root.right); 
     }
    public int KthNode (TreeNode proot, int k) {
        // write code here
        //二叉搜索树 中序遍历 得到就是有序递增序列!
        if(proot==null||k<1) return -1;//为空或者k有误
        ArrayList<Integer> result = new ArrayList<>();
        Inord(result,proot);
        if(k>result.size()) return -1;//k越界!
        return result.get(k-1);
    }
    //优化,通过一个成员变量节点保存该节点值,一个成员变量记录第几个即可
    private TreeNode res = null;//记录节点
    private int count = 0;//记录当前递归次数!
      private void Inord(TreeNode root,int k){
         if(root==null||count>k)//count已经大于k还未找到||已经递归结束!
            return;
         Inord(root.left,k);
          count++;//递归次数加一!(这里的k是从1开始)
        if(count==k) res = root;//找到了该节点!
         Inord(root.right,k); 
     }
    public int KthNode (TreeNode proot, int k) {
        // write code here
        //二叉搜索树 中序遍历 得到就是有序递增序列!
        Inord(proot,k);
        if(res==null)return -1;
        return res.val;
    }
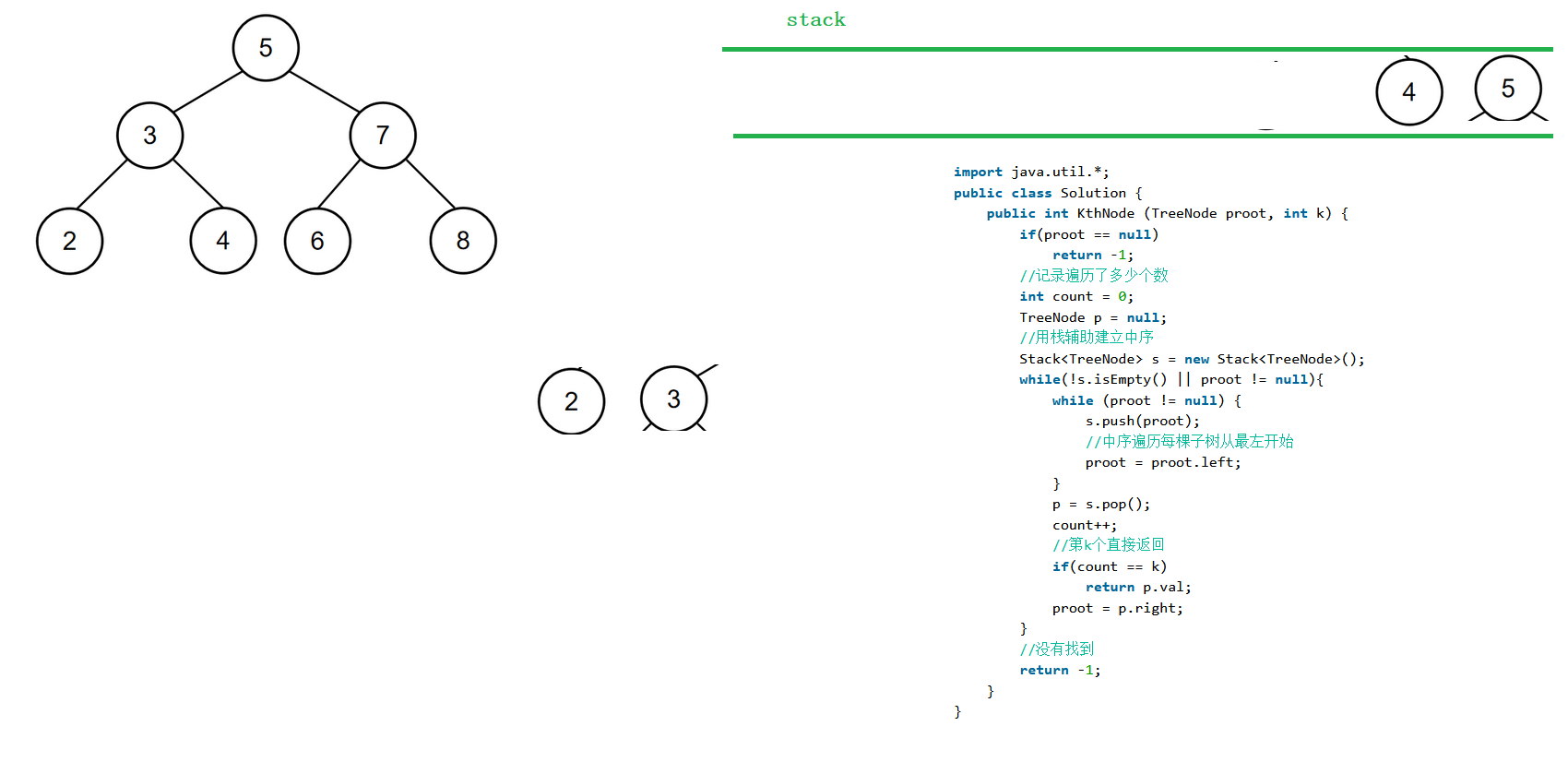
    //方法二:利用栈中序非递归!
       public int KthNode (TreeNode proot, int k) {
           if(proot==null) return -1;
           //通过栈结构辅助!
           //1.一直入左节点,直到左子树为空!
           //2.如果没有左子树节点入栈了那就出栈,
           //然后将出栈节点的右节点入栈(这里就实现了左中右)
           //循环执行1,2操作,记录出栈次数count,直到 k==count 返回节点的va
           Stack<TreeNode> stack = new Stack<>();
           TreeNode p = null;//记录出栈节点!
           int count = 0;//记录出栈次数(前n个节点!)
           while(!stack.isEmpty()||proot!=null){
                //栈不为空或者proot不会空说明没有遍历结束!
               while(proot!=null){//将左节点一直入栈!
                   stack.push(proot);
                   proot = proot.left;
               }
               //左节点全部入栈!
               //出栈,
               p = stack.pop();
               count++;
               if(count==k){//说明找到了第k个!
                   return p.val;
               }
               if(count>k) return -1;//找不到了!
               proot = p.right;//将proot指向右子树!
           }
           return -1;
    }