【图像插值】基于matlab稀疏拉普拉斯滤波器图像插值【含Matlab源码 2055期】

一、插值简介

插值是根据抽样函数或信号估计连续位置的数值，或者是根据一系列离散采样点重构出原始的连续函数。在图像几何变换中，经过几何变换后的图像像素可能在原始图像中并没有对应的像素点，那么，在目标图像中这些没有对应点的像素灰度值该如何取值呢？通过图像的插值。图像插值对于目标图像像素点的任何连续位置，都可以获得一个较为精确的插值。而插值函数需要尽可能的保留图像的细节，并且尽可能的少引入人为噪声。

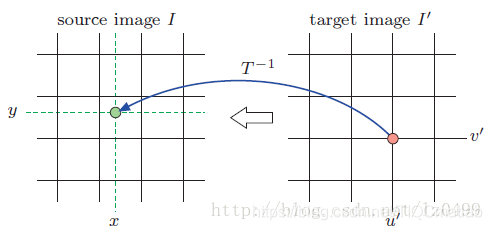
目标—原始图像的映射。对于目标图像中的每一个离散的像素位置(u,v)，通过逆变换函数，对应于原始图像中连续的位置(x,y)。目标图像中的I(u,v)像素灰度值可以根据原始图像坐标(x,y)的某些邻域插值获得。

1 一维插值
一维平面中一些简单的插值算法，是根据离散函数g（u）（u属于整数），插值生成任意连续位置对应的数值。
最近邻插值
在所有插值算法中，最简单的就是最近邻插值算法。最近邻插值算法中，对连续坐标x向下取整，得到与之最近的整数u0，再根据离散采样函数g(u0)作为连续坐标x的估算值。即：

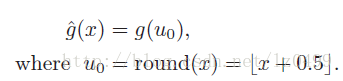
2 线性插值
另一种比较简单的插值算法是线性插值。线性插值的估算值是根据最近两个采样点的采样值g(u0)和g(u0+1)，u0为x向下取整，根据采样点离连续x的距离进行加权求和，得到其最终的估计值。

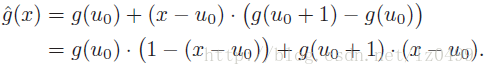
类似这种线性插值：已知数据 (x0, y0) 与 (x1, y1)，要计算 [x0, x1] 区间内某一位置 x 在直线上的y值（反过来也是一样，略）：
上面比较好理解吧，仔细看就是用x和x0，x1的距离作为一个权重，用于y0和y1的加权。假设x倾向靠近x1，那么最终计算出来的y值也是应该倾向靠近于y1,；故其权重应该比较大，取其权重值应该为x2-x，；假设x倾向靠近X2，那么计算出来的Y也是应该更靠近于y2,其权重应该取其较大值x-x1。即不管X是倾向靠近x1,还是倾向靠近x2，上式线性插值公式总是成立。而双线性插值本质上就是在两个方向上做线性插值。
两种一维插值如下图所示：

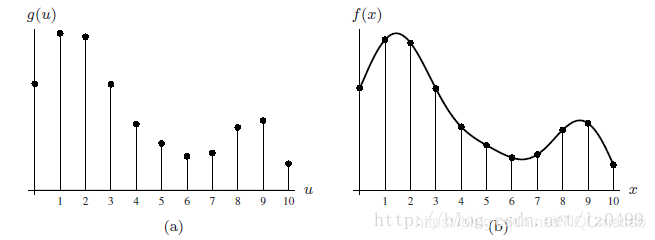
给定的离散函数g（u）（a）,插值目标是估算其原始函数f(x)在任意连续坐标位置的数值,x属于实数 。（b）

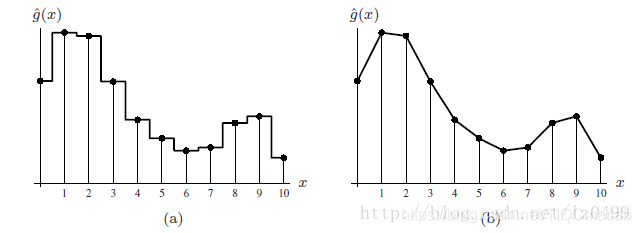
最近邻插值算法（a）和线性插值算法（b）

3 理想的插值
显然，上述简单的线性插值并不能准确的估算原始的连续函数。当原始连续函数并不知晓的情况下，如何根据离散的采样点或采样函数更为准确的估算其原始的连续函数呢？初看起来是没有一点头绪，因为离散的采样函数g(u)可能从任何在离散采样位置有确定值的连续函数f(x)中采样获得。
但是，我们如果从频域角度尝试解决这个问题，那么这个问题将豁然开朗。倘若原始连续信号f(x)根据抽样定理进行离散化，那么函数f(x)有频带限制的特性-----不可能包含任意高于采样频率一半的频率的信号。这就意味着，重构出来的信号只包含某一限制区域的频率。
数字信号中所有频率只与采样频率有关。假设我们以t = 1为采样间隔，采样频率即为:

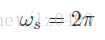
那么，根据抽样定理可知，原始信号最大的频率为wmax=π,，为了分离傅里叶频谱（周期性的）中对应的频谱范围-wmax………. wmax，我们把频谱函数G(w)乘以宽度为正负Pid的一个方形窗口函数，即

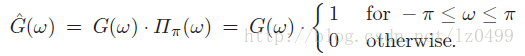
这被称之为理想的低通滤波。它把所有频率高于π的信号切除，只保留频率小于等于π以内的信号。根据卷积特性，如果两个原始函数服从线性卷积，那么它们卷积的傅里叶变换结果即为两个原始函数频谱函数的点积，即：


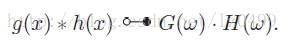
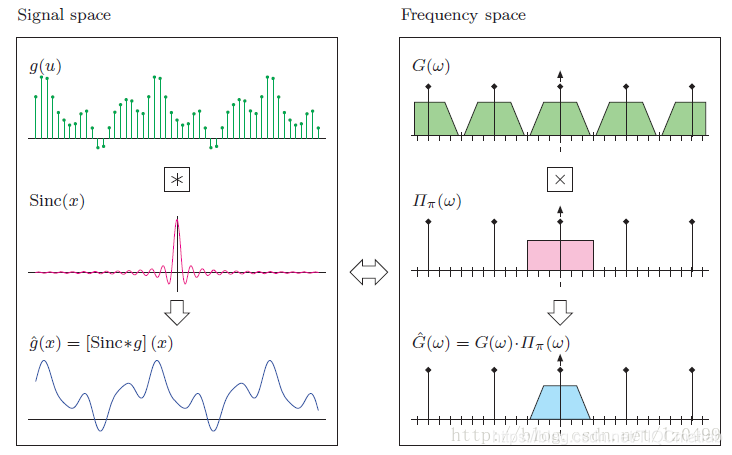
离散信号的插值原理：时域和频域之间的关系
由此，我们可以得出，在时域中对应的窗口频谱函数为：

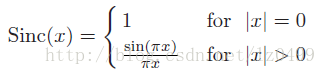
理论上来说，对于重构符合抽烟定理的连续信号，Sinc(x)是一个理想的插值函数。为了利用离散函数g(u) 计算任意位置x0的插值,Sinc函数必须移位x0,之后乘以离散函数的所有离散值，其最后的插值为所有乘积之和。假设g(u) 和Sinc（x）符合线性卷积，那么插值之后的值，可以表示为：

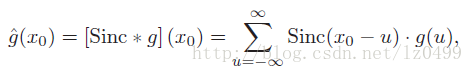
由插值公式可知，利用离散函数g(u)计算任意位置x0的插值时，不仅仅只是利用采样点周围的领域各点，而是利用的离散函数中无限多个采样点，每个采样的权重为采样点与插值点x0之间的距离函数计算而得（距离函数为1/Pi*(x0-u))
如果连续函数符合抽样定理，那么它能够通过Sinc(x)函数进行插值，从离散的信号中准确的重构出来。如下图所示：

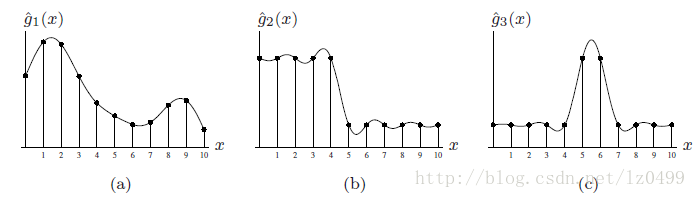
Sinc(x)在不同类型信号中进行插值。重构的函数(a),符合抽c频率限制。阶跃函数（b）和脉冲函数©通过Sinc(x)进行插值时，将产生振铃效应。

4 通过卷积进行插值
如前所述，重构连续信号可以描述为一种线性卷积的操作。因此，我们可以把插值看作为离散函数g(u)和某一连续插值核函数做卷积，即

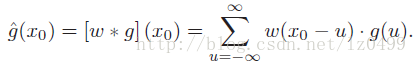
插值函数Sinc(x)显然是插值核函数的一种特例。相类似的，对于一维函数的最近邻插值运算中，其插值核函数可以表示为：

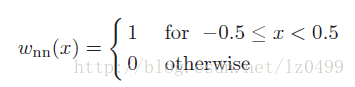
对于一维函数中的线性插值运算总，其插值核函数可以表示为：


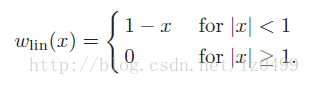
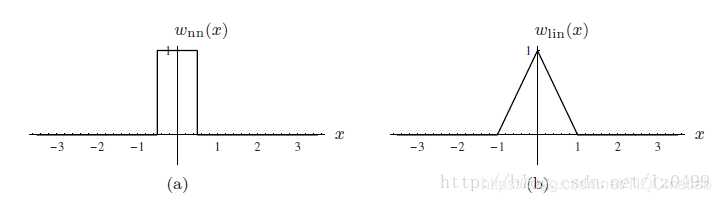
最近邻插值卷积核函数（a），线性插值卷积核函数（b）

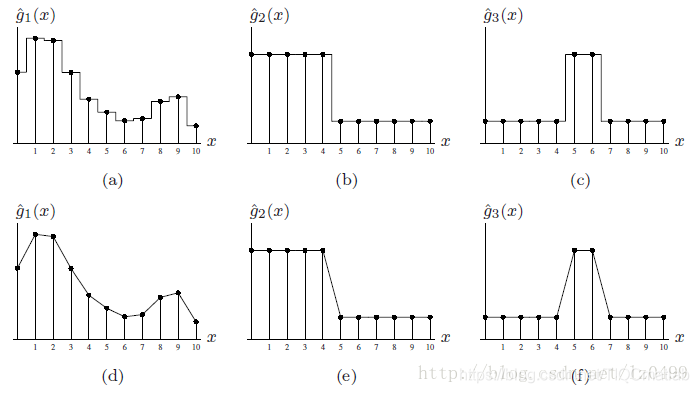
最近邻插值示例（a-c），线性插值示例（d-f）

5 三次多项式插值
由于Sinc(x)函数的无限性和其衰减所带来的振铃效应，在实际应用中，我们并不使用Sinc（x）作为其插值核函数。因此，实际应用中常常使用Sinc函数的截断版本或Sinc函数的近似函数作为插值核函数。三次多项式插值一种常用的近似于Sinc截断版本的卷积核函数，其卷积核函数是由三次多项式组成：

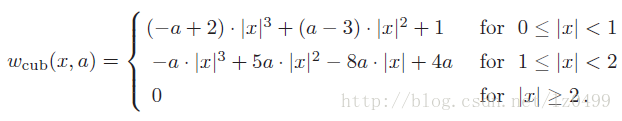
实际应用当中，常常使用a为1的三次多项式组成的卷积函数。即上式改写为：

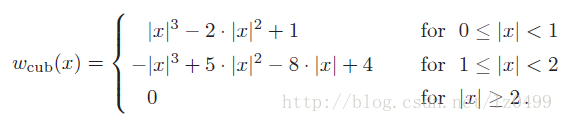
与Sinc函数相反，三次多项式插值卷积核函数取值范围比较小，因此很方便计算。由于当x>=2的时候，其权重值为0，因此，在插值计算的时候只考虑一下四点即可：

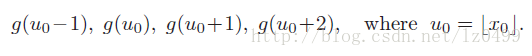
因此，一维立方插值函数可以表示为

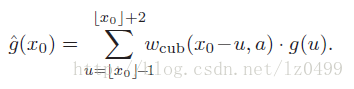
5 二维插值
上述各个章节中，只是考虑了从一维离散信号中进行插值运算。而数字图像是二维离散信号，对二维离散信号进行插值运算类似于一维插值运算。在二维信号中，理想的插值函数为：

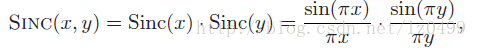
同一维插值中Sinc函数特性一样，在二维插值应用中，我们并不是使用SINC作为插值函数，而是使用类似一维中的其他插值函数。比如最近邻插值函数、线性插值函数、三次多项式插值函数等。
二维最近邻插值
对于给定的连续坐标点（x0,y0）,与其最近的像素坐标即为分别对x坐标方向和y坐标方向进行取整。即

二维最近邻插值中，其卷积核函数可以表示为：

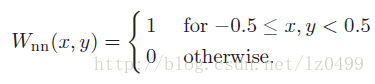
二维最近邻插值中，插值生成的图像将产生比较明显的马赛克，效果不是很好。

二、部分源代码

clear all
close all
% read image
rgb = imread(‘lena.tiff’);
figure
subplot(211)
imshow(rgb,[]);title(‘原图’)
% cast to double
rgb = double(rgb);
% mosaic pattern
% G R …
% B G …
% : :
pattern = ‘grbg’;
% demosaicking
sigma = 1.4;
rgb_dem = demosaick(rgb, pattern, sigma);
% save image
imwrite(uint8(rgb_dem), ‘lena_MLRI.tiff’);
% show image

subplot(212)
imshow(rgb_dem/255);title(‘插值图’)
% calculate PSNR and CPSNR
psnr = impsnr(rgb, rgb_dem, 255, 10);
cpsnr = imcpsnr(rgb, rgb_dem, 255, 10);

% print PSNR and CPSNR
fprintf( sprintf( ‘Red:%f\n’, psnr(1) ) );
fprintf( sprintf( ‘Green:%f\n’, psnr(2) ) );
fprintf( sprintf( ‘Blue:%f\n’, psnr(3) ) );
fprintf( sprintf( ‘CPSNR:%f\n’, cpsnr ) );

三、运行结果

四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 王瑞霞,彭国华,郑红婵.拉普拉斯稀疏编码的图像检索算法[J].计算机科学. 2014,41(08)

3 备注
简介此部分摘自互联网，仅供参考，若侵权，联系删除

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/126512882