三角形_猴子分桃_mkdir

三角形

三角形

在线OJ注意输入输出 格式和范围!

这里的范围超过了 int和long的大小!!!

所以我们要通过字符串或者BigInteger进行计算!

BigInteger类

表示范围: -2 ^Integer.MAX_VALUE （排他） ~ +2 ^ Integer.MAX_VALUE （排他）

包名:java.math.BigInteger

BigDecimal类 对应更大精度的浮点型(超过16位)计算!!!


第2个构造方法,会导致double的精度丢失!

import java.util.*;
import java.math.BigInteger;//导入包 java.math!!!
public class Main{
    public static void main(String[] args){
        Scanner sc = new Scanner(System.in);
        while(sc.hasNext()){
            BigInteger[] arr = new BigInteger[3];
            for(int i = 0;i<arr.length;i++){
                arr[i] = sc.nextBigInteger();
            }
            Arrays.sort(arr);
            //注意:BigInteger 不可以直接相加,要使用 add 方法进行相加!
            //通过 compareTo方法进行比较!
            //arr[0]+arr[1]>arr[2] error!!!
            if(arr[0].add(arr[1]).compareTo(arr[2])>0){
                //两边之和大于第三边
                System.out.println("Yes");
            }else{
                 System.out.println("No");
            }
        }
    }
}

猴子分桃

链接：https://www.nowcoder.com/questionTerminal/480d2b484e1f43af8ea8434770811b4a
来源：牛客网

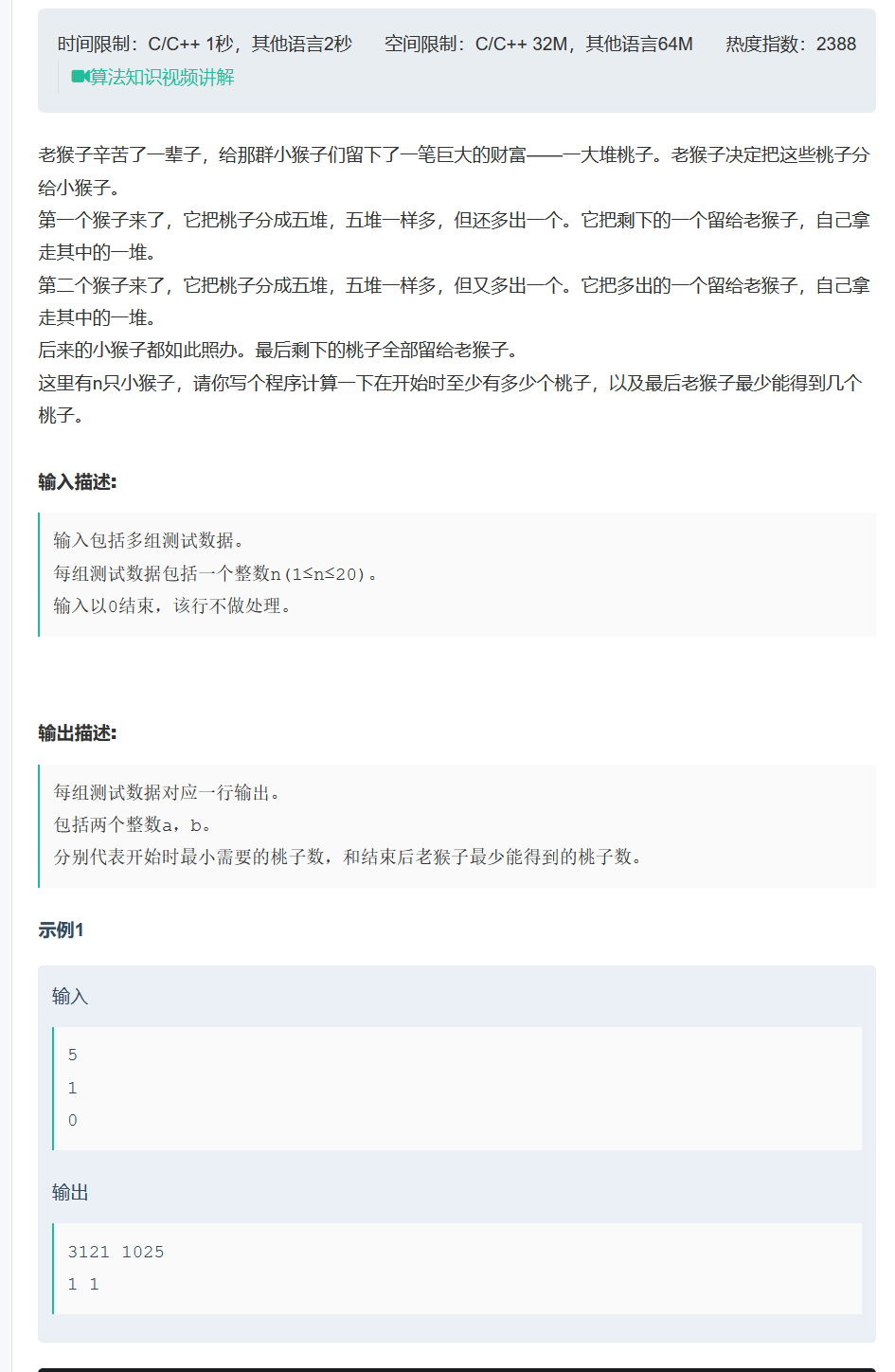
题目分析:

从题目中来看，小猴子每次将桃子均分为 5 堆时都会多出来 1 个，所以为了方便计算，我们在最开始时就借给猴子们 4 个桃子，这样的话，每次都可以刚好均分为 5 堆!

假设在开始时就有 X 个桃子，借给猴子们 4 个后，此时就一共有 X+4 个桃子。
　　　　当第一只小猴子来时，它将 X+4 个桃子均分为 5 堆后，拿走 (X+4)*(1/5) 个，剩余 (X+4)*(4/5) 个桃子。在这里，有人可能会有疑问：给老猴子的那个桃子去哪里呢？其实，小猴子拿的那一部分就包括了这一个桃子，并且小猴子也没有多得桃子，它实际上得到的桃子数为 (X+4)*(1/5) - 1 = (X-1)*(1/5) ，这和在不借给它们 4 个桃子的情况下得到的数量是一样的，不过此时剩余的桃子数相较于之前多了 (X+4)*(4/5) - (X-1)*(4/5) = 4 个，但这样就恰巧保证了下一只小猴子分桃时，也能刚好均分为 5 堆。由此可见，所有的小猴子都不会多得桃子，老猴子也不会少得桃子，并且每次小猴子都能刚好将桃子均分为 5 堆，而借给的那 4 个桃子每次都在剩余的那部分里，最后去除即可。
　　　　当第二只小猴子来时，它将 (X+4)*(4/5) 个桃子均分为 5 堆后，拿走 (X+4)*(4/5)*(1/5) 个，剩余 (X+4)*(4/5)^2 个桃子。
　　　　当第三只小猴子来时，它将 (X+4)*(4/5)^2 个桃子均分为 5 堆后，拿走 (X+4)*(4/5)^2*(1/5) 个，剩余 (X+4)*(4/5)^3 个桃子。
　　　　…
　　　　依次类推，当第 n 只小猴子（最后一只小猴子）来时，它将 (X+4)*(4/5)^(n-1) 个桃子均分为 5 堆后，拿走 (X+4)*(4/5)^(n-1)*(1/5) 个，剩余 (X+4)*(4/5)^n 个桃子。

为了满足题目最后的要求，也就是要保证最后剩余的桃子数最少且为整数，那么当 X+4 = 5^n 时，刚好满足要求，此时可得出：
（1）开始时的总桃子数：X = 5^n - 4
（2）老猴子最后能得到的桃子数：n + (X+4)*(4/5)^n - 4 = n + 4^n - 4
　　因为老猴子能得到的桃子主要有两个来源：一是每个小猴子都要给一个，有 n 只小猴子，就可以得到 n 个；二是最后剩余的桃子都归老猴子所有，从上面最后一次的结果来看，一共剩余了 (X+4)*(4/5)^n 个桃子，但是这里面包括我们最早借给它们的 4 个，实际上剩余的桃子数为 (X+4)*(4/5)^n - 4 ，所以最后总共能得到的桃子数就是 n + (X+4)*(4/5)^n - 4 。

import java.util.Scanner;  
public class Main { 
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        long n = 0;
        while(sc.hasNext()){
            n = sc.nextInt();
            if(n == 0)
                break;
            long a = (long)Math.pow(5, n); //5^n
            long b = (long)Math.pow(4, n);//4^n
            //a 最小需要桃子数 5^n-4 (X - 4)(减去借的4个桃子)
            //b 老猴子 分到的 n + (X+4)*(4/5)^n - 4 = n + 4^n - 4
            System.out.println((a-4)+" "+(b-4+n));
        }
    }
}

mkdir

mkdir

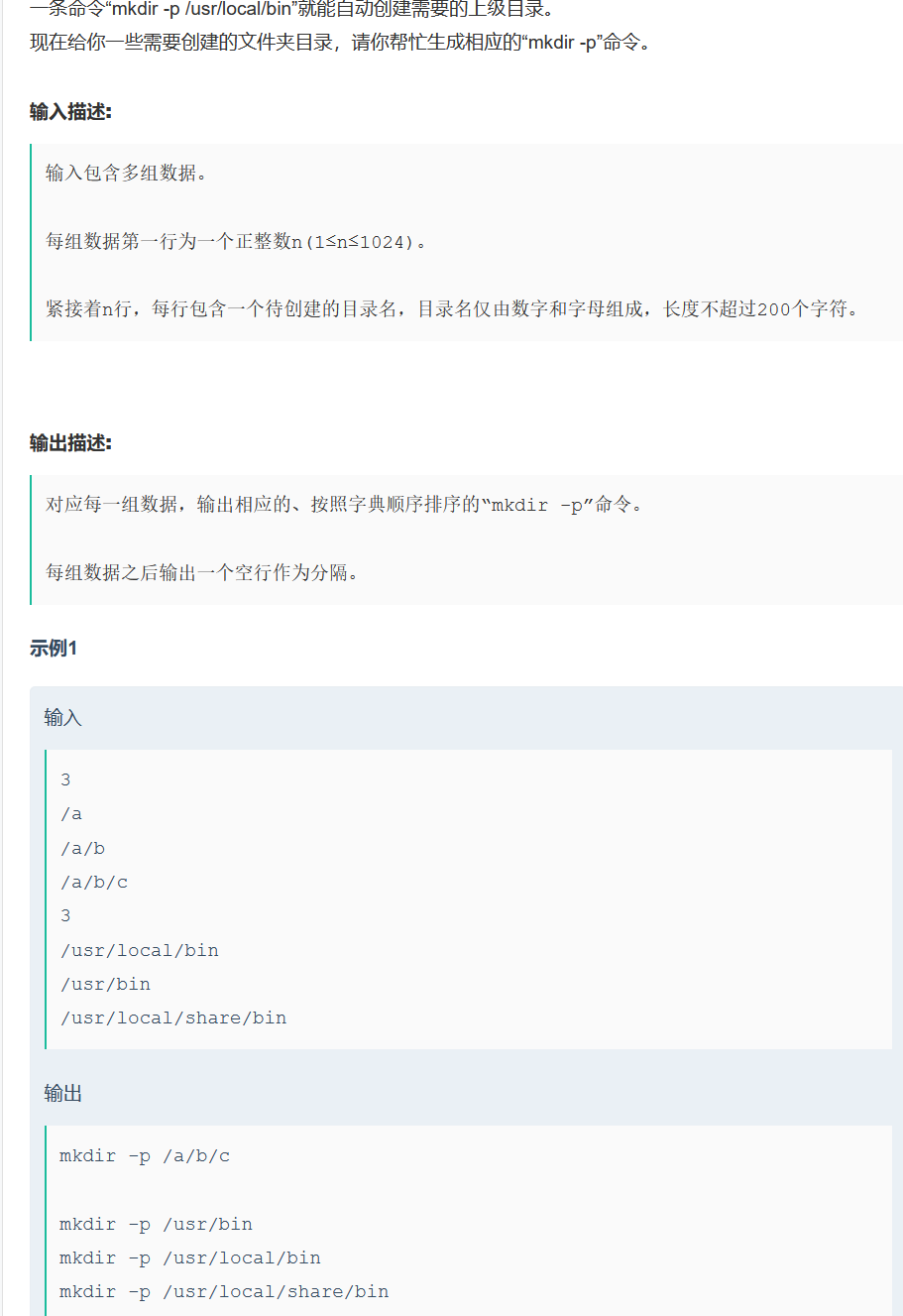
//方法一:
import java.util.*;
public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        while (sc.hasNext()) {
            int n = sc.nextInt();
            String[] arr = new String[n];
            for (int i = 0; i < arr.length; i ++ ) {
                arr[i] = sc.next();
            }
            Arrays.sort(arr);
            List<String> res = new ArrayList<>();
            for (int i = 1; i < arr.length; i ++ ) {
                if( ! arr[i].startsWith(arr[i - 1] + "/")) res.add(arr[i - 1]);
            }
            res.add(arr[n - 1]);
            for (String s:res) {
                System.out.println("mkdir -p " + s);
            }
            System.out.println();
        }
    }
}
//方法二:伪删除!
import java.util.*;
public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        while (sc.hasNext()) {
            int n = sc.nextInt();
            String[] arr = new String[n];
            for (int i = 0; i < arr.length; i ++ ) {
                arr[i] = sc.next();
            }
            Arrays.sort(arr);
            boolean[] flg = new boolean[n];
            //伪删除
           for(int i = 0;i<n-1;i++){
               if(arr[i].equals(arr[i+1])){
                   //相等保留一个!
                   flg[i] = true;
               }else if(arr[i].length()<arr[i+1].length()&&arr[i+1].contains(arr[i])&&arr[i+1].charAt(arr[i].length())=='/'){
                   flg[i] = true;
               }
           }
            for (int i=0;i<n;i++) {
                if(!flg[i])
                System.out.println("mkdir -p " + arr[i]);
            }
            System.out.println();
        }
    }
}