- 微信
- 微博
  
  分享文章到微博
- 复制链接
  
  复制链接到剪贴板

【模糊回归预测】基于matlab萤火虫算法优化模糊神经网络回归预测【含Matlab源码 2034期】

海神之光发表于 2022/08/15 00:39:07 2022/08/15

【摘要】一、萤火虫优化算法（FA）简介 1 介绍萤火虫（firefly）种类繁多，主要分布在热带地区。大多数萤火虫在短时间内产生有节奏的闪光。这种闪光是由于生物发光的一种化学反应，萤火虫的闪光模式因种类而异。...

一、萤火虫优化算法（FA）简介

1 介绍
萤火虫（firefly）种类繁多，主要分布在热带地区。大多数萤火虫在短时间内产生有节奏的闪光。这种闪光是由于生物发光的一种化学反应，萤火虫的闪光模式因种类而异。萤火虫算法(FA)是基于萤火虫的闪光行为，它是一种用于全局优化问题的智能随机算法，由Yang Xin-She（2009）[1]提出。萤火虫通过下腹的一种化学反应-生物发（bioluminescence）发光。这种生物发光是萤火虫求偶仪式的重要组成部分，也是雄性萤火虫和雌性萤火虫交流的主要媒介，发出光也可用来引诱配偶或猎物，同时这种闪光也有助于保护萤火虫的领地，并警告捕食者远离栖息地。在FA中，认为所有的萤火虫都是雌雄同体的，无论性别如何，它们都互相吸引。该算法的建立基于两个关键的概念：发出的光的强度和两个萤火虫之间产生的吸引力的程度。

2 天然萤火虫的行为
天然萤火虫在寻找猎物、吸引配偶和保护领地时表现出惊人的闪光行为，萤火虫大多生活在热带环境中。一般来说，它们产生冷光，如绿色、黄色或淡红色。萤火虫的吸引力取决于它的光照强度，对于任何一对萤火虫来说，较亮的萤火虫会吸引另一只萤火虫。所以，亮度较低的个体移向较亮的个体，同时光的亮度随着距离的增加而降低。萤火虫的闪光模式可能因物种而异，在一些萤火虫物种中，雌性会利用这种现象猎食其他物种；有些萤火虫在一大群萤火虫中表现出同步闪光的行为来吸引猎物，雌萤火虫从静止的位置观察雄萤火虫发出的闪光，在发现一个感兴趣趣的闪光后，雌性萤火虫会做出反应，发出闪光，求偶仪式就这样开始了。一些雌性萤火虫会产生其他种类萤火虫的闪光模式，来诱捕雄性萤火虫并吃掉它们。

3 萤火虫算法
萤火虫算法模拟了萤火虫的自然现象。真实的萤火虫自然地呈现出一种离散的闪烁模式，而萤火虫算法假设它们总是在发光。为了模拟萤火虫的这种闪烁行为，Yang Xin-She提出了了三条规则（Yang，2009）：
（1）假设所有萤火虫都是雌雄同体的，因此一只萤火虫可能会被其他任何萤火虫吸引。
（2）萤火虫的亮度决定其吸引力的大小，较亮的萤火虫吸引较暗的萤火虫。如果没有萤火虫比被考虑的萤火虫更亮，它就会随机移动。
（3）函数的最优值与萤火虫的亮度成正比。
光强(I)与光源距离（r）服从平方反比定律，因此由于空气的吸收，光的强度(I)随着与光源距离的增加而减小，这种现象将萤火虫的可见性限定在了非常有限的半径内：

萤火虫算法的主要实现步骤如下：

其中I0为距离r=0时的光强（最亮），即自身亮度，与目标函数值有关，目标值越优，亮度越亮；γ为吸收系数，因为荧光会随着距离的增加和传播媒介的吸收逐渐减弱，所以设置光强吸收系数以体现此特性，可设置为常数；r表示两个萤火虫之间的距离。有时也使用单调递减函数，如下式所示。

第二步为种群初始化：

其中t表示代数，xt表示个体的当前位置，β0exp(-γr2)是吸引度，αε是随机项。下一步将会计算萤火虫之间的吸引度：

其中β0表示r=0时的最大吸引度。
下一步，低亮度萤火虫向较亮萤火虫运动：

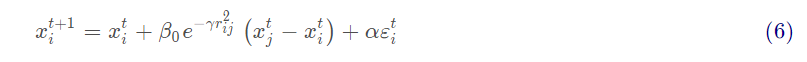
最后一个阶段，更新光照强度，并对所有萤火虫进行排序，以确定当前的最佳解决方案。萤火虫算法的主要步骤如下所示。

Begin
	初始化算法基本参数：设置萤火虫数目n，最大吸引度β0，光强吸收系数γ，步长因子α，最大迭代次数MaxGeneration或搜索精度ε；
	初始化：随机初始化萤火虫的位置，计算萤火虫的目标函数值作为各自最大荧光亮度I0；
	t=1
	while(t<=MaxGeneration || 精度>ε)
		计算群体中萤火虫的相对亮度I(式2)和吸引度β（式5），根据相对亮度决定萤火虫的移动方向；
		更新萤火虫的空间位置，对处在最佳位置的萤火虫进行随机移动（式6）；
		根据更新后萤火虫的位置，重新计算萤火虫的亮度I0；
		t=t+1
	end while
	输出全局极值点和最优个体值。
end


  
 
  1
  2
  3
  4
  5
  6
  7
  8
  9
  10
  11
  12
  13

萤火虫算法与粒子群算法(PSO)和细菌觅食算法(BFA)有相似之处。在位置更新方程中，FA和PSO都有两个主要分量：一个是确定性的，另一个是随机性的。在FA中，吸引力由两个组成部分决定：目标函数和距离，而在BFA中，细菌之间的吸引力也有两个组成部分：适应度和距离。萤火虫算法实现时，整个种群(如n)需要两个内循环，特定迭代需要一个外循环(如I)，因此最坏情况下FA的计算复杂度为O(n2I)。

二、部分源代码

clc;
clear;
warning(‘off’);
% Data Loading
data=JustLoad();
% Generate Fuzzy Model
ClusNum=4; % Number of Clusters in FCM
%
fis=GenerateFuzzy(data,ClusNum);
%
%% Tarining FireFly Algorithm
FireFlyFis=FireFlyRegression(fis,data);

%% Plot Fuzzy FireFly Results (Train - Test)
% Train Output Extraction
TrTar=data.TrainTargets;
TrainOutputs=evalfis(data.TrainInputs,FireFlyFis);
% Test Output Extraction
TsTar=data.TestTargets;
TestOutputs=evalfis(data.TestInputs,FireFlyFis);
% Train calc
Errors=data.TrainTargets-TrainOutputs;
MSE=mean(Errors.^2);RMSE=sqrt(MSE);
error_mean=mean(Errors);error_std=std(Errors);
% Test calc
Errors1=data.TestTargets-TestOutputs;
MSE1=mean(Errors1.^2);RMSE1=sqrt(MSE1);
error_mean1=mean(Errors1);error_std1=std(Errors1);
% Train
figure(‘units’,‘normalized’,‘outerposition’,[0 0 1 1])
subplot(3,2,1);
plot(data.TrainTargets,‘c’);hold on;
plot(TrainOutputs,‘k’);legend(‘Target’,‘Output’);
title(‘FireFly Training Part’);xlabel(‘Sample Index’);grid on;
% Test
subplot(3,2,2);
plot(data.TestTargets,‘c’);hold on;
plot(TestOutputs,‘k’);legend(‘FireFly Target’,‘FireFly Output’);
title(‘FireFly Testing Part’);xlabel(‘Sample Index’);grid on;
% Train
subplot(3,2,3);
plot(Errors,‘k’);legend(‘FireFly Training Error’);
title(['Train MSE = ’ num2str(MSE) ’ , Train RMSE = ’ num2str(RMSE)]);grid on;
% Test
subplot(3,2,4);
plot(Errors1,‘k’);legend(‘FireFly Testing Error’);
title(['Test MSE = ’ num2str(MSE1) ’ , Test RMSE = ’ num2str(RMSE1)]);grid on;
% Train
subplot(3,2,5);
h=histfit(Errors, 50);h(1).FaceColor = [.8 .8 0.3];
title(['Train Error Mean = ’ num2str(error_mean) ’ , Train Error STD = ’ num2str(error_std)]);
% Test
subplot(3,2,6);
h=histfit(Errors1, 50);h(1).FaceColor = [.8 .8 0.3];
title(['Test Error Mean = ’ num2str(error_mean1) ’ , Test Error STD = ’ num2str(error_std1)]);

%% Plot Just Fuzzy Results (Train - Test)
% Train Output Extraction
fTrainOutputs=evalfis(data.TrainInputs,fis);
% Test Output Extraction
fTestOutputs=evalfis(data.TestInputs,fis);
% Train calc
fErrors=data.TrainTargets-fTrainOutputs;
fMSE=mean(fErrors.^2);fRMSE=sqrt(fMSE);
ferror_mean=mean(fErrors);ferror_std=std(fErrors);
% Test calc
fErrors1=data.TestTargets-fTestOutputs;
fMSE1=mean(fErrors1.^2);fRMSE1=sqrt(fMSE1);
ferror_mean1=mean(fErrors1);ferror_std1=std(fErrors1);
% Train
figure(‘units’,‘normalized’,‘outerposition’,[0 0 1 1])
subplot(3,2,1);
plot(data.TrainTargets,‘m’);hold on;
plot(fTrainOutputs,‘k’);legend(‘Target’,‘Output’);
title(‘Fuzzy Training Part’);xlabel(‘Sample Index’);grid on;
% Test
subplot(3,2,2);
plot(data.TestTargets,‘m’);hold on;
plot(fTestOutputs,‘k’);legend(‘Target’,‘Output’);
title(‘Fuzzy Testing Part’);xlabel(‘Sample Index’);grid on;
% Train
subplot(3,2,3);
plot(fErrors,‘g’);legend(‘Fuzzy Training Error’);
title(['Train MSE = ’ num2str(fMSE) ’ , Test RMSE = ’ num2str(fRMSE)]);grid on;
% Test
subplot(3,2,4);
plot(fErrors1,‘g’);legend(‘Fuzzy Testing Error’);
title(['Train MSE = ’ num2str(fMSE1) ’ , Test RMSE = ’ num2str(fRMSE1)]);grid on;
% Train
subplot(3,2,5);
h=histfit(fErrors, 50);h(1).FaceColor = [.3 .8 0.3];
title(['Train Error Mean = ’ num2str(ferror_mean) ’ , Train Error STD = ’ num2str(ferror_std)]);
% Test
subplot(3,2,6);
h=histfit(fErrors1, 50);h(1).FaceColor = [.3 .8 0.3];
title(['Test Error Mean = ’ num2str(ferror_mean1) ’ , Test Error STD = ’ num2str(ferror_std1)]);

%% Regression Plots
figure(‘units’,‘normalized’,‘outerposition’,[0 0 1 1])
subplot(2,2,1)
[population2,gof] = fit(TrTar,TrainOutputs,‘poly4’);
plot(TrTar,TrainOutputs,‘o’,…
‘LineWidth’,1,…
‘MarkerSize’,6,…
‘MarkerEdgeColor’,‘g’,…
‘MarkerFaceColor’,[0.9,0.1,0.1]);
title(['FireFly Train - R = ’ num2str(1-gof.rmse)]);
xlabel(‘Train Target’);
ylabel(‘Train Output’);
hold on
plot(population2,‘b-’,‘predobs’);
xlabel(‘Train Target’);
ylabel(‘Train Output’);
hold off
subplot(2,2,2)
[population2,gof] = fit(TsTar, TestOutputs,‘poly4’);
plot(TsTar, TestOutputs,‘o’,…
‘LineWidth’,1,…
‘MarkerSize’,6,…
‘MarkerEdgeColor’,‘g’,…
‘MarkerFaceColor’,[0.9,0.1,0.1]);
title(['FireFly Test - R = ’ num2str(1-gof.rmse)]);
xlabel(‘Test Target’);
ylabel(‘Test Output’);
hold on
plot(population2,‘b-’,‘predobs’);
xlabel(‘Test Target’);
ylabel(‘Test Output’);
hold off
subplot(2,2,3)
[population2,gof] = fit(TrTar,fTrainOutputs,‘poly4’);
plot(TrTar,fTrainOutputs,‘o’,…
‘LineWidth’,1,…
‘MarkerSize’,6,…
‘MarkerEdgeColor’,‘b’,…
‘MarkerFaceColor’,[0.3,0.9,0.2]);
title(['Fuzzy Train - R = ’ num2str(1-gof.rmse)]);
xlabel(‘Train Target’);
ylabel(‘Train Output’);
hold on
plot(population2,‘r-’,‘predobs’);
xlabel(‘Train Target’);
ylabel(‘Train Output’);
hold off
subplot(2,2,4)
[population2,gof] = fit(TsTar, fTestOutputs,‘poly4’);
plot(TsTar, fTestOutputs,‘o’,…
‘LineWidth’,1,…
‘MarkerSize’,6,…
‘MarkerEdgeColor’,‘b’,…
‘MarkerFaceColor’,[0.3,0.9,0.2]);
title(['Fuzzy Test - R = ’ num2str(1-gof.rmse)]);
xlabel(‘Test Target’);
ylabel(‘Test Output’);
hold on
plot(population2,‘r-’,‘predobs’);
xlabel(‘Test Target’);
ylabel(‘Test Output’);
hold off
%% Errors
% Fuzzy Regression Train and Test Errors]
% Train
fprintf(‘Fuzzy Regression Training “MSE” Is = %0.4f.\n’,fMSE)
fprintf(‘Fuzzy Regression Training “RMSE” Is = %0.4f.\n’,fRMSE)
fprintf(‘Fuzzy Regression Training “Mean Error” Is = %0.4f.\n’,ferror_mean)
fprintf(‘Fuzzy Regression Training “STD Error” Is = %0.4f.\n’,ferror_std)
fprintf(‘Fuzzy Regression Training “MAE” Is = %0.4f.\n’,mae(data.TrainTargets,fTrainOutputs))
% Test
fprintf(‘Fuzzy Regression Testing “MSE” Is = %0.4f.\n’,fMSE1)
fprintf(‘Fuzzy Regression Testing “RMSE” Is = %0.4f.\n’,fRMSE1)
fprintf(‘Fuzzy Regression Testing “Mean Error” Is = %0.4f.\n’,ferror_mean1)
fprintf(‘Fuzzy Regression Testing “STD Error” Is = %0.4f.\n’,ferror_std1)
fprintf(‘Fuzzy Regression Testing “MAE” Is = %0.4f.\n’,mae(data.TestTargets,fTestOutputs))
% FireFly Regression Algorithm Train and Test Errors
% Train
fprintf(‘FireFly Regression Training “MSE” Is = %0.4f.\n’,MSE)
fprintf(‘FireFly Regression Training “RMSE” Is = %0.4f.\n’,RMSE)
fprintf(‘FireFly Regression Training “Mean Error” Is = %0.4f.\n’,error_mean)
fprintf(‘FireFly Regression Training “STD Error” Is = %0.4f.\n’,error_std)
fprintf(‘FireFly Regression Training “MAE” Is = %0.4f.\n’,mae(data.TrainTargets,TrainOutputs))
% Test
fprintf(‘FireFly Regression Testing “MSE” Is = %0.4f.\n’,MSE1)
fprintf(‘FireFly Regression Testing “RMSE” Is = %0.4f.\n’,RMSE1)
fprintf(‘FireFly Regression Testing “Mean Error” Is = %0.4f.\n’,error_mean1)
fprintf(‘FireFly Regression Testing “STD Error” Is = %0.4f.\n’,error_std1)
fprintf(‘FireFly Regression Testing “MAE” Is = %0.4f.\n’,mae(data.TestTargets,TestOutputs))


## 三、运行结果
![在这里插入图片描述](https://img-blog.csdnimg.cn/275d291165fb4e0a9769d1bc2fb70796.jpeg#pic_center)
![在这里插入图片描述](https://img-blog.csdnimg.cn/ffb8a2710e75485b89845b3ffe9b86e9.png#pic_center)
![在这里插入图片描述](https://img-blog.csdnimg.cn/e087f7517b3a4a948e9fbae59017225c.png#pic_center)
![在这里插入图片描述](https://img-blog.csdnimg.cn/a9750c6003674066977c2203346f26d2.png#pic_center)

## 四、matlab版本及参考文献
**1 matlab版本**
2014a

**2 参考文献**
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例（第2版）[M].电子工业出版社，2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社，2017.
[3][群体智能优化算法之萤火虫算法(Firefly Algorithm，FA)](https://blog.csdn.net/hba646333407/article/details/103080856?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522162937179216780264099934%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=162937179216780264099934&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~sobaiduend~default-3-103080856.first_rank_v2_pc_rank_v29&utm_term=%E8%90%A4%E7%81%AB%E8%99%AB%E4%BC%98%E5%8C%96%E7%AE%97%E6%B3%95&spm=1018.2226.3001.4187)
 
**3 备注**
简介此部分摘自互联网，仅供参考，若侵权，联系删除
 



  
 
  
 
 
  1
  2
  3
  4
  5
  6
  7
  8
  9
  10
  11
  12
  13
  14
  15
  16
  17
  18
  19
  20
  21

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/126323947

点赞
收藏
关注作者

0/1000

抱歉，系统识别当前为高风险访问，暂不支持该操作

全部回复

上滑加载中

设置昵称

在此一键设置昵称，即可参与社区互动！

*长度不超过10个汉字或20个英文字符，设置后3个月内不可修改。

确认取消

加入云驻计划，成为创作者

华为云周边好礼
免费体验产品
特殊身份标识
线下官方门票
内部专家零距离
与10000+优质创作者共同成长

立即加入

【模糊回归预测】基于matlab萤火虫算法优化模糊神经网络回归预测【含Matlab源码 2034期】

一、萤火虫优化算法（FA）简介

二、部分源代码

全部回复

设置昵称

关于作者

目录

加入云驻计划，成为创作者

【模糊回归预测】基于matlab萤火虫算法优化模糊神经网络回归预测【含Matlab源码 2034期】

一、萤火虫优化算法（FA）简介

二、部分源代码

全部回复

设置昵称

关于作者

目录

加入云驻计划，成为创作者

推荐阅读

相关产品