前言

Swin Transformer是2021年微软研究院发表在ICCV上的一篇文章，问世时在图像分类、目标检测、语义分割多个领域都屠榜。

根据论文摘要所述，Swin Transformer在图像分类数据集ImageNet-1K上取得了87.3%的准确率，在目标检测数据集COCO上取得了58.7%的box AP和51.1%的mask AP，在语义分割数据集ADE20K上去的了53.5%的mIoU。

论文名称：Swin Transformer: Hierarchical Vision Transformer using Shifted Windows
原论文地址： https://arxiv.org/abs/2103.14030
开源代码地址：https://github.com/microsoft/Swin-Transformer

思想概述

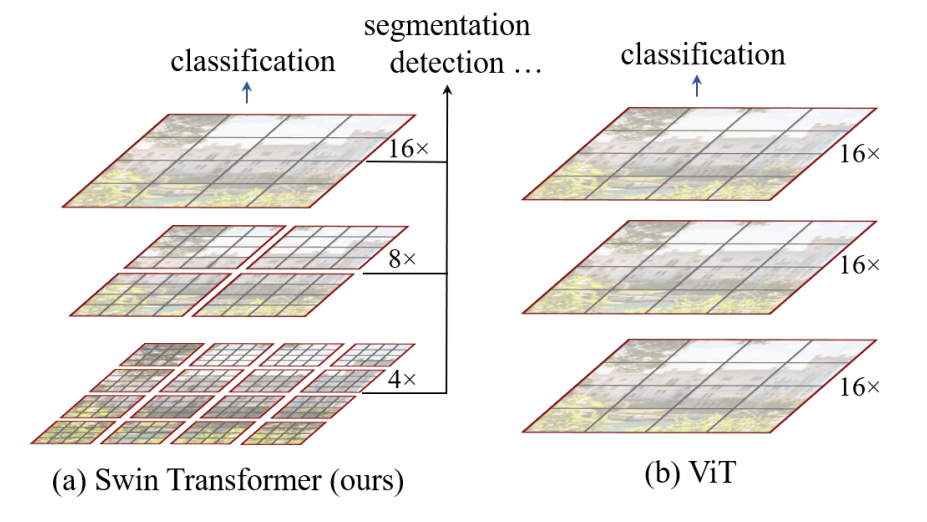
Swin Transformer的思想比较容易理解，如下图所示，ViT(Vision Transformer)的思想是将图片分成16x16大小的patch，每个patch进行注意力机制的计算。而Swin Transformer并不是将所有的图片分成16x16大小的patch，有16x16的，有8x8的，有4x4的。每一个patch作为一个单独的窗口，每一个窗口不再和其它窗口直接计算注意力，而是在自己内部计算注意力，这样就大幅减小了计算量。

为了弥补不同窗口之间的信息传递，Swin Transformer又提出了移动窗口(Shifted Window)的概念(Swin)，后续详细进行分析。

分块详解

整体架构

Swin Transformer有多种变体，论文中给出的这幅图是Swin-T的模型架构图。

下面就按照图片输入到输出的顺序，对各模块进行分析。

Patch Partion

输入图片尺寸为HxWx3，Patch Partion作用就是将图片进行分块。对于每一个Patch，尺寸设定为4x4。然后将所有的Patch在第三维度(颜色通道）上进行叠加，那么经过Patch Partion之后，图片的维度就变成了[H/4,W/4,4x4x3]=[H/4,W/4,48]

Linear Embeding

Linear Embeding作用是对通道数进行线性变换，经过Linear Embeding之后，图片维度从[H/4, W/4, 48]变成了 [H/4, W/4, C]。

Swin Transformer Block

Swin Transformer Block是Swin Transformer的核心部分，首先明确Swin Transformer Block的输入输出图片维度是不发生变化的。图中的x2表示，Swin Transformer Block有两个结构，在右侧小图中，这两个结构仅有W-MSA和SW-MSA的差别，这两个结构是成对使用的，即先经过左边的带有W-MSA的结构再经过右边带有SW-MSA的结构。

W-MSA

W-MSA模块就是将特征图划分到一个个窗口(Windows)中，在每个窗口内分别使用多头注意力模块。
论文在这里还强调了一下W-MSA和MSA计算量的对比，计算公式如下：

MSA就是之前ViT不加窗口计算全局注意力。下面就来看看这两个式子是如何计算得到的。
先看MSA：在Transformer中，注意力的计算公式如下所示：

在ViT中，输入矩阵A的维度为[hw,C]，Q的维度也是[hw,C]，那么相乘的权重矩阵维度W1的维度是[C,C]。Q=AxW1，这样的的计算量就是$hw{C}^2$，同时K和V的计算同理，这样就已经有$3hw{C}^2$。

之后，Q和K的转置相乘，即[hw,C]x[C,hw]，这样的计算量为$(hw{)}^{2}C$，同理再乘上V，那样就已经有$3hw{C}^2+2(hw{)}^{2}C$计算量。

最后，考虑到多头注意力机制，所有的计算头最终还需要和一个融合矩阵相乘，又多一个$hw{C}^2$，这样MSA总的计算量就为$4hw{C}^2+2(hw{)}^{2}C$

下面再看W-MSA：这里的M指的是一个窗口的长宽，即一个窗口尺寸为MxM，那么对于一个窗口而言，完全可以带入上面MSA的公式，即一个窗口的计算量为$4M^2{C}^2+2M^{4}C$，窗口总数为$\frac{h}{M}\times \frac{w}{M}$。
因此W-MSA总的计算量就为$\frac{h}{M}\times \frac{w}{M}\times (4M^2{C}^2+2M^{4}C)=4hw{C}^2+2M^{2}hwC$

如果h和w很大，而M比较小，那么这样操作将大大减少计算量。

SW-MSA

第一个Swin Transformer Block的MLP结构和之前ViT一样，没有新东西，下面就到第二个Swin Transformer Block中的SW-MSA模块。

SW-MSA主要是为了让窗口与窗口之间可以发生信息传输。
论文中给出了这样一幅图来描述SW-MSA。

值得注意的是，表面上看从4个窗口变成了9个窗口，实际上是整个窗口网格从左上角分别向右侧和下方各偏移了M/2个像素。但是这样又产生了一个新的问题，那就是每个窗口大小不一样，不利于计算。

于是作者又想到了一个“天才级”的想法，即将左上角的窗口移动到右下角进行合并。

这样就可以计算在新生成的四个窗口中计算内部注意力，但是仍然存在的一个问题是原本的不同模块是从上面移下来的，不应该和原本的下方模块计算注意力，比如天空和大地计算注意力会出问题。于是作者又添加了一个掩码矩阵。对于每一个窗口分别设计一个掩码矩阵，其中对于不应该被计算的部分，掩码矩阵就赋值为-100，这样后续通过Softmax计算之后，最终就变成0，相当于起到过滤作用。

Patch Merging

第一个Stage结束之后，后面3个Stage的结构完全一样。和第一个Stage不同的是，后面几个Stage均多了一个Patch Merging的操作。
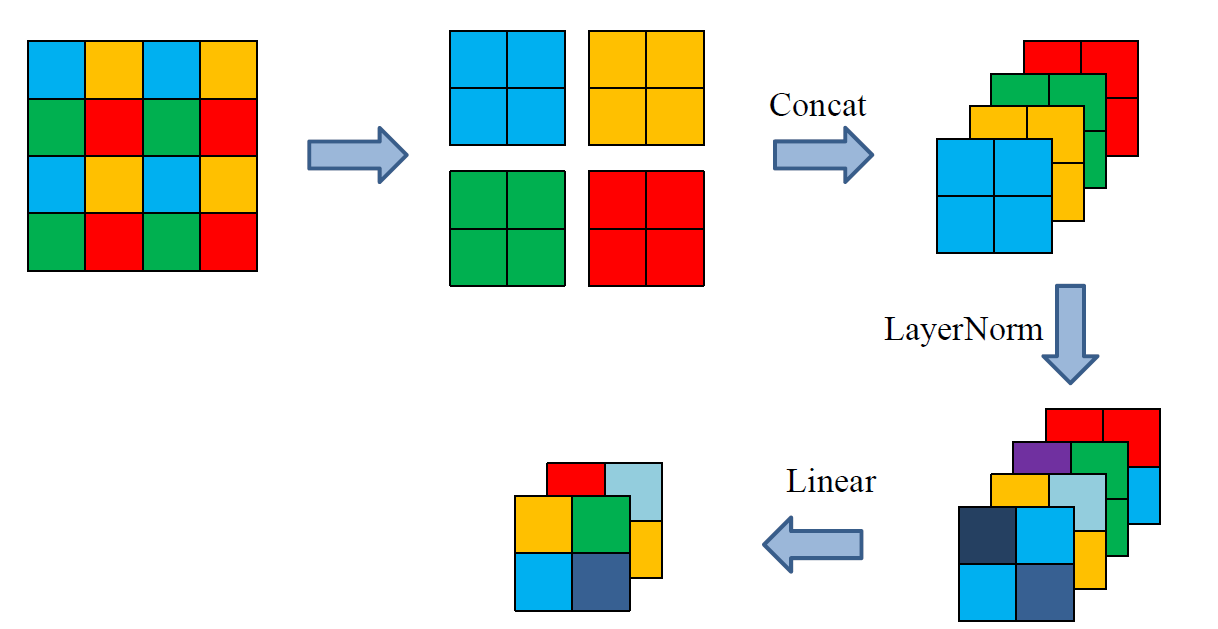
Patch Merging的操作不难理解，首先是将一个矩阵按间隔提取出四个小矩阵，然后将这四个矩阵在第三通道上进行Concat，在进行LayerNorm之后，通过一个线性层映射成2个通道。这样，通过Patch Merging操作之后的特征图长宽分别减半，通道数翻倍。

下图比较清晰地展示了 Patch Merging的操作过程，图源[1]。

相对位置偏置(Relative Position Bias)

上面已经按照流程将Swin Transformer的核心内容整理清楚了，在论文的最后部分，作者还提出了一种相对位置偏置的计算方法。

使用该方法之后，可以看到结果会有小幅提升：

不过，作者没有细讲该方法的具体原理，看到这篇文章解读得不错，直接放在这里。

对比测试结果

最后，作者在不同领域，和其它算法进行了对比测试，可以看到，Swin-L基本均取得了最好效果。

不同版本

Swin Transformer根据不同的配置参数大小，主要可以分下面四个版本。

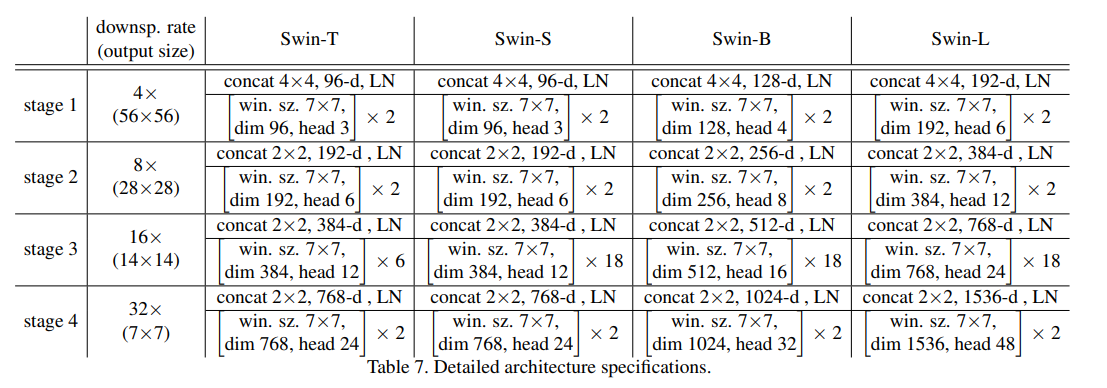
表中：

• win. sz. 7x7表示使用的窗口（Windows）的大小
• dim表示feature map的channel深度（或者说token的向量长度）
• head表示多头注意力模块中head的个数

实践测试

实践测试我找的是和之前ViT类似的图像分类例子，使用的花卉数据集。
代码仓库地址：https://github.com/WZMIAOMIAO/deep-learning-for-image-processing/tree/master/pytorch_classification/swin_transformer

我用Swin-S这个模型进行训练，相比于之前的ViT，模型训练速度几乎提升了一倍，最终精度也比ViT略高一些。

代码备份

下面是我跑的代码备份，里面包括了我所下载的预训练模型。（模型大小也几乎是ViT的一半)
https://pan.baidu.com/s/1B9SAXZ7AWPlwpZZ_T6gUKQ?pwd=8888

References

[1]https://blog.csdn.net/qq_37541097/article/details/121119988
[2]https://www.bilibili.com/video/BV13L4y1475U

文章来源: zstar.blog.csdn.net，作者：zstar-_，版权归原作者所有，如需转载，请联系作者。

原文链接：zstar.blog.csdn.net/article/details/126269534