【BP数据预测】基于matlab灰狼算法优化BP神经网络数据预测（多输入多输出）【含Matlab源码 2026期】

一、灰狼算法及BP神经网络简介

1 BP算法
BP (Back—Propagation) 神经网络是由Rumelhart, McClelland提出的概念, 其结构简单、可操作性强, 具有非线性映射能力, 是目前应用最广泛的人工神经网络。但BP算法存在收敛速度慢、容易陷入局部最优等缺陷, 在很大程度上影响了预测结果。BP模型如图1所示, 该模型包括输入层、隐层、输出层, 其中W、V为连接权矩阵, 跨层的神经元之间则不连接。

图1 BP神经网络结构图
BP神经网络算法由信号的正向传播和误差的反向传播两个过程组成。正向传播, 输入信号通过隐含层处理, 经过非线性变换, 转向输出层产生输出信号, 若输出值与期望值不符, 则转入反向传播过程。误差反传是将输出误差信号通过隐含层向输入层逐层反传, 通过修改各神经元的权值, 使误差沿梯度方向下降, 这样反复学习训练, 直到输出的误差达到要求或者达到最大迭代次数, 训练停止。
（1）权值初始化
将网络中的所有权值随机初始化。
（2） 根据实例的输入, 计算输出层每个单元的输出。
网络的实际输出及隐层单元的状态Okj, 由公式 (1) 计算:

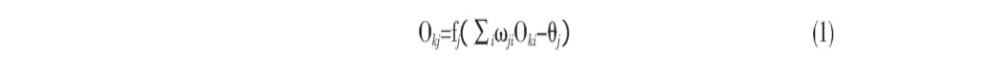
公式中, θj是阈值, 一般可采用Sigmoid函数, 即公式 (2) 作为激励函数作用于它。

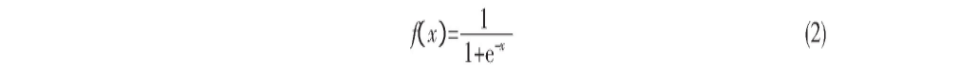
（3） 计算网络各层误差信号
对于输出层的每个单元k, 误差δk, 由公式 (3) 计算:

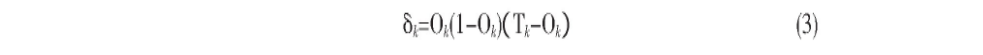
Ok是单元k的实际输出值, Ok (1-Ok) 是Logistic函数的导数, 而Tk是基于k给定训练元组的已知目标值。
而对于隐藏层单元h的误差由公式 (4) 计算:

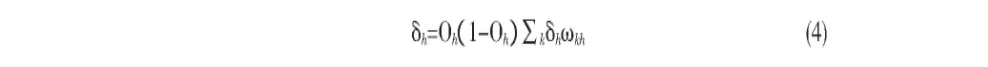
（4）调整各层的权值
公式 (5) 是权值的更新公式, 公式 (6) 阈值的更新公式。

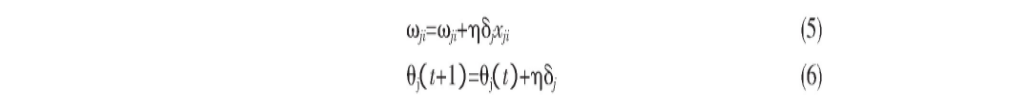
（5）核查算法是否符合结束条件
如果网络总误差满足设定的精度要求或符合结束条件, 训练过程结束。否则, 继续进行下一轮训练。

2 GWO算法
GWO算法是Mirjalil等人2014年提出的一种新型群智能优化算法, 该算法通过模拟自然界中灰狼的狩猎跟踪、追捕、包围和攻击等建立一个数学模型, 进而完成最优化工作。整个狼群按照适应度值被分为最优灰狼α、次优灰狼β、第三优灰狼β和其他狼ω四个等级。在捕食过程中α、β、δ灰狼追捕猎物, ω狼追随前三者进向着目标搜索。捕食过程中, 灰狼个体与猎物的距离为:

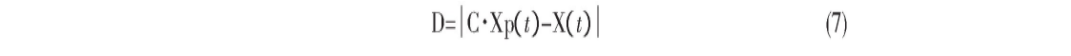
公式中t表示迭代次数;Xp (t) 是猎物的位置, X (t) 表示第t代时灰狼的位置, D表示猎物与灰狼之间的距离, C=2r1。
灰狼位置更新为:

其中, a是收敛因子, 取值[0, 2], max是最大迭代次数;r2和r2均是[0, 1]的随机数:当|A|>1时, 灰狼群体将搜索范围扩大, 进行全局搜索;|A|<1时, 灰狼群体将包围圈缩小, 进行局部搜索。

在狼群中, 利用α、β、δ这三头狼的位置跟踪猎物的数学描述如下:

式 (12) 和式 (13) 定义了狼群内ω与α、β、δ的距离关系。

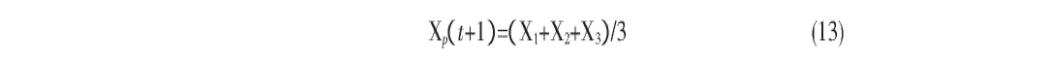
式 (13) 根据α、β、δ的位置计算ω狼的最终位置。

3 GWO优化BP神经网络
由于BP神经网络采用均方误差梯度下降方向进行收敛, 因此容易陷入局部最优, 且收敛速度慢, 而且BP神经网络对初始化参数中的权值和阀值具有较大的敏感性。本文采用GWO优化BP神经网络, 以达到克服BP算法的缺陷, 避免陷入局部最优, 而且使收敛加速。
用GWO优化BP神经网络, 即将灰狼的位置信息作为BP神经网络的权重和阈值, 灰狼不断对猎物的位置进行判断和更新, 相当于在不断更新BP神经网络的阈值和权重, 通过多次迭代, 最终计算全局最优结果。优化BP神经网络具体步骤:
1.初始化参数。包括灰狼种群大小、灰狼个体位置信息的维度、灰狼维度的上界和下界, 最大迭代次数、随机初始化灰狼位置。
2.将灰狼的位置映射给BP神经网络, 按照公式计算适应度
3.适应度值的计算:狼群内部按照等级被分为最优、次优、第三优、和普通狼四组, 并根据与的位置, 用公式 (11) ～ (13) 更新的位置信息, 并更新参数a、A和C的值。
4.判断灰狼个体的每一维度越界情况, 如有越界, 把灰狼维度的上界或下界设置为越界的值。
5.判断迭代次数:如果小于最大迭代次数, 重复步骤2-步骤5, 继续下一次迭代, 直到满足条件;否则结束算法。

二、部分源代码

clear
clc
tic
global SamIn SamOut HiddenUnitNum InDim OutDim TrainSamNum
%% 导入训练数据
data = xlsread(‘test_data1.xlsx’);
[data_m,data_n] = size(data);%获取数据维度

P = 80; %百分之P的数据用于训练，其余测试
Ind = floor(P * data_m / 100);

train_data = data(1:Ind,1:end-1)‘;
train_result = data(1:Ind,end)’;
test_data = data(Ind+1:end,1:end-1)‘;% 利用训练好的网络进行预测
test_result = data(Ind+1:end,end)’;

%% 初始化参数
[InDim,TrainSamNum] = size(train_data);% 学习样本数量
[OutDim,TrainSamNum] = size(train_result);
HiddenUnitNum = 7; % 隐含层神经元个数

[SamIn,PS_i] = mapminmax(train_data,0,1); % 原始样本对（输入和输出）初始化
[SamOut,PS_o] = mapminmax(train_result,0,1);

W1 = HiddenUnitNumInDim; % 初始化输入层与隐含层之间的权值
B1 = HiddenUnitNum; % 初始化输入层与隐含层之间的阈值
W2 = OutDimHiddenUnitNum; % 初始化输出层与隐含层之间的权值
B2 = OutDim; % 初始化输出层与隐含层之间的阈值
L = W1+B1+W2+B2; %粒子维度
%%优化参数的设定
dim=L; % 优化的参数 number of your variables
for j=1:L
lb(1,j)=-3.5; % 参数取值下界
ub(1,j)=3.5;
end% 参数取值上界

%%GWO算法初始化
SearchAgents_no=150; % 狼群数量，Number of search agents
Max_iteration=3000; % 最大迭代次数，Maximum numbef of iterations

% initialize alpha, beta, and delta_posAlpha_pos=zeros(1,dim); % 初始化Alpha狼的位置
Alpha_score=inf; % 初始化Alpha狼的目标函数值，change this to -inf for maximization problems

Beta_pos=zeros(1,dim); % 初始化Beta狼的位置
Beta_score=inf; % 初始化Beta狼的目标函数值，change this to -inf for maximization problems

Delta_pos=zeros(1,dim); % 初始化Delta狼的位置
Delta_score=inf; % 初始化Delta狼的目标函数值，change this to -inf for maximization problems

%Initialize the positions of search agents
Positions=initialization(SearchAgents_no,dim,ub,lb);

Convergence_curve=zeros(1,Max_iteration);

l=0; % Loop counter循环计数器

% Main loop主循环
while l<Max_iteration % 对迭代次数循环

for i=1:size(Positions,1)  % 遍历每个狼


  
    % Update Alpha, Beta, and Delta
    if fitness<Alpha_score % 如果目标函数值小于Alpha狼的目标函数值
        Alpha_score=fitness; % 则将Alpha狼的目标函数值更新为最优目标函数值，Update alpha
        Alpha_pos=Positions(i,:); % 同时将Alpha狼的位置更新为最优位置
    end

    if fitness>Alpha_score && fitness<Beta_score % 如果目标函数值介于于Alpha狼和Beta狼的目标函数值之间
        Beta_score=fitness; % 则将Beta狼的目标函数值更新为最优目标函数值，Update beta
        Beta_pos=Positions(i,:); % 同时更新Beta狼的位置
    end

    if fitness>Alpha_score && fitness>Beta_score && fitness<Delta_score  % 如果目标函数值介于于Beta狼和Delta狼的目标函数值之间
        Delta_score=fitness; % 则将Delta狼的目标函数值更新为最优目标函数值，Update delta
        Delta_pos=Positions(i,:); % 同时更新Delta狼的位置
    end
end

a=2-l*((2)/Max_iteration); % 对每一次迭代，计算相应的a值，a decreases linearly fron 2 to 0

% Update the Position of search agents including omegas
for i=1:size(Positions,1) % 遍历每个狼
    for j=1:size(Positions,2) % 遍历每个维度

        

        % Alpha狼位置更新
        D_alpha=abs(C1*Alpha_pos(j)-Positions(i,j)); % Equation (3.5)-part 1
        X1=Alpha_pos(j)-A1*D_alpha; % Equation (3.6)-part 1

        r1=rand();
        r2=rand();

        A2=2*a*r1-a; % 计算系数A，Equation (3.3)
        C2=2*r2; % 计算系数C，Equation (3.4)

        % Beta狼位置更新


        A3=2*a*r1-a; % 计算系数A，Equation (3.3)
        C3=2*r2; % 计算系数C，Equation (3.4)

        % Delta狼位置更新
        D_delta=abs(C3*Delta_pos(j)-Positions(i,j)); % Equation (3.5)-part 3
        X3=Delta_pos(j)-A3*D_delta; % Equation (3.5)-part 3 
        
        % 位置更新
        Positions(i,j)=(X1+X2+X3)/3;% Equation (3.7)
        

    end
end

l=l+1
Convergence_curve(l)=Alpha_score;

  

 

  
 
 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
  
33
  
34
  
35
  
36
  
37
  
38
  
39
  
40
  
41
  
42
  
43
  
44
  
45
  
46
  
47
  
48
  
49
  
50
  
51
  
52
  
53
  
54
  
55
  
56
  
57
  
58
 

end
x=Alpha_pos;
%%
% x = gb;
W1 = x(1:HiddenUnitNumInDim);
L1 = length(W1);
W1 = reshape(W1,[HiddenUnitNum, InDim]);
B1 = x(L1+1:L1+HiddenUnitNum)';
L2 = L1 + length(B1);
W2 = x(L2+1:L2+OutDimHiddenUnitNum);
L3 = L2 + length(W2);
W2 = reshape(W2,[OutDim, HiddenUnitNum]);
B2 = x(L3+1:L3+OutDim)';
HiddenOut = logsig(W1 * SamIn + repmat(B1, 1, TrainSamNum)); % 隐含层网络输出
NetworkOut = W2 * HiddenOut + repmat(B2, 1, TrainSamNum); % 输出层网络输出
Error = SamOut - NetworkOut; % 实际输出与网络输出之差

SamIn_test= mapminmax(‘apply’,test_data,PS_i); % 原始样本对（输入和输出）初始化
HiddenOut_test = logsig(W1 * SamIn_test + repmat(B1, 1, ForcastSamNum)); % 隐含层输出预测结果
NetworkOut = W2 * HiddenOut_test + repmat(B2, 1, ForcastSamNum); % 输出层输出预测结果
Forcast_data_test = mapminmax(‘reverse’,NetworkOut,PS_o);
test_error=test_result(1,:)-Forcast_data_test(1,:);
mean_error=mean(abs(test_error)/test_result)
% test_mse=mean(test_error.^2)
test_mse=sqrt(mean(test_error.^2))
%% 绘制结果
figure
plot(Convergence_curve,‘r’)
xlabel(‘迭代次数’)
ylabel(‘适应度’)
title(‘收敛曲线’)
figure
subplot(2,2,1);
plot(train_result(1,:), ‘r-')
hold on
plot(Forcast_data(1,:), ‘b-o’);
legend(‘真实值’,‘拟合值’)
title(‘输出训练集拟合效果’)
subplot(2,2,2);
plot(test_result(1,:), 'r-’)
hold on
plot(Forcast_data_test(1,:), ‘b-o’);
legend(‘真实值’,‘预测值’)
title(‘输出测试集预测效果’)
subplot(2,2,3);
stem(train_result(1,:) - Forcast_data(1,:))
title(‘输出训练集误差’)
subplot(2,2,4);
stem(test_result(1,:) - Forcast_data_test(1,:))
title(‘输出测试集误差’)
toc
%save(‘灰狼算法预测2-4’)

三、运行结果

四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1]于淑香,温一军.基于GWO-BP算法的软件缺陷预测模型[J].安徽电子信息职业技术学院学报. 2018,17(06)

3 备注
简介此部分摘自互联网，仅供参考，若侵权，联系删除

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/126273039