数据结构杂谈(六)——队列
本文的所有代码均由C++编写
六 队列
6.1 队列的定义
与栈相反,队列(Queue)是一种先进先出(Fisrt in first out,FIFO)的结构。在此,我们先给出队列的定义:
队列是只允许在一端进行插入操作,而在另一端进行删除操作的线性表
举一个生活中的例子,如下图所示:

对的,你没看错,队列实际上就这么简单,我们把往队列中添加结点叫做入队,往队列中删除结点叫做出队。入队的一端叫队尾,出队的一端叫队头,这都是可以和生活中联系起来的。
我们把上面的图抽象一下,变成下面的形式:
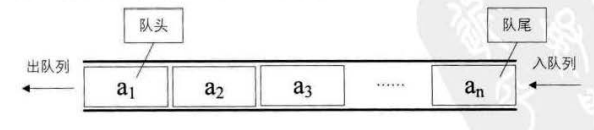
队列在程序设计中应用地非常频繁,比如键盘输入字母到记事本上,你依次输入god,总不能记事本上面写的是dog吧。
学过操作系统的朋友也了解就绪队列这个名词,在进程调度中,队列也经常出现,在时间片调度算法中,一个进程从队头上处理器运行的时候,当时间片轮换时,这个进程若未执行完成,将会回到该就绪队列的队尾。
6.2 队列的抽象数据类型
同样,队列也可以用线性表来表示,当然也就分为了顺序队列和链式队列了。在探讨这些之前,我们先了解一下队列的抽象数据类型:
ADT 队列(Queue)
Data
同线性表。元素具有相同的类型,相邻元素具有前驱和后继关系。
Operation
InitQueue(*Q):初始化操作,建立一个空队列Q。
DestroyQueue(*Q):若队列Q存在,则销毁它。
ClearQueue(*Q):将队列Q清空。
QueueEmpty(Q):若队列Q为空,返回true,否咋返回false。
Gethead(Q,*e):若队列Q存在且非空,用e返回队列Q的队头元素。
EnQueue(*Q,e):若队列Q存在,插入新元素e到队列Q中并成为队尾元素。
DeQueue(*Q,e):删除队列Q中队头元素,并用e返回其值。
QueueLength(Q):返回队列Q的元素个数。
endADT
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
6.3 顺序队列(循环队列)
6.3.1 顺序队列的定义及初始化
对于队列的定义,同样无需多讲,上代码。
//静态数组大小
#define MaxSize 10
//顺序队列定义
typedef int QElemType;
typedef struct SqQueue
{
QElemType data[MaxSize];//静态数组存放队列元素
int front, rear;//队头和队尾指针
}SqQueue;
//初始化
void InitQueue(SqQueue& Q)
{
Q.front = 0;
Q.rear = 0;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
如果需要判断队列是否为空,只需判断队头指针是否等于队尾指针即可。
//判空
bool QueueEmpty(SqQueue Q)
{
if (Q.rear == Q.front)
return true;
else
return false;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
6.3.2 入队
对于入队,我们需要注意一个事情。
假设我们用一个静态数组来存放队列,那么队头指针指向队头元素,队尾指针指向队尾元素。当添加队列元素时,队尾指针+1,而当删除队列元素时,队头指针+1,也就是说,当队尾指针等于静态数组最大容量的时候,只能说明添加队列的元素刚好处于数组最后,而不能说明队列容量不足。这个情况在《大话数据结构》中叫做假溢出。
换而言之,队头元素不一定在数组的0号索引,队尾数组不一定在数组的MaxSize号索引。
这样的做法有别于我们前面讲到的顺序表的插入,在顺序表中,我们插入是当插入一个元素,所有往后的元素都要移动一位,但是这样就会造成时间复杂度过大,其花的时间都在移动元素上。为了解决时间问题,我们才抛出上述的做法。
那我们如何来处理顺序队列判断是否溢出呢?
这个问题的抛出,引出了顺序队列的本名:循环队列。我们在此给出循环队列的定义:
我们把队列中头尾相接的顺序存储结构称为循环队列。
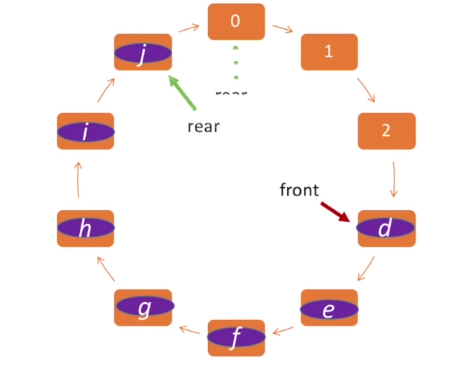
我们来尝试处理这个问题,采用的方法有两种。什么意思呢?我们发现当新元素入队时,队尾指针跟着新元素,如上图所示,我们最开始初始化是让front指针和rear指针重合,所以再次重合时就是队列溢出的时候,由此我们可以引出第一个方法:
设置一个标志flag,最开始初始化时,front == rear,此时flag = 0,表示队列为空,第二次front == rear,此时flag = 1,表示队列溢出。
我们还可以有一种方法,即牺牲一个位置。当队列满的时候,数组中还有一个空闲单元。

由此我们可以引入第二个方法:
在判别满的情况时我们的条件是(rear+1)% == front。
rear和front在数组中的位置那个在0号位那个在MaxSize号位是可以自己指定的,考虑到循环的问题,它们相遇有可能是在同一圈,也有可能相差了一圈后相遇,所以我们的判别溢出条件应该为(rear+1)%MaxSize = front。
上面可能有点乱,我们来看看下面的例子:
在上图的左边front处于0号位,rear处于4号位,按照上面我们说的,(4+1)%5 = 0,说明队列已满;如上图所示右边front处于2号位,rear处于1号位,如上所说(1+1)%5 = 2,说明队列已满。
取余运算是除法中的术语,取余数是指整数除法中被除数未被除尽部分,如7%2 = 1。这是大的数取余一个小的数;而当一个小的数取余一个大的数时,商为0,所以余数为自己,如2%5 = 2。
让我们回到本小节的主题,入队。既然弄清楚原理,代码也好写了。
//入队
bool EnQueue(SqQueue& Q, QElemType x)
{
if ((Q.rear + 1) %MaxSize == Q.front)
{
return false;
}
//新元素插入队尾
Q.data[Q.rear] = x;
//移动队尾指针
Q.rear = (Q.rear + 1) % MaxSize;
return true;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
6.3.3 出队
当然的,如果是要删除队列中的元素,即把队头元素删除,当然需要注意的是注意判空。
//出队
bool DeQueue(SqQueue& Q, QElemType& x)
{
//判断队列是否为空
if (Q.rear == Q.front)
{
return false;//队列为空无法删除
}
x = Q.data[Q.front];
Q.front = (Q.front + 1) % MaxSize;
return true;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
6.3.4 获取队头元素
//获取队头元素
bool GetHead(SqQueue Q, QElemType& x)
{
if (Q.rear == Q.front)
return false;//队空则报错
x = Q.data[Q.front];
return true;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
6.3.5 获取队列长度
//获取队列长度
bool QueueLength(SqQueue Q,QElemType &x)
{
x = (Q.rear + MaxSize - Q.front) % MaxSize;
return true;
}
- 1
- 2
- 3
- 4
- 5
- 6
6.3.6 回过头来
上面讲述了两种方法来判断是否溢出,我们在链栈中还采用了统计表长的方式来判断栈栈,那么在队列中我们同样可以这么做,用一个整形的length来记录队列长度,当队列长度大于MaxSize时,即队列溢出,所以我们可以用条件if(length == MaxSize)来作为判断条件。
根据初始化的不同,实际上对应的代码都会有所不同,采用什么方法去判断满队列就会有三种不同写法,而在空队列时,初始化两个指针指向何处也会导致代码的不同。在本笔记中,我们采用的是队头和队尾指向同一个位置,当添加一个元素时,队尾指针会移向队尾元素的下一位;而在某些题目或教材中,队尾指针可能是指向队尾元素的。
在考研中,以上三种方法均有可能出现,望周知。
6.4 链式队列
队列的链式存储结构,其实就是线性表的单链表,只不过它只能尾进头出罢了。我们把它简称为链队列。
对于链队列来说,用带头结点的方式去实现就会更好一些。其中队头指针指向头结点,队尾指针指向队尾元素,以便进行插入操作。接下来我们来看看如何实现。
6.4.1 链式队列的定义及初始化
typedef struct LinkNode
{
ElemType data;
struct LinkNode* next;
}LinkNode;
typedef struct
{
LinkNode* front, * rear;
}LinkQueue;
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
对于初始化来说,代码实现如下:
void InitQueue(LinkQueue& Q)
{
Q.front = Q.rear = new LinkNode;
Q.front->next = NULL;
}
- 1
- 2
- 3
- 4
- 5
6.4.2 入队
链式结构入队只需在添加结点于队尾元素之后,更改队尾指针指向即可。
//入队
void EnQueue(LinkQueue& Q, ElemType x)
{
LinkNode* s = new LinkNode;//生成一个新结点
s->data = x;
s->next = NULL;
Q.rear->next = s;//新结点插入rear之后
Q.rear = s;//修改rear指针位置
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
6.4.3 出队
//出队
bool DeQueue(LinkQueue& Q, ElemType& e)
{
if (Q.front == Q.rear)
return false;
LinkNode* p = Q.front->next;
e = p->data;
Q.front->next = p->next;
if (Q.rear == p)
Q.rear = Q.front;
delete(p);
return true;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
6.5 循环队列和链式队列的对比
对于循环队列和链式队列来说,在时间复杂度上它们的基本操作都是常数时间,即都为O(1)。而对于空间上来说,循环队列一开始长度就定死,而链式队列则较为灵活。所以我们可以总结如下:
在可以确定队列长度最大值的情况下,建议用循环队列。如果无法预估队列长度,则建议用链队列。
文章来源: blog.csdn.net,作者:ArimaMisaki,版权归原作者所有,如需转载,请联系作者。
原文链接:blog.csdn.net/chengyuhaomei520/article/details/123046312
- 点赞
- 收藏
- 关注作者


评论(0)