致谢

闵氏距离_百度百科 (baidu.com)

机器学习之KNN（k近邻）算法详解_平原的博客-CSDN博客_knn

鸢尾花(Iris)数据集_qinzhongyuan的博客-CSDN博客_鸢尾花数据集下载

致歉

前面发布的这一篇老版博客出现了一些脑子抽风的问题，现已修改完毕。

4 KNN算法

我们前面在第二讲的时候提到了线性回归，虽然市面上很大部分上的书都是先讲线性回归，但我更愿意先和你讲讲最简单的分类算法——KNN算法。它是一种能够找到相似对象的一个算法，这些对象彼此之间的关系比其他群组对象之间的关系更为密切。

4.1 sklearn转换器和估计器

4.1.1 转换器

在前一讲的特征工程中，我们一直在做一件事。通过实例化一个转换器类，然后将输出传入该对象，最后得出一个处理好的结果。

当我们处理数据时，通常都是调用转换器对象中的fit_transform方法，实际上，这个转换器方法可拆解为两个过程，一个是fit，一个是transform。

举标准化的过程为例，我们要做的是$(x-mean)/std$。而在这个过程中，fit步骤在计算mean平均值和计算std标准差，而transform步骤在计算总结果。

4.1.2 估计器

在sklearn中，估计器也是一个重要的角色，其是一类实现了算法的API。

比如用于分类的估计器：

• sklearn.neighbors k-近邻算法
• sklearn.naive_bayes 贝叶斯
• sklearn.liner_model.LogisticRegression 逻辑回归
• sklearn.tree 决策树和随机森林

比如用于回归的估计器：

• sklearn.linear_model.LinearRegression 线性回归
• sklearn.linear_model.Ridge 岭回归

再比如用于无监督学习的估计器：

• sklearn.cluster.KMeans 聚类

以上所有的估计器，实际上都是估计器类的子类。其皆继承于估计器类。

对于估计器父类来说，我们可以做这么一件事：

1. 实例化一个estimator类
2. estimator.fit(x_train,y_train)计算，当调用完毕，模型就会生成
3. 模型评估：score精度评估和predicct预测结果，其中如果想要比对真实值和预测值的差距，可以通过y_predict = estimator.predict(x_test)，将测试集放于预测函数中，预测出相应的结果，预测出来的结果可以用布尔函数与y_test作比对，看看是否分类正确。而如果想要计算准确率，可以采用accuracy = estimator.score(x_test,y_test)的方法来查看预测的准确率。

既然我们前面提过，上面的估计器均是估计器的子类，那么意味着一些子类应该有以上的方法，在后面的学习中，我们会学着怎么去调用它们。

4.2 KNN算法

4.2.1 概述

KNN算法也叫K-近邻算法，记得我们上面提到的简短的定义吗？我们用一个例子来说明KNN算法到底在做什么一件事。

KNN（K-Nearest Neighbor）最邻近分类算法，其为数据挖掘分类（classification）技术中最简单的算法之一，其指导思想是”近朱者赤，近墨者黑“，即由你的邻居来推断出你的类别。

假设图上该红点离蓝色小男孩最近，小男孩位于朝阳区，那么我也判断该点处于朝阳区。这就是KNN最简单的一个大白话过程。

让我们重新看一下KNN的定义：如果一个样本在特征空间中的k个最相似（即特征空间中最邻近）的样本中的大多数属于某一个类别，那该样本也属于这个类别。

假如我们k值取1，那么只要该样本离哪个点最近，其就会被归属于哪一个类别。这样做虽然简单粗暴，但是却容易出现问题：该样本容易受到异常值的影响！所以使用合适的k值可以避免异常值的影响。

那么在以上的定义中，我们如何来确定样本和哪个点最近呢？用什么来度量这个距离呢？

我们常用欧式距离来度量上述的距离，欧式距离这个名词似乎很陌生，实际上，它就是我们高中学过的两点之间距离公式。在二维形式下，其公式为：$p=\sqrt{(x_2-x_1{)}^2+(y_2-y_1{)}^2}$。在三维形式下，其公式为：$p=\sqrt{(x_2-x_1{)}^2+(y_2-y_1{)}^2+(z_2-z_1{)}^2}$。照此规律，我们可以推广到n维空间中。

除了上述的欧式距离外，还有一种距离——曼哈顿距离，曼哈顿距离也叫出租车几何距离，其由十九世纪的赫尔曼、闵可夫斯基所创，其距离计算公式为：$p=|X_1-X_2|+|Y_1-Y_2|$，照此规律，我们也可以推广到n维空间中。

上述两种距离实际上是闵可夫斯基距离的特殊情况，关于闵可夫斯基的数学细节，有兴趣的小伙伴可以上百度查找。

4.2.2 电影类型分析

我们再用一个例子来体会K近邻算法的应用。假设我们现在有几部电影：

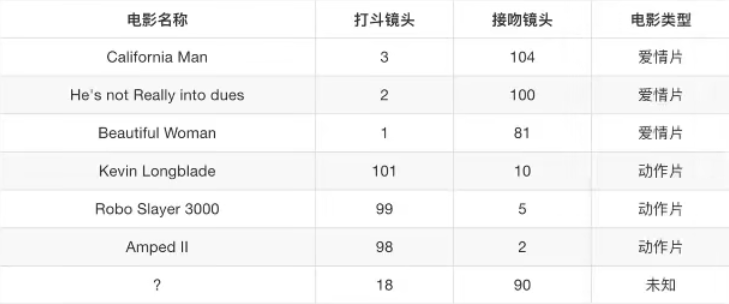
在上图的案例中，？位置电影是不知道其类别的，根据KNN算法，我们计算器距离。

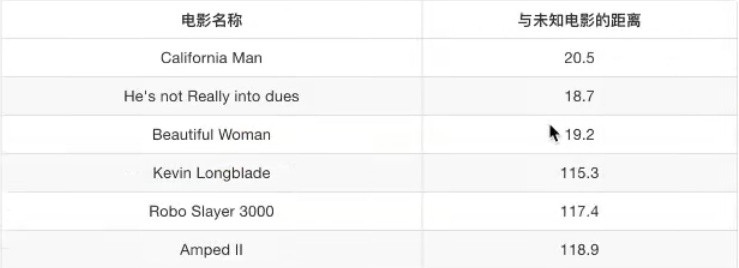
在以上的距离中，明显地，？离He’s not Really into dues最近，而这个电影为爱情片，？在KNN分类下k = 1时属于爱情片。

当k >= 2时，由于？受到多个点的共同作用，所以可能出现几个点是爱情片几个点是动作片的情况。这个时候如果想要确定样本点的类别，其遵循多数表态原则。就要看靠近k个点中，哪个类别的点比较多就为哪个类别，需要注意的是，如果k个点中各个类别的点数目一样多，那么该样本点即无法分类。也就是说，k如果取的太大，则样本点容易分错类。

多数表态原则

k近邻法中的分类决策规则往往是多数表决，即由输入实例的k个邻近的训练实例中的多数类决定输入实例的类。

让我们来总结一下上述讲的关于k值的选取问题。如果选择较小的k值，就相当于用较小的领域中的训练实例进行预测，“学习”的近似误差会减小，只有与输入实例接近的（相似的）训练实例才会对预测结果起作用。但缺点是“学习”的误差会增大，预测结果会对近邻的实例点非常敏感。如果邻近的实例点恰巧是噪声，预测就会出错。换句话说，k值的减小就意味着整体模型变得复杂，容易发送过拟合。

过拟合问题在线性回归后面的代码实现我会重新讲到，这里稍微提一下就是，当过拟合出现时，用于训练模型的训练样本点会准确无误的拟合训练出来的函数，这样做可以使训练集对训练函数拟合度高，但是预测结果却很差。

如果选择较大的k值，就相当于用较大领域中的训练实例进行预测。其优点是可以减少学习的估计误差，但是缺点是学习的近似误差会增大。这时与输入实例较远的训练实例也会对预测起作用，使预测发生错误。

k值一般是采用k折交叉验证来选取最优k值，在后面的学习中，我们会提到交叉验证，现在仅做了解。

4.2.3 算法实现

说完了上面的理论知识，我们理所应当要会写出代码来了。我们采用的是如下API：

sklearn.neighbors.KNeighborsClassifier(n_neighbors = 5,algorithm = ‘auto’)

n_neighbors：其可填一个int类型，表示默认查询邻居数

algorithm:{‘auto’,‘ball_tree’,‘kd_tree’,‘brute’}：除了auto之外，其余三个选项分别是用不同的数据结构来实现搜索邻居的方式，而使用auto就可以让传递给fit方法的值来决定最合适的算法。

光说不练假把式，我们今天就先拿KNN开刀，用我们之前所学工具斩落这员大将。

我们这里使用的是鸢尾花数据集，其详细数据如下：

iris_training.csv训练数据集，120条样本数据；iris_test.csv测试数据集，30条数据。本文只用到训练数据集，其中有花萼长度（Sepal Length）、花萼宽度（Sepal Width）、花瓣长度（Petal Length）、花瓣宽度（Petal Width）四个属性。标签0、1、2分别表示山鸢尾（Setosa）、变色鸢尾（Versicolor）、维吉尼亚鸢尾（Virginical）。

我们要做的步骤是：

• 获取数据集
• 数据集划分
• 特征工程——标准化
• 机器学习训练——KNN预估器流程
• 模型评估

代码实现如下：

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier


def knn_iris():
    """用KNN算法对鸢尾花进行分类"""
    # 1 导入数据集
    iris = load_iris()

    # 2 划分数据集
    x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state=6)

    # 3 特征工程：标准化
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.transform(x_test)

    # 4 实例化KNN算法预估器
    estimator = KNeighborsClassifier(n_neighbors=3)
    estimator.fit(x_train, y_train)

    # 5 模型评估
    # 方法1 直接比对真实值和预测值
    y_predict = estimator.predict(x_test)
    print("y_predict:\n", y_predict)
    print("直接对比真实值和预测值：\n", y_test == y_predict)

    # 方法2 计算准确率
    score = estimator.score(x_test, y_test)
    print("准确率为：\n", score)


# 调用方法
knn_iris()

我们知道，KNN方法在确定分类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。KNN方法在类别决策时，只与极少量的相邻样本有关。由于KNN方法主要靠周围有限的邻近的样本，而不是靠判别类域的方法来确定所属类别的，因此对于类域的交叉或重叠较多的待分样本集来说，KNN方法比其他方法更为适合。

平时，KNN算法的精度常常不如一些先进的模型，但是我们比如现在拿到了一个学习任务，需要选择一个学习器去解决问题，而且没有任何对该问题的前车之鉴，那么有时候可能会无从下手。通常我们不需要一上来就用一个神经网络或者强大的集成学习模型去做，而是可以用一用简单的模型做一个试探，KNN就是一个非常好的试探。

我们前面已经说过，KNN本质上属于懒惰学习的代表，也就是说它根本就没有用训练数据去拟合一个什么模型，而是直接用k个近邻的样本点做了个投票就完成了分类任务，那么如果这样一个懒惰模型在当前的问题上就已经能够得到一个较高的精度，则我们可以认为当前的学习任务是比较简单的，不同类别的样本点在特征空间中的分布较为清晰，无需采用复杂模型。

反之，若KNN得到的精度很低，则传达给我们的信息是：该学习任务有点复杂。往往伴随着的消息就是，当前问题中不同类别样本点在特征空间中分布不是清晰，通常是非线性可分的，需要我们去调用更强大的学习器。

虽然我们说在训练模型，可实际上，KNN完全没有真正意义上地训练模型，而只是单纯地分类罢了。

文章来源: blog.csdn.net，作者：ArimaMisaki，版权归原作者所有，如需转载，请联系作者。

原文链接：blog.csdn.net/chengyuhaomei520/article/details/123313146