致谢

导数与微分到底有什么区别？ - 知乎 (zhihu.com)

4 补充知识

在这一小节的学习中，我们会对上一小节的知识点做一个补充，并且拓展一个torch的模块。

4.1 微积分

4.1.1 导数和微分

在一元函数里，可导和可微是一回事，但是其表达的内涵不同。在下面的学习中，让我们先看看什么是导数。

假设我们现在有一个函数f(a) = 3a，它是一条直线。

如果a = 2，那么理所当然f(a) = 6，如果我对a做一个小小的增加，比如说增加0.001，小到我自己都看不出来，那么f(a)就会变为6.003，我们会发现，因变量受自变量3倍的影响，这就是导数。导数实际上就是函数的斜率。但是我们这里的函数是一条直线。在讨论曲线的导数时，我们一般是讨论某个点的导数。一个等价的导数表达式可以这样写$f^{\prime }(a)=\frac{d}{da}f(a)$。不管你是否将𝑓(𝑎)放在上面或者放在右边都没有关系。

1. 导数就是斜率，而曲线函数的斜率，在不同的点是不同的。
2. 如果想知道一个函数的导数，你可以参考下面的导数公式。

拓展：导数公式

导数公式

1. y=c(c为常数) y’=0
2. $y=x^n$ $y^{\prime }=n{x}^{n-1}$
3. $y=a^x$ $y^{\prime }=a^{x}lna$
4. $y=e^x$ $y^{\prime }=e^x$
5. y=logax $y^{\prime }=logae/x$
6. y=lnx $y^{\prime }=1/x$
7. y=sinx $y^{\prime }=cosx$
8. y=cosx $y^{\prime }=-sinx$
9. y=tanx $y^{\prime }=1/co{s}^{2}x$
10. y=cotx $y^{\prime }=-1/si{n}^{2}x$

有时候，一个函数并不是基本的函数，而是由多个函数组合而成，这时候我们就需要一些运算法则来帮我们解决其求导的问题了。

• 减法法则：$(f(x)-g(x){)}^{\prime }=f^{\prime }(x)-g^{\prime }(x)$

• 加法法则：$(f(x)+g(x){)}^{\prime }=f^{\prime }(x)+g^{\prime }(x)$

• 乘法法则：$(f(x)g(x){)}^{\prime }=f^{\prime }(x)g(x)+f(x)g^{\prime }(x)$

• 除法法则：$(g(x)/f(x){)}^{\prime }=(g^{\prime }(x)f(x)-f^{\prime }(x)g(x))/(f(x){)}^2$

4.1.2 偏导数

如果只是对一个变量求导，形如$y=2x+1$，那么对x求导的话，实际上就是对一个变量求导，而在多元函数微分学中，我们常常会遇到多变量的情况，此时我们就要用到偏微分，也就是偏导数。

在深度学习中，函数通常依赖许多变量，所以偏导数也及其重要。

求偏导的时候，把要求导的变量像平时那样求导，把不求导的变量看成常数即可。

4.1.3 梯度

我们把某一个多元函数对其所有变量的偏导数用向量框起来，这就是我们所说的关于该函数的梯度向量，口头上简单说成梯度。

如果说一个函数时y = $a{x}_1+b{x}_2+...$

那么该函数的梯度即为：${\nabla }_{x}f(x)=[\frac{\partial f(x)}{\partial x1},\frac{\partial f(x)}{\partial x2},\dots ,\frac{\partial f(x)}{\partial xn}{]}^T$

其中${\nabla }_{x}f(x)$通常在没有歧义时被$\nabla f(x)$取代

4.1.4 链式求导

多元函数通常是复合的，所以我们可能没法应用上述任何规则来微分这些函数。所以，我们需要链式法则使我们能够微分复合函数。

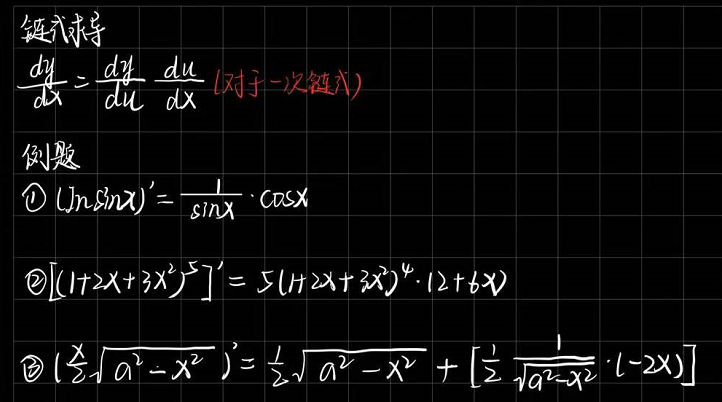
4.2 Hub模块

根据深度学习的发展，各类大牛在许多的论文上提出了十分优秀的神经网络模型。而这些模型大多都被收集于torch.hub之中。通过下列的代码可以查看hub中存放的模型。

torch.hub.list('pytorch/vision:v0.4.2')

  

 

  
1
 

其余的这里我就不做过多介绍了，因为Github上的pytorch.hub上有详细说明，甚至导入方式，返回什么都写的十分的详细。还有很多实际的例子和案例可供选择，感兴趣的小伙伴可以去试试。

试试归试试，但是在学习的阶段中，我们十分不建议去调别人的模型用于自己的使用，我们应该做的是，从0搭建，这样才体现学习的目的。

文章来源: blog.csdn.net，作者：ArimaMisaki，版权归原作者所有，如需转载，请联系作者。

原文链接：blog.csdn.net/chengyuhaomei520/article/details/123708608