致谢

逻辑回归为什么用Sigmoid？ - 知乎 (zhihu.com)

逻辑回归中的损失函数的解释_yidiLi的博客-CSDN博客_逻辑回归损失函数

11 逻辑回归

逻辑回归也被称为逻辑斯蒂回归(Logistic Regression)，虽被称为回归，但是其实际上是统计学习中经典的分类方法。

逻辑回归常常被用于二分类问题，比较常见的有：

1. 判断一封电子邮件是否是垃圾邮件；
2. 判断一次金融交易是否是欺诈；
3. 区别一个肿瘤是恶性的还是良性的

我们将因变量可能属于的两个类分别称为负向类和正向类，则因变量y∈0，1。其中0表示负向类，1表示正向类。实际上，哪个是正向类哪个是负向类其实并不重要。虽然没有特别界限，但是我们通常把0归结为没有，而1归结为具有我们要寻找的东西。

11.1 引入

对于二分类问题，y取值非0即1；但如果你使用的是线性回归，那么其输出的$\hat{y}$可能远远大于1或者为负数。所以如果我们用线性回归来做分类，效果实际上是很差的。

逻辑回归是怎么把输出变成0到1之间的呢？实际上，它拿线性回归的输出作为输入，然后用函数$g(x)=\frac{1}{1+e^{-x}}$输出，其输出值可以把线性回归的结果投射到0和1的区间上。

11.2 激活函数

上面我们说到将线性回归的输出输入到一个函数上再输出，这样能够使结果投射到0-1的区间上。在深度学习中，我们常常把这类可以将线性回归的结果投射到某个区间函数叫做激活函数，而上面提到的我们通常称为sigmoid激活函数，在深度学习中，我们会陆续见到其他的激活函数。

实际上，为何逻辑回归要用sigmoid函数来投射线性回归的结果是有原理的，如果感兴趣可以去网上搜索相关推导，如果我不懒后续也会手推，但是你现在需要知道的一点是——当因变量服从伯努利分布(0-1分布)时，广义线性模型就为逻辑回归。

实际上，逻辑回归用于二分类问题，而其实际上是softmax回归的特殊情况，softmax回归常常用来解决多分类问题，在后续深度学习的文章中，我们会持续了解它们。

让我们看一下sigmoid激活函数长什么样吧！

import matplotlib.pyplot as plt
import math
import numpy as np
import matplotlib

matplotlib.rcParams['font.family'] = 'SimHei'
matplotlib.rcParams['axes.unicode_minus'] = False


# 1 准备数据
def func(x):
    y = 1 / (1 + math.exp(-x))
    return y


X = np.linspace(-100, 100, 200)
Y = [func(x) for x in X]
# 2 创建画布
plt.figure()

plt.grid(True, linestyle='--', alpha=0.5)

# 3 画图
plt.plot(X, Y)

# 4 设置标题
plt.title("sigmoid函数图像")

# 5 释放图像
plt.show()

out：

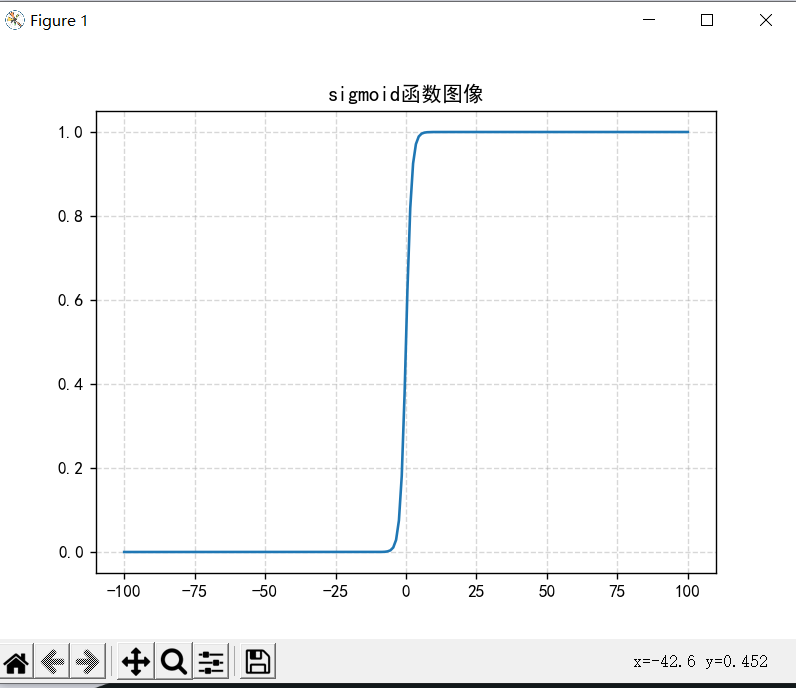
实际使用中，我们默认分类的界限是0.5，也就是说经由sigmoid函数投射值如果大于0.5则直接分为1类，否则分为0类。

11.3 损失函数

记得我们前面谈到线性回归的损失函数吗，由于线性回归属于回归问题，所以输出是某一个预测值，我们拿预测值和真实值进行比对来衡量其误差，这个比对方式，我们用的是平方损失函数。但是在逻辑回归中，我们并不能继续这么做了，因为逻辑回归非0即1，你还拿平方损失函数比对其误差，如果没有误差，那不就是0吗，这还搞啥子，我们后面还要采用梯度下降呢，参数不动这模型还怎么优化。

为此，我们急需有一个新的损失函数来取代之前的平方损失函数。在逻辑回归中，我们常常使用对数似然损失函数来衡量损失。其公式为：
$$cost(h_0(x),y)=\{\begin{array}{rlrlr}-\log (h_0(x))& & if& & y=1\\ -\log (1-h_0(x))& & if& & y=0\end{array}$$
当y = 1时，我们可以观察其函数图像，如下所示：

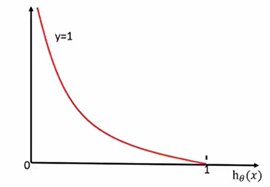
明显地，如果$h_0(x)$越接近1，而我们y = 1，那么说明我们分类地越准确。

同理，当y = 0时，我们也可以观察其图像，如下所示：

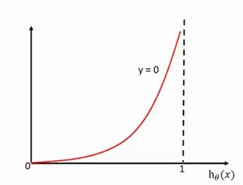
当$h_0(x)$越接近于1，而我们y = 0，说明我们分类的很差，损失很大。

为了后续计算梯度下降方便，我们必须对上述的分段函数做一个简化。为此，我们将其形式改写为：
$$cost(h_0(x),y)=\sum _{i=1}^m-y_{i}log(h_0(x))-(1-y_i)log(1-h_0(x))$$
这个公式的好处在于，当你的y取1，那么$-y_{i}log(h_0(x))$会保留，后面一部分会为0，这样就等同于上面的分段函数，当你的y取0，同理，$-y_{i}log(h_0(x))$会为0，后面一部分保留。

11.4 梯度下降

同样地，我们在打基础阶段还是照样使用梯度下降来优化损失函数，从而找到逻辑回归中的权重参数。

除了梯度下降算法以外，还有一些常被用来令代价函数最小的算法，这些算法更加复杂和优越，而且通常不需要人工选择学习率，通常比梯度下降算法要更加快速。这些算法有：共轭梯度(Conjugate Gradient)，局部优化法(Broyden fletcher goldfarb shann,BFGS)和有限内存局部优化法(LBFGS)。

11.5 案例：癌症分类预测

让我们来看看sklearn为我们提供的API。

sklearn.linear_model.LogisticRegression(solver = ‘liblinear’,penalty = ‘l2’,C = 1.0)

• solver：优化求解方式。默认使用开源的liblinear库实现优化，内部使用了坐标轴下降法来迭代优化损失函数
• penalty：正则化种类
• C：正则化力度

在之前的学习中，我们一直用着sklearn自带的数据集。是的，它们是好用，这仅仅只是因为人家帮你预处理好了，他在帮你偷懒！所以，我想你是时候学着处理一些东西了。

我们先去UCI把我们要用到的数据集下载下来，或者你也可以不下载，直接利用pandas读取网站即可：索引 /ml/机器学习数据库/乳腺癌-威斯康星州 (uci.edu)

其中数据放于http://archive.ics.uci.edu/ml/machine-learning-databases/breast-cancer-wisconsin/breast-cancer-wisconsin.data

而数据介绍放于http://archive.ics.uci.edu/ml/machine-learning-databases/breast-cancer-wisconsin/breast-cancer-wisconsin.names

我们先来读取数据。由于原始数据是没有标签的，所以我们顺便给数据打上标签。

import pandas as pd
import numpy as np

# 1 读取数据
path = "http://archive.ics.uci.edu/ml/machine-learning-databases/breast-cancer-wisconsin/breast-cancer-wisconsin.data"
colum_name = ['Sample code number', 'Clump Thickness',
              'Uniformity of Cell Size', 'Uniformity of Cell Shape',
              'Marginal Adhesion', 'Single Epithelial Cell Size', 'Bare Nuclei',
              'Bland Chromatin', 'Normal Nucleoli', 'Mitoses', 'Class']
data = pd.read_csv(path, names=colum_name)

从原数据集上看，数据中有？，我们在数据预处理中通常先将其替换为NaN，然后进行删除。如果你喜欢填充往?部分填充均值也是可以的。

# 2 缺失值处理
data = data.replace(to_replace = "?",value = np.nan)
data.dropna(inplace = True)

处理完成后，我们可以通过直接查看数据看看是否处理成功，也可以通过ifnull()函数查看是否还有空值。

pd.set_option('display.max_rows', None) # 显示所有行
data

data.isnull().any()

看到没有空值后，我们下一步要对原始数据集进行特征和分类标签的分离。

# 3 划分数据集
from sklearn.model_selection import train_test_split

# 筛选特征值和目标值
x = data.iloc[:,1:-1]
y = data["Class"]
x.head()

然后进行切割数据集。

# 划分数据集
x_train,x_test,y_train,y_test = train_test_split(x,y)
x_train.head()

逻辑回归本质上属于广义线性模型，所以我们还要进行一下标准化。

# 4 标准化
from sklearn.preprocessing import StandardScaler
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)
x_train

标准化完成后，我们调用逻辑回归预估器进行模型的训练：

# 5 逻辑回归
from sklearn.linear_model import LogisticRegression
estimator = LogisticRegression()
estimator.fit(x_train,y_train)

我们可以看一下训练后的回归系数和偏置。

# 回归系数和偏置
estimator.coef_

estimator.intercept_

最后我们对模型进行评估。

# 6 模型评估
y_predict = estimator.predict(x_test)
print("y_predict:\n",y_predict)
print("直接比对真实值和与预测值：\n",y_test == y_predict)

score = estimator.score(x_test,y_test)
print("准确率为：\n",score)

文章来源: blog.csdn.net，作者：ArimaMisaki，版权归原作者所有，如需转载，请联系作者。

原文链接：blog.csdn.net/chengyuhaomei520/article/details/123636629