线性代数(二)

2 解线性方程组

1 Ax = b的列图像实质是A的列向量有各种线性组合，b为其中的一种组合结果。

2 Ax = b可以写为$Ax=x_1{a}_1+...+x_n{a}_n=b$，其中$a_1,a_2...a_n$为A中的列向量。

3 当Ax = 0时，x有一个取值方式为0向量。

4 若A中有三条列向量，任意一条向量可以由另外两条向量所表示时，我们说该矩阵为奇异矩阵。

5 列图像可以用于解决矩阵乘法

在这一讲中，我们着重要谈论的是关于解方程组的问题。我们先来看下面这样一组等式。

两个方程两个未知数
$$\begin{gathered} 2x-y=0 \\ -x+2y=3 \end{gathered}$$

我们想要解这个方程组，如果按照高中学过的知识，我们会将其直接消元或变量代换，解出其方程。

通过简单的计算，我们很容易得到问题的解：x = 1,y = 2。

实际上，我们可以用矩阵的形式来表示上面的方程组。如我们把方程组中未知数的系数全部提取，然后用一个中括号括起，就可以得到一个系数矩阵。
[ 2 − 1 − 1 2 ] \left[

2.1 行图像

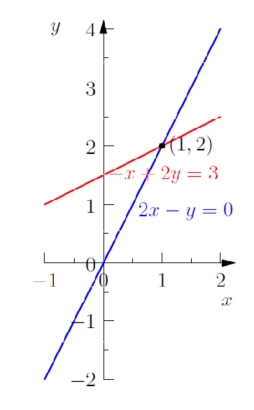
行图像(row picture)为行视角下的图像。我们把一条方程看做一条直线，那么在二维直角坐标系中我们可以轻松地画出方程组的图像。

我们可以很快画出以上的图像，这是一个学生应有的基本素养。

从图像上我们可以看到，对于两方程来说，其解即为行视角下两条直线的交点，即(1,2)为两方程的解。

2.2 列图像

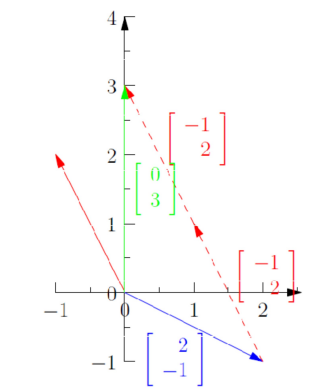
让我们以列图像(column picture)的方式思考一次。

我们可以将上述的方程按照列向量的形式来写出。
x [ 2 − 1 ] + y [ − 1 2 ] = [ 0 3 ] x\left[

让我们试着以向量的形式将上述的列视角观点画于图像之中。

从图像上看也能验证我们上述的观点。

我们不妨想象。在列图像中，如果col1和col2分别为A中的两条列向量，且它们不共线，那么对于整个平面直角坐标系上的任意一条向量，都可以用col1和col2表示。

换而言之，对于 x [ 2 − 1 ] + y [ − 1 2 ] x\left[

2.3 三维情况

我们不妨将上述的二维情况推至三维。

三个方程三个未知数
$$\begin{gathered} x+2y+3z=6 \\ 2x+5y+2z=4 \\ 6x-3y+z=2 \end{gathered}$$

xyz三个未知数可以是不存在的，但是对于本例来说它是存在的。

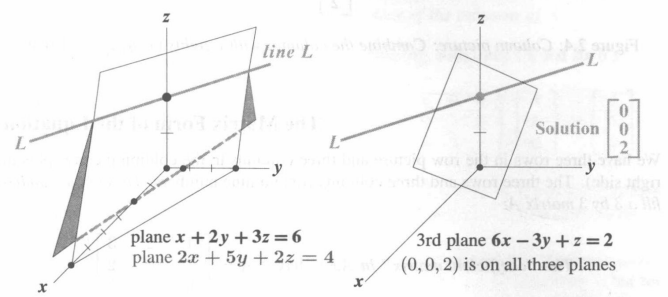
同样地，我们可以将画出上面的行图像。

从图像上不难看出，我们在高维度时最好不要往行视角的方向考虑，因为行图像很难画。

我们不妨从列视角的角度去考虑上面的方程组。
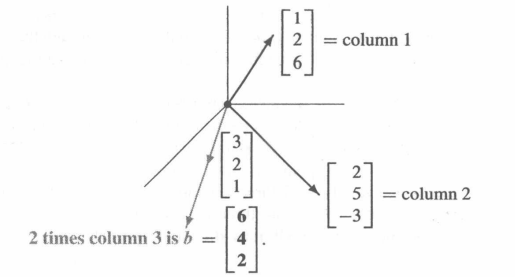
x [ 1 2 6 ] + y [ 2 5 − 3 ] + z [ 3 2 1 ] = [ 6 4 2 ] x\left[

通过计算，我们可以知道(x,y,z) = (0,0,2)。

2.4 奇异

我们来思考这样一个问题，当处于三维情况时，我们有Ax = b。那么对于任意的b，是否都能求解Ax = b？

或许我们可以换种问法，对于上述列向量的线性组合，是否能覆盖着整个线性空间。

答案明显是否定的，假如有三条列向量col1,col2,col3。且三条向量均处于同一个平面，此时对于Ax来说，无论如何组合，其得出的新向量都只会在三条列向量所处的平面中，而不会逃离平面。我们把这种情况称为奇异，而把Ax对应的系数矩阵A称为奇异矩阵。

奇异矩阵的研究有多种特殊情况，故在最开始时，我们先暂时不关注奇异问题。

2.5 等式的矩阵形式

我们前面谈论过方程组可以写为矩阵形式。
[ 2 − 1 − 1 2 ] [ x y ] = [ 0 3 ] \left[

在后面的章节中，我们会提供多种方法供矩阵相乘，现在让我们先用几个老方法来解决这个问题。

2.5.1 点积

我们可以采取点积的形式来完成矩阵的乘法，演示如下：
[ 2 5 1 3 ] [ 1 2 ] = [ 2 × 1 + 5 × 2 1 × 1 + 3 × 2 ] = [ 12 7 ] \left[

2.5.2 转换为列图像处理

我们可以可以把矩阵相乘用列视角的观点来看待，演示如下。
[ 2 5 1 3 ] [ 1 2 ] = 1 [ 2 1 ] + 2 [ 5 3 ] = [ 2 1 ] + [ 10 6 ] = [ 12 7 ] \left[

文章来源: blog.csdn.net，作者：ArimaMisaki，版权归原作者所有，如需转载，请联系作者。

原文链接：blog.csdn.net/chengyuhaomei520/article/details/124225302