8 树(上)

8.1 引入

我们在前面的章节中一直在谈一对一的线性结构，可现实中，还有很多一对多的情况需要处理。

一对一和一对多

为什么说前面学习的是一对一的线性结构？从顺序表中我们可以看出，一个结点总是跟在一个结点的后面，栈、串、队列也皆是如此，故我们说它们都是一对一的线性结构。

可是树却不是一对一的线性结构，因为对于树来说，其一个结点的后面可能跟着多个结点，故它是一种一对多的线性结构。

8.2 树的基础知识

我们来讨论一下树。

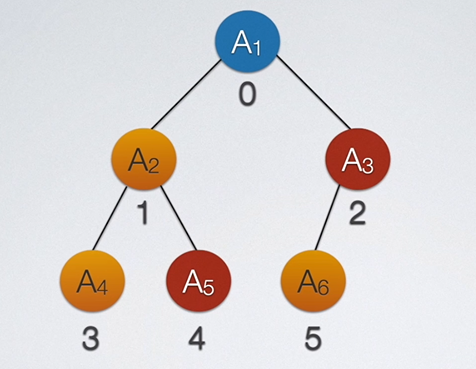
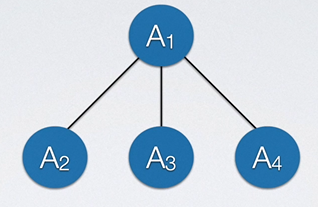
物如其名，树结构看起来就像一颗倒挂的是树。树实际上也是一个递归结构，如果我们把A1称为父结点，则A1下的A2、A3、A4就是它的子结点。那么对于A1来说，其子结点有3个，对于A2来说，其也可能有子结点。

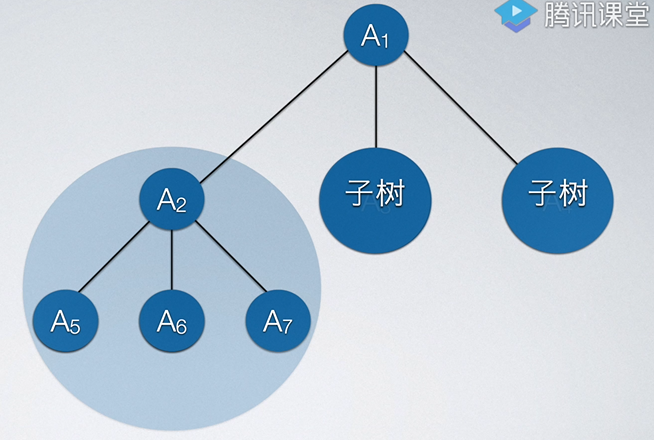
不同的术语

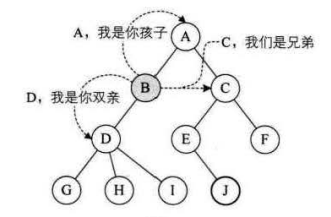
有时候，不同的教材不同的地方有不同的术语，如父子结点有时候也叫做双亲和孩子。

我们把某一结点的分支数量叫做结点的度。对于上图，显然A1结点的度是3，A7结点的度为0。我们把整棵树中所有结点拥有的最大分支数称为树的度，如上图中树的度为3，因为遍历树中所有结点，度最大的那个结点度为3。

同理，在上图中，A5的祖先为A2和A1，A1的子孙为A2~A7。

一棵树可以分为多个层。如下图所示：

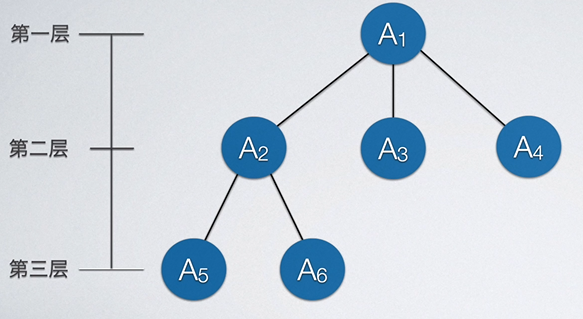
同一个双亲的结点互称兄弟，如A2可以是A3的兄弟结点，反过来A3是A2的兄弟结点这种表述也无误；树的层数叫做树的高度或深度，如上图中树的深度是3。结点从树的上面往下面数，第几层即为结点的深度；结点从下往上面数，第几层即为结点的高度。如A1，它从下往上数在第三层，故A1结点高度为3，而从上往下数第一层，故其深度为1。

树的叶结点指的是：若结点没有继续往下的分支了，那么该结点即为叶结点。如上图中A5，A6，A3，A4均为叶结点。

408科目10年05题

在一颗度为4的树T中，若有20个度为4的结点，10个度为3的结点，1个度为2的结点，10个度为1的结点，则树T的叶结点个数为？

• $10\ast 1(10个度为1)+1\ast 2(1个度为2)+10\ast 3(10个度为3)+20\ast 4(20个度为4)=122$
• $123(总节点数)=10+1+10+20+叶结点$

故叶结点数为82。

8.3 树的存储结构

通过对前面的学习，我们需要思考一下如何用代码实现树的顺序存储，树提供了三种表示方法，分别是双亲表示法、孩子表示法、孩子兄弟表示法。

8.3.1 双亲表示法

双亲表示法的重点在于，我们存储的内容不仅仅是结点的数据，而且还要存储其父节点是谁。故我们想到在结构体中定义两个数据，一个用于存结点数据，另一个用于存父节点在数组中的下标。

由于根结点是没有双亲的，故我们约定根节点的双亲位置设置为-1。如下图所示：

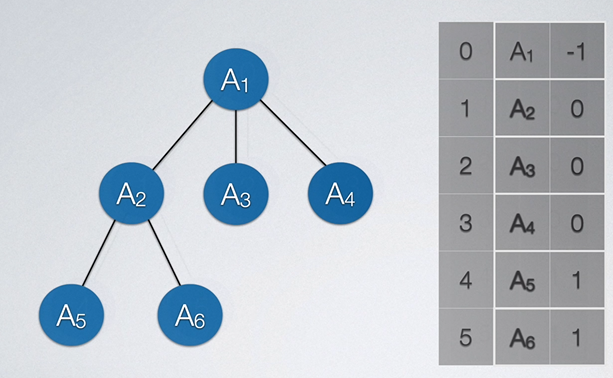
#define MAX_TREE_SIZE 100

//结点结构
typedef struct
{
	Elem data;//结点数据
	int parent;//双亲位置
}PTNode;

//树结构
typedef struct
{
	PTNode node[MAX_TREE_SIZE];
    int r,n;//根的位置和节点数
}

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
 

这样的存储结构有一个好处，我们可以根据结点中存储的双亲位置来找到它的双亲结点，但是问题是，如果你想要知道结点的孩子是什么就无能为力了，你得遍历整个结构。

8.3.2 孩子表示法

如果树中含有多颗子树，我们可以考虑使用多重链表。多重链表的意思就是每个链表节点中都包含有多个指针域，每个指针域指向子树的根节点。但是这种表示法有一个问题，就是每个子树的度是不一样的，有些子树的度是1有些是2甚至于度为0。

对于上述的问题我们有两种不同的方案。

方案一

我们直接可以让树的度作为指针域的个数。我们知道，树的度是树中所有结点的最大度数。这样的话子树的度小于树的度时，我们把其余的指针域置空即可。如下所示：

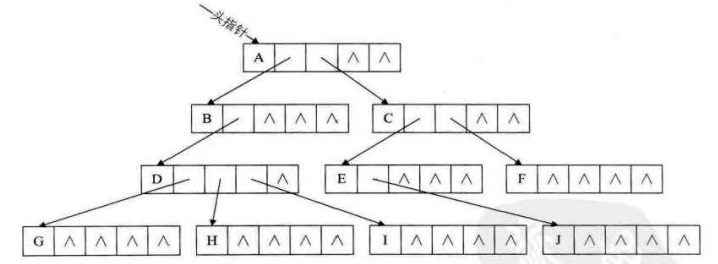
但是这种方案在于浪费内存。我们来看看方案二。

方案二

既然怕浪费，那我们就按需分配。

我们在结构体定义时多加一个整形类型的变量degree用于记录度域（即度的范围）。如下所示：

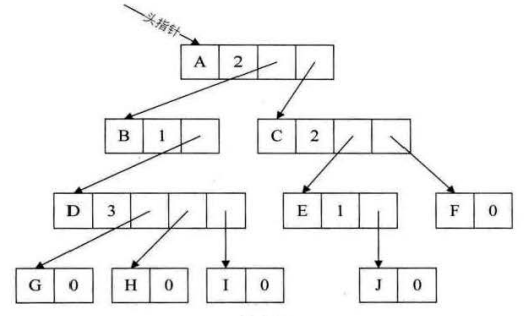
这种方案虽然避免了浪费空间，但是却浪费了时间，因为要维护度的数值。

既然上述方案都不太靠谱，我们就用方案3的孩子表示法吧。具体办法是，把每个结点的孩子结点排列，用单链表作为存储结构。如果是叶子结点则单链表为空。

以上的文字可能有点晦涩难懂，我们看图理解一下。

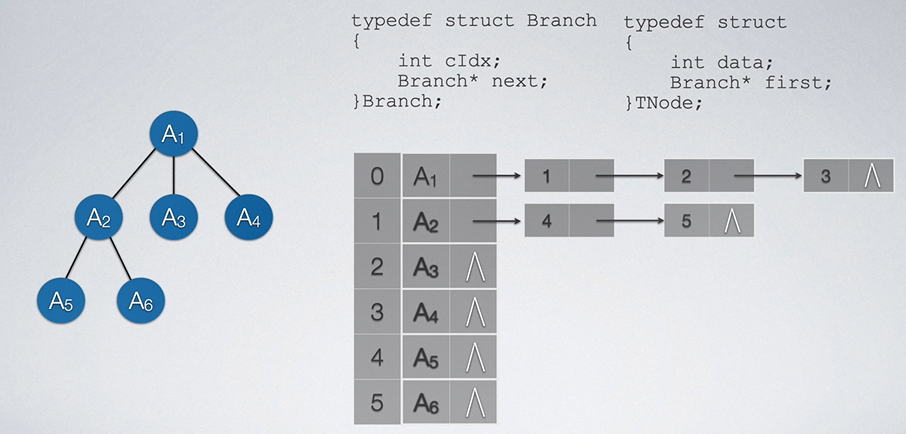
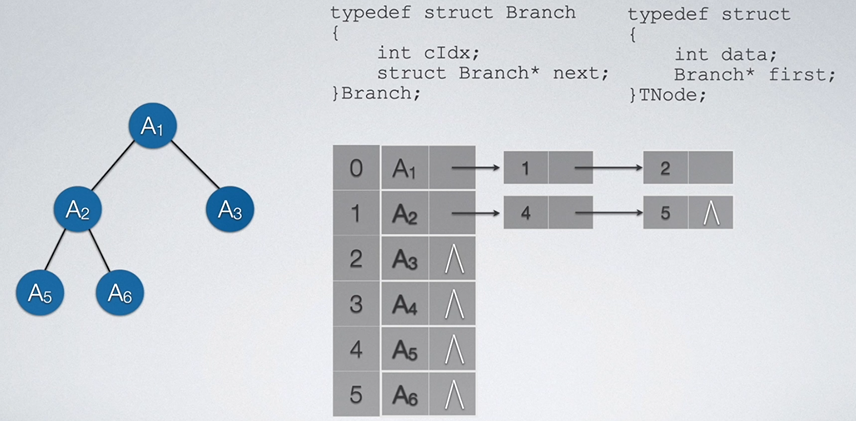
一开始我们用结构体定义两个变量。一个是结点数据，一个是指针域，其结构体看做是一个结点。而后将所有的结点存储一个数组中。如果一个结点有孩子，那么其指针域指向存放其孩子的链表，链表中存储的是关于该节点的所有孩子。

如上图所示，A1是有三个孩子A2、A3、A4，故其孩子链表中存放三个结点，孩子链表的头指针存于数组的0号位，数组的0号位存储的是一个结点的结构体，结构体中有A1和其孩子链表的头指针。

8.4 二叉树

8.4.1 基础知识

在8.3.2 讲的孩子表示法中，孩子链表中存储的结点是没有顺序之分的。也就是说，传统的树没有任何约束，度数可以任意，孩子之间也没有次序。

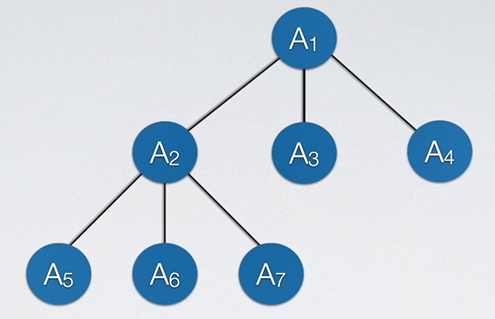
为此，我们引入了二叉树。二叉树规定每个节点的孩子最多只能有两个，即度数<=2；并且其孩子节点中，左边的孩子叫做左孩子，右边的叫右孩子。

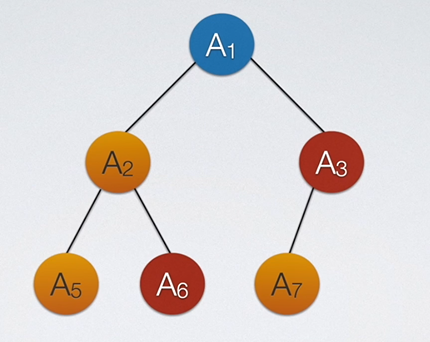
二叉树也可以有多种情况，如下图所示：

如果一颗二叉树是满的，比如一共三层，每层都是满的。如下图所示：

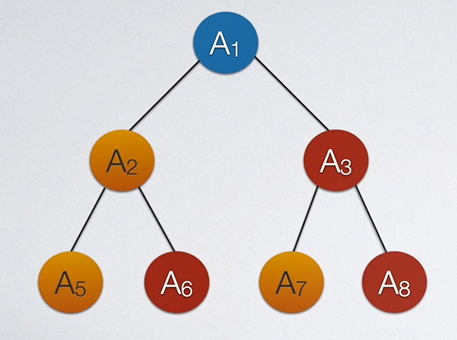
这个时候我们叫他满二叉树。

如果将一颗二叉树从下往上，总右往左删除，它们无论怎么删除，它都是一颗完全二叉树。

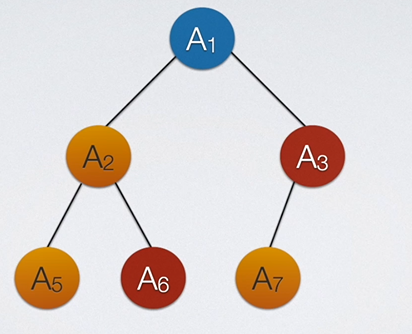
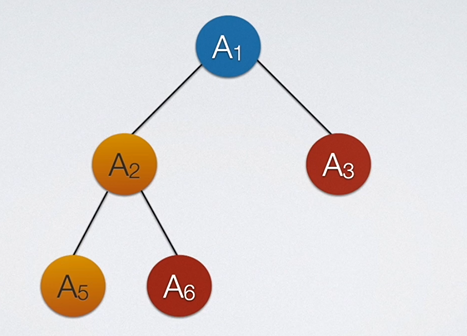
也就是说，如果一颗满二叉树少了A7但有A8，其他不变，那么这个二叉树就不是完全二叉树。并且，满二叉树可以看做是完全二叉树的特别版。

8.4.2 高频考点

第一个比较常考的是关于求完全二叉树的高度。完全二叉树的高度由二叉树中的结点个数来决定。为了方便讲解，我们先探究满二叉树的规律。通过列举或者通过高中的等比数列知识都是可以发现这个规律的。如下所示：

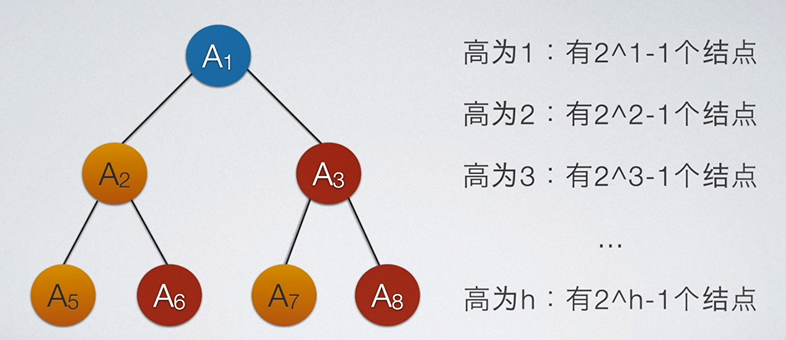
也就是说，一个高为h的满二叉树，其结点为$2^h-1$。那么，一个高位h的完全二叉树结点数肯定小于$2^h-1$且大于$2^{h-1}-1$。

我们可以将上述的不等式进行化简，如下所示：

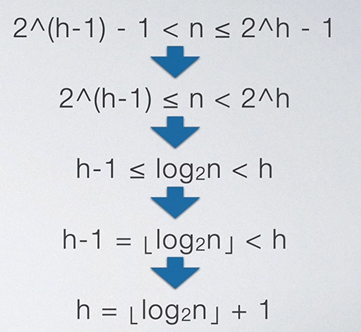
至此，我们可以导出完全二叉树的高度公式了。

有时候我们我们可能会见到不一样的公式，这是因为在上述化简第二步时选择直接把1扔掉还是通过计算同时+1的差异导致的。

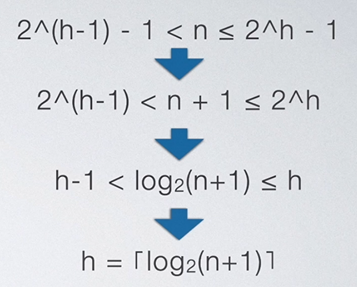
408科目09年05题

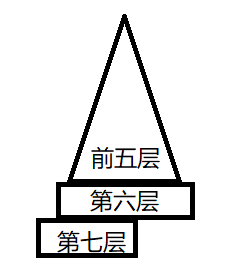
已知一颗完全二叉树的第6层(设根为第1层)有8个叶结点，则该完全二叉树的结点个数最多是？

考虑到最多，那么必然是这种情况：

也就是说，前五层结点数为：2^5-1 = 31，满6层的二叉树结点为2^6-1 = 63，故第六层结点数为63-31 = 32，又叶子结点为8，故非叶子结点有32-8 = 24，故这个完全二叉树的结点个数最多是：63+24*2=111个

8.4.3 二叉树的性质

最简单的，总分支数= 总结点数-1，这个很简单，对于传统的树也是同样满足的。

设分支数为i的结点数为$N_i$，则满足总结点数$N=N_0+N_1+N_2$。同样地，总分支数$N-1=N_1+2N_2$，这个在我们前面学基础知识时就已经提到过了。

对于上述的方程，我们可以解得$N_0=N_2+1$，故叶子结点数 = 双分支结点数+1，这是一个非常重要的结论。有时考题里面会说二叉树含有空分支，此时考题就更为灵活了，需要注意一下。

对于一颗存储在数组的完全二叉树来说。

父结点位置如果为i，则左孩子结点位置为2i+1；右孩子结点位置为2i+2。

以上的规律在不同的学校考题中有所不同，如果位序从1开始，则左孩子结点位置为2i；右孩子结点为2i+1。

8.4.4 二叉链表

对于二叉树的链式存储来说和树的链式存储并无二致，并且我们可以说明存放孩子结点的链表第一个结点为左孩子，第二个结点为右孩子，这完全没有问题。

但是我们可以回想我们使用孩子表示法的初衷。是由于每个子树度数的不确定性我们才使用这种方法，但是现在二叉树确定了，为何还要怎么搞，岂不大材小用?

我们不如回归本心，写一个结点结构体，结构体中含有左右子结点的指针域和结点所含数据，然后将所有结点放于数组中即可。

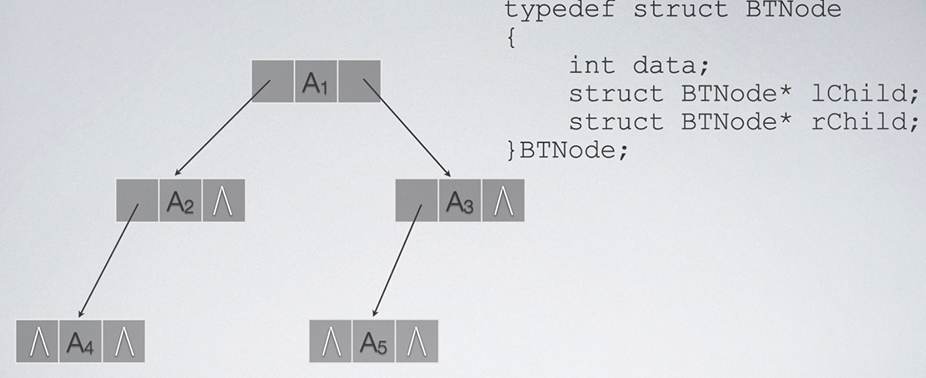
上述的结构我们称为二叉链表。

二叉链表实际上可以用在传统树的存储，因为在之前的孩子表示法设计中，某结点的孩子结点是作为链表接在结点的指针域中的，所有孩子结点不需要都和父节点有关系，只需要其中一个和父节点有关系即可。故我们可以改造传统树，变成二叉链表能够存储的样子：

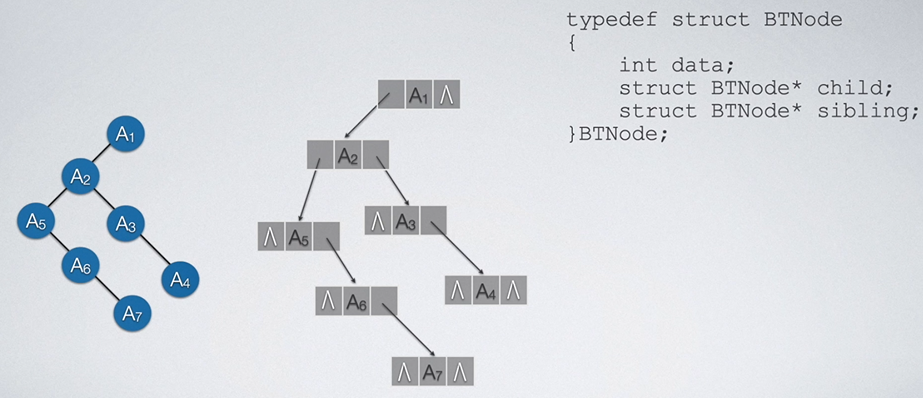
以上这种表示方法我们称为孩子兄弟表示法。

8.4.5 树和二叉树的转换

前面说过的转换我们只是口头讲述，并没有一种系统的方式来转换。

一种简单的方式是，将兄弟结点用一条线连起，然后只保留一条通往父节点的线，其他多余的线删除，如下图所示：

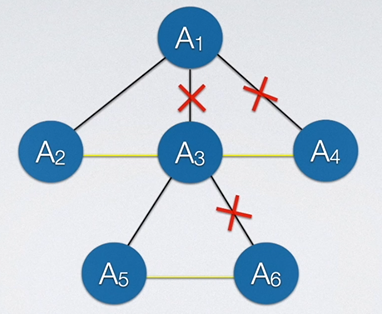
删除线后，我们把它掰成二叉树的模样即可。

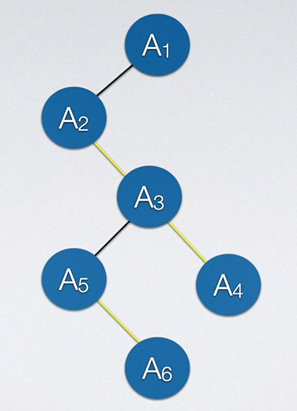
如果想要将二叉树转为树，只需要从根节点开始，一条路从头走到尾，途径的所有结点都加上一条线和根节点即可，对于其他剩余的结点在也可以用同样的操作。如下图所示：

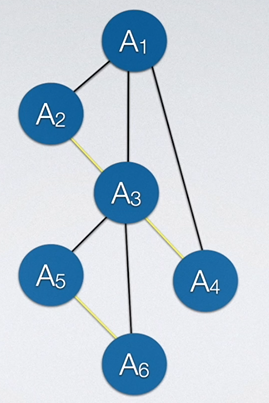
然后掰回树。

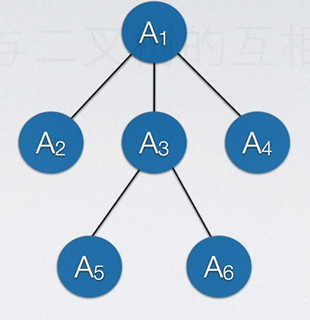
8.4.6 森林和二叉树的转换

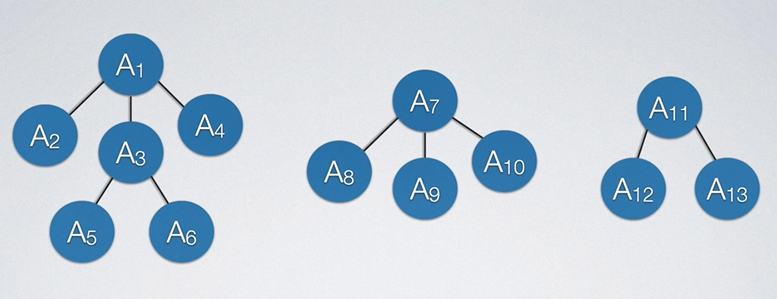
森林就是多棵树放在一起，如果想要转换为二叉树，只需将森林中的所有树先单颗转为二叉树。需要注意的是上图的第三颗树，它看起来像是二叉树，但我们不确定，故我们也要对他做转化的工作，全部转换后如下所示：

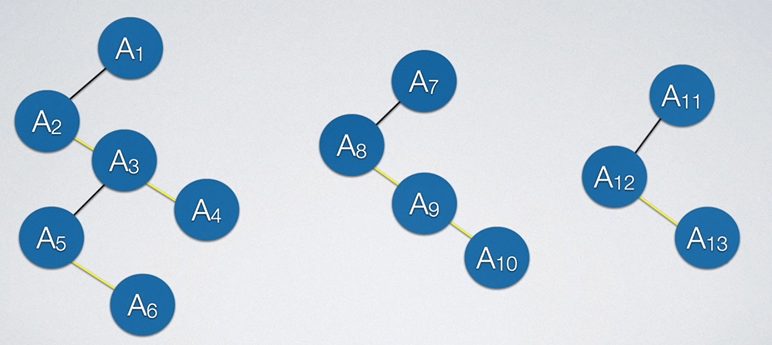
全部的单树转换为二叉树后，我们只需连接所有单树的根节点的右分支即可，如下所示：

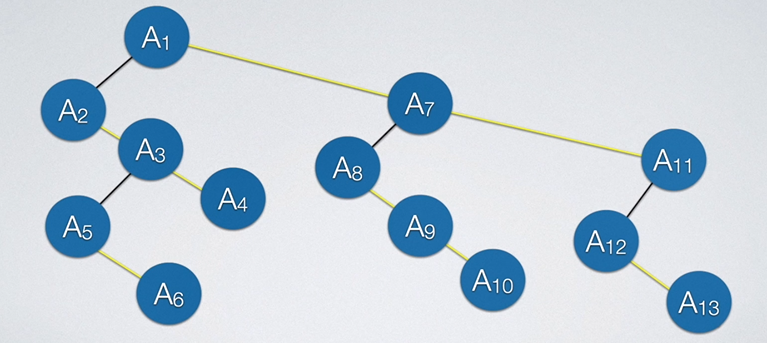
同理，如果想要将二叉树还原为森林，只需将右分支删掉，然后看看单树的根节点的右分支是否为空，非空则继续删掉右分支，为空则将所有单树还原为传统树即可。

408科目09年06题

将森林转换为对应的二叉树，若在二叉树中，结点u是结点v的父结点的父结点，则在原来的森林中，u和v可能具有的关系是？

我们可以画出可能的二叉树，如下所示：

然后将按上述的方法还原，结果u和v可能的关系有父子关系和兄弟关系。

8.5 遍历

遍历一词在如今才出现，为何前面我们不提遍历？因为前面一对一的线性结构的遍历过于简单，只需从头到尾走一遍即可。

但是对于一对多的树，我们要如何去遍历它呢？

以二叉树为例，我们需要制定一定的规则来访问。第一个遍历的想法是，我们从上到下，从左到右进行遍历，如图所示：

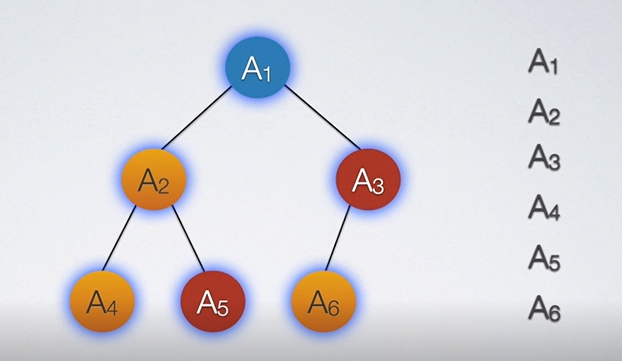
以上提到的这种思路我们叫做层次遍历，也叫广度优先遍历。

我们还有第二种想法，我们称为深度优先遍历。其又细分为先序、中序和后序遍历。

让我们来体会一下这个想法是怎么实现的。如下图所示：

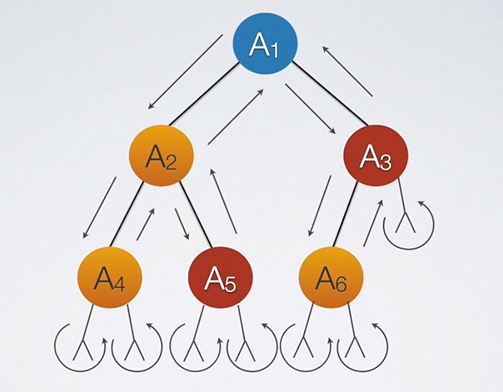
在这个过程中，我们可以发现A2这个结点被走过三次，如A1-A2-A4-A5-…，这样就可以算一次遍历。但是，我们如果说遍历是A4-A2-A5-A1-A6-A3…，实际上也没有任何毛病。同样地，A4-A5-A2-A6-A3-A1…也是可以的。

也就是说，如果是先访问根节点，然后先序遍历左子树，最后遍历右子树，则称为先序遍历；如果是先遍历左子树，然后访问根节点，最后遍历右子树则称为中序遍历；如果是先遍历左子树然后遍历右子树，最后遍历根节点则称为后序遍历。

我们也可以换一种思考方式。如果一个结点第一次走过时就遍历它，那么就是先序遍历，如果走过第二次再遍历则称中序遍历，如果走过第三次才遍历则称后序遍历。

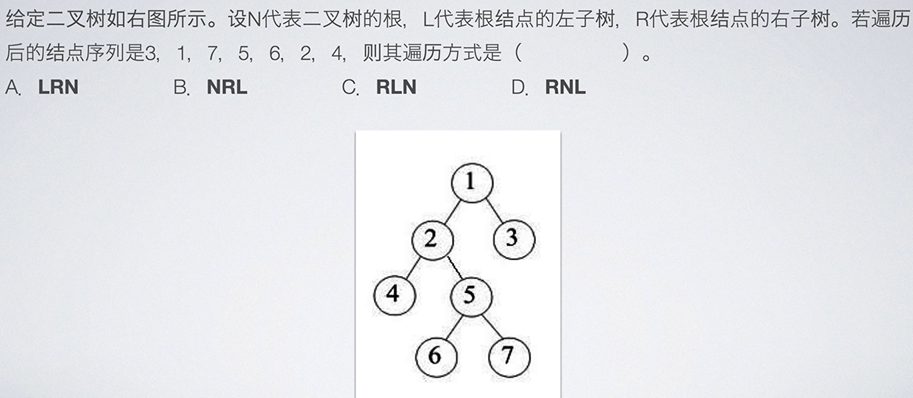
408科目09年03题

答案明显是D。这里就不多解释了。

树的层次遍历和二叉树的差不多，有差别的是深度优先遍历。如下所示：

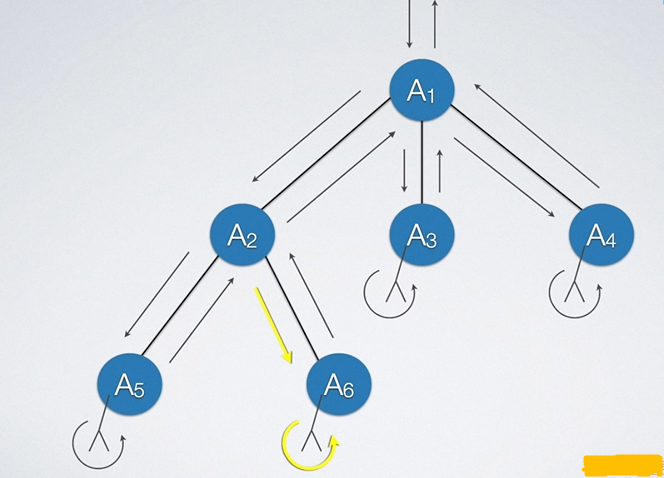
在树的遍历中，每个节点就不一定是经过三次了，故相对于前面的三种深度优先遍历方式，这里只有两种，即先序遍历和后序遍历。

我们前面说过树可以转换为二叉树。树的先序遍历和转换后的二叉树先序遍历是一样的，而树的后序遍历和转换后的二叉树的中序遍历是一样的。

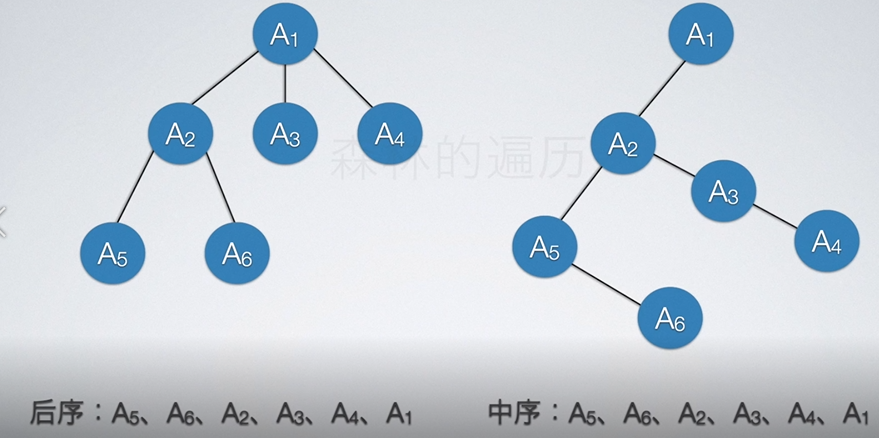
对于森林的遍历也很简单，先序遍历指的就是从左到右对每一棵树进行先序遍历；而后序遍历指的就是从左到右对每一棵树进行后序遍历。

同样的，如果将森林转为二叉树，其遍历的改变和树的改变是一样的。即森林的先序等效于转换后二叉树的先序，森林的后序等效于二叉树的中序。

文章来源: blog.csdn.net，作者：ArimaMisaki，版权归原作者所有，如需转载，请联系作者。

原文链接：blog.csdn.net/chengyuhaomei520/article/details/124698739