数据结构杂谈(九)——二叉树的遍历
9 二叉树的遍历
9.1 递归函数基础
什么是递归?调用自身就是叫递归,如下所示:
void r(){
r();
}
- 1
- 2
- 3
我们习惯借用阶梯图来帮助我们理解这些知识。如果是同一层函数体,那么习惯上在同一层阶梯中,如下所示:
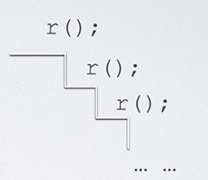
如果是像上述的方式一样来写递归函数,我们不难发现这个循环是无限的。故我们需要加一个终止条件,一般来说,我们习惯将终止条件写于函数体的最开头,当符合终止条件时,函数遍不会继续执行,如下所示:
int i = 0;
void r()
{
if(i<3)
{
++i;
r();
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
当同一层阶梯中有多个执行语句,我们习惯用一个结点来表示它执行的效果,如下所示:
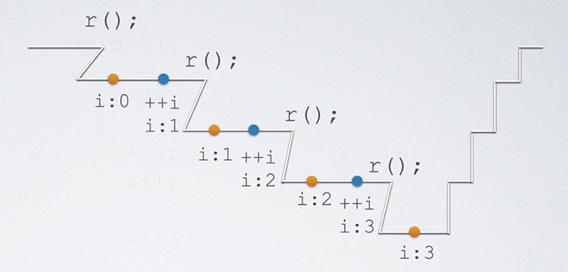
多个递归
在考研中一般不考查一个递归,而是喜好考查多个递归,在这里给出代码示例和阶梯图,望仔细研究。
int i = 0; void r() { if(i<2) { ++i; r(); r(); } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
9.2 深度优先遍历的实现
递归遍历
通过上面递归的学习,我想我们可以看穿下面这个恐怖的遍历代码了。
void r(BTNode p)
{
if(p != nullptr)
{
//(1)
r(p->lChild);
//(2)
r(p->rChild);
//(3)
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
对于一下这颗树来说:
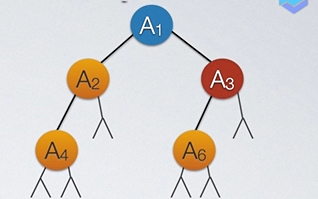
结合上述代码的遍历方式,我们可以画出如下的阶梯图。
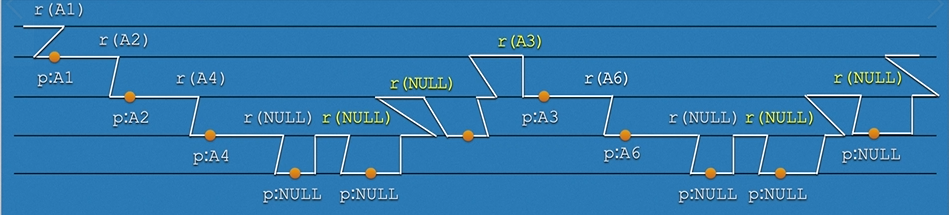
如果想要先序遍历,结合上一讲我们讲过的原理,可知遍历方式的不同在于经过第几次时去访问该元素。如果在经过第一次时就拿出结点中的元素则为先序遍历,其他遍历懂得都懂,这里不过多赘述,不清楚的可以看看上一讲。
如果想要在代码中使用先序遍历,只需要在前面的框架中将(1)替换为visit§,其中visit()这个函数可以是自己写的访问结点元素的一个函数。
void r(BTNode p)
{
if(p != NULL)
{
visit(p)
r(p->rChild);
//(2)
r(p->lChild);
//(3)
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
如果是中序则将visit()放在(2),后序则放在(3)。
先序遍历非递归
我们在栈那一讲中知道,栈的作用和递归一样。故如果不想使用递归来解决遍历的话,可以考虑用栈来解决这个问题。
入栈完读取数据后就可以出栈。左右孩子入栈时遵循先右后左,这是因为栈是后入先出,只有先右后左出栈时才能先左后右。如下:
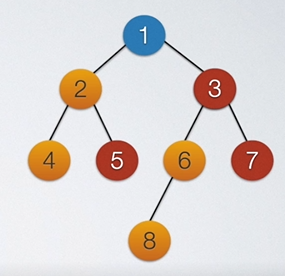
我们定义一个栈。则出入栈顺序应该是:
1入栈,1读取数据发现两个孩子结点,1出栈,先右后左,则3进栈后2进栈,而后读2,发现有孩子,故2出栈,5入栈后4入栈,读取4,发现4没有孩子,4出栈,而后5在栈顶,读取5,5没有孩子,5出栈,而后是3,读取3其有孩子,3出栈,7入栈后6入栈,读取6有孩子,6出栈,8入栈,8读取后没有孩子,8出栈,栈顶为7,读取7其无孩子,7出栈。至此先序遍历结束。
我们来看看代码的实现:
void preorderNonrecursion(BTNode *bt)
{
if(bt! = NULL)
{
BTNode * Stack[maxSize];//定义顺序栈
int top = -1;//定义栈顶指针
BTNode *p = NULL;//定义遍历指针
Stack[++top] = bt;//根节点入栈
while(top != -1)
{
p = Stack[top--];
Visit(p);//取元素
if(p->rChild != NULL)
Stack[++top] = p->rChild;
if(p->lChild != NULL)
Stack[++top] = p->lChild;
}
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
后序遍历非递归
先将后序遍历的原因是,后序遍历和先序遍历有一些关系。
我们将后序遍历的倒排叫做逆后序。如下图所示:

仔细观察逆后序我们可以发现一件事。先序遍历是先遍历根,然后遍历左子树,然后遍历右子树。而逆后序是先遍历根,然后右子树,最后左子树。
得到逆序后后,我们可以使用C++容器特有resort方法,也可以将得到的元素全部压入栈中然后取出,即可得到后序遍历。
void postorderNonrecursion(BTNode *bt)
{
if(bt! = NULL)
{
BTNode * Stack1[maxSize],*Stack2[maxSize];//定义顺序栈
int top1,top2 = -1;//定义栈顶指针
BTNode *p = NULL;//定义遍历指针
Stack1[++top1] = bt;//根节点入栈
while(top1 != -1)
{
p = Stack1[top1--];
Stack2[++top2] = p;
if(p->lChild != NULL)
Stack1[++top] = p->lChild;
if(p->rChild != NULL)
Stack1[++top] = p->rChild;
}
while(top != -1)
{
p = Stack2[top2--];
Visit(p);
}
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
中序遍历非递归化
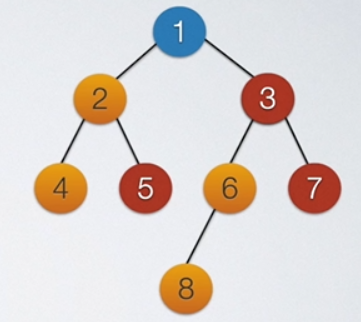
中序遍历是这么做的:开始直接一直往左的深处走,途中经过的结点全部压入栈,如上图,压入栈的有1,2,4。
而后,出栈并读取栈顶元素。若栈顶元素子树元素非空则入栈,则4出栈,栈顶元素为2。2读取元素并出栈,2有子树,故5入栈,栈中元素为1,5。
5读取元素并出栈,无子树。
1读取元素并出栈,有子树,3入栈。3有左子树,故一直往左子树深处走。途经6,8,故6,8入栈。此时栈中元素3,6,8,栈顶元素为8。
8读取元素并出栈,无子树。
6读取元素并出栈,无子树。
3读取元素并出栈,有子树,故7入栈。
7读取元素并出栈,无子树。
故全程中序遍历元素为:4,2,5,1,8,6,3,7
void inorderNonrecursion(BTNode *bt)
{
if(bt! = NULL)
{
BTNode * Stack[maxSize];//定义顺序栈
int top = -1;//定义栈顶指针
BTNode *p = NULL;//定义遍历指针
p = bt;//将遍历指针指向根节点
while(top != -1 || p!= nullptr)
{
while(p != nullptr)
{
Stack[++top] = p;
p = p->lChild;
}
if(top != -1)
{
p = Stack[top--];
Visit(p);
p = p->rChild;
}
}
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
9.3 二叉树层次遍历
想要层次遍历二叉树,我们需要辅助队列。
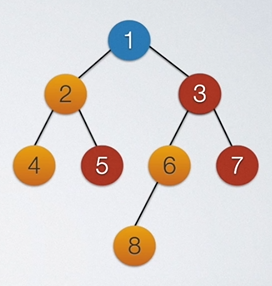
首先是1入队,然后1出队,访问1的左右子树。存在2和3。
2入队后3入队,然后2出队,访问2的左右子树。存在。故4,5入队。
3出队,访问3的左右子树,存在。故6,7入队。
4出队,访问4的左右子树,不存在。
5出队,访问5的左右子树,不存在。
6出队,访问6的左右子树,存在8,8入队。
7出队,访问7的左右子树,不存在。
8出队,访问8的左右子树,不存在。
至此遍历完成。
void level(BTNode * bt)
{
if(bt != NULL)
{
int front,rear;
BTNode *que[maxSize];
front = rear = 0;
BTNode *p;
rear = (rear +1)%maxSize;
que[rear] = bt;
while(front != rear)
{
front = (front + 1) % maxSize;
p = que[front];
Visit(p);
if(p->lChild != NULL)
{
rear = (rear + 1)%maxSize;
que[rear] = p->lChild;
}
if(p->rChild != NULL)
{
rear = (rear + 1)%maxSize;
que[rear] = p->rChild;
}
}
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
文章来源: blog.csdn.net,作者:ArimaMisaki,版权归原作者所有,如需转载,请联系作者。
原文链接:blog.csdn.net/chengyuhaomei520/article/details/125118799
- 点赞
- 收藏
- 关注作者

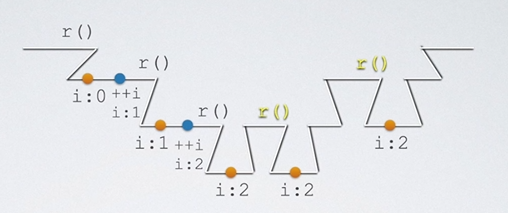

评论(0)