高斯滤波

二维情况下的高斯滤波分布
1 2 π σ x σ y exp ⁡ − ( x − u ) 2 + ( y − v ) 2 2 σ x σ y \frac{1}{2\pi \sigma_x \sigma_y} \exp { -\frac{(x-u)^2 + (y-v)^2}{2\sigma_x \sigma_y} } 2πσx​σy​1​exp−2σx​σy​(x−u)2+(y−v)2​
不过一般情况下都是让$x$方向和$y$方向的方差相等
1 2 π σ 2 exp ⁡ − ( x − u ) 2 + ( y − v ) 2 2 σ 2 \frac{1}{2\pi \sigma^2} \exp { -\frac{(x-u)^2 + (y-v)^2}{2\sigma^2} } 2πσ21​exp−2σ2(x−u)2+(y−v)2​

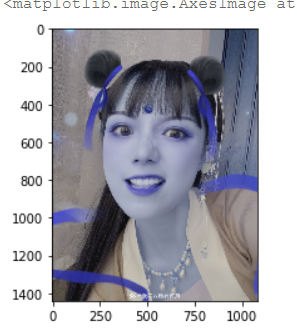
先看原图

plt.imshow(img_d1)

这个颜色是因为opencv的默认格式为BGR

在opencv里调用API如下

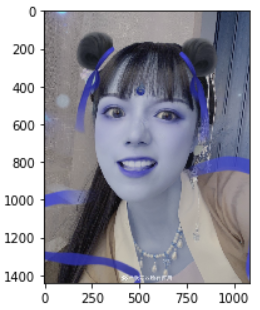
# 这里设置方差都为0.8，你也可以让两个方向的方差不等
plt.imshow(cv.GaussianBlur(img_d1_copy, (5,5), 0.8))

原理代码

# Gaussian filter
def gaussian_filter_zp(img, K_size=5, sigma=0.8):
	if len(img.shape) == 3:
		H, W, C = img.shape
	else:
		img = np.expand_dims(img, axis=-1)
		H, W, C = img.shape

		
	## Zero padding
	pad = K_size // 2
	print(pad)
	out = np.zeros((H + pad * 2, W + pad * 2, C), dtype=np.float)
	out[pad: pad + H, pad: pad + W] = img.copy().astype(np.float)

	## prepare Kernel
	K = np.zeros((K_size, K_size), dtype=np.float)
	for x in range(-pad, -pad + K_size):
		for y in range(-pad, -pad + K_size):
			K[x + pad, y + pad] = np.exp( -(x ** 2 + y ** 2) / (2 * (sigma ** 2)))
	K /= (sigma * 2 * np.pi)
	K /= K.sum()
	
	print(K)

	tmp = out.copy()
	# filtering
	for y in range(H):
		for x in range(W):
		    for c in range(C):
		        out[pad + y, pad + x, c] = np.sum(K * tmp[y: y + K_size, x: x + K_size, c])

	out = out[pad: pad + H, pad: pad + W].astype(np.uint8)

	return out

上诉代码分两部分，第一部分是根据给定的K_size和方差计算内核
K_size=5, sigma=0.8情况下的内核为

[[0.00048091 0.00501119 0.01094545 0.00501119 0.00048091]
 [0.00501119 0.0522178  0.11405416 0.0522178  0.00501119]
 [0.01094545 0.11405416 0.2491172  0.11405416 0.01094545]
 [0.00501119 0.0522178  0.11405416 0.0522178  0.00501119]
 [0.00048091 0.00501119 0.01094545 0.00501119 0.00048091]]

第二部分是一个卷积的操作，应该叫相关，相关操作之前先把图像翻转 18 0 o 180^o 180o就是卷积了
如果你嫌麻烦，opencv有卷积的API

# 这个K就是上面计算出来的高斯核
Gaussian_k = K.copy()
plt.imshow(cv.filter2D(img_d1_copy, -1, Gaussian_k))

执行代码

plt.subplot(131),plt.imshow(img_d1_copy),plt.title('Original')
plt.xticks([]), plt.yticks([])
plt.subplot(132),plt.imshow(cv.GaussianBlur(img_d1_copy, (3,3), 1, 1)),plt.title('Gaussian_opencv')
plt.xticks([]), plt.yticks([])
plt.subplot(133), plt.imshow(gaussian_filter_zp(img_d1_copy)),plt.title('gaussian_filter_zp')
plt.xticks([]), plt.yticks([])

中值滤波

中值滤波和均值滤波都很简单

原理

在图像上给出一个核的大小，计算一个核内的全部像素值，然后把核中心的像素替换为整个核内像素的中值。
在均值滤波和高斯滤波中，计算出来新的像素值可能不属于原始图像，但是中值滤波使用的就是原始图像的像素作为新的像素值。中值滤波可以很好的去除椒盐噪声。

Opencv_API

plt.imshow(cv.medianBlur(img_d1_copy, 5))

Code

def median_filter_zp(img :np.ndarray, K_size=5):
    H,W,C = img.shape
    
    pad = K_size // 2
    out = np.zeros((H+pad*2, W+pad*2, C), dtype=np.float)
    out[pad:pad+H, pad:pad+W] = img.copy().astype(np.float)
    
    tmp = out.copy()
    
    # filter
    for y in range(H):
        for x in range(W):
            for c in range(C):
                out[pad+y, pad+x, c] = np.median(tmp[y:y+K_size, x:x+K_size, c])
                
    out = out[pad:pad+H, pad:pad+W].astype(np.uint8)
    
    return out

执行

plt.subplot(131),plt.imshow(img_d1_copy),plt.title('Original')
plt.xticks([]), plt.yticks([])
plt.subplot(132),plt.imshow(cv.medianBlur(img_d1_copy, 5)),plt.title('Median_opencv')
plt.xticks([]), plt.yticks([])
plt.subplot(133), plt.imshow(median_filter_zp(img_d1_copy)),plt.title('median_filter_zp')
plt.xticks([]), plt.yticks([])

Sobel滤波

sobel滤波器是一种高通滤波器，它能放大图像中的高频成分（边缘），同样的还有Perwitt、Scharr等内核。这些定向滤波器都会计算图像函数的一阶导数。因此在滤波器方向上像素强度变化大的区域将会得到较大的值，计算图像导数的滤波器称为高通滤波器
g r a d ( I ) = [ ∂ I ∂ x , ∂ I ∂ y ] T grad(I) = [\frac{\partial I}{\partial x}, \frac{\partial I}{\partial y}]^T grad(I)=[∂x∂I​,∂y∂I​]T

Sobel Kernel

# vertical
array([[-1., -2., -1.],
       [ 0.,  0.,  0.],
       [ 1.,  2.,  1.]])

# horizontal
array([[-1.,  0.,  1.],
       [-2.,  0.,  2.],
       [-1.,  0.,  1.]])

执行步骤和上述代码一样

def different_filter_zp(img: np.ndarray, K_size=3):
    H,W,C = img.shape
    
    # zero padding
    pad = K_size // 2
    out = np.zeros((H+pad*2, W+pad*2, C), dtype=np.float)
    out[pad:pad+H, pad:pad+W] = img.copy().astype(np.float)
    
    tmp = out.copy()
    
    out_v = out.copy()
    out_h = out.copy()
    
    # vertical kernel
    Kv = np.array([[-1., -2., -1.],[0., 0., 0.],[1., 2., 1.]])
    # Horizontal kernel
    Kh = np.array([[-1., 0., 1.],[-2., 0., 2.], [-1., 0., 1.]])
    
    print(K_size)
    # filter
    for y in range(H):
        for x in range(W):
            for c in range(C):
                out_v[y+pad, x+pad, c] = np.sum(Kv * tmp[y:y+K_size, x:x+K_size, c])
                out_h[y+pad, x+pad, c] = np.sum(Kh * tmp[y:y+K_size, x:x+K_size, c])
    out_v = np.clip(out_v, 0, 255)
    out_h = np.clip(out_h, 0, 255)
    
    out_v = out_v[pad:pad+H, pad:pad+W].astype(np.uint8)
    out_h = out_h[pad:pad+H, pad:pad+W].astype(np.uint8)
    
    return out_v, out_h

打印结果

# 执行
different_filter_zp_v, different_filter_zp_h = different_filter_zp(img_d1_RGB)
# print
plt.subplot(1,2,1)
plt.imshow(different_filter_zp_v),plt.title('v')
plt.xticks([]), plt.yticks([])
plt.subplot(1,2,2)
plt.imshow(different_filter_zp_h),plt.title('h')
plt.xticks([]), plt.yticks([])

对比调用opencvAPI

plt.subplot(1,2,1)
plt.imshow(cv.Sobel(img_d1_RGB,-1, 0,1)), plt.title('Opencv_Sobel_v')
plt.xticks([]),plt.yticks([])
plt.subplot(1,2,2)
plt.imshow(cv.Sobel(img_d1_RGB,-1, 1,0)), plt.title('Opencv_Sobel_h')
plt.xticks([]),plt.yticks([])

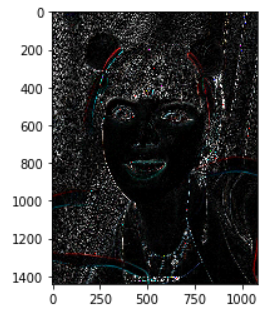
note

相同时求得水平和竖直方向的梯度，建议使用L1范数

plt.imshow(abs(different_filter_zp_v) + abs(different_filter_zp_h))

拉普拉斯（计算二阶导）

l a p l a c i a n ( I ) = ( ∂ I ∂ x ) 2 , ( ∂ I ∂ y ) 2 laplacian(I) =\sqrt{({ \frac{\partial I}{\partial x}})^2, ({\frac{\partial I}{\partial y}})^2} laplacian(I)=(∂x∂I​)2,(∂y∂I​)2 ​
与Sobel相比，拉普拉斯算子在计算时可以使用更大的内核，并且对噪声更加敏感，（因为这些更大的内核是用高斯函数的二阶导数计算的），这些算子也称为**高斯-拉普拉斯算子（Laplacian of Gaussion, LOG）**拉普拉斯算子内核的值的累加和总是0.这保证在强度值恒定的区域中，拉普拉斯算子将变为0。