Sets and Strings

Strings

Definition 2.1. An alphabet is any collection of symbols.

  
 

  
1
 

字母表是任何符号的集合

Definition 2.2. Take any alphabet Σ. A string over the alphabet Σ is
any sequence of letters in an alphabet.

  
 

  
1
  
2
 

以任何字母Σ为例。字母Σ上的字符串是字母表中的任何字母序列。

Definition 2.3. The length of any string is the number of characters
in that string.

  
 

  
1
  
2
 

任何字符串的长度都是字符的数量

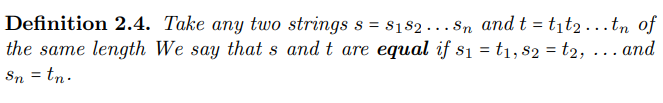
换句话说，当且仅当两个字符串字面上的字符对字符完全相同时，它们是相等的!注意，两个长度不同的字符串总是不相等的。

我们规定st是字符串s与字符串t的连接

Definition 2.6. Let s and t be strings. We say that s is a prefix of t
if t is just s with some additional stuff possibly tacked on the end: i.e. if
we can find a third string u such that su = t.

Similarly, we say that s is a suffix of t if t is just s with some additional
stuff possibly tacked on the front: i.e. if we can find a third string u such
that us = t.

Finally, we say that s is a substring (alternately, an “infix”) of t if t
is just s with some stuff possibly tacked on both the front and end: i.e.
if we can find strings u, v such that usv = t.

  
 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
 

让s和t是字符串。我们说s是t的前缀.如果t只是s最后加上一些额外的东西,我们可以找到第三个字符串u，使得su = t。

类似地，如果t只是s加上一些可能附加在前面的东西:例如，如果我们能找到第三个字符串u，使us = t。我们说s是t的后缀，

最后，如果t只是s，可能在前端和末端都附加了一些东西:如果我们能找到字符串u, v，使usv = t。我们说s是t的子串(或者说是“中缀”).

Claim 2.1. The empty string λ is a prefix, suffix, and substring of every
string t.

  
 

  
1
  
2
 

空字符串λ是每个字符串t的前缀、后缀和子字符串。

Claim 2.2. If s is a prefix of t, then s is a substring of t.

  
 

  
1
 

如果s是t的前缀，那么s是t的子串

Sets

Definition 2.7. A set A is just a collection of things. We call those
things the elements of A, and write x ∈ A to denote with symbols the
statement “x is an element of A.”

To describe a set, we just list its elements between a pair of curly braces:
for example, {1, 2, 3} would be how we would describe the set consisting
of the three numbers 1, 2 and 3.

  
 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
 

集合A就是一些东西的集合。我们
将x∈A表示为A的元素
" x是a的一个元素"

要描述一个集合，只需在一对花括号之间列出它的元素:例如，{1,2,3}是描述由数字1,2和3组成的集合的方式。

Definition 2.8. A set A has size n if it contains precisely n different
elements. If A contains infinitely many different elements, we say that
A has “infinite” size. We denote the size of A by writing ∣A∣.

  
 

  
1
  
2
  
3
 

如果它恰好包含n个不同的元素,集合A的大小为n。如果A包含无限多个不同的元素，我们说A的大小是“无限”的。我们通过写∣A∣来表示A的大小。

Definition 2.9. Take two sets A, B We say that B is a subset of A,
and write B ⊆ A, if every object in B is also an object in A.

  
 

  
1
  
2
 

取两个集合A和B，如果B中的每个对象也是A中的一个对象,我们说B是A的子集，写作B⊆A。

Definition 2.10. Let A, B be a pair of sets. We define the union of
these two sets, A ∪ B, to be the collection of all elements that are in
either A or B or both.

  
 

  
1
  
2
  
3
 

设A, B是一对集合。定义这两个集合的并集：
A∪B，是其中所有元素的集合，不是A就是B，或者两者都有。

Definition 2.11. Let A, B be a pair of sets. We define the intersection
of these two sets, A ∩ B, to be the collection of all elements that are in
both A and B at the same time.

  
 

  
1
  
2
  
3
 

设A, B是一对集合。我们定义在这两个集合中交集：
A∩B，是所有A和B中的元素同 时出现的集合。

Definition 2.12. Let A, B be a pair of sets. We define the difference
of these two sets, written A∖B or alternately A−B, to be the collection
of all elements that are both in A and not in B at the same time.

  
 

  
1
  
2
  
3
 

设A, B是一对集合。我们定义差集，写成A∖B或写成A - B，作为所有同时在A但不在B中的元素集合。

Definition 2.13. We say that two sets A, B are equal if they both
consist of the same elements; that is, if
• Every element in A is a element in B, and
• Every element in B is also a element in A.

  
 

  
1
  
2
  
3
  
4
 

我们说集合A和集合B相等，如果它们都相等
相同的:由相同的元素组成的;也就是说,如果
•A中的每个元素都是B中的一个元素，并且
•B中的每个元素在a中也是一个元素。

Claim 2.3. Let A, B be any two sets such that A ⊆ B. Then A∪B = B.

  
 

  
1
 

设A, B为A⊆B的任意两个集合，则A∪B = B

Claim 2.4. Let A, B be any two sets. Then (A ∖ B) ∖ A = ∅.

  
 

  
1
 

设A B是任意两个集合。则(A∖B)∖A =∅。

Claim 2.5. If A, B, C are three sets, then A∖(B∪C) = (A∖B)∩(A∖C).

  
 

  
1
 

如果A、B、C是三个集合，则A∖(B∪C) = (A∖B)∩(A∖C)。

文章来源: blog.csdn.net，作者：十八岁讨厌编程，版权归原作者所有，如需转载，请联系作者。

原文链接：blog.csdn.net/zyb18507175502/article/details/124232581